涡动下高速离心泵的内部流动特性研究
袁建平, 沈陈栋, 刘 君, 付燕霞, 周帮伦
(国家水泵及系统工程研究中心,江苏 镇江 212013)
涡动下高速离心泵的内部流动特性研究
袁建平, 沈陈栋, 刘君, 付燕霞, 周帮伦
(国家水泵及系统工程研究中心,江苏 镇江212013)
引起高速离心泵振动的原因很多,其中一种是由于流体作用力导致叶轮发生偏心转动,即“涡动”引起的高速离心泵的振动。为了探讨涡动情况下高速离心泵内部流场特性,以高速离心泵为研究对象,给定了三种流量、四种偏心距以及六种涡动频率比组成的不同方案,应用CFX软件对高速离心泵的内部流动进行定常数值模拟,研究了涡动频率比、偏心距对高速泵内部流动的影响。结果表明:在1.0Qd设计工况点,偏心距越小,叶片进口低压区面积越小;在0.6Qd小流量工况点,当涡动频率比小于0时,随着涡动频率比的减少,旋涡的个数逐渐增加,旋涡的面积增大;在1.7Qd大流量工况点,当涡动频率比小于0时,随着偏心距的增大,旋涡的个数增加,旋涡区面积增大;在1.0Qd设计工况点,切向力Ft受涡动频率比以及偏心距的影响很小,且随着流量的变化,它在x轴、y轴、z轴分力的方向均会发生变化。
高速离心泵;数值模拟;流场分析;流体力;涡动频率比
近年来,离心泵向着高速化、大型化、结构轻巧化的方向发展,其通用性强,使用量约占离心泵的20%。然而离心泵在高速旋转时,转子系统常常发生剧烈振动,振动会导致零件磨损,降低离心泵的效率以及使用寿命,产生噪声,严重时可能使转子失稳造成事故[1-2]。
高速离心泵的振动受很多因素影响,总结起来可以归纳为如下两部分[3-6]:一是机械方面(设计以及制造精度)的原因引起的振动,如设计不合理、装配间隙过大以及转子质量不平衡所引起的振动等;二是流体作用力引起的振动,如叶片内的不均匀液流、口环处的泄露流动和轴承内的油膜力等。转子质量不平衡所引起的振动属于强迫振动,而叶轮内流体产生的不平衡作用力引起的振动,其振动频率与转动角速度不相等,称为“涡动”[7]。
目前,国内外不少研究者[8-10]对电动机、风机、压缩机的“涡动”问题做了一定数量的理论分析。在水泵领域,曹卫东等[11]基于流固耦合对矿用潜水电泵转子系统进行优化;李同杰等[12]研究了横向流体激振力对不平衡离心叶轮的影响。虽然国内的研究者对转子动力学做了一些理论的分析,但发现对工程实际的研究分析较小。因此本文采用ANSYS CFX软件,给定了三种流量,四种偏心距以及六种涡动频率比组成的不同方案,研究了涡动比、流量和偏心距对高速泵内部流场的影响。
1计算模型与网格划分
1.1计算模型
本文选用的高速离心泵的主要设计参数如:额定流量Qd=7.5 m3/h,扬程H=85 m,转速n=7 600 r/min,比转速ns=45。模型泵叶轮部件的主要几何参数如表1所示。

表1 叶轮的主要设计参数
本文是研究涡动情况下,泵内部的流动特性。在涡动情况下,叶轮的旋转中心并不是固定不变的,而是与轴心存在一定的偏离。由于涡动运动是一个包括涡动转速ω、偏心距离ε的运动。涡动频率比是指涡动转速ω与电机拖动转速ε的比值。因此在进行数值计算时通过给定偏心距离ε和涡动转速ω,并结合电机拖动转速Ω实现高速离心泵在涡动情况下的内部流场分析。其中高速离心泵在给出偏心距和涡动速度下的计算模型如图1所示。
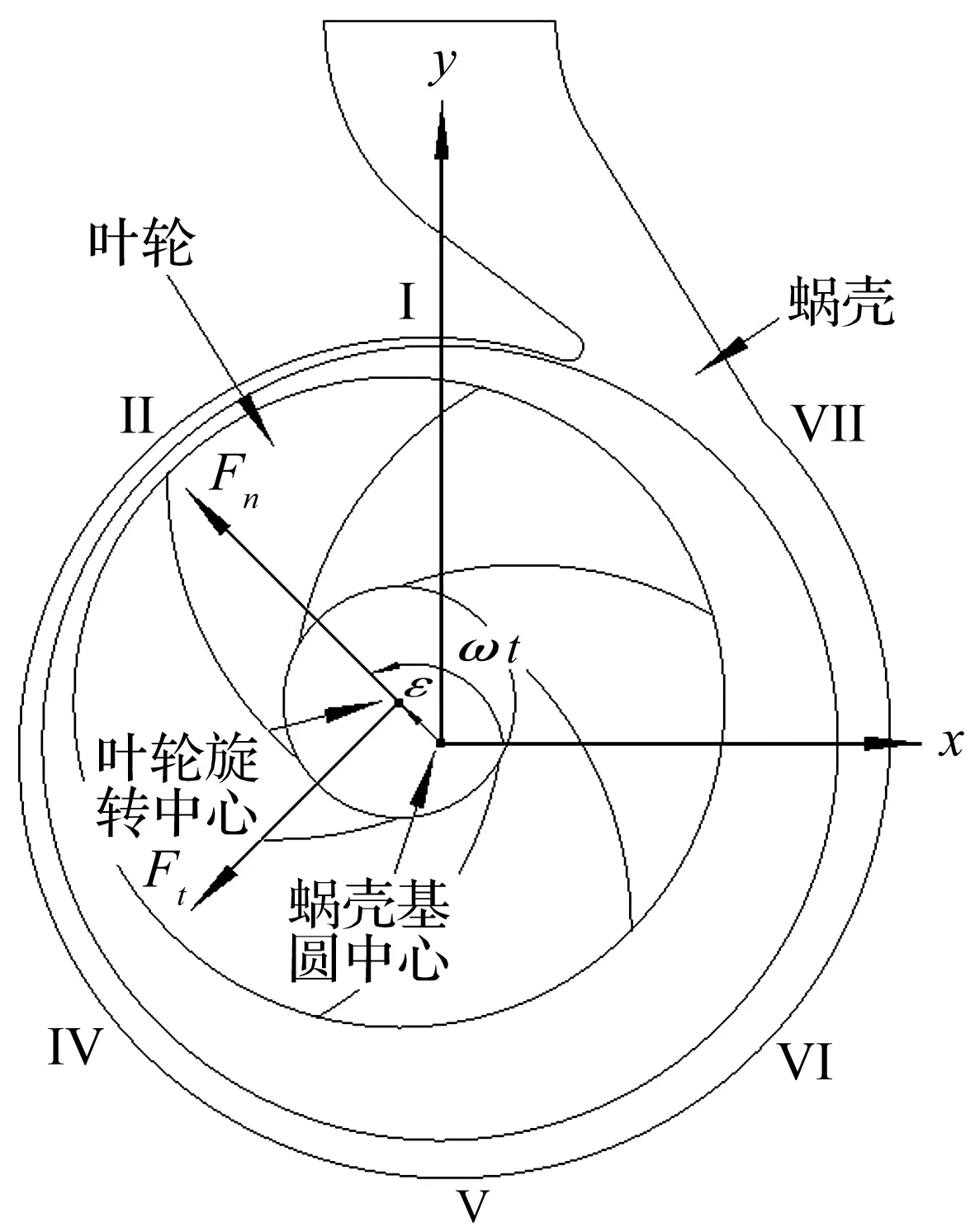
图1 高速泵涡动下的模型Fig.1 The model of the high-speed pump under whirling
为了探讨不同涡动频率比以及不同偏心距对高速离心泵内部流动特性的影响,给出四种不同的偏心距,三种流量以及六种不同涡动频率比下的设计方案,其参数如表2所示。

表2 高速离心泵涡动下的设计方案
1.2网格划分
利用ICEM软件对模型泵计算区域进行网格划分,采用具有较强适应性的四面体网格,所选用的网格总数为425万,如图2所示。
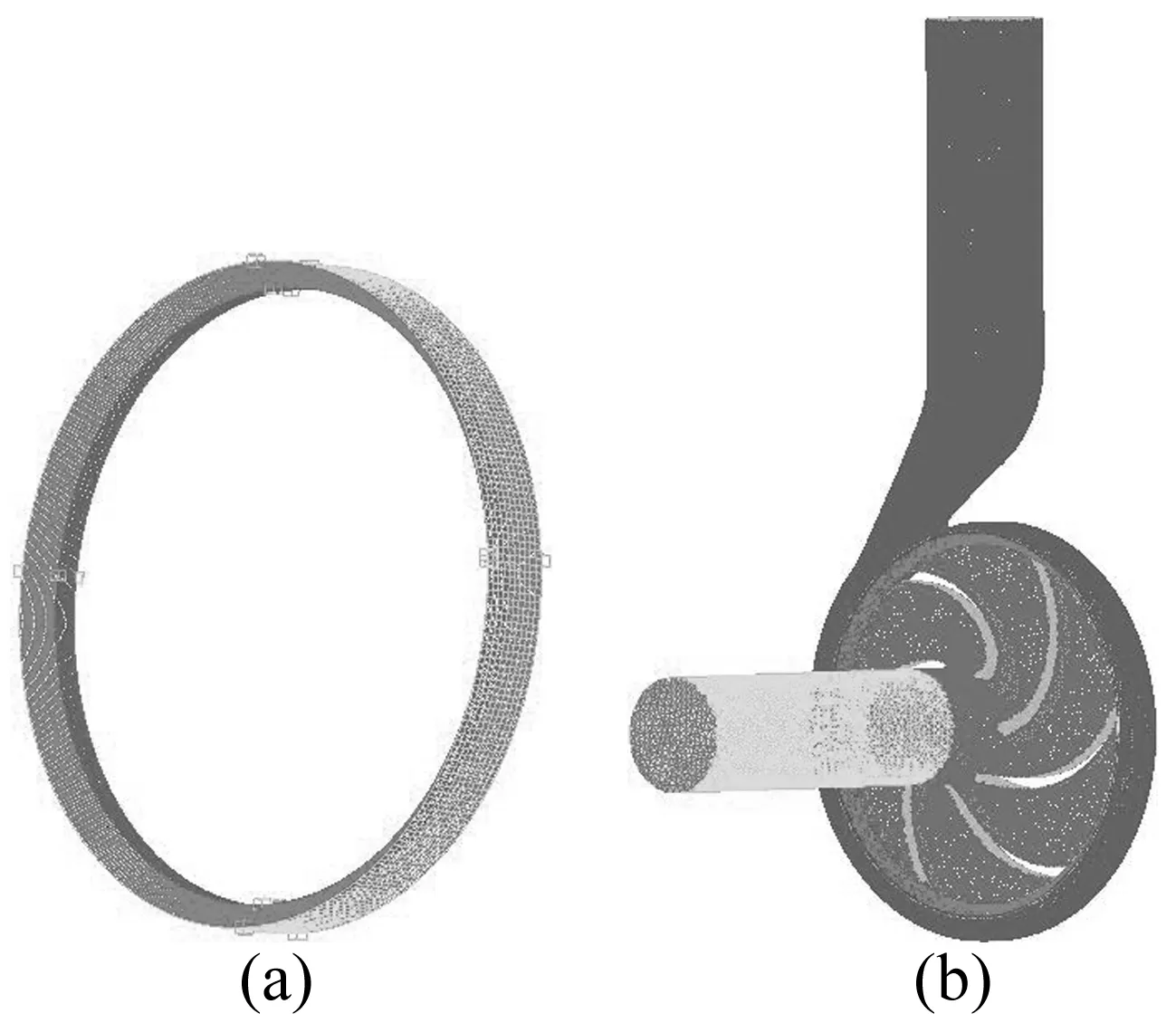
图2 模型泵计算区域网格划分Fig.2 The meshing of the computational domain ofthe model pump

计算域进口叶轮间隙蜗壳网格数150436383895171568192125
2数值模拟方法
2.1湍流模型
RNGk-ε模型计算流场较精确,而且可以通过修正湍动黏度来更好的处理高应变率及流线弯曲程度较大的旋转流动情况。因此本文采用RNGk-ε湍流模型,k方程和ε方程如下。
(1)
(2)
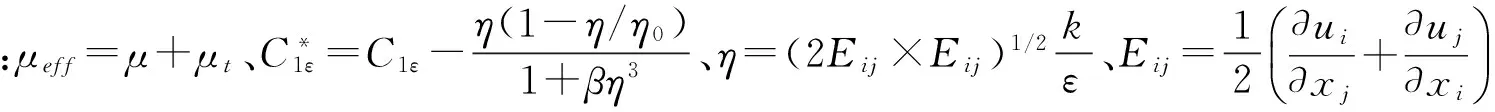
上述湍流模型中的参数选择如下:η0=4.377、Cμ=0.084 5、αk=αε=1.39、C1ε=1.42、C2ε=1.68、β=0.012
2.2边界条件
计算时叶轮区域采用旋转坐标系,进口采用速度进口,出口为自由出流;壁面选择无滑移壁面;近壁区采用标准壁面函数。残差收敛精度设置为10-4。
3结果分析
3.1涡动下高速泵内部的静压分布
为了研究涡动频率比、偏心距对高速离心泵内部静压分布的影响。以偏心距0.3 mm为例,研究了1.0Qd设计工况时六种涡动频率比、三种不同偏心距的静压分布,结果如图3~图4所示。
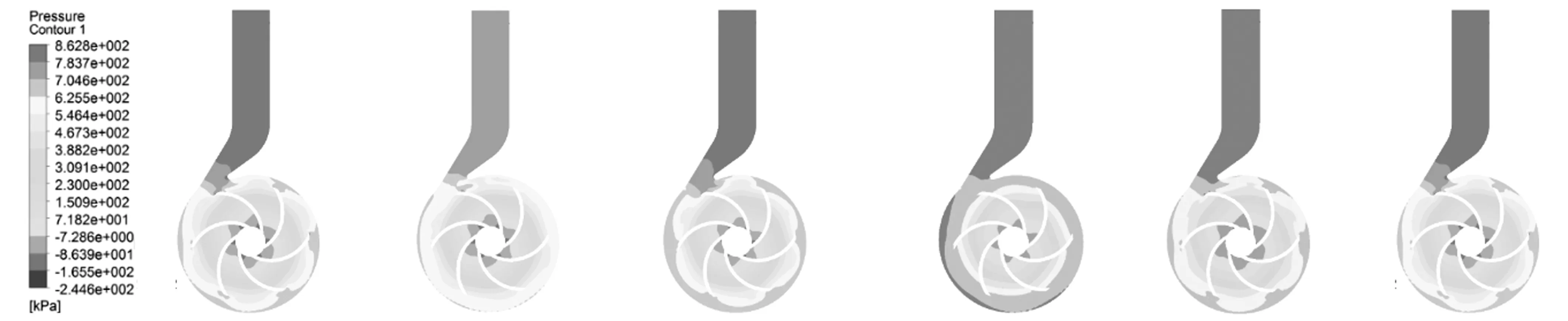
(a) ω/Ω=-0.4 (b) ω/Ω=-0.2 (c) ω/Ω=-0.1 (d) ω/Ω=0.1 (e) ω/Ω=0.2 (f) ω/Ω=0.4图3 1.0Qd高速离心泵中间截面静压分布Fig.3 The static pressure distribution in the middle span of the high-speed centrifugal pump at 1.0Qd
图3为1.0Qd设计流量工况点六种不同涡动频率比的静压分布。从图3中可以看出,在1.0Qd设计流量工况点,涡动频率比ω/Ω的变化对叶轮流道内的低压区域面积以及压力梯度影响不大。图4为设计工况点下ω/Ω=0.2时的静压分布,从图4中可以看出,在1.0Qd设计流量工况点,随着偏心距的增大,叶轮进口低压区面积逐渐增大,蜗壳流道内的压力分布也变得不均匀。
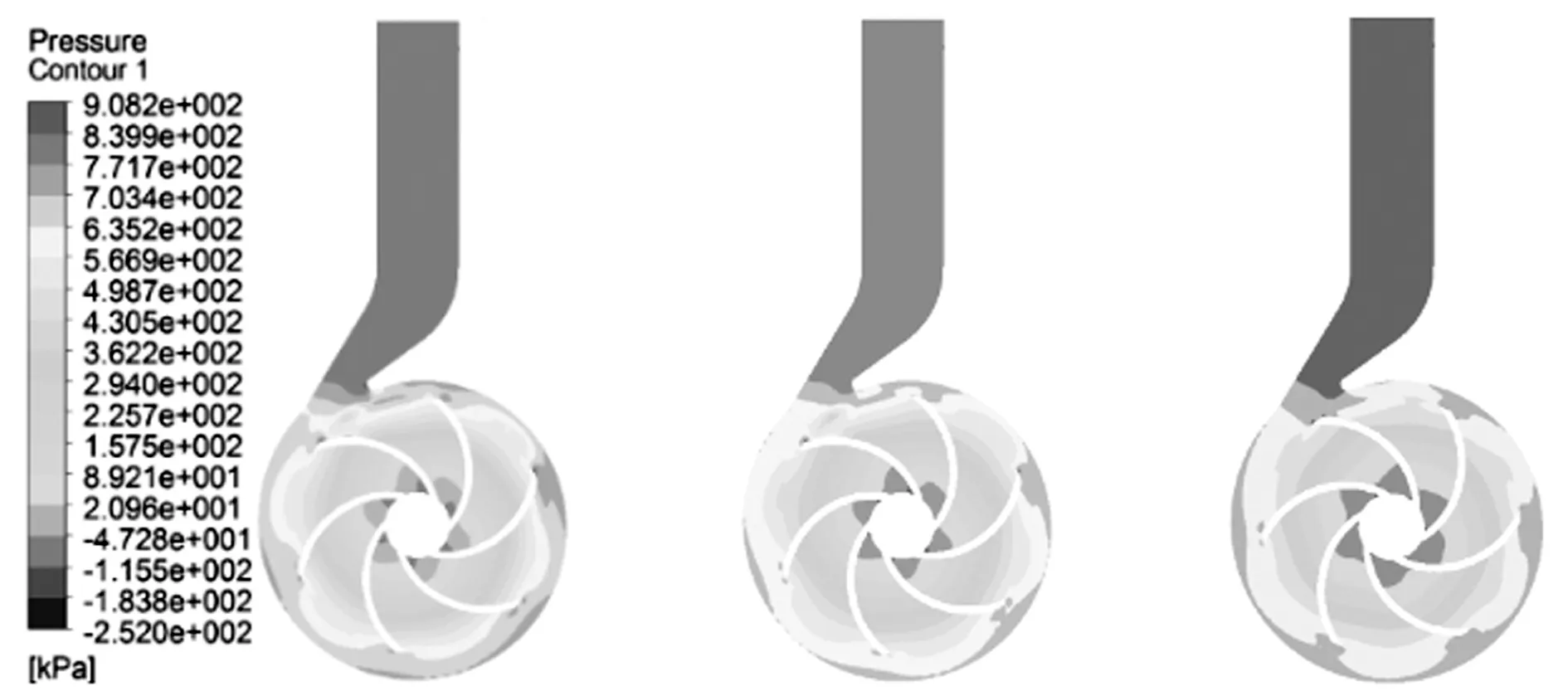
(a) ε=0.1 mm (b) ε=0.2 mm (c) ε=0.3 mm图4 1.0Qd高速离心泵三种不同偏心距下中间截面静压分布Fig.4 The static pressure distribution in the middle span at 1.0Qd under three different eccentricity
3.2涡动下高速离心泵速度流线分布
涡动下高速离心泵的叶轮不但具有电机的拖动转速还具有绕自身轴心转动的涡动速度,因此其内部流动更为复杂。为了研究不同涡动频率比对高速泵内部流动的影响,以偏心距0.3 mm的情况为例,分析了三种流量、六种涡动频率比下高速离心泵中间截面的速度流线分布,如图5~图7所示。
从图5~图7中可以看出,在0.6Qd工况点,当ω/Ω<0时,随着涡动频率比的减少,旋涡的个数逐渐增加,旋涡的面积增大。在1.0Qd工况点,在ω/Ω=-0.2以及ω/Ω=0.4时,高速泵中间截面流道的流线分布较为均匀,旋涡个数最少。在1.7Qd工况点,涡动频率比对旋涡个数的影响不大。
图8为1.7Qd工况下两种涡动比、三种偏心距下的速度流线图,从图中可以看出在ω/Ω<0时,随着偏心距的增大旋涡的个数增加,旋涡区面积增大,动能耗散增加。说明此时偏心距对于高速泵的内部流动有一定的影响。在ω/Ω>0时,偏心距的增大对于叶轮流道内旋涡的变化影响不明显,但对隔舌处的流动影响较大,隔舌处出现一个较大的低压区,低压区流体速度主要集中在3.445 m/s以下。

(a) ω/Ω=-0.4 (b) ω/Ω=-0.2 (c) ω/Ω=-0.1 (d) ω/Ω=0.1 (e) ω/Ω=0.2 (f) ω/Ω=0.4图5 0.6Qd高速离心泵中间截面相对速度流线分布Fig.5 The relative velocity distribution in the mid span of the high-speed centrifugal pump at 0.6Qd
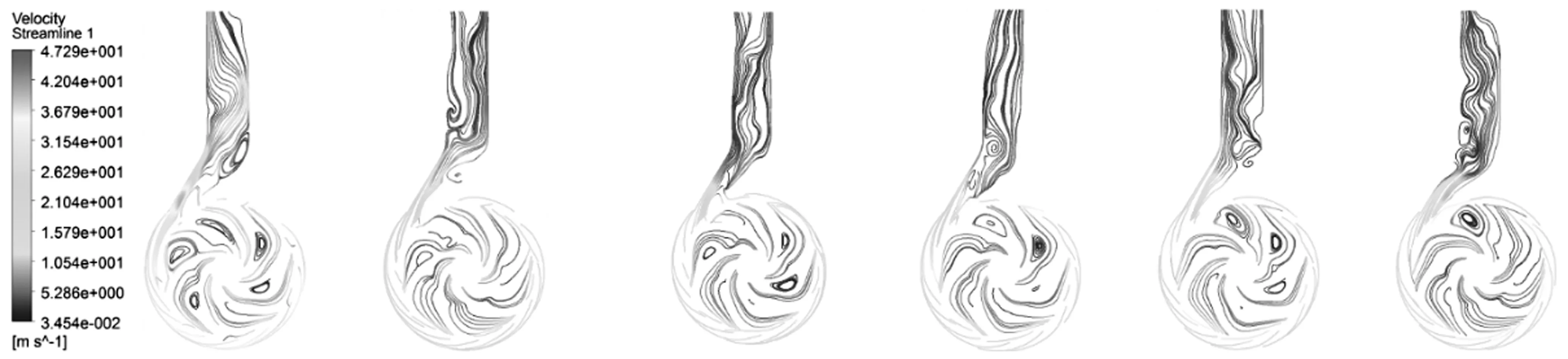
(a) ω/Ω=-0.4 (b) ω/Ω=-0.2 (c) ω/Ω=-0.1 (d) ω/Ω=0.1 (e) ω/Ω=0.2 (f) ω/Ω=0.4图6 1.0Qd高速离心泵中间截面速度流线分布Fig.6 The relative velocity distribution in the mid span of the high-speed centrifugal pump at 1.0Qd

(a) ω/Ω=-0.4 (b) ω/Ω=-0.2 (c) ω/Ω=-0.1 (d) ω/Ω=0.1 (e) ω/Ω=0.2 (f) ω/Ω=0.4图7 1.7Qd高速离心泵中间截面相对速度流线分布Fig.7 The relative velocity distribution in the mid span of the high-speed centrifugal pump at 1.7Qd

(a) ε=0.1 mm (b) ε=0.2 mm (c) ε=0.3 mm (a) ε=0.1 mm (b) ε=0.2 mm (c) ε=0.3 mm图8 ω/Ω=-0.2和ω/Ω=0.2时的速度流线分布图Fig.8 Speed streamline distribution at ω/Ω=-0.2 and ω/Ω=0.2
3.3不同偏心距下高速离心泵切向力特性分析
高速离心泵在运行过程中会产生多种作用力,其中主要包括轴承处的油膜力,密封处的压力以及叶轮内部流动和泄漏流动产生的流体作用力。然而在研究内部流场力时,绝大部分力来自叶轮受到的流体力。由于切向分力Ft和法向分力Fn的存在,使得叶轮发生涡动。与轴承和高速离心泵泵体能够产生的潜在反作用力(回复力)相比法向分力Fn小很多,由计算结果法向分力Fn数值主要集中在-2N~2N之间,对于高速泵的涡动稳定性影响很小。因此本文研究流量、涡动频率比以及偏心距等因素与切向分力Ft之间的关系,如图9~图11所示。
图9为切向力Ft在x方向分力的分布图。从图中可以看出,随着流量的增大切向力Ft在x方向的分力先减小再增大,由负值变为正值。在1.0Qd工况下,Ftx的数值相对较小,且涡动频率比以及偏心距的变化对于Ftx基本无影响,主要集中在-1.2~-0.4 N之间。在1.7Qd大流量工况下,Ftx在偏心距ε=0.1 mm和ε=0.2 mm时受涡动频率比的影响很小,主要集中于28~40 N之间。在偏心距ε=0.3 mm时,随着ω/Ω的增大Ftx逐渐增大。
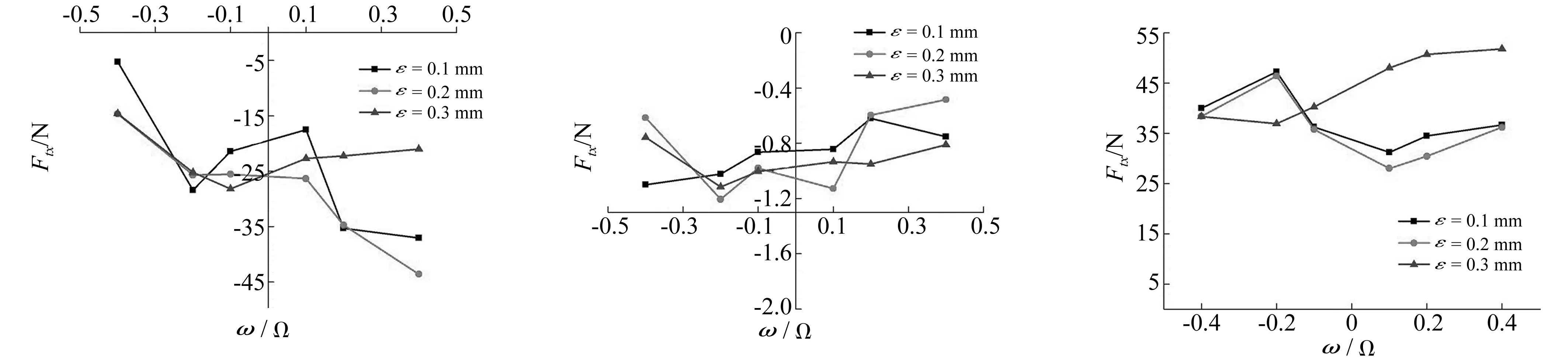
(a) 0.6Qd(b) 1.0Qd(c) 1.7Qd图9 不同偏心距下切向力Ft在x方向分力的分布曲线Fig.9CurvedistributionoftangentialforceFtinx-directionunderdifferenteccentricity

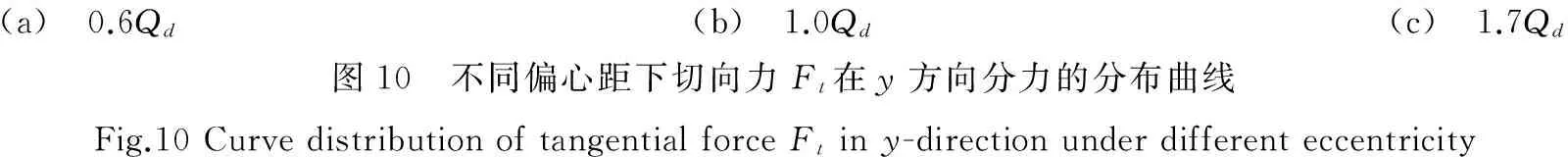
(a) 0.6Qd(b) 1.0Qd(c) 1.7Qd图10 不同偏心距下切向力Ft在y方向分力的分布曲线Fig.10CurvedistributionoftangentialforceFtiny-directionunderdifferenteccentricity


(a) 0.6Qd(b) 1.0Qd(c) 1.7Qd图11 不同偏心距下切向力Ft在z方向分力的分布曲线Fig.11CurvedistributionoftangentialforceFtinz-directionunderdifferenteccentricity
图10为切向力Ft在y方向分力的分布图。从中可以发现随着流量的增大Fty先减小后增大,由正值降为负值。在1.0Qd工况点,Fty的变化很小基本维持在0~-1 N之间。说明在设计工况点,涡动频率比以及偏心距的变化对叶轮的受力影响很小。在1.7Qd大流量工况下,当ω/Ω<0时随着涡动频率比的增加Fty逐渐变大,且随着偏心距的增大Fty逐渐变大。Fty和ω/Ω之间满足二次函数关系,可采用二次多项式进行拟合。从图中可以发现,曲线开口方向向上。当偏心距为0.1 mm、0.2 mm和0.3 mm时,其回归决定系数R2分别为0.791 1、0.919 5和0.955 5。
从图11中可以得出,随着流量的增大切向力Ftz先减小再增大,由负值逐渐变为正值。在0.6Qd小流量工况下,随着涡动频率比的增大Ftz逐渐降低。且在偏心距ε=0.2 mm时,Ftz下降幅度最大,说明偏心距对Ftz的变化影响较大。在设计工况下时,Ftz较小,主要集中在-0.4 N~-0.1 N之间。同样的在1.0Qd设计工况点附近时,涡动频率比和偏心距对切向力Ftz的影响很小。在1.7Qd大流量工况下,当ω/Ω<0时随着涡动比的增加三种偏心距下的切向力Ftz逐渐变小,其中在偏心距ε=0.3 mm时,Ftz下降最快。且Ftz和ω/Ω之间满足二次函数关系,可进行二次多项式拟合。此时曲线开口向上,当偏心距为0.1 mm、0.2 mm和0.3 mm时,其回归决定系数R2分别为0.984 1、0.950 8和0.971 2。
4结论
(1) 在1.0Qd设计流量工况点,随着偏心距的增大,叶轮进口低压区面积逐渐增大。涡动频率比对低压区面积的影响不大。
(2) 在0.6Qd小流量工况点,当ω/Ω<0时,随着涡动频率比的减少,旋涡的个数逐渐增加,旋涡的面积增大。
(3) 在1.7Qd小流量工况点,当ω/Ω<0时,随着偏心距的增大旋涡的个数增加,旋涡区面积增大,动能耗散增加。
(4) 高速离心泵内部的涡动特性主要受切向力Ft的影响。在1.0Qd设计工况下,涡动比以及偏心距对切向力Ft的影响很小。在1.7Qd大流量工况下,Ft和ω/Ω之间满足一定的二次函数关系,可采用二次多项式进行拟合。
[ 1 ] 陈林华.不对中转子系统振动特征分析与诊断[J].压缩机技术,2003,10(6):16-18.
CHEN Lin-hua.Analysis and diagnosis to the vibration characteristic of non-concentric rotor system[J].Compressor Technology,2003,10(6):16-18.
[ 2 ] Fu Yan-xia,Yuan Jian-ping,Yuan Shou-qi,et al.Numerical and experimental analysis of flow phenomena in a centrifugal pump operating under low flow rates[J].ASME J.Fluids Eng,2014,137(1):1-12 .
[ 3 ] 徐龙祥.高速旋转轴系动力学设计[M].北京:国防工业出版社,1994:72.
[ 4 ] KauPert K A,Staubli T.The unsteady pressure field in a high specific speed centrifugal Pump impeller-partⅠ:influence of the volute[J].ASME J.Fluids Eng,1999,121(9):621-626.
[ 5 ] KauPert K A,Staubli T.The unsteady pressure field in a high specific speed centrifugal Pump impeller-partⅡ:influence of the volute[J].ASME J.Fluids Eng,1999,121(9):627-632.
[ 6 ] 张德胜,汪靖,施卫东,等.高压多级离心泵转子系统的不平衡相应特性[J].排灌机械工程学报,2014,32(1):17-22.
ZHANG De-sheng,WANG Jing,SHI Wei-dong,et al.Unbalance response characteristics of rotor system in high pressure multi-stage pump[J].Drainage and Irrigation Machinery,2014,32(1):17-22.
[ 7 ] Vance J M.Rotor dynamics of turbomachinery[M].New York:John Wiley and Sons,1988.
[ 8 ] 杨永锋,任兴民,徐斌.国外转子动力学研究综述[J].机械科学与技术,2011,30(10):1775-1781.
YANG Yong-fen,REN Xing-min,XU Bin.Review of international research on rotor dynamics[J].Mechanical Science and Technology for Aerospace Engineering,2011,30(10):1775-1781.
[ 9 ] 缪红燕,高金吉,徐鸿.转子系统瞬态不平衡响应的有限元分析[J].振动与冲击,2004,23(3):1-5.
MIAO Hong-yan,GAO Jin-ji,XU Hong.Transient response of unbalanced rotor system through its critical speed[J].Journal of Vibration and Shock,2004,23 (3) :1-5.
[10] Chew C S, Yeo K S,Shu C.A generalized finite difference(GFD) ALE scheme for incompressible flows around moving solid bodies on hybrid meshfrss Cartesian grids[J].Journal of Computational Physics,2006,218(2):510-548.
[11] 曹卫东,高一,王秀兰,等.基于Ansys的矿用潜水电泵转子系统的优化设计[J].排灌机械工程学报,2012,30(2):157-163.
CAO Wei-dong,GAO Yi,WANG Xiu-lan,et al.Optization design of submersible pump rotor system for coal mine mine base on Ansys[J].Drainage and Irrigation Machinery,2012,30(2):157-163.
[12] 李同杰,孙启国,王娟.横向流体激振力作用下的不平衡离心叶轮转子分岔特性研究[J].振动与冲击, 2007,26(4):144-146.
LI Tong-jie,SUN Qi-guo,WANG Juan.Study on the unbalanced centrifugal impeller rotor under lateral fluid force[J].Journal of Vibration and Shock,2007,26(4):144-146.
Internal flow characteristic of high-speed centrifugal pumps under whirling of their imp
YUAN Jian-ping, SHEN Chen-dong, LIU Jun, FU Yan-xia, ZHOU Bang-lun
(National Research Center of Pumps, Zhenjiang 212013, China)
In many factors causing vibration of high-speed centrifugal pumps, one is the whirling motion of their impellers under the action of fluid force. In order to investigate their internal flow, a high-speed centrifugal pump’s internal flow field was simulated based on the study schemes consisting of three different flow rates, four different eccentricities and six different whirl frequency ratios by using the commercial software CFX. In addition, the effects of whirl frequency ratio, flow rate and eccentricity on the internal flow field of the high-speed pump were also studied. The results showed that the low pressure area in the inlet of the impeller is the minimum at the design point while eccentricity is close to zero; under the condition of lower flowrate, the number of vortex increases with decrease in whirl frequency ratio when whirl frequency ratio is negative; under the condition of higher flowrate, the number of vortex increases with increase in eccentricity when whirl frequency ratio is negative; the tangential forceFtis weakly dependent on eccentricity and whirl frequency ratio, its components inx-axis,y-axis andz-axis change with variation of flow rate.
high-speed centrifugal pump; numerical analysis; flow field analysis; fluid force; whirl frequency ratio
10.13465/j.cnki.jvs.2016.11.014
国家自然科学基金(51409125);中国博士后科学基金(2014M551515;2015T80507);江苏省高校自然科学基金(14KJB470002);江苏高校优秀学科建设工程资助项目
2015-03-31修改稿收到日期:2015-05-08
袁建平 男,研究员,研究生导师,1970年12月生
TH311
A

