合力与分力的关系探究
杨伟


1.合力与两个分力的大小关系
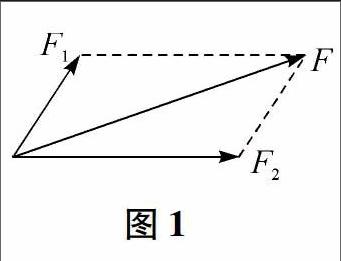
已知两个分力F1和F2,作出平行四边形,两个分力之间的对角线就是两个力的合力,如图1所示.
我们可以用硬纸板手工制作成如图1所示的平行四边形,其中两条边及对角线画上带箭头的线,其余两条边画上虚线,两条边的交接处用小螺丝连起来,可以改变两个分力的角度.明显看出,随着两个分力的角度变大,合力在减小.在变化的过程中,我们可以看到开始合力是大于任何一个分力的,随着两力夹角的增大,某个时候可以等于其中一个分力,夹角再变大可以小于某个分力.所以合力的大小可以比分力大,可以等于分力,可以小于分力.当两个分力夹角为0°时,合力最大,为F1+F2;当两个分力夹角为180°时合力最小,为|F1-F2|,所以合力的范围是|F1-F2|≤F≤F1+F2.
例1 关于合力的下列说法,正确的是()
A.几个力的合力就是这几个力的代数和
B.几个力的合力一定大于这几个力中的任何一个力
C.几个力的合力可能小于这几个力中最小的力
D.几个力的合力可能大于这几个力中最大的力
析假 设两个分力大小为3N和4N,可得它们的合力为1N≤F≤7N,F可以大于4N,可以等于3N、4N,可以小于3N.合力与分力的大小无必然关系,所以本题选择CD.
2.合力与分力等效替代关系
合力与分力从逻辑关系上看,是作用效果的等效替代.分力的共同作用与合力相同,所以合力可以代替几个分力,或者用几个分力共同作用代替合力.
(1)用分力代替合力
例2 如图2所示,α= 30°,装置的重力和摩擦力均不计,若用F=100N的水平推力使滑块B保持静止,则工件上受到的向上的弹力多大?
解析 将F按力的作用效果分解,如图3所示,F1是沿杆方向上的分力,F2是使物体B压紧平面的分力.F1又产生如图4所示的两个作用效果的力,FN是使装置压紧T件的力,FT,是使T件向左的分力,所以T件受到向上的弹力数值上等于
小结 这题也可以采取对B和杆的上端分别进行受力分析,然后根据平衡条件解出.但是学生在实际做题时会出现研究对象搞不清,这时可以将力从作用效果上来分解,还是很容易理解的.
例3 如图5所示,在倾角0=30°的粗糙斜面上放一物体,重力为G,现在用与斜面底边平行的力F=G/2推物体,物体恰能在斜面上斜向下匀速直线运动,则物体与斜面之间的动摩擦因数是多少?
解析 对物体受力分析,发现这些力不在一个面上,要求的滑动摩擦力与F在一个斜面上.我们会在斜面所在平面上依据平衡条件求滑动摩擦力.这时我们可以将物体的重力分解为垂直于斜面向下和沿斜面向下两个方向的分力G1和G2,用G1和G2来代替G.如图6所示,在垂直于斜面的方向上,物体受到的支持力Ⅳ和重力的分力C1平衡,支持力N=Gcosθ.再对物体在斜面上进行受力分析如图7,三力平衡,由勾股定理得
用分力代替合力可以将立体的图转换为两个平面的图,这样解题就简单了.
(2)用合力代替分力
例4 如图8所示,粗糙的斜面体M放在粗糙的水平面上,物块m恰好能在斜面体上沿斜面匀速下滑,斜面体静止不动,斜面体受地面的摩擦力为F1;若用平行于斜面向下的力F推动物块,使物块加速下滑,斜面体仍静止不动,斜面体受地面的摩擦力为F2;若用平行于斜面向上的力F推动物块,使物块减速下滑,斜面体仍静止不动,斜面体受地面的摩擦力为F3.则()
解析 先对滑块受力分析,如图9所示,因为物体匀速下滑是平衡态,所以N和f的合力与重力等值、反向、共线.用F合代替N和f.对斜面受力分析如图10所示,根据牛顿第三定律,N和f的合力竖直,所以F1=0.当然,判断F1可以将m和M看成一个整体进行受力分析,因为两者都处于平衡态,图8中的第2个和第3个图中的推力方向沿着斜面的方向,物体仍然沿斜面下滑,当对物体受力分析时发现,Ⅳ不变,而f是滑动摩擦力,f=μN,N没有变化,所以f也不变.所以,再对M受力分析,N和F的合力跟原来一样,竖直向下,等于物体的重力mg,所以,M相对于地面还没有运动趋势,所以F2和F3都为零.故选D.
小结 本题中,假如对M受力分析,判断N和f的在水平方向的大小关系,要将两个力分解比较,必须将m受到的N和f在水平方向上分解,这样做,也能得到结果,但就繁了.
在碰到合力与分力应用时,要根据实际情况来选择,只要使问题的解决变得简单即可.但是注意,合力与分力不是物体的额外受力,在计算时不能重复计算.

