常见接触面的类型及弹力的分析

张秀亮

摩擦力和弹力是力学中两种基本力，均属于接触力，摩擦力又是比较生涩难懂的力，并且弹力是摩擦力存在的前提，有摩擦力必有弹力.

一、常见接触面的类型

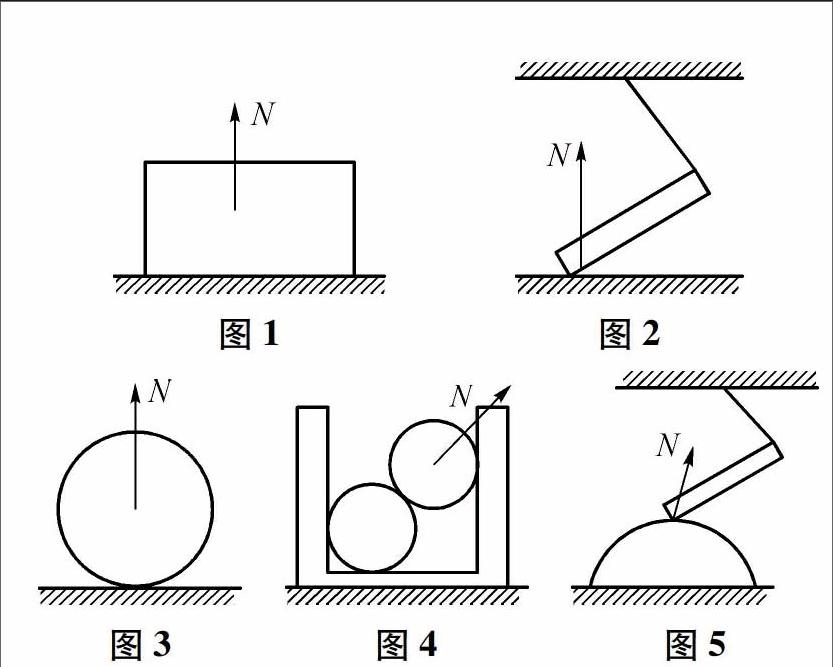
1.平面与平面，如图1所示.

2.点与平面，如图2所示.

3.平面与曲面，如图3所示.

4.曲面与曲面，如图4所示.

5.点与曲面（杆子所受的力），如图5所示.

弹力是力的表现形式之一，是矢量，即有方向，弹力方向的判断是对这个力研究的难点，也是突破口.因弹力是物体在发生弹性形变时为恢复原状而对与之接触的物体的作用，属于接触力且与接触面垂直，则可知弹力的方向与恢复方向一致，与形变方向相反.

二、弹力的分析

1.弹力有无的判断

（1）直接判断法：直接由弹性形变的方向判断弹力的方向.

例1 如图6所示，物块放在水平面上，由于地面受到物块的挤压，发生了向下的形变，由于要恢复成原状，则会对与之接触的物块作用一个竖直向上的弹力.

（2）假设法：因物体所受的力并不是很明显，属于极其微小的形变，且是硬硬接触，则可用假设法来解决此类问题.

例2 如图7所示，试判断小球是否受斜面的弹力？如果有请作出力的图示.

解析 由图中可见绳子垂直于天花板，如果球受斜面的弹力则绳子将会偏移竖直方向，所以球不受斜面的弹力.

（3）计算法：需要进行计算的受力分析问题，往往比较复杂，在于研究对象较多，需借助于数据来判断，如由共点力的平衡条件来决定.

例3 如图8所示，有一质量为M的斜面固定在天花板上，另一质量为m的小物块受到大小为mg的力F作用，处于静止状态，则小物块受几个力？

解析 由物体处于静止状态可知，物体只可能受重力和外力F，因F=mg则物块所受合外力为0，若再受到斜面的弹力，则物块不能处于静止状态.

2.弹力的方向

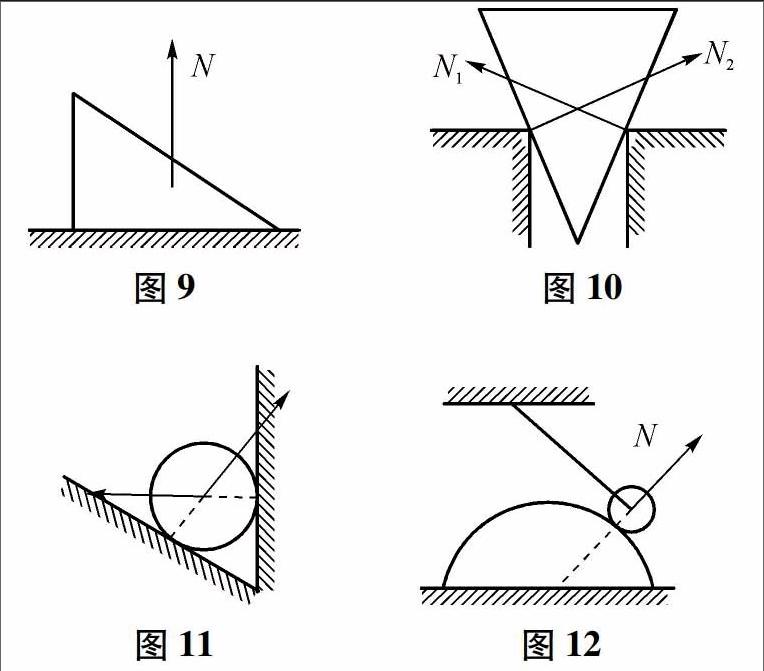
（1）面与面接触弹力的方向：垂直于接触面，指向受力物体，如图9所示.

（2）点与平面接触弹力的方向：过接触点或接触面的切线垂直于接触面指向受力物体，如图10所示.

（3）平面与球面接触弹力的方向：垂直于切面，指向球心，如图11所示.

（4）球面与球面接触力的方向：过接触点且垂直于切面指向球心，如图12所示.

三、弹力的计算

例4如图13所示，一个质量为m的球形物体静止于光滑水平面上，并与竖直光滑墙壁接触，4、B两点是球跟墙和地面的接触点，则下列说法中正确的是（）

A.物体受重力、B点的弹力、A点的弹力作用

B.物体受重力、B点的竖直向上的支持力作用

C.物体受重力、B点的弹力及地面的弹力作用

D.物体受重力、B点大小为mg的弹力、A点的作用力为0

解析 假设将光滑墙壁拆去，小球并不会左右滚动，可见小球并未受到A点的弹力，A错误；B点对小球的竖直向上支持力和地面对物体的弹力实为一个力，只是命名不同，C错误；小球所受的重力和地面对小球的支持力是一对平衡力，所以BD正确.

例5如图14所示，小球4的重力为G=20N，上端被竖直悬线挂于O点，下端与水平桌面相接触，悬线对球A、水平桌面对球A的弹力大小不可能为（）

解析 小球A处于平衡状态，悬线对球A的作用力只能竖直向上，由平衡条件可得：T+N=G，所以D不可能，A、B、C均正确.

例6 如图15所示，质量为m的球置于斜面上，被一个竖直挡板挡住.在水平面上做匀速直线运动，以下说法中正确的是（）

A.因匀速运动，竖直挡板对球的弹力可能为零

B.若加速运动，斜面对球的弹力可能为零

C.斜面和挡板对球的弹力的合力等于mg

D.挡板对球的弹力不仅有，而且是一个定值

解析 小球在重力、斜面的支持力和挡板的弹力作用下做匀速运动，则球受到的合外力为零，斜面和挡板的合力与重力平衡，CD正确，因匀速运动，挡板对小球一定有作用力，A错误，若向右加速，球可能离开挡板，B正确，综上BCD正确.

由于形变很微小，有时根据其形变的情况对弹力有无做出直接判断，此时可采用假设法，复杂情况还可能采用计算法.

弹力大小的基本计算往往利用二力平衡求解.endprint