运用微元法处理“非线性”变化物理问题

刘成华

(前黄高级中学 江苏 常州 213161)

非线性变化的物理问题往往都比较复杂，比如变力做功问题、非匀变速运动位移问题、安培力冲量问题等等.有些非线性变化问题可以用“图像面积”来解决[1]，但还有许多非线性变化的问题用图像解决不了.本文意在阐述运用“微元法”来解决非线性变化的物理问题.

微元法是将连续的研究对象(物体或物理过程)进行无限分割，从其中抽取某一微小单元进行讨论，从而找出被研究对象变化规律的一种思想方法.用微元法解决物理问题是对选取的微元(一个微小部分或微小过程)进行分析研究，确定其受力、运动或状态变化等等.运用微元法的目的，就是为了将不易分析、难以确定的研究对象或物理过程分割到足够小，小到可以近似处理为简单、基本、可研究的问题，最后再积零为整，把所有局部范围内研究的结果累积起来，就可以得到问题的最终解决.

1 运用微元法解决非线性变化外力做功问题

对于恒力做功，可以利用公式W=Fscosα直接求出；但对于变力做功如何求解呢？

【例题1】如图1所示，质量为m的物体以恒定速率v沿半径为R的竖直平面内圆环轨道运动，已知物体与竖直轨道间的动摩擦因数为μ，试求物体从轨道最低点运动到最高点过程中，摩擦力做的功.

图1

解析:物体沿竖直圆轨道从最低点匀速率运动到最高点的过程中，在不同位置与圆环间的压力(图2)，由

得

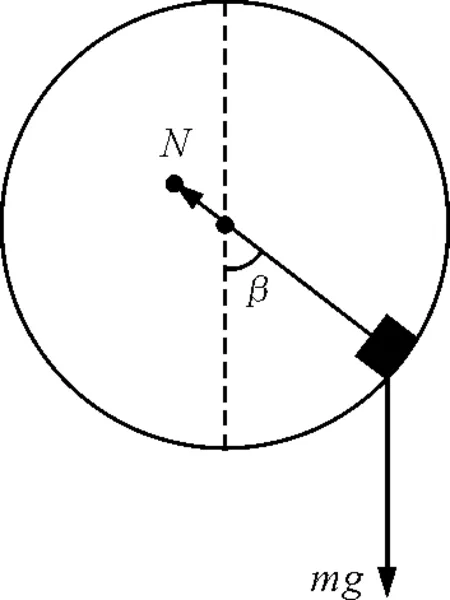
图2

而摩擦力为

f=μN

可见摩擦力f是关于余弦函数变化的，是非线性变化的力，它的功不能简单的用W=Fscosα来求得.可由圆轨道的对称性，在圆轨道水平直径上、下各取两对称位置A和B(图3),设OA、OB与水平直径的夹角为θ，取微元Δθ，则圆弧Δs=RΔθ的足够短可看作直线，且摩擦力可视为恒力，则在A、B两点附近的微元Δs内，摩擦力所做的功之和可表示为

ΔWf=-μNARΔθ+(-μNBRΔθ)

图3

又因为物体在A、B两点以速率v做圆周运动，所以

综合以上各式得

ΔWf=-2μmv2Δθ

故摩擦力对车所做的功

Wf=∑ΔWf=∑-2μmv2Δθ=

-2μmv2∑Δθ=-πμmv2

这题是一个复杂的变力做功问题，利用公式直接求功是难以办到的.利用微元思想，把物体的运动过程无限细分，在每一份位移微元内，力的变化量很小，可以忽略这种微小变化，认为物体在恒力作用下的运动；接下来把所有位移内的功相加，即“无限求和”，则总功就可求得.

2 运用微元法解决速度呈非线性变化的运动物体的位移

【例题2】从地面上以初速度v0竖直向上抛出一质量为m的球，若运动过程中受到的空气阻力与其速率成正比关系，球运动的速率随时间变化规律如图4所示，t1时刻到达最高点，再落回地面，落地时速率为v1，且落地前球已经做匀速运动．求：

(1)球从抛出到落地过程中克服空气阻力所做的功；

(2)球抛出瞬间的加速度大小；

(3)球上升的最大高度H．

解析：从题给v-t图可知，球运动速率变化是非线性变化的，而球在运动过程中受到的空气阻力与速率成正比关系，所以球受到的阻力同样为非线性变化的，运动过程中的加速度也是非线性变化的.

图4

(1)整个过程运用动能定理求得克服空气阻力做功

(2)空气阻力f=kv，落地前匀速运动，则

mg-kv1=0

刚抛出时加速度大小为a0，由牛顿运动定律得

mg+kv0=ma0

解得

(3)设上升时加速度为a，由牛顿第二定律得

-(mg+kv)=ma

取时间微元 Δt内，速度变化 Δv,在极短时间内可认为是匀变速运动，则有

又

vΔt= Δh

上升全程

则

本题第(3)问是一个求非匀变速运动位移问题;上升运动过程加速度呈非线性变化，不能够直接运用运动学公式及牛顿运动解题.运用微元思想，把物体的运动无限细分，在极短时间内加速度变化很小，可认为是匀变速运动，对微元过程运用运动学公式列方程.

3 运用微元法解决加速度呈非线性变化的运动物体的时间

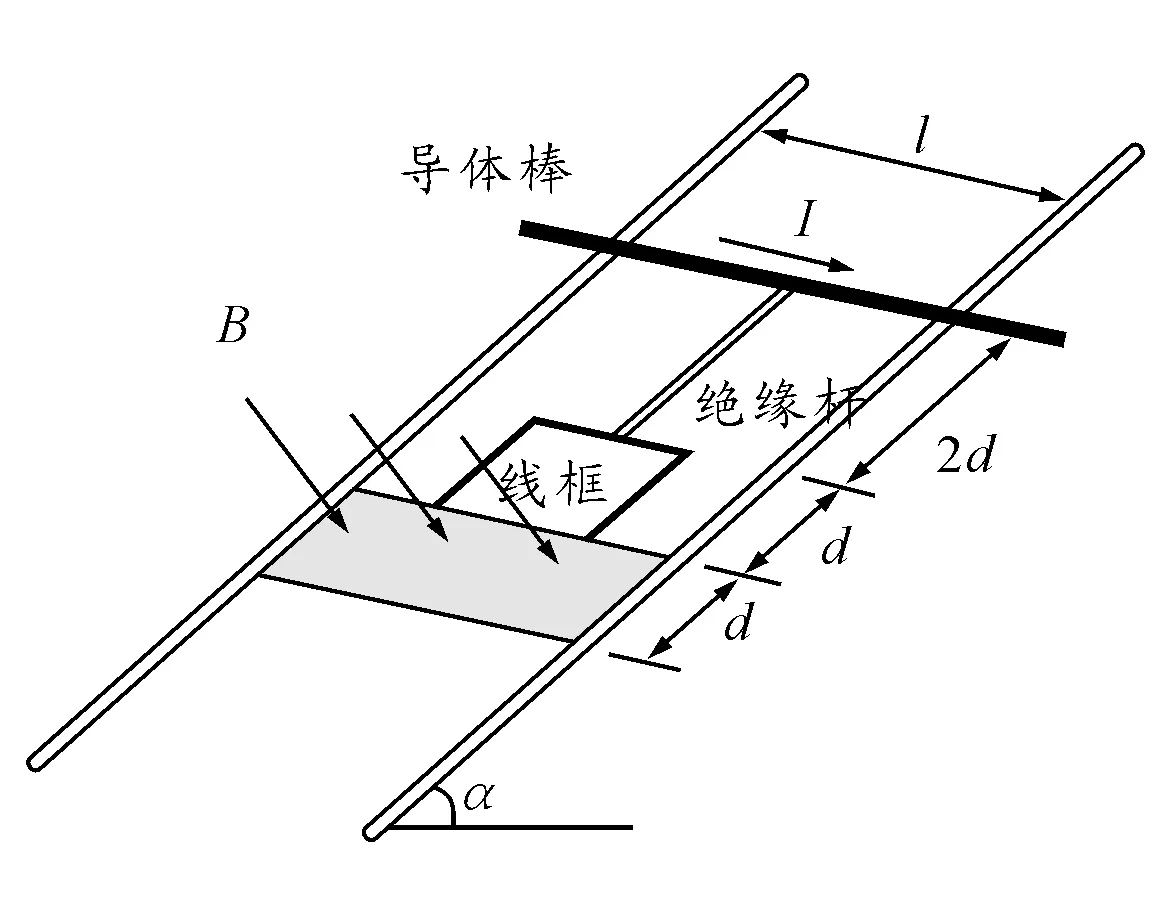
【例题3】如图5所示，两平行的光滑金属导轨安装在一光滑绝缘斜面上，导轨足够长且间距为l,电阻忽略不计，导轨平面的倾角为α.条形匀强磁场的宽度为d，磁感应强度大小为B、方向与导轨平面垂直.长度为2d的绝缘杆将导体棒和正方形的单匝线框连接在一起组成如图所示装置，总质量为m，置于导轨上.导体棒中通以大小恒为I的电流(由外接恒流源产生，图中未图出).线框的边长为d(d

图5

求：(1)装置从释放到开始返回的过程中，线框中产生的焦耳热Q；

(2)经过足够长时间后，线框上边与磁场区域下边界的最大距离xm.

解析:线框下边框进入磁场后产生感应电动势，回路中产生逆时针方向的电流.线框上边框进入磁场后回路中产生顺时针方向的电流.线框总是受到沿斜面向上的安培力而减速，使之进入磁场后的速度随时间的变化呈指数衰减，线框所受安培力也将按指数衰减，则装置的加速度也将按指数衰减，呈非线性变化.这样一个复杂的物理规律，也可用微元法求出其数学表达式.

(1)设装置由静止释放到导体棒运动到磁场下边界的过程中，作用在线框上的安培力做功为W.由动能定理有

mgsinα·4d+W-BIld=0

且

Q=-W

解得

Q=4mgdsinα-BIld

(2)经过足够长时间后，线框在磁场下边界与最大距离xm之间往复运动.由动能定理

mgsinα·xm-BIl(xm-d)=0

解得

本题是2009年高考江苏卷物理学科第25题中两问.

通过以上例题可以看出运用微元法的一般解题思路：

(1)隔离选择恰当微元作为突破整体研究的对象,微元可以是一小段线段、圆弧、一小块面积、一个小体积、小质量、一小段时间……但应具有整体对象的基本特征；

(2)将微元模型化(如视作点电荷、质点、匀速直线运动、匀速转动……)并运用相关物理规律，求解这个微元与所求物体的关联；

(3)将一个微元的求解结果推广到其他微元，并充分利用各微元间的对称关系、矢量方向关系、近似极限关系，对各微元的解出结果进行叠加，以求出整体量的合理解答.

微元的选取应遵循的原则：

(1)所选取的微元必须具有代表性，即微元应具有物体的某些物理特征，如代表物体的受力特征、运动特征、状态变化特征等.

(2)所选取的微元必须与所求物理量相关联，这样才能通过研究微元得到问题的解.

(3)所选取的微元要尽量简单，这样有助于建立简单的物理模型，易于研究分析.

微元法是分析、解决物理问题中的常用方法，也是从部分到整体的思维方法.用该方法可以使一些复杂的物理过程用我们熟悉的物理规律迅速地加以解决，使所求的问题简单化.在使用微元法处理问题时，需将其分解为众多微小的“元过程”，而且每个“元过程”所遵循的规律是相同的，这样，我们只需分析这些“元过程”，然后再将“元过程”进行必要的数学方法或物理思想处理，进而使问题求解.使用此方法会加强我们对已知规律的再思考，从而引起巩固知识、加深认识和提高能力的作用.

参考文献

1 刘成华.用图像面积研究非线性问题.物理教师，2007(11)：47