静电平衡状态下导体球的电荷分布

陈星 朱俏燕

(无锡市第一中学 江苏 无锡 214031)

1 引言

孤立导体的电荷分布已经多有研究[1～2]，但静电平衡状态下导体电荷分布的定量研究稍显少些[3]，尤其是导体接地与否对电荷分布的影响方面的研究.本文就是以导体球为例，通过求解空间电势并利用导体边界条件中电势与电荷面密度的关系探讨导体球在两种典型电场中静电平衡下的电荷分布[4].

2 两种典型电场中导体球的电荷分布

2.1 无穷大匀强电场中不接地导体球的电荷分布

假设不带电的导体球放入如图1所示的匀强电场中，导体外空间无电荷分布.

图1

欲求该导体球的电荷分布，可求解其电势在导体外空间轴对称情形下的拉普拉斯方程

▽2φ=0

(1)

(2)

其中，φ为导体外空间的电势，它是由匀强电场和导体球共同激发的.匀强电场无穷大，所以，可以规定O处的电势为零.而导体是等势体，所以全空间的边界条件为

代入上述通解.

取n=1

由

得

由

有

aRcosθ=-E0Rcosθ

得

可得φ的特解

(3)

根据静电平衡时的导体边界条件，导体球的电荷面密度

3ε0E0cosθ

(4)

取 3ε0E0=1，根据(4)式，可以画出导体球面密度σ随θ的变化关系，如图2(a)所示.由此图还可示意画出导体球表面电荷分布，如图2(b)所示.

由图2可见，在无穷大匀强电场中，不接地导体球达到静电平衡后，在其两端将分别带上异号电荷，并会按照导体球的中轴线按余弦规律对称分布.所以，导体球带的总电荷为零.这也恰好验证了导体静电感应规律，即在靠近正电荷的端感应出负电荷，在靠近负电荷的端感应出正电荷.但感应电荷的总量为零.

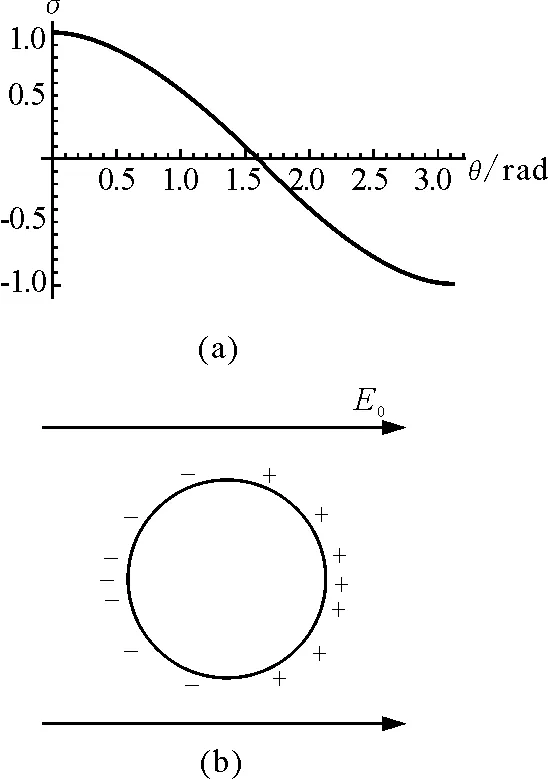
图2

2.2 无穷大匀强电场中接地导体球的电荷分布

现在假设原来不带电的导体球放入匀强电场中，并使其接地，如图3所示.求导体球的电荷分布.

图3

在导体球外空间，仍然可以列出电势的轴对称情形下的拉普拉斯方程，其形式与(1)、(2)式无异.而边界条件也仍然是

可见，接地与不接地的拉普拉斯方程及边界条件是一样的;所以，电势的解也是一样的.因而接地时的导体电荷面密度分布与不接地时相同，如图2(a)和图2(b)所示.这可能与我们的直觉不太一样.从静电平衡的角度看，导体球所处的位置似乎电势应该大于零，导体接地后，电子将由低电势(大地)流向高电势(导体球).但事实上，由于电场无穷大，故在其中任意一点都可以看成是既远离正电荷、又远离负电荷的零电势点，所以，放入其中的导体球接地后，由于是零电势与零电势相连，就不会有电子从大地流向导体球，也不会带多余的电荷.所以，在无穷大匀强电场中，导体球接地与不接地都不会影响其按余弦规律对称分布的电荷.

2.3 点电荷电场中的接地导体球的电荷分布

由于空间有了点电荷分布，所以，不能再通过解拉普拉斯方程来求解空间电势φ.这时，可以采用镜像法.

如图4(a)，假设导体内有一个电荷Q′ ，导体接地时，在Q′和Q的作用下，使导体球成为零等势体，于是可得

△OPQ′∽△OQP

由此，可解出

图4

则在图4(b)中空间任意一点P处的电势就为

(5)

导体球上的电荷面密度

(6)

图5

从两图中可见，在点电荷电场中，导体球接地后，将完全带上与点电荷极性相反的电荷，并将不均匀的分布在导体球表面.其中，靠近点电荷的部分电荷面密度大一些，远离点电荷的部分电荷面密度小一些.从静电平衡的角度讲，在这样一个正的点电荷的电场中，其电势为正.所以，导体球接地后，电子将会由低电势(大地)流向高电势，故导体球会带上负电.

2.4 点电荷电场中不接地导体球的电荷分布

当导体球不接地时，根据导体的静电平衡条件，导体仍然是等势体.与上述接地情形类似，先假定在导体球内有一个假想电荷Q′，在Q′和Q的作用下使导体成为零等势体.则仍然可有

但导体未接地，它当然也不是零等势体.这时，我们可以再在导体球的中心处假想有一个点电荷Q″，在Q″、Q′和Q的共同作用下，使导体球成为满足条件的非零等势体,如图6所示.

图6

对于整个导体球而言，由静电场的高斯定理，它的总电通量应该为零，故有

于是，导体球外空间任意一点P的电势为

(7)

导体球的电荷面密度

(8)

如果把接地与不接地两种情形进行对比，还可发现：从不接地到接地，将有电子从大地流向导体球，流上来的电量要不仅仅中和掉原来左侧的正电荷，还要使其带上与之相反的负电；同时，还要补充右侧负电荷量，使其在σ轴上有一个整体的下移.但观察(6)式和(8)式及图5(a)和图7(a)很容易发现，接地与不接地，σ关于θ的变化函数仅仅差一个常数项；接地时仅仅是不接地时σ的一个上移.所以，不论接地与否，电荷面密度关于角度的变化走向是相同的.如果在导体球的两端分别连接一个验电器，则由以上分析可判断，当导体未接地时，左右两边验电器箔片都会张开；接地后，左边箔片将会先闭合再张开，而右边箔片张角将会在原来的基础上变大.

参考文献

1 吕长荣，刘晓军，高红. 电磁学. 哈尔滨：哈尔滨工业大学出版社，2000. 48

2 韩素红. 关于孤立导体表面电荷分布的讨论. 大同职业技术学院学报，2004(4)：31

3 李敬. 导体表面的电荷分布. 云南大学学报(自然科学版)，1998，20(31)

4 郭硕鸿. 电动力学. 北京：高等教育出版社， 1997. 61