电势与零电势参考处的选择
柳建国, 陈 钺
电势与零电势参考处的选择
柳建国, 陈 钺
(湖南理工学院 物理与电子学院, 湖南 岳阳 414006)
探讨了零电势参考处的两种常用选择方法, 及其两种不同电势零点参考处选定后, 不同电势函数之间的相互转换关系, 重点分析该变换关系的应用, 可方便、简单地求解很难的实际物理问题.
电势; 零电势; 无穷远; 变换关系
静电场中的电势能, 电势与重力场中的势能一样: 仅具有相对意义, 只有选定了零电势参考处后, 电势分布才唯一确定. 选取不同零电势参考处时, 其电势分布函数仅相差一常量项. 虽然零电势参考处可以任意选取, 但适当的选择, 往往可使问题简化, 且电势分布的物理内涵更明确.
教材中基本选取无穷远处为零电势参考处, 但工程中、日常生活中、生产中却常常要取指定点为零电势参考处. 怎么结合处理, 怎么处理才更方便?
1. 首先分析、探讨分别选取两不同零电势参考处时, 电势分布函数的两种表达函数之间的相互关系:
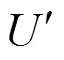



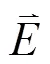
例1 长度为的线段均匀带电荷, 试求其所激发的静电场电势分布.
解 (1)如图1所示, 建立柱坐标系, 取轴沿线段,中点为坐标原点.
(2) 取无穷远处为零电势参考处, 将带电体分成无穷多电荷元:
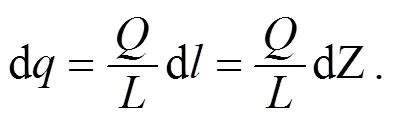
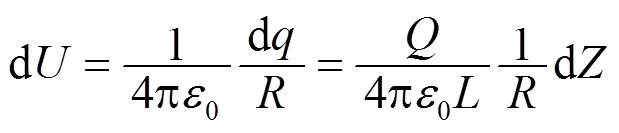
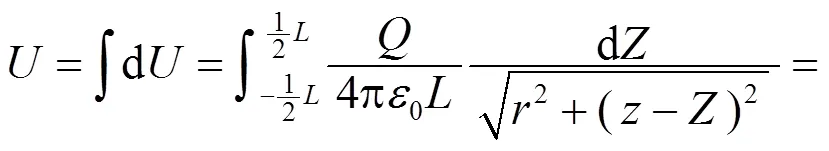
图1

例2 试求无限长带电直线(电荷线密度为) 所激发的电场在空间的电势分布.
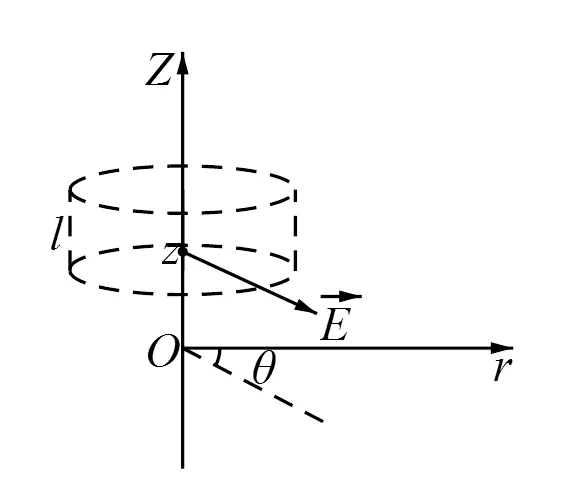
图2
解如图2所示, 建柱坐标系, 取该带电直线为轴.
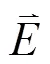
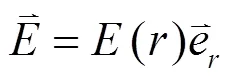
(3) 用电势定义式求电势分布.

取= 1m(即取以轴为轴半径为1 m的等势圆柱面为零电势参考处), 则
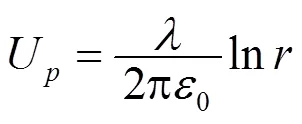
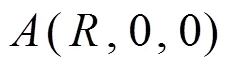
解 (1) 该电荷系统激发的电场, 采用例1的以无穷远处为零点电势参考处的电势分布函数可以求得
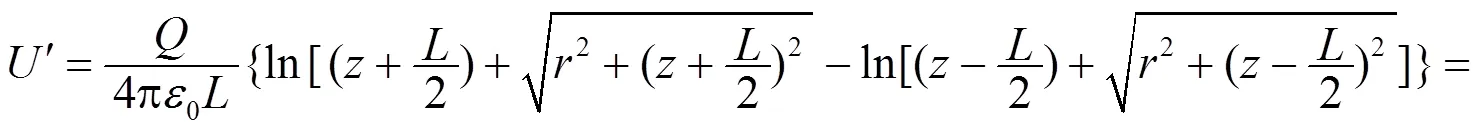
(2) 根据两不同零电势参考处电势函数的变换关系式(1), 可求得




有了取不同零点势参考处时, 电势函数的相互变换关系式(1)、(2), 不但可以加深对电势概念的理解, 也为我们求电势分布提供了方便省时的方法.
[1] 梁绍荣. 普通物理学第三分册电磁学[M] . 第3版. 北京: 高等教育出版社, 2005
[2] 程守诛, 江之永. 普通物理学[M]. 第6版. 北京: 高等教育出版社, 2006
Option of Electric Potential and Zero Potential Reference
LIU Jianguo, CHEN Yue
(College of Physics and Electronics, Hunan Institute of Science and Technology, Yueyang 414006, China)
In this paper, we discuss two kinds of commonly used selection method of zero potential reference and the different transformation relationship between electric potential function after two different potential zero references are selected, mainly analyze the application of the transform relationship, it can be convenient and simple to solve difficult practical physical problems.
electric potential, zero potential, infinity, transformation relation
2017-07-22
柳建国(1957− ), 男, 湖南长沙人, 湖南理工学院物理与电子学院副教授. 主要研究方向: 无线电电子学、物理教学与研究
O441
A
1672-5298(2017)04-0017-03

