纤维层面密度的光学新算法

吴美琴,王府梅,b

(东华大学 a. 纺织学院； b. 纺织面料技术教育部重点实验室，上海 201620)

纤维层面密度的光学新算法

吴美琴a,王府梅a,b

(东华大学 a. 纺织学院； b. 纺织面料技术教育部重点实验室，上海 201620)

为了寻求通过测量光学信号计算各种纺织纤维集合体的面密度分布的准确方法，针对纺织纤维对光具有吸收、反射和散射的特性，基于Kubelka-Munk双通道模型透射公式，推导出通过光学信号计算层状纤维集合体任意一点处的相对面密度的算法，称为Wu-Wang(W-W)透射算法.采用已知面密度的棉纤维和羊毛纤维试样各一组，借助数码光学元件搭建的装置测得纤维层的透射光图像，以W-W算法计算出各试样的相对面密度，发现与其他方法测试的基准面密度高度吻合.并与Lambert-Beer模型的计算结果作比较，证明W-W算法获得的光学相对面密度与真实面密度非常吻合，验证了此面密度算法表征的相对光学面密度的准确性. W-W新算法可以广泛应用于纤维长度分布和多种结构的纤维集合体面密度的测量.

纤维集合体； 面密度； Kubelka-Munk； 光透射； Wu-Wang算法

层状纺织纤维集合体的面密度分布是表征纤维层结构和质量分布等特性的中间变量，是研究纤维、纱线、织物等纤维集合体结构和性能的重要依据.纤维集合体的面密度分布被广泛应用于纺织材料的光电法检测等领域，如照影仪测量纤维长度法[1-2].

早期光电法测量纤维层厚度时，将透光量作为纤维层的厚度，但存在较大的偏差[1]，因为透光量与纤维层厚度不是线性关系.后来，基于单向吸收作用的Lambert-Beer定律[3]被广泛用于材料厚度的测量和计算，包括纤维层的厚度计算[4-7]，这在一定程度上改善了纤维层光学厚度的测量计算精度[7].但是，由于纤维层是半透明的线形材料集合体，当光照射透过纤维集合体时，除被吸收、透射外，纤维层内部还存在各个方向的散射光、各根纤维表面产生的反射光和纤维内部消光剂等嵌入物或结构不均匀产生的散射光，这些不可忽略的纤维集合光学信号使基于仅考虑吸收的Lambert-Beer定律计算的纤维层面密度仍然存在明显偏差.文献[7]利用数个品种的细绒棉试验总结出棉纤维须丛光学面密度修正的经验公式，但此公式只适用于棉纤维长度的测量计算.

许多研究者对纺织纤维的光学性质进行了详细的试验研究与理论分析[8-9]，但是综合考虑吸收、散射和反射的光学面密度研究尚未见报道.

Kubelka-Munk双通道模型[10]将入射光、反射光和散射光在各个方向上的衰减化简为向上和向下两个通道方向上的衰减，同时考虑光入射方向和反方向两个通道的光吸收和光散射，常被应用于油墨纸张[11-13]、颜色混色[14-16]、医药学[17-18]以及膜层原位定量光密度分析[19]等领域，而在纤维集合体面密度测量方面未见应用或研究报道.

为了寻求可以广泛适用于各种纺织纤维集合体的由光学信号计算其面密度分布的准确方法，本文考虑纺织纤维对光线具有吸收、散射和反射的特性，在Kubelka-Munk双通道模型透射公式的基础上，进一步推导出由纤维和空气混合构成的层状纤维集合体相对面密度的光学新算法——Wu-Wang(W-W)算法，用试验验证了W-W算法的可行性，并与常用的Lambert-Beer模型的准确度作了对比.

1 与材料厚度相关的现有理论

目前，材料光学厚度的测量计算多采用Lambert-Beer吸收模型[5]，只考虑光线前进方向材料的吸收和散射.

实际上，光照射纤维层时，除了存在光前进方向纤维对光线的吸收和散射作用外，还存在各根纤维表面的反射以及所有反射光方向纤维对光线的再次吸收和散射作用.现有的Kubelka-Munk双通道模型[10]是基于向下(光前进方向)和向上两个通道中光的吸收和散射作用引起的光衰减所建立的膜层厚度计算模型，比Lambert-Beer理论更加贴近真实情况.

1.1 单向吸收和散射的材料厚度理论

根据Lambert-Beer定律，当一束入射光强为I0的平行单色光垂直通过某一均匀非散射的吸光物质时，存在以下理论关系式[5]：

I=I0e-(K+S)X

(1)

(2)

其中：I为透过材料的光强，cd；K为材料吸收系数，指单位厚度材料吸收光能的百分数， cm-1；S为材料散射系数，指单位厚度的材料散射光能的百分数，cm-1；X为材料厚度， cm；T为材料的透射率，指透过材料的光通量与入射光通量之比.

在纤维材料领域，至今仍然忽略材料散射系数S，即运用式(3)计算纤维材料厚度X.

I=I0e-KX

(3)

1.2 双向吸收和散射与材料厚度的关系

1931年，Kubelka和Munk建立了可以同时进行光吸收和光散射的材料厚度相关的材料光学方程，也被称作Kubelka-Munk(K-M)模型，此模型被快速应用于颜色、医药、大气等领域的研究，主要适用于透明和半透明的光介质材料(纸张、涂料等). K-M模型的建立基于如下假设：

(1) 光介质形成一个有限厚度的片层结构，光学作用不受边缘的影响；

(2) 假设该介质在光学角度上为均匀介质，光被散射时存在的光学不匀尺寸远小于试样的厚度和材料中颗粒的尺寸；

(3) 在光线进出介质时，原则上假设介质的媒介是相同的，通常是空气；

(4) 光在介质的一侧照明，除了在有基底背衬的情况下，假设被反射和散射的光不再被反射或散射回试样；

(5) 假设不考虑选择性吸收和散射引起的波长分布的变化；

(6) 理论上，假设在入射光的光谱范围内，光是均匀入射介质的，即使光是非均匀入射介质，通常也可以证明介质对不同波长的光是非选择性的.

在以上假设条件下，利用积分法分析光前进方向及其反方向上漫射光的光强由于散射和吸收作用发生的衰减情况，推导出光线穿透均质片状材料时材料的K、S、X与T、反射率R之间的定量关系，即为K-M模型. 式(4)为K-M模型的变形形式[10].

(4)

当材料厚度增加到足够厚时，即X→∞时，coth(b SX)→∞背衬层的背景效应消失，其中，coth(x)为双曲余切函数，coth(x)=(ex+e-x)/(ex-e-x)，此时，

(5)

(6)

(7)

2 建立纤维集合体面密度计算模型

2.1 纤维层面密度函数的光学方程

纤维集合体不同于Lambert-Beer模型和K-M模型考虑的均匀光学介质(液相或固相的单相材料)，其是空气和半透明纤维固体材料的混合材料.

为了建立固相和气相材料混合的纤维集合体面密度的光学方程，首先建立纤维集合体的结构示意图和坐标系，如图1所示.为作图方便，图1(a)采用了纤维平行排列的须丛来示意纤维集合体中纤维与空气的混合情况，实际下面理论推导适合于纤维在三维空间随机分布等任意纤维集合体.

(a) 纤维集合体

(b) 纤维集合体横截面几何结构

Fig.1 Schematic diagram and coordinate of the fibers and air mixture material

这里只考虑纤维间空气不含尘埃等杂质的理想情况，所以假设：(1)纤维对光线的吸收和散射作用只发生在各根纤维内部，忽略空气中的悬浮微粒等因素对光线的影响，即光线穿越纤维之间的空气时不发生任何吸收、反射和散射；(2)须丛对光线的反射只发生在各根纤维表面，且将纤维层内部纤维(表层纤维以外)表面反射作用可视为纤维集合体散射的一部分，并沿用K-M模型的全部假设，即光线由x轴方向(向下)垂直入射时，经纤维集合体的光线只存在向上和向下两个方向的光能量的散射和吸收.

对于某一种纤维材料，纤维层吸收系数K、散射系数S、无穷厚时的反射率R∞均为常数. 纤维以任意形态平行排列在y-z平面，如图1(a)所示，其任意纤维层的横截面示意图如图1(b)所示，纤维横截面上任一点在x轴方向的所有纤维厚度的累积值X(即图1(b)中纤维内线段的累计长度)也满足式(4)，纤维层厚度X是y-z平面上的一个函数或变量.

用W或W(y,z)表示纤维层的面密度函数(单位为mg/mm2).对于某一种特定的纤维，其体积密度fw是一个常量，则有

W=fwX

(8)

将式(6)和(7)代入式(4)，解方程得：

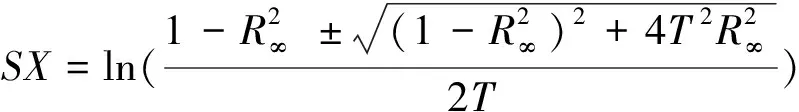
(9)

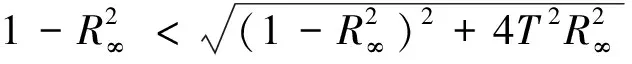
(10)

将式(10)代入式(8)得，纤维层面密度W为

W= fwX=

(11)

式中：fw/bS的值由纤维特性确定.若已知无穷厚度纤维层的反射率R∞、测量获得纤维层在y-z平面上任一点的透射率T(y,z)、该纤维的吸收系数K和散射系数S，就可以计算纤维层的面密度W(y,z).

同理，Lambert-Beer模型式(4)两边分别乘以纤维的体积密度fw，可得

(12)

若已知纤维层在y-z平面上任一点的透射率T(y,z)和光学参数K及S，可以计算Lambert-Beer模型下纤维层的面密度WL(y,z) .

实际上，由式(11)和(12)计算纤维层的面密度很难实施，原因在于各种纤维的光学参数K及S通常是未知量，K和S不但与组成纤维的物质有关，还与纤维粗细、天然纤维品种、化纤纺丝时添加的消光剂、表面油剂和后整理助剂含量等因素有关，表面油剂增加了纤维表面反射，消光剂等相关助剂产生光扩散的同时增加了光的衰减，吸收系数和散射系数也同时增加.

2.2 纤维层相对面密度的计算模型

纤维层质量分布的均匀度测量、长度测量等很多情况下，只需要弄清纤维层的相对面密度，即某一点的面密度与最厚处面密度或平均面密度的相对大小. 因此，本文定义纤维层任一点的相对面密度函数Wr为该点的纤维层面密度W与所测量的纤维层最厚处的面密度Wmax的比值，则由式(11)可得

(13)

同理，Lambert-Beer模型下的相对面密度WrL公式为

(14)

式(13)和(14)的应用价值在于不包含未知参数fw/(K+S).只要测得纤维层各点的透射率T、该纤维层无穷厚时的反射率R∞、试样最厚处的透射率Tmax，就可以计算纤维层上任一点的相对面密度Wr(y,z)或WrL(y,z)，可用于纤维集合体材料的很多结构特性的测量分析.式(13)是本文首次推导出的纤维层相对面密度算法，式(14)已经被用于纤维层相对面密度计算[6]. 本文将计算纤维堆砌材料光学相对面密度的算法式(13)称为Wu-Wang算法或W-W算法.

3 W-W算法的试验验证

3.1 试样

为了利用常规纺织仪器、数码成像技术测量层状纤维集合体的面密度，制作了两系列面密度不同的棉纤维和羊毛纤维层试样.每一试样中的纤维呈均匀分布，纤维层排列及测试区域，如图2所示.试样制作方法：(1)利用Y111型罗拉引伸器将棉纤维制成棉条，毛纤维直接采集直径为19.7m的澳洲细毛商品毛条；(2)将棉条和毛条中部扯断，在断面处用夹子夹取梢部的纤维，梳去未被夹子夹住的浮游纤维，然后将夹子上平行排列的纤维平铺在具有正方形测试孔的纸板上，让纤维排列方向与正方形孔的一边平行(参见图2),再夹取第二次、第三次、……、若干次，平铺在正方形测试孔的空隙或纤维比较稀薄的位置，直到形成均匀的一层为止，最后用胶将纤维首尾端固定在支撑的纸板上.棉和毛纤维各制作纤维层厚度依次增加的10个样品，分别编号为1～10，如表1所示.

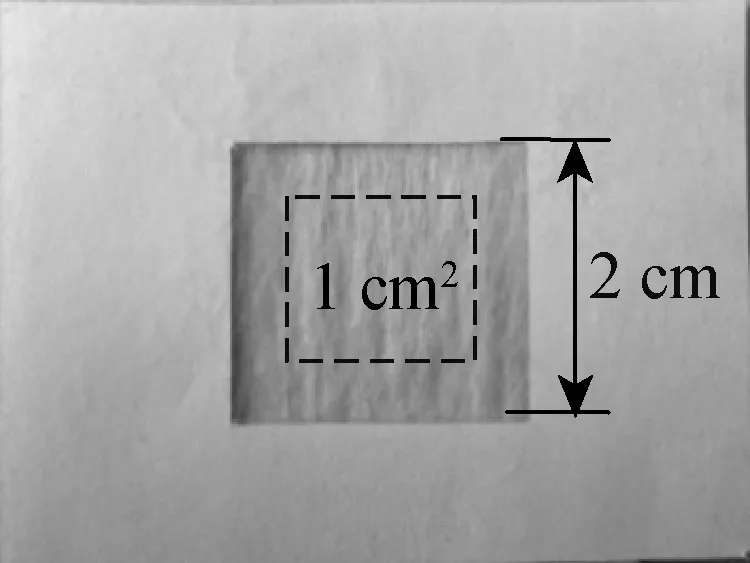
图2 纤维层排列及测试区域Fig.2 Fiber layer orientation and test area

3.2 试样的基准面密度

20个试样首先进行光学测试，光学测试区域为图2中虚线框的(1×1) cm2. 用手术剪将每个试样

表1 纤维层基准面密度

中(2×2) cm2的测试孔内纤维剪下，然后用测量精度为0.01 mg的电子天平称重，计算各试样单位面积的纤维质量W0， 如表1所示，并将其看作纤维层的基准面密度，用于考核光学面密度的计算精确度.

3.3 纤维的光学参数测量

利用UV-3600型紫外可见分光光度仪的黑板衬垫测量“无穷厚”的棉纤维层的反射率R∞，如图3所示，实际纤维层厚度为该仪器能够允许的厚度2 cm.

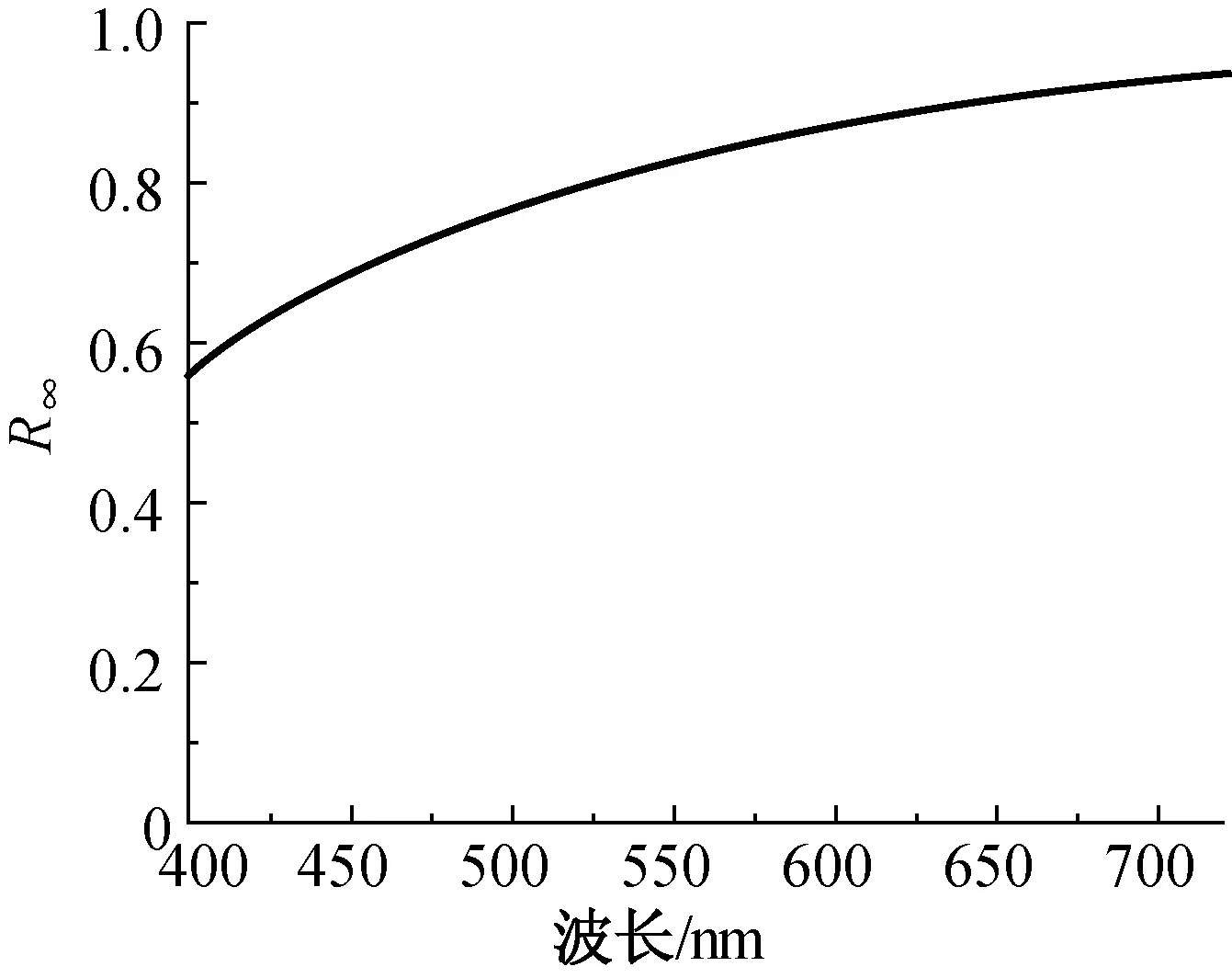
图3 2 cm厚的纤维层反射率R∞随波长的变化情况 Fig.3 The R∞ of the fiber layer with the thickness of 2 cm at different wavelength

由图3可知，在波长380 ～720 nm范围内反射率R∞的取值范围为0.55～0.95.由于仪器只能容纳不超过2 cm厚度的纤维层，实测反射率略小于无穷厚度纤维层的R∞，所以实际的取值范围的上限应略大于本试验的最大值0.95.

3.4 纤维层光学相对面密度的测量

3.4.1 纤维层的透射率

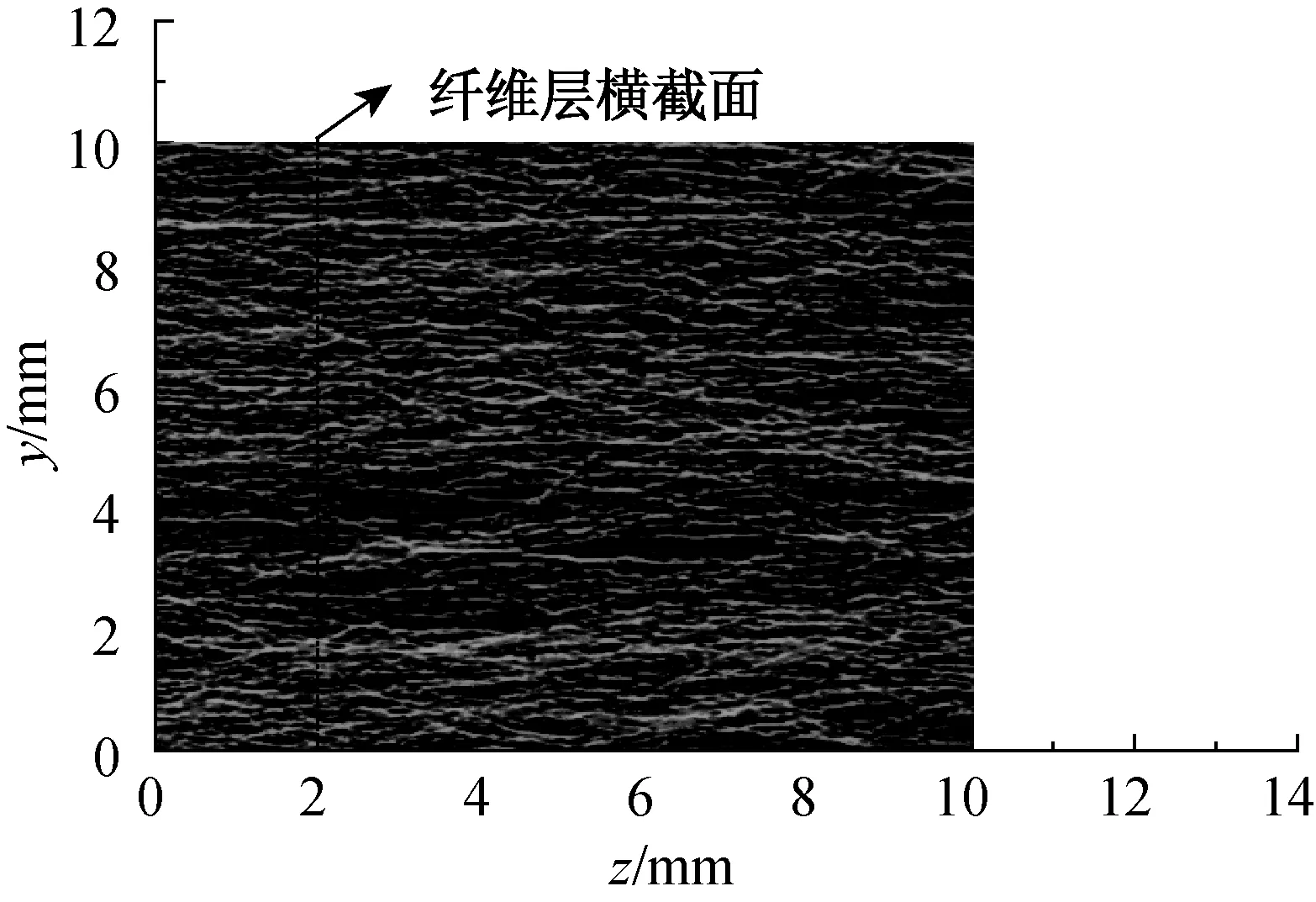
利用高精度数码成像技术，通过软件设定图像分辨率为1 000像素，即每一像素点的边长为25.4m，采用CCD(charge-coupled device)摄像头提取表1所示的棉纤维和羊毛纤维各试样中部(1×1) cm2区域的透射灰度图，如图4所示. 则纤维层图像中任一个像素点的透射率T或T(y,z) 是 (y,z) 平面上的一个变量[4]，如式(15)所示，其中n为该像素点的灰度值，其范围为0～255.

(15)

(a) 棉纤维

(b) 羊毛纤维

Fig.4 The transmission intensity images of the cotton and wool fiber layers

3.4.2 以W-W透射算法计算的光学面密度

由于数码成像技术的光源为复合光，所以需要考查在UV-3600型紫外可见分光光度仪获取的R∞的取值范围内，由式(13)计算得到纤维层的光学平均相对面密度与基准相对面密度的关系.将纤维层透射率T(y,z) 代入式(11)，计算得到表1所示各试样中部(1×1)cm2范围内每个点的光学相对面密度Wr(y,z)，而后对该范围内所有点的相对面密度求平均值，得到该试样的光学平均相对面密度War，War简称为光学相对面密度.

棉纤维和羊毛纤维两组试样的光学平均相对面密度War与其对应的基准相对面密度W0之间的关系如图5所示.

(a) 棉纤维

(b) 羊毛纤维(d =19.73 m)

Fig.5 The relationship between theWarandW0at differentR∞value

由图5可知，由数码成像技术和W-W算法计算得到的光学相对面密度与基准相对面密度有很高的一致性. 并且，对于不同R∞取值，光学相对面密度变化非常小.

R∞取不同值时，计算棉纤维和羊毛纤维两组纤维层试样的光学相对面密度War与其基准面密度W0之间的平均偏倚率δ，如式(16)所示，计算结果见表2所示.

(16)

由表2可知，在R∞=0.98时，棉纤维和羊毛纤维的相对光学面密度的平均偏倚率最小，因此，纤维层光学面密度测量计算采用R∞=0.98. 另外发现，羊毛纤维的偏倚率略大于棉纤维，需要今后进一步测量不同纤维的集合体反射特性.

3.4.3 Lambert-Beer模型和W-W透射算法的差异比较

利用数码成像技术获得灰度值透射图像，分别利用W-W算法和Lambert-Beer模型，取R∞=0.98，计算得到各纤维层试样的平均光学相对面密度，并与基准相对面密度进行比较，如图6所示.

(a) 棉纤维

(b) 羊毛纤维(d =19.73 m)

图6 W-W算法和Lambert-Beer模型的光学相对面密度与基准相对面密度比较

Fig.6 The optical and base relative area density with the W-W algorithm and the Lambert-Beer algorithm

由图6可知，W-W算法得到的光学相对面密度均比Lambert-Beer模型得到的光学相对面密度更加接近试样的基准相对面密度，即W-W算法获得的光学相对面密度较基准面密度有更高的吻合性，说明考虑众多纤维表面反射和纤维内部散射作用汇聚成纤维集合体散射作用的W-W算法，其可以更精确地测量纤维层相对面密度.

由图6还可知，光学相对面密度与基准相对面密度不能完全重合，部分误差来源于两种测试的试样面积大小不同、剪切纤维和称重时的试验误差，这类随机误差引起图6的试验点在45°斜线上下波动.图6(b)中羊毛纤维的试验点几乎全部分布在45°斜线上方，说明可能还存在纤维光学性能自身的原因.首先，羊毛鳞片对光线的反射作用很强，基于K-M模型的W-W算法只考虑第一次反射以及纤维对第一次反射光的吸收和散射，对于羊毛纤维而言，纤维对入射光的第二、第三次反射以及对这些反射光的吸收和散射作用不可忽略不计.其次，毛纤维层的面密度明显大于棉纤维层的面密度，所以也可能造成毛纤维的测量偏差略大于棉纤维.再者，本文采用的R∞=0.98仅仅是一个试验优选值，实际采用数码成像设备为光谱分布未知的复合光源，如果用单色光测量和对应的羊毛R∞计算得到的光学相对面密度无疑会更加准确.今后需要进一步探索考虑纤维对入射光的第二、第三次反射以及对这些反射光的吸收和散射作用的纤维层面密度计算理论或者试验修正方法.

4 结 论

(1) 基于K-M模型推导出适用于计算纤维层中任意一点的相对面密度的W-W透射算法.

(2) 利用紫外可见分光光度仪测量了“无穷厚”棉纤维层的反射率R∞与入射光波长的关系，0.55

(3) 在R∞=0.98条件下，比较 W-W透射算法和Lambert-Beer算法计算得到的纤维层的光学相对面密度与基准相对面密度的吻合程度，发现W-W透射算法得到的光学相对面密度更接近基准相对面密度，由基准相对面密度的平均偏倚率说明W-W透射算法比至今采用的Lambert-Beer理论更适用于纤维层光学相对面密度的计算，可广泛应用于纤维长度分布的测量和各种纤维集合体的结构性能评价.

[1] HERTEL K L, ZERVIGON M G. An optical method for the length analysis of cotton fibres[J]. Textile Research Journal, 1936, 6(7): 331-339.

[2] NAYLOR G R S, DELHOM C D, CUI X, et al. Understanding the influence of fiber length on the high volume instrumentTMmeasurement of cotton fiber strength[J]. Textile Research Journal, 2014, 84(9): 979-988.

[3] STRONG F C. Theoretical basis of Bouguer-Beer law of radiation absorption[J]. Analytical Chemistry, 1952, 24(2): 338-342.

[4] 王建鸣.朗伯-比耳定律的物理意义及计算方法的探讨[J]. 高等函授学报(自然科学版), 2000, 13(3): 32-33.

[5] FISCHER H, RETTIG D, HARIG H. Image processing for measuring the length distribution of reclaimed fibres[J]. Melli and Textile Berichte International Textile Reports, 1999, 80(5): 94-96.

[6] 刘若华, 李汝勤. 照影机曲线的修正研究[J]. 纺织学报, 2002, 23(1): 27-28.

[7] WU H, WANG F. Image measuring method for fiber length measurements[J]. Industria Textila, 2013, 64(6): 321-325.

[8] 赵林, 姚穆. 纤维反光和透光性质的研究[J]. 西北纺织工学院学报, 2001, 15(2): 207-212.

[9] 彭波, 丁天怀, 王鹏. 纺织纤维光散射特性的模拟与实验[J]. 光学学报, 2012, 32(8): 278-283.

[10] KUBELKA P. New contributions to the optics of intensely light-scattering materials: Part I [J]. Josa, 1948, 38(5): 448-457.

[11] DZIMBEG-MALCIC V, BARBARIC-MIKOCEVIC Z, ITRIC K. Kubelka-Munk theory in describing optical properties of paper (I)[J]. Tehnicki Vjesnik, 2011, 18(1): 117-124.

[12] DZIMBEG-MALCIC V, BARBARIC-MIKOCEVIC Z, ITRIC K. Kubelka-Munk theory in describing optical properties of paper (II)[J]. Tehnicki Vjesnik, 2012, 19(1): 191-196.

[13] VAHEY D, ZHU J, HOUTMAN C. On measurements of effective residual ink concentration (ERIC) of deinked papers using Kubelka-Munk theory[J]. Progress in Paper Recycling, 2006, 16(1): 3-12.

[14] YANG L, KRUSE B. Revised Kubelka-Munk theory: I. Theory and application[J]. Josa A, 2004, 21(10): 1933-1941.

[15] YANG H, ZHU S, PAN N. On the Kubelka-Munk single-constant/two-constant theory[J]. Textile Research Journal, 2009, 80(3): 263-270.

[16] BASAK S, GUPTA D. Advanced processing of woollen textile pretreated with UV excimer radiation[J]. Man-Made Textiles in India, 2013, 41(6): 204-209.

[17] MOLENAAR R, TEN BOSCH J J, ZIJP J R. Determination of Kubelka-Munk scattering and absorption coefficients by diffuse illumination[J]. Applied Optics, 1999, 38(10): 2068-2077.

[18] PECHO O E, GHINEA R, IONESCU A M, et al. Optical behavior of dental zirconia and dentin analyzed by Kubelka-Munk theory[J]. Dental Materials, 2015, 31(1): 60-67.

[19] SPANGENBERG B, KLEIN K-F. New evaluation algorithm in diode-array thin-layer chromatography[J]. JPC-Journal of Planar Chromatography-Modern TLC, 2001, 14(4): 260-265.

A New Optical Algorithm for Calculating the Area Density of the Fiber Layer

WUMei-qina，WANGFu-meia,b

(a. College of Textiles; b. Key Laboratory of Textile Science & Technology, Ministry of Education, Donghua University, Shanghai 201620, China)

To search for an accurate method to calculate the area density distribution of all kinds of fiber assemblies by the measured optical signal, and considering textile fibers’ properties of absorption, reflection and scattering, a new optical transmission algorithm that called Wu-Wang(W-W) algorithm was derived. This new algorithm was based on the transmission formula of Kubelka-Munk model and the relative area density at any point of layered fiber assemblies can be calculated. A group of wool and cotton fiber samples were used as test samples, whose base area densities are already known. The transmission information of the fiber layers were measured by a laboratory devices which were set up by digital optical elements. The relative optical area density of the test samples that calculated by W-W algorithm from the transmission information is nearly equal to the results of other methods. This relative optical area density was also compared with the result of Lambert-Beer model. The results show that the optical relative area densities by the new built transmission algorithm are closer to the real ones, which proves the accuracy of the optical relative area densities calculated by the W-W algorithm. The new built W-W algorithm can be used in the measurement of fiber length distribution and area density of different constructions of fiber assemblies.

fiber assemblies; area density; Kubelka-Munk; optical transmittances; Wu-Wang algorithm

1671-0444 (2016)06

2015-10-10

中央高校基本科研业务费专项资金资助项目(CUSF-DH-D-2016014)

吴美琴(1989—)，女，山东淄博人，博士研究生，研究方向为纺织材料检测技术. E-mail: feiying082@126.com 王府梅(联系人)，女，教授，E-mail: wfumei@dhu.edu.cn

TS 101.3

A