棉纤维蠕变与应力松弛行为分析

李 勇 李 健 雷福祥 张洪洲 陈晓川

（1.塔里木大学，新疆阿拉尔，843300；2.东华大学，上海，201620）

原棉是重要的纺织原材料，其结构蓬松、纤维间组织松散，给其初加工、储运环节带来不便。在生产加工过程中，原棉需要不断进行机械压缩、开松。棉纤维集合体材料具有典型的黏弹性力学性能，受载荷作用易蠕变、松弛。

国内外诸多研究者用经典理论、模型研究纤维材料的蠕变与应力松弛行为。DUNLOP J I［1］构建了纤维集合体体积变化模型（库仑模型），其可解释压缩过程中纤维滑移、变形滞后和不可回复等现象。YAMAGUCHIY［2］测试了棉、毛、丝、麻等纤维的拉伸蠕变性能，指出纤维拉伸蠕变与应力和时间相关。王旭等［3］测试了麻赛尔纤维的蠕变和应力松弛性能，表明麻赛尔纤维松弛现象不明显，蠕变现象更为明显。陈康等［4］利用万能试验机测试了聚酯工业丝的蠕变性能，并提出了蠕变载荷与蠕变断裂的预测方法。GAO Xiaoping等［5］研究了地毯纱线在动态加载后的蠕变行为，利用标准线性模型、四单元模型和黏弹性模型等力学模型获得蠕变公式，进行非线性拟合获得蠕变试验数据，预测纱线蠕变伸长率。ASAYESH A等［6］用黏弹性模型分析了平纹织物蠕变力学性能，发现纱线密度增加，织物蠕变量减小。DANIL CHUK E L［7］研究了机织物蠕变性，非线性黏弹模型可表达聚合物织物的蠕变性。NAKAJIMA Chie和YONEDA Morihiro等［8-9］研究了高湿度条件下涤纶、铜氨纤维和莱赛尔纤维填料的压缩蠕变和应力松弛行为，用经验公式模拟各类填料的蠕变和应力松弛行为。

作为典型的黏弹性材料，棉纤维的蠕变与松弛力学行为与其加工应用息息相关，但仍未深入分析。本研究以棉纤维为研究对象，依据棉纤维的压缩蠕变与应力松弛特性建立黏弹塑性本构模型。不同载荷下测试棉纤维的蠕变与应力松弛曲线，分析压缩载荷与其力学指标之间关系，为原棉的生产加工环节提供一定理论指导。

1 试验部分

1.1 材料与仪器

原料为新疆阿拉尔市新陆中37手摘原棉，原棉提取于新疆新越丝路有限公司。FA 1104型电子天平（上海安亭科学仪器厂），FSR400型薄膜压力传感器（Interlink Electronics），有线薄膜压力传感软件（安徽威科电子有线公司），DSCa-01型数字式小样梳棉机（天津嘉诚机电设备有限公司），圆盘取样器（温州大荣纺织仪器有限公司）。

1.2 制样

为使棉纤维取向一致，原棉经小样梳棉机梳理成原棉层，再利用圆盘取样器切出直径90 mm的原棉圆片，逐层叠加，制得棉样（高度30 cm，重量160 g）。

1.3 蠕变回复试验

棉样放置于载样台上（为了防止棉样受压滑移，载样台固装直径为8 mm的定杆，棉样套在定杆上），不锈钢重块加压棉片进行蠕变试验（室内温度19℃～25℃，相对湿度45%～57%），如图1（a）所示。每隔一定时间，薄膜压力传感器采集棉纤维内部压力值，记录棉纤维高度值。蠕变试验结束，即卸除棉纤维压力。每隔一定时间记录棉纤维回复量。蠕变时间600 h，回复时间400 h。对棉纤维依次施加20 N、40 N、60 N、100 N、200 N、400 N、600 N的重块进行蠕变回复试验。

图1 试验装置

1.4 应力松弛试验

棉样由两片不锈钢圆盘（不锈钢圆盘由丝杆和螺母组件固定，调节两片不锈钢圆盘的间距可获得不同应变的棉纤维）夹持进行松弛试验（室内温度19℃～25℃，相对湿度45%～57%），如图1（b）所示。薄膜压力传感器采集棉纤维内部压力值，每隔一定时间记录棉纤维压力值。棉纤维应变依次为76%、79%、81%、83%，分别进行应力松弛试验。

2 蠕变和松弛行为

棉纤维的蠕变回复曲线（施加20 N压力）如图2所示。

图2 棉纤维蠕变回复曲线

图2中，棉纤维的蠕变回复过程分为5个阶段，OA段为瞬时变形、AB段为减速蠕变（应变速率随时间增加而降低）、BC段为稳态蠕变（应变量趋于稳定）［10］、CD段为瞬时回复、DE段为缓慢回复。瞬间压力作用，纤维网快速屈曲变形，纤维间空隙减小，棉纤维展现出弹性。随着压力持续作用，棉纤维间不断滑移致密，其展现出黏弹性变形和黏塑性变形。各阶段应变依次定义为初始蠕变量εA、减 速 蠕 变量εBA（εBA=εB-εA）、稳态 蠕 变 量εCB（εCB=εC-εB）、急弹回复量εCD（εCD=εC-εD）、缓弹回复量εDE（εDE=εD-εE）和塑性蠕变量εE。

棉纤维的应力松弛曲线（应变为76%）如图3所示。图3中，棉纤维应力值随时间增加逐渐降低。

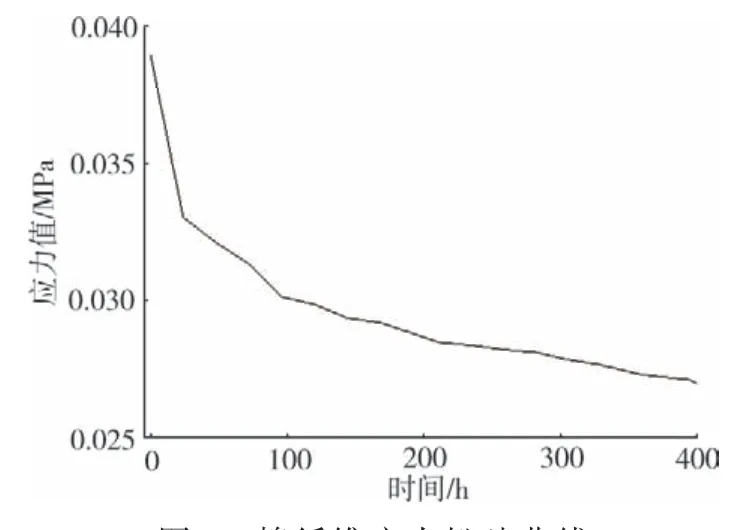
图3 棉纤维应力松弛曲线

3 黏弹性模型分析

棉纤维是高蓬松态的黏弹性材料，可通过弹簧和黏壶的组合表达其力学形态。黏弹性物料的蠕变多采用Burgers模型描述，本研究采用四元件模型模拟棉纤维的蠕变行为；黏弹性物料的应力松弛多采用Maxwell模型描述，本研究采用五元件模型模拟棉纤维的应力松弛行为。

3.1 蠕变回复模型

四元件模型如图4所示［11］。图4中E1、E2指弹簧的弹性模量，η1、η2指黏壶的黏滞系数。在外力作用下，弹簧E1瞬间响应，表征弹性变形；弹簧E2与黏壶η1并联逐渐响应，表征黏弹性变形；黏壶η2响应，表征塑性变形。

图4 四元件模型

四元件模型的蠕变回复方程可分别表示为式（1）和式（2）。

式中：ε为棉纤维蠕变应变（%）；ε′为棉纤维回复应变（%）；σ0为棉纤维应力（MPa）；t为蠕变回复时间（h）；t′为蠕变总时间（h），取值600 h。

四元件模型蠕变回复函数曲线如图5所示。

图5 四元件模型蠕变回复曲线

可以看出，四元件模型蠕变回复曲线与棉纤维的蠕变回复曲线（图2）基本一致，可较好表达棉纤维的蠕变行为。

3.2 应力松弛模型

五元件模型如图6所示［12］。图6中E0、E1、E2指弹簧的弹性模量，η1、η2指黏壶的黏滞系数。在外力作用下，材料应变ε0，弹簧E0、E1、E2瞬间响应，应力表征为ε0E0、ε0E1、ε0E2；与弹簧串联的黏壶η1和η2逐渐响应，应力逐渐下降。当松弛时间很长时，模型达到恒定应力ε0E0。

图6 五元件模型

五元件模型的应力松弛方程可表示为式（3）。

式中：ε0为棉纤维应变（%）；σ0为棉纤维应力（MPa）；t为应力松弛时间（h）。

五元件模型的应力松弛函数曲线如图7所示。其与棉纤维的应力松弛曲线（图3）相近，可较好表达棉纤维的应力松弛行为。

图7 五元件模型应力松弛曲线

4 模型参数确定

为了模拟计算棉纤维的力学参数，对其蠕变、回复、应力松弛的函数关系式进行简化。

蠕变过程，应变与时间的方程简化为式（4）。回复过程，应变与时间的方程简化为式（5）。

应力松弛过程，应变与时间的方程简化为式（6）。

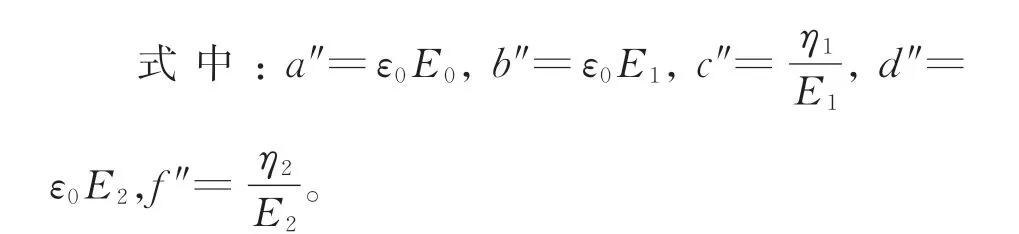
对图2蠕变回复过程、图3应力松弛过程试验条件下的应力和时间数据分别进行非线性曲线拟合，蠕变阶段拟合方程ε=32.350 1+0.014 2t-32.35exp（-t/0.003 8），相关系数R2=0.976 5；回复阶段拟合方程ε=5.160 2+22.286 exp［-（t-600）/6.999］，相关系数R2=0.921 8；应力松弛阶段拟合方程σ=0.072 3+8.133 73exp（-t/14.134 8）+8.133 73exp（-t/14.134 8），相关系数R2=0.999 8。可以看出相关系数R2均大于0.9，拟合效果较佳。非线性黏弹性模型能较好地表征棉纤维蠕变、回复、松弛过程，各过程分别对应的E0、E1、E2、η1、η2［13］，见表1。

表1 棉纤维蠕变、回复、应力松弛过程力学参数计算公式

5 棉纤维蠕变回复力学指标变化规律

图8为不同载荷作用下棉纤维压缩蠕变回复曲线，其应变指标见表2。

图8 不同载荷的棉纤维蠕变回复曲线

由表2可知，随着载荷增加，棉纤维的εA值增加，εBA值减少，εCB值趋于稳定，εCD值先减后增，εDE值呈增加趋势，εE值增加。载荷增加，棉纤维的急弹性变形增加，缓弹性变形减少；棉纤维弹性回复趋减，塑性变形积累增多。载荷越大，棉纤维内部结构越易于趋向致密态，棉纤维蠕变量越小，回复能力越弱。

表2 棉纤维蠕变回复过程的应变参数

棉纤维的蠕变回复力学指标见表3和表4。可以看出，随着载荷增加，棉纤维的蠕变回复力学指标均增大。表明棉纤维蠕变与回复力学曲线所表征的力学指标呈相似的变化规律，棉纤维蠕变与回复力学指标取决于棉纤维排布的紧密程度。载荷促使棉纤维内部结构由松散转致密。密度越高，棉纤维内部积累弹性能量越强，黏滞效应越明显。

表3 棉纤维蠕变力学指标

表4 棉纤维回复力学指标

6 蠕变量与棉纤维应力的关系

蠕变期间棉纤维内部传感器采集压力曲线如图9所示。

图9 蠕变过程棉纤维内部压力曲线

通过对比图8蠕变曲线与图9的压力曲线发现，随着蠕变量的增加，棉纤维内部应力亦增加。棉纤维的蠕变与应力数据进行线性拟合，拟合相关系数R2均大于0.9，拟合结果见表5。棉纤维的初始状态为松散、随机、各向异性排列，纤维与纤维之间项目搭接呈高空隙态结构。在蠕变压力作用下，棉纤维穿插、滑移、屈曲，不断调整形态，致使棉纤维结构致密。纤维网的致密化，强化了纤维网间力链分布密度概率，促使棉纤维接触压力传感器感应面的几率上升，薄膜压力传感器采集的压力亦不断增强。

表5 棉纤维内部采集应力与蠕变量关系

7 棉纤维应力松弛力学指标变化规律

图10为不同应变条件下棉纤维应力松弛曲线。压力传感器采集的棉纤维内应力随时间逐渐降低，表明压力促使纤维形变及纤维间滑移，棉纤维内部纤维结构调节，致使棉纤维内应力略有下降。应变量越高，棉纤维内应力越高。各应变条件下棉纤维应力松弛曲线变化规律相近，应力衰减量逐渐趋近于零，属于有限应力松弛。

图10 不同应变条件下棉纤维应力松弛曲线

棉纤维的应力松弛力学指标见表6。由表6可知，随着应变增加，棉纤维的应力松弛力学指标均增大。应变增大，棉纤维内部结构趋于致密，其存储的弹性性能、黏滞效应亦增强。

表6 棉纤维应力松弛力学指标

8 结论

（1）测试棉纤维的蠕变回复、应力松弛特性，棉纤维存在显著的蠕变变形、形变累积和应力松弛特征。

（2）基于黏弹性理论，对棉纤维的蠕变回复、应力松弛力学特征建立黏弹性力学模型。非线性黏弹性模型能较好地表征棉纤维的蠕变回复、应力松弛力学过程。

（3）随着载荷增加，棉纤维蠕变量与回复量均增加，棉纤维蠕变回复的力学指标E1、E2、η1、η2均增大。随着应变量增加，棉纤维内应力增加，棉纤维应力松弛的力学指标E0、E1、E2、η1、η2均增大。密度是决定棉纤维力学指标的关键因素。