随位移均匀变化的磁场中电磁感应规律的初探
甘恒一 胡 安 汤辰旭 姜付锦
(黄陂区第一中学 湖北 武汉 430030)
1 题目
如图1所示,在第一象限内存在垂直纸面向外的磁场,磁感应强度B=B0+kx,(B0>0,k>0且都是常数),x为某点到y轴的距离,有一个边长为L的正方形导体线框ABCD沿x轴从原点以速度v0匀速运动,求导体线框中产生的感应电动势E.
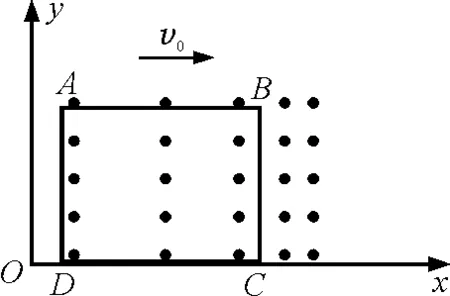
图1 题目题图
设AD所在位置坐标为xD,BC边所在位置为
xC,由法拉第电磁感应定律,则
EAD=BDLv0EBC=BCLv0xC-xD=L
导体线框中的总电动势为
E=BCLv0-BDLv0=L2kv0
2 若导体线框是正三角形会怎样
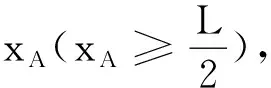
总电动势微元
把上式求定积分得

图2 导体线框边长为L的正三角形
3 若导体线框是一个半径为R的圆形,则结果又如何
如图3所示,在夹角为θ两边对称位置取微元Rdθ,则电动势微元为
dE=dE2-dE1=[B0+k(x0+Rsinθ)]Rv0·
sinθdθ-[B0+k(x0-Rsinθ)]Rv0sinθdθ
整理后得
dE=2RsinθkRv0sinθdθ=2R2kv0sin2θdθ
对以上式子求定积分得
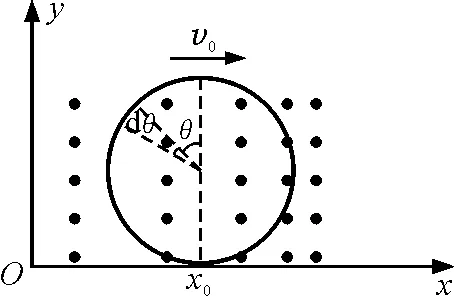
图3 导体线框为半径R的圆形
4 一点猜想
当导体线框是正方形时,导体线框中的总电动势为
E=BCLv0-BDLv0=L2kv0
当导体线框是正三角形时,导体线框中的总电动势为
当导体线框是圆形时,导体线框中的总电动势为
通过以上分析可以发现,感应电动势与导体线框的面积成正比,比例系数为kv0,为什么是这样的呢?
5 数学证明
如图4所示,假设导体线框是任意形状的封闭曲线,把曲线在纵向平均分割成无数个条状面元,每个面元的高度为Δy,在其上任意选择一个矩形ABCD,则这个矩形中产生的感应电动势为
dE=(B0+kxD)v0Δy-(B0+kxA)v0Δy=
v0k(xD-xA)Δy=v0kΔxΔy
上式中的ΔyΔx正好是面元的面积,所以对它求定积分后就是导体线框的面积.
综上所述,在随位移均匀变化的磁场中,导体线框在匀速运动时产生的 感应电动势与导体线框的面积成正比,比例系数为kv0.

图4 导体线框为任意形状的封闭曲线

