一种基于Kd-tree 射线追踪法的卫星RCS 预估方法

肇 格,张 军,胡杰民

(国防科技大学ATR国防科技重点实验室,长沙410073)

1 引 言

低频方法在雷达散射截面(RCS)的计算上有着很大的局限性,特别是对于电大尺寸具有复杂结构的目标,该方法往往是行不通的。而对于普通的高频方法,例如物理光学方法,由于其是建立在很多种近似上的,所以在计算很多问题时很难达到准确性的要求。射线追踪与物理光学(PO)相结合的方法包含了散射场中多次散射的高阶项,是计算具有多次散射效应目标RCS 的一种有效方法,其有效性已经得到了大量的验证[1-3]。但这种方法也只被用在了角反射器的计算上。

根据卫星目标的三维面元模型建立起来的Kd-tree 是一种根据k 维空间中的点集对空间进行分割的数据结构,常用于范围查找和最近邻查找等,是一种特殊的二叉空间分割树[4-5]。文献[5]中作者将其用于射线追踪方法使得对于射线的追踪效率大大提高。本文将Kd-tree 方法应用于射线追踪,仿真结果表明该方法在计算效率方面达到了良好的效果,结合PO 方法就可以得到给定模型的RCS 预估值。计算结果表明,结合了Kd-tree 和射线追踪的方法可以有效地计算复杂电大尺寸空间目标的RCS预估值。

2 卫星目标模型的剖分原则

卫星目标模型建好之后,将其剖分成小的三角面元,具体的剖分应当遵循以下原则:假定每个小面元都只有被照射和未被照射两种情况。因此,为了比较准确地反映多次散射的情况,剖分时每个面元都不能太大,以使最小结构都能被面元模型很好地描述。在满足上述条件下,为了提高计算精度,这里采用九点插值方法对每一面元的物理光学积分进行计算。

3 Kd-tree 结构的建立

Kd-tree 结构是自上而下以一种递归的方式构造的,其中根节点对应于包含了目标所有面元的长方体包围盒。然后长方体包围盒按一个轴方向被分割平面分成两个子长方体,组织成一个二叉树,即一个根节点被分成了两个内节点。剖分平面是选择使射线与面元相交概率最大的平面,且该平面可以是垂直于x 、y 、z 轴的任何一个平面。若某一子长方体包围盒中所含的面元数大于给定的值,且Kd -tree 的深度小于给定的深度,则需对该子包围盒进一步剖分。上述剖分过程递归地进行,直至Kd -tree 的每一个叶子节点所对应的子空间所包含的面元数小于给定的值或该Kd-tree 的深度大于给定的深度为止。另外,如果分割过程中面元与分割平面相交,则使面元分别属于两个相应的节点。Kd-tree建立之后,还需使每一叶子节点对应的包围盒的6个面与其他内节点,叶子节点或空节点建立指向关系,具体细节可以参见文献[4] 。Kd-tree 的建立可以大大减小反射线追踪时从Kd-tree 自上而下的追踪过程。二维的Kd-tree 如图1 所示。

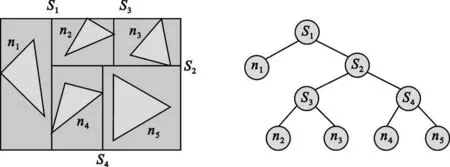
图1 二维Kd-tree 模型Fig.1 The two-dimensional model of Kd-tree

4 PO 积分与路径的射线追踪

4.1 应用物理光学积分计算每一面元一阶等效电流对于远区散射场的贡献

本文所介绍的方法是以面元为单位进行的,即计算出每一面元各阶等效电流对于远区散射场的贡献,然后将所有面元的贡献相加即可得总的远区散射场。其中,每一面元对于远区散射场的贡献可用物理光学积分表示为

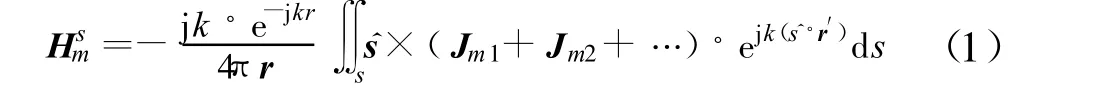
其中,Hsm为面元m 对于远区散射场的贡献,Jm1、Jm2等为面元m 上的一阶、二阶和更高阶电流。

应用切平面近似,面元m 上的一阶等效电流可表示为

其中, m 为面元m 的法向矢量, Hi为面元m 处的磁场强度。

4.2 根据入射波判断初次入射明暗面

该步骤需对所有面元一一进行判断,判断其是否被入射波直接照射到。判断某一面元m 是否被入射波照射到的方法如下。

设入射波矢量为 i,面元m 的法向矢量为 n ,则m 面元被入射波照亮应满足以下两个条件:

(1)入射波矢量为 i 与面元m 的法向矢量为 m(mx,my,mz)满足: i × m ≤0;

(2)入射波照射到面元m 的过程未被其他面元遮挡。

其中,条件2 的判断方法如下:

设面元中心点坐标rm(xm, ym,zm),入射波矢量 i(ix,iy,iz),该面元上的入射线方程为

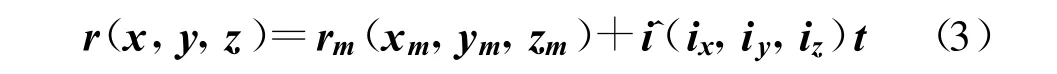
将该直线方程与其他面元逐一进行判断,如果该直线方程与其他所有面元无交点,则面元m 未被其他面元遮挡,即面元m 被入射波直接照射到,否则面元m 在入射波照射过程被其他面元遮挡,未被入射波直接照射到。

以面元n 为例,判断式(3)直线与面元n 是否有交点的方法如下。

设面元n 的中心点坐标为rn(xn, yn,zn),面元法向矢量为 n(nx, ny,nz),则该面元所在的平面可表示为

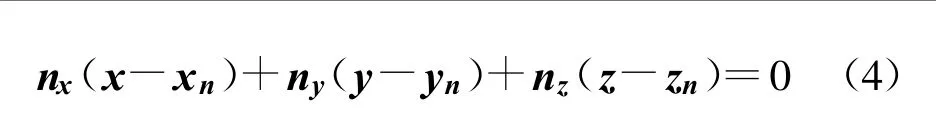
联立式(3)与式(4)可求得式(3)直线与面元n所在平面的交点P(x0,y0,z0)。这里:

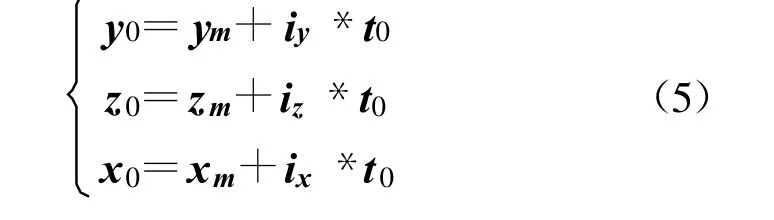
其中:

t0=[ nx(xn-xm)+ny(yn-ym)+nz(zn-zm)]/[ nx·ix +ny·i y+nz·iz] 。

因为我们判断的是射线到达面元m 之前的情况,所以t 0应该小于0。此时,如果该交点P(x0,y0,z0)在面元n 内,则式(3)与面元n 有交点,否则式(3)与面元n 无交点。判断一点P(x0, y0,z0)是否在三角形面元n 内的方法如下:

3 个顶点N1、N2、N3与面元n 的法向矢量n (nx,ny,nz)成右手螺旋法则的顺序排列,如图2 所示,则P 点位于面元n 内部的充要条件是式(6)中的3 个式同时满足。

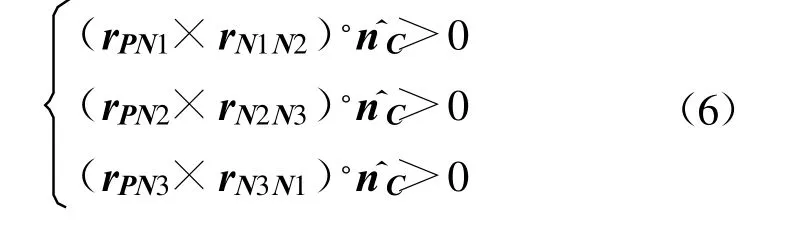
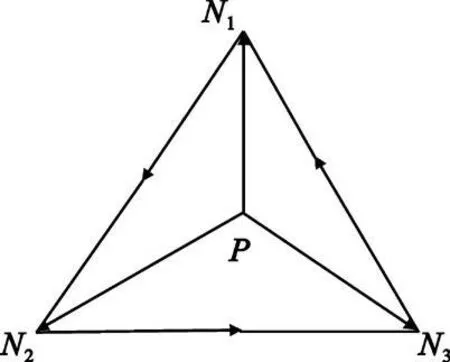
图2 射线与面元相交判断Fig.2 Intersect judge of ray and surface

4.3 面元处二阶等效电流对远区散射场的贡献的计算

仍以经面元n 反射的反射线照亮面元m 为例。面元n 处的入射场可表示为

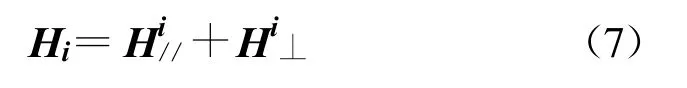
则经面元n 反射的反射场可表示为

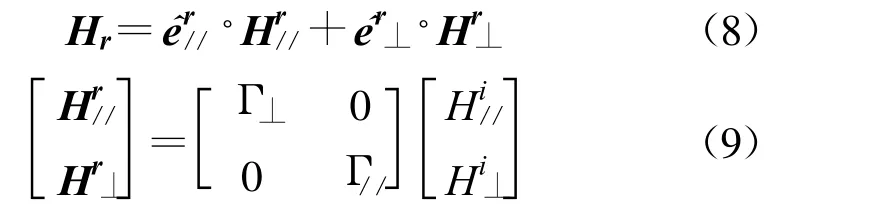
其中,Hi// = e//·Hi,Hi⊥= e ⊥·Hi, e ⊥= i × n, e// = i× e⊥, er//= k × e⊥, Γ//和Γ⊥分别为平行极化和垂直极化的反射系数。

5 仿真结果

算例1:三面角反射器是验证高频多次弹跳散射的标准[6]。这里所取的三面角反射器中直角三角形的直角边长为1 m,如图3 所示。θ在φ=45°的平面从0°到90°变化,入射波频率为6 GHz,VV 极化。

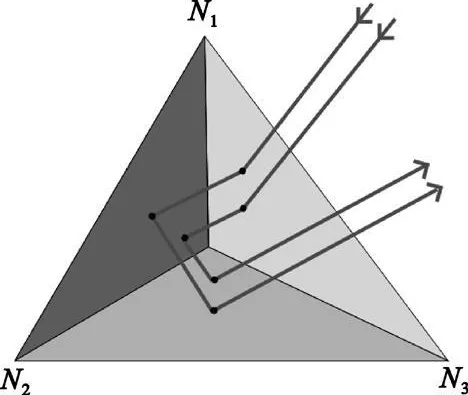
图3 三面角反射器Fig.3 Three sides of corner reflectors

图4 给出了三面角反射器的后向散射系数,并将其与MoM 方法的结果进行了比较。从图中可以看出,本文所提出的方法与MoM 方法所得的结果符合得很好。在计算效率方面,MoM 方法耗时超过24 h,而本文所提出的方法计算所有90 个角度用时5 min。

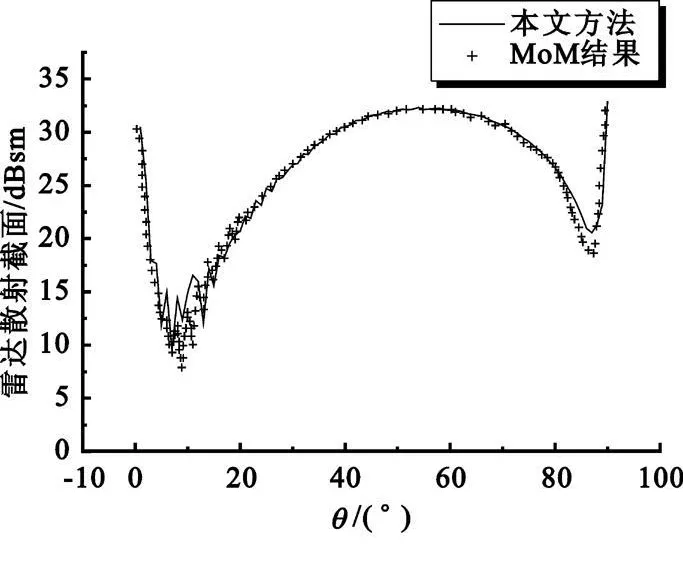
图4 本文方法与MoM 方法结果比较Fig.4 Comparison between the proposed method and the MoM

算例2:将该方法应用于卫星目标的计算。卫星模型如图5 所示,在模型上面的平台上为一天线面结构,该天线面结构中有圆柱和方体结构,模型被剖分为29 569个面元。入射波频率为3 GHz,VV 极化。

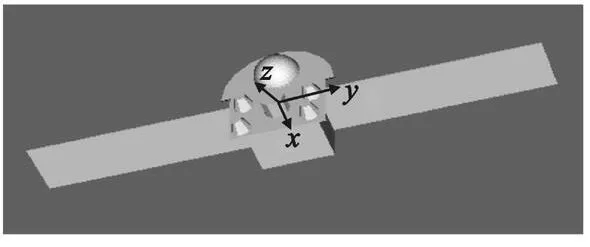
图5 卫星模型Fig.5 Satellite model

图6 给出了本文方法所得结果与实验结果和单纯PO 方法所得结果的比较。从图中我们可以看出,单纯的PO 方法结果与实验结果相差很大,这表明对于卫星天线面这种复杂结构,各部分之间多次散射的效应十分明显,而单纯的PO 方法未能包含这种效应。本文的改进方法则能有效涵盖这种多次散射效应,所以与实验结果符合得比较好。

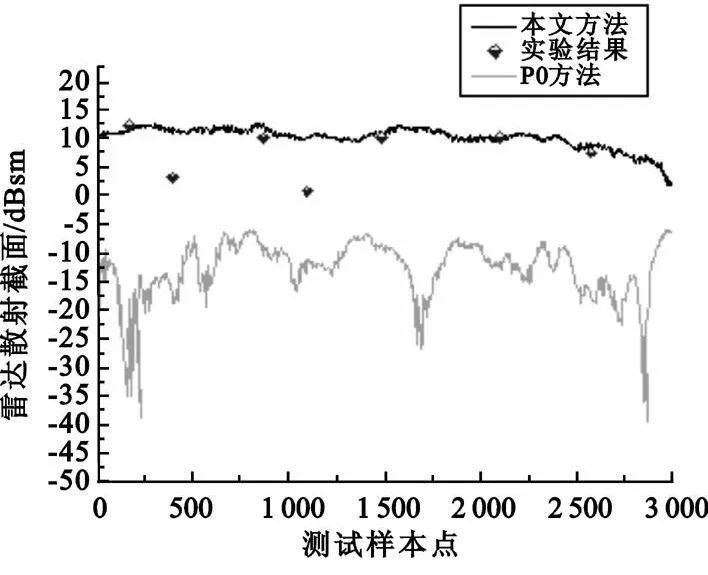
图6 卫星RCS 计算结果比较Fig.6 Comparison of satellite RCS calculation

6 结 论

本文提供了一种将PO 方法与Kd-tree 空间分割方法及射线追踪相结合的改进方法。该方法因为有效地计入了目标各部分之间的多次散射效应,且为一种高频方法,所以对于计算电大尺寸具有较强耦合效应的复杂目标是非常行之有效的。为了方便起见,本文没有考虑边缘绕射效应所产生的影响,如果用物理绕射理论(PTD)对之加以修正,可能会得到更令人满意的结果。值得一提的是,其他大多数方法的计算量会随着入射波频率的增大而显著增加,而本文方法的计算量则不会受到入射波频率的影响,这使得该方法在高频散射计算时更能显示出更多的优势。

[1] Knott E F.RCS reduction of dihedral corners[ J] .IEEE Transactions on Antennas and Propagation,1977, 25(3):406-409.

[2] Ross R A.Application of geometrical diffraction theory to reflex scattering centers[C]//Proceedings of 1968 IEEE International Symposium on Antennas and Propagation.Monterey,CA:IEEE,1968:94-99.

[3] Anderson W C.Consequence of nonorthogonality on the scattering properties of dihedral reflectors[ J] .IEEE Transactions on Antennas and Propagation, 1987,35(10):1154-1159.

[4] Havran V.Heuristic Ray Shooting Algorithm[D] .Prague:University Czech Technical, 2000.

[5] Tao Y B, Lin H, Bao H J.Kd-tree based fast ray tracing for RCS prediction[ J] .Progress in Electromagnetics Research, 2008, 81:329-341.

[6] Baldauf J, Lee S W, Lin L, et al.High frequency scattering from trihedral corner reflectors and other benchmark targets:SBR vs.experiments[ J] .IEEE Transactions on Antennas and Propagation, 1991,39(9):1345-1351.

[7] Tao Y B, Lin H, Bao H J.GPU-based shooting and bouncing ray method for fast RCS prediction[J] .IEEE Transactions on Antennas and Propagation,2010,58(2):494-502.