基于PSO-BP神经网络的DOA估计方法✴

孟非，王旭

基于PSO-BP神经网络的DOA估计方法✴

孟非，王旭

（江苏科技大学电子信息学院，江苏镇江212003）

提出利用粒子群算法优化BP神经网络来改善来波到达角估计性能的方法。传统的BP神经网络易陷入局部最优，因此采用粒子群算法对网络的权值和阈值进行优化，并将其应用到来波到达角估计中。所提方法仅利用阵列协方差矩阵的第一行作为来波方位特征，与常用的协方差矩阵上三角特征相比，在不损失有效方位信息的基础上使特征维数极大降低。仿真实验证明：同经典的RBF神经网络方法相比，基于所提方法的神经网络结构更简洁，泛化性能更好，来波方位估计精度更高。

波达角估计；粒子群算法；神经网络；特征维数

1 引言

在无源定位、声纳阵列测向、地震和地质资源探测以及移动通信等诸多研究领域，来波信号到达角估计问题是一个热点问题［1］。在过去的几十年中，一些高性能和高分辨率的算法得到了重大发展，如传统的MUSIC算法、ESPRIT算法等。尽管它们提供了合理有效的估计，但是需要进行大量的计算，进而消耗大量的时间，不能达到实时性的要求。

随着计算智能技术的飞速发展，人们开始研究通过学习大量的样本来解决来波到达角估计问题，而神经络无疑被人们认为是解决这一问题的强有力工具。神经网络因其非线性映射及泛化能力可以用于来波到达角估计问题，其优点在于建模过程是采用训练样本构造神经网络，而不再是精确的数学方程式，在实际情况下采集到的训练样本可以将噪声、信号模型、信噪比、传输通道等因素考虑进去，而无需进行特征值分解、谱峰搜索，且计算可以并行快速实现，从而有望应用到实际工程。文献［2-6］采用了RBF神经网络来解决来波到达角估计问题，无论在估计精度和估计时间上都优于MUSIC算法［7］。

BP神经网络也能够解决DOA估计问题，但BP算法容易陷入局部最小点，不能够很好地得到理想的效果。本文首先运用粒子群算法来优化BP神经网络的权阈值，然后再用BP算法对神经网络进行训练，以达到寻找全局最小值的目的；其次，仅利用阵列协方差矩阵的第一行作为来波方位特征，与常用的协方差矩阵上三角特征相比，在不损失有效方位信息的基础上使特征维数极大降低，大大简化了DOA估计模型中神经网络的输入维数。同RBF神经网络相比，本文方法在处理DOA估计问题时具有更好的精确度。

2 PSO-BP神经网络

2.1粒子群算法的简单介绍

PSO算法是一种基于群体智能的进化算法［8］，其思想来源于人工生命和进化计算理论，最早是受鸟群觅食行为的启发提出的。PSO算法采用实数求解，并且需要调整的参数较少，易于实现，是一种通用的全局搜索算法。它的优势在于简单容易实现，同时又有深刻的智能背景，既适合科学研究，又特别适合工程应用。PSO算法的基本公式如下：

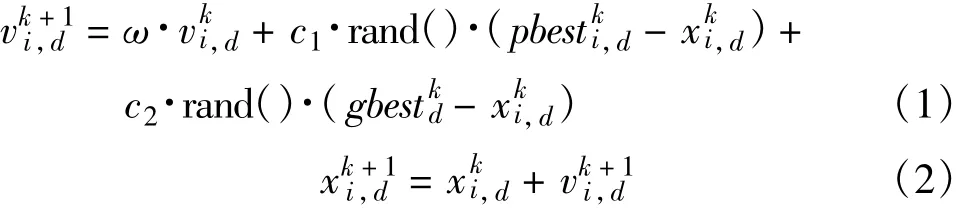
式中，ω为惯性权重；c1和c2被称为学习因子；rand（）为介于（0，1）的随机数，这几个参数决定了粒子群优化的开发能力和探测能力分别为粒子i在第k次迭代中第d维的速度和位置，两者均被限制在一定的范围内；pbest为粒子i在第d维的个体极值的位置；gbes为群体在第d维的全局极值的位置。

2.2PSO-BP组合模型核心思想

BP算法是由信号的正向传播和误差的反向传播两个过程组成，正向传播时，输入样本从输入层传入，然后经各隐层处理后传向输出层。如果输出层的实际输入与期望输出不相符，则将转到误差的反向传播阶段。误差反传是将输出误差以某种形式通过隐层向输入层逐层反传，并将误差分摊给各层的所有单元，从而获得各层单元的误差信号，此误差信号即作为修正各单元权阈值的依据。这种信号正向传播与误差反向传播的权阈值调整过程是周而复始地进行的。权阈值不断调整过程就是网络的学习训练过程，直至训练网络输出达到预期的要求为止。

从BP算法的整个学习过程可以看出，其在学习过程中没有引入任何额外参数，其学习过程完全是根据训练样本对初始权阈值的调整，所以最初权阈值选取的好坏将会直接影响到最终模型的泛化能力。最近的研究表明，对BP模型的初始权阈值首先采用一定的方法进行优化，然后再采用BP算法进行二次优化确定权阈值，最终可以有效提高模型的运行效率。因此，本文在事先已经确定好的BP

神经网络模型基础上，将粒子群优化算法与BP算法结合，采用粒子群算法寻找神经网络的初始权值与阈值，接着再采用改进的BP神经网络算法来训练经过粒子群算法寻优的初始权值与阈值，得到模型最终的权值与阈值，从而形成最终模型。利用此种方法构造的模型可以有效地克服单纯BP神经网络学习稳定性差、可靠性低与易陷入局部极小等问题。

采用PSO-BP组合算法模型对信号来波到达角进行预测的步骤如下。

（1）确定粒子群规模，即粒子的个数m和维数n。本文选取粒子的个数为m=50，假设神经网络模型结构为M-N-2，则粒子的维数n=（M+N）×

N+（N+1）×2。

（2）学习因子c1和c2以及惯性权重ω的确定。学习因子决定了粒子群优化的开发能力和探测能力，本文中取c1=c2=2。惯性权重ω用来控制粒子以前速度对当前速度的影响，它将影响粒子的全局搜索能力和局部搜索能力，为使粒子保持运动惯性，使其有能力探索新的区域，本文采取线性递减权值策略，如式（3）所示：

式中，Tmax为最大进化代数，t为当前进化代数，w0为初始惯性权值，wend为迭代至最大代数时的惯性权值。其中w0=0.95，wend=0.4，Tmax=500。

（3）确定适应度函数。以训练均方误差函数E作为粒子的适应度评价函数，即：

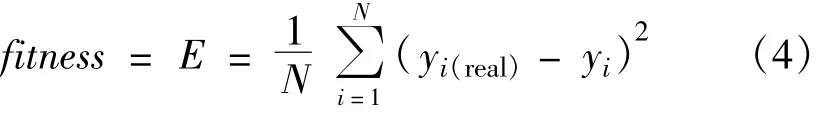
式中，N为训练的样本数，yi（real）为第i个样本的实际值，yi为第i个样本的模型输出值。因此，算法迭代停止时适应度最低的粒子对应的位置，即为问题所求的最优解。

（4）更新粒子的位置与速度，计算出算法的误差。

（5）判断误差是否满足预设精度或迭代是否达到最大次数。若误差满足预设精度，算法收敛，最后一次迭代的全局最优值中每一维的权值和阈值就是所求的最优解；若迭代次数未达到最大，返回步骤4，算法继续迭代，否则算法终止。

（6）以粒子群算法优化得到的权值和阈值作为网络初始值，利用BP算法训练神经网络达到指定精度，以此建立DOA估计的预测模型。

3 DOA估计模型

假设有M个天线组成的均匀线性阵列，K个非相干的窄带信号源以｛θ1θ2…θK｝的角度入射到天线阵列上，利用波的传播过程的关系，则第i个天线阵元接收到的信号可表示为

其中，sm是第m个窄带信号，ni（t）是第i个天线阵元接收到的噪声，ω0是信号源中心频率，d为天线阵元之间的间距，c是光速。将式（3）以矩阵的方式表示出来：

其中，A是M×K的信号导向矩阵。

假设噪声信号是独立于窄带信号S（t）的均值为0、方差为σ2的高斯白噪声，那么接收信号的空间关联矩阵R可表示如下：

在这里需要对神经网络的输入进行改变，多数文献中神经网络的输入为协方差矩阵的上（下）三角矩阵，而本文中神经网络的输入只取协方差矩阵的第一行，具体原因如下：假设忽略每个协方差矩阵上面的噪声，任意两个阵元的协方差可表示为

其中Xi（t）=αiS（t）Xl（t）=αlS（t），那么

在这里，定义P=E｛S（t）S（t）H｝，那么Pil= E｛Si（t）Sl（t）*｝，其中*代表复共轭。因此，当所接收的信号源互为非相干时，那么

如果式（17）可以写成如下形式：αPαHβPγH= βPαHαPγH，则公式（15）就可以变为

从公式（18）中可以看到，当接收信号源互为非相干时，协方差矩阵的第一行足以代表整个协方差矩阵的所有信息，因此，本文只取协方差矩阵的第一行作为每个样本的神经网络的输入，即神经网络的特征输入维数为2M-1个。基于神经网络的DOA估计框图如图1所示。

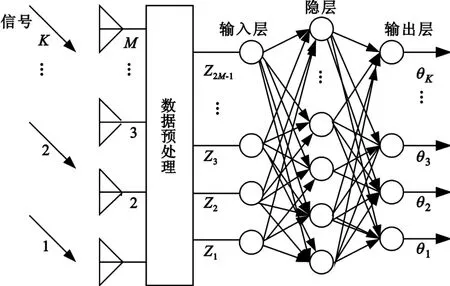
图1 基于神经网络的DOA估计框图Fig.1 Block diagram of DOA estimation based on NN

4 仿真实验

4.1仿真实验1

仿真条件：天线阵元个数M为5，两个非相干的正弦信号源，信噪比为10 dB，快拍数为500，阵元间距为半波长。那么，以大多数文献中采用的RBF神经网络方法，神经网络的输入个数为2M（M-1），即为40个，而按照本文的方法，神经网络的输入个数为2M-1，即为9个，这样大大减少了神经网络结构的复杂度。

训练样本：两个信号源的间隔为20°和25°；测试样本：两个信号源间隔为22°。以间隔20°为例，也就是说，当第一个信号源为-90°时，第二个信号源为-70°；第一个信号源为-89°时，第二个信号源为-69°，以此类推，覆盖整个［-90°～90°］范围。另外，RBF方法中采用的隐层神经元个数为40个，而本方法中采用的隐层神经元个数仅为10个。图2和图3给出了RBF方法在处理DOA估计时的输出预测曲线和误差曲线，图4和图5分别给出了本文方法在处理DOA估计的输出预测曲线和误差曲线。

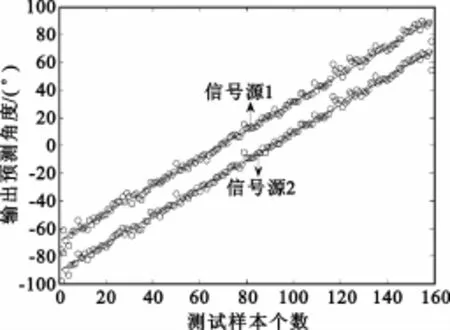
图2 基于RBFNN的DOA估计输出预测曲线Fig.2 The forecast error curve of DOA estimation based on RBFNN

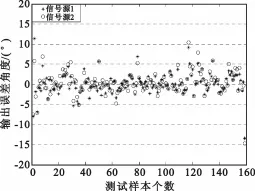
图3 基于RBFNN的DOA估计输出误差曲线Fig.3 The output error curve of DOA estimation based on RBFNN

图4 基于PSO-BPNN的DOA估计输出预测曲线Fig.4 The forecast error curve of DOA estimation based on PSO-BPNN

图5 基于PSO-BPNN的DOA估计输出误差曲线Fig.5 The output error curve of DOA estimation based on PSO-BPNN

从上述图中可以看出，尽管PSO-BP神经网络的隐层神经元的个数仅仅是RBF神经网络的一半，但与RBF神经网络相比，本文方法的精确度更高。

4.2仿真实验2

考察不同信噪比对DOA估计性能的影响。仿真条件：在上述两种方法的基础上，天线阵元M= 10，信号源N=2，快拍数L=500。

训练样本：两信号源间隔为10°和15°；测试样本：两信号源间隔为12°。依次估计上述条件两种方法在信噪比为-5 dB、0 dB、5 dB、10 dB、15 dB、20 dB、25 dB下的均方误差。具体仿真结果如图6所示。从图6中可以看到：随着信噪比的增大，均方误差逐渐减小，-5～15 dB之间，MSE变化得比较大；15 dB以后，MSE逐渐趋于平稳，在低信噪比下，本文方法的处理效果明显好于RBF神经网络的处理效果。

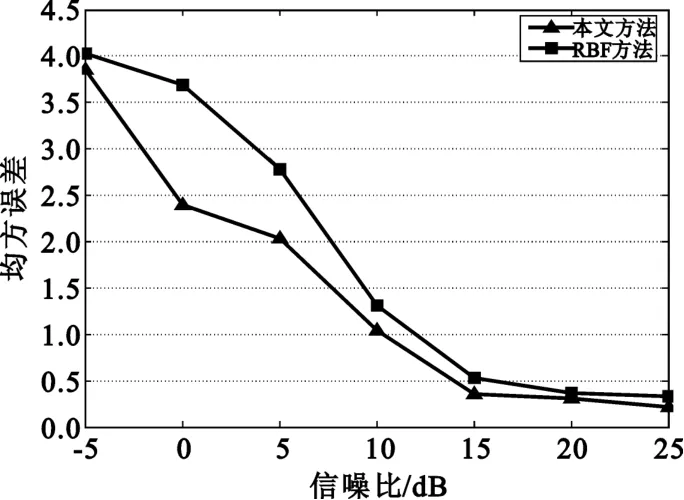
图6 不同信噪比下两种方法的均方误差Fig.6 The MSE of two methods in different SNRs

5 结论

本文主要利用粒子群算法优化BP神经网络来解决DOA估计问题。本文在用PSO-BP神经网络解决DOA估计问题时，神经网络的结构复杂度大大降低，从而提高了神经网络的预测精度。一方面，PSO-BP神经网络的输入仅取协方差矩阵的第一行，减少了神经网络的输入特征维数；另一方面，PSO-BP神经网络所需隐层神经元个数大大少于RBF神经网络所采用的个数。另外，本文方法的唯一缺点是，运用粒子群算法训练BP算法需要花费一定量的时间（约15 min），但训练是离线的，并不影响DOA估计的实时性。因此，利用本文方法处理DOA估计问题具有更好的优越性。

［1］Li Bai，Peng C Y，Biswas S.Association of DOA Estimation from Two ULAs［J］.IEEE Transactions on Instrumentation and Measurement，2008，57（6）：1094-1101.

［2］Zooghby A H，Christotodoulou C G.Performance of Radial-Basis Function Networks for Direction of Arrival Estimation with Antenna Arrays［J］.IEEE Transactions on Antennas and Propagation，1997，45（11）：1611-1617.

［3］Zooghby A H，Christotodoulou C G.A Neural Network-Based Smart Antenna for Multiple Source Tracking［J］.IEEE Transactions on Antennas and Propagation，2000，48（5）：768 -776.

［4］Vigneshwaran S，Sundararajan N.Direction of Arrival Estimation Under Array Sensor Failures Using a Minimal Resource Allocation Neural Network［J］.IEEE Transactions on Antennas and Propagation，2007，55（2）：334-343.

［5］张旻，李鹏飞.基于分层神经网络的宽频段DOA估计方法［J］.电子与信息学报，2009，31（9）：2118-2122.

ZHANG Min，LI Peng-fei.A Broadband Direction of Arrival Estimation Approach Based on Hirearchy Neural Networks［J］.Journal of Electronics and Information Technology，2009，31（9）：2118-2122.（in Chinese）

［6］Kuwahra Matsumoto.Experiments of direction finder by RBF neural network with postprocessing［J］.IEEE Electronic Letters，2005，41（10）：24-25.

［7］卢新文.基于提升小波算子的MUSIC法的DOA估计［J］.电讯技术，2010，50（12）：33-38.

LU Xin-wen.DOA Estimation with Music Algorithm Based on Lifting Wavelet Operator［J］.Telecommunication Engineering，2010，50（12）：33-38.（in Chinese）

［8］Kennedy J，Eberhart R.Particle Swarm Optimization［C］／／Proceedings of 1995 IEEE International Conference on Neural Networks.Perth，Australia：IEEE，1995：1942-1948.

MENG Fei was born in Shenyang，Liaoning Province，in 1977.She is now a lecturer.Her research concerns computational intelligence technologies and its applications.

王旭（1986—），男，河南洛阳人，2009年获学士学位，现为硕士研究生，主要研究方向为阵列信号处理技术。

WANG Xu was born in Luoyang，Henan Province，in 1986.He received the B.S.degree in 2009.He is now a graduate student. His research direction is array signal processing.

Email：andyluck1234＠126.com

DOA Estimation Method Based on PSO-BP Neural Network

MENG Fei，WANG Xu
（School of Electronics and Information，Jiangsu University of Science and Technology，Zhenjiang 212003，China）

Particle swarm optimization（PSO）is used for optimization of BP neural network to improve the performance of direction of arrival（DOA）estimation.Due to the fact that BP neural network is inclined to be trapped in local minimum point，a novel network-PSO based BP neural network is proposed and applied to DOA estimation.This method uses the first row of correlation matrix instead of commonly used upper triangular half of the covariance matrix，therefore the feature dimension is largely reduced without losing any DOA information.Experimental results show that the performance of the proposed method is much better than that of classic RBF method in terms of neural network size，generalization and estimation precision.

DOA estimation；particle swarm optimization；neural network；feature dimension

The National Defense Science and Technology Pre-research Program（10J3.5.2）

TN911.72

A

10.3969／j.issn.1001-893x.2012.05.018

孟非（1977-），女，辽宁沈阳人，讲师，主要研究方向为计算智能技术及其应用；

1001-893X（2012）05-0694-05

2011-10-15；

2012-02-22

国防科技预研项目（10J3.5.2）