对机械波半波损失现象的物理解释

李存志

(西安电子科技大学 物理与光电工程学院，陕西 西安 710071)

机械波的半波损失现象早已被证明［1－3］，不过证明过程均是利用数学方法，证明过程也并不复杂。尽管如此，人们对半波损失现象仍感到困惑，或者说人们承认对半波损失现象的数学解释，但在物理上并未完全接受。本文则试图用物理方法解释半波损失现象。

如图1 所示，平面简谐波垂直入射到两种介质分界面，将引起波的反射和透射。设入射波、反射波和透射波波函数分别为

图1 平面简谐波垂直入射到两种介质分界面示意图

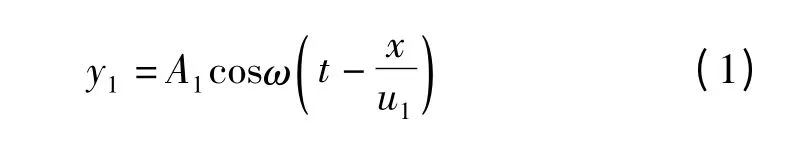
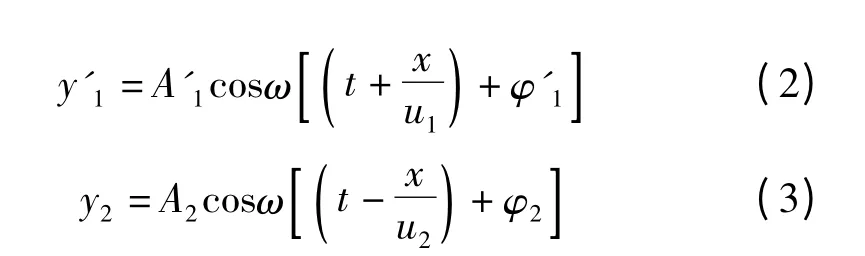
式中，φ'1和φ2分别为x=0 处反射波和透射波相对于入射波的相位差，u1和u2分别为波在两种介质中的传播速度。

在分界面上(x=0 处)的边界条件为

(1)位移连续，即

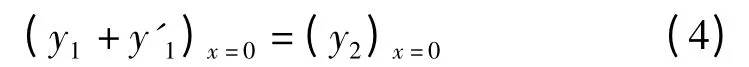
(2)应力连续，以纵波为例，有

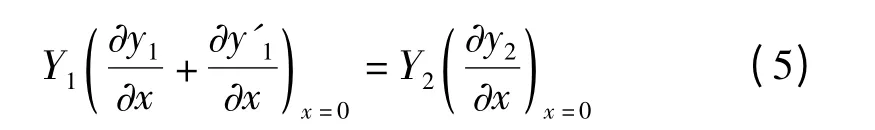
式中，Y1和Y2分别为两种介质的杨氏弹性模量。

通常，将式(1)、式(2)和式(3)代入式(4)和式(5)用数学方法证明半波损失现象。

1 用物理方法解释半波损失现象

由式(1)、式(2)、式(3)、式(4)和式(5)可得出如下推论:

推论1 界面两侧质元具有相同的振动位移、速度和加速度。

推论2 对于同一质元，入射波引起的应变和入射波引起的振动速度反相。

这是因为

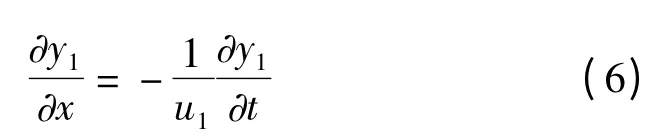
同样可证明，反射波引起的应变和反射波引起的振动速度同相，透射波引起的应变和透射波引起的振动速度反相。

推论3 界面两侧质元的应变同相。

推论4 入射波的平均能流密度减去反射波的平均能流密度等于透射波的平均能流密度。

证明 将式(1)、式(2)、式(3)代入式(4)并对时间t 求导得

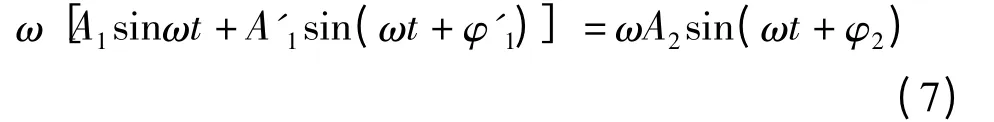
将式(1)、式(2)、式(3)代入式(5)并利用u1=得

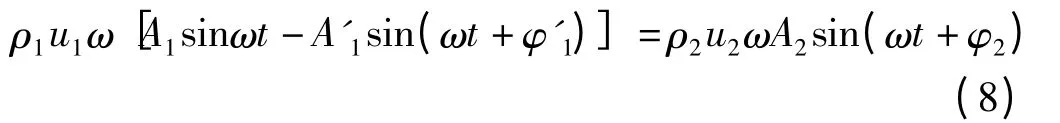
将式(7)和式(8)相乘并在波的一个周期内对时间求平均得

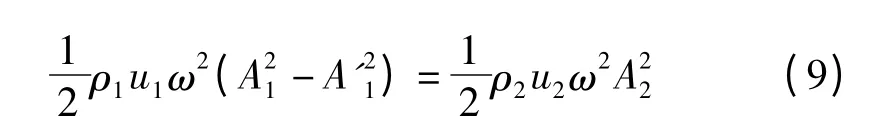
式中，ρ1和ρ2分别为两种介质的密度。式(9)正是波的能量守恒方程，可证明此方程对于机械波在固定端和自由端反射时亦成立。

由上述4 个推论可证明如下结论:

结论1 在界面处，反射波与透射波和入射波或者同相或者反相。

证明在界面处，假设在某时刻入射波在正向最大位移处，则在该时刻入射波引起的振动速度和应变应当为零。若此刻反射波和透射波引起的位移不在正向或负向最大位移处，则反射波和透射波引起的振动速度就应当不为零。根据推论1 和推论2，反射波和透射波引起的振动速度应当相等，因而反射波和透射波引起的应变应当相差一负号，这和推论3 相矛盾，即此刻反射波和透射波引起的位移只能在正向或负向最大位移处，结论得证。

结论2 在界面处，透射波和入射波同相。

证明 根据式(9)，反射波的振幅A'1小于入射波的振幅A1，因此在界面处无论反射波与入射波同相还是反相，入射波一侧质元的合振动应当与入射波引起的振动同相，根据推论1，在界面处透射波与入射波同相。

结论3 当入射波由波密媒质进入波疏媒质时，在界面处反射波和入射波同相。

证明当入射波由波密媒质进入波疏媒质时，假设在界面处反射波与入射波反相，根据推论1，应有

将式(10)代入式(9)得

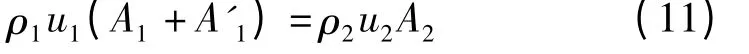
由于ρ1u1＞ρ2u2，根据式(11)有

上式与式(10)相矛盾，结论得证。

结论4 当入射波由波疏媒质进入波密媒质时，在界面处反射波和入射波反相。

证明 当入射波由波疏媒质进入波密媒质时，假设在界面处反射波与入射波同相，根据推论1，应有

将式(13)代入式(9)得

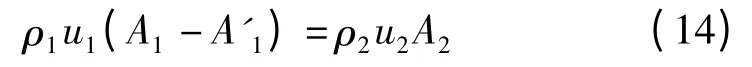
由于ρ1u1＜ρ2u2，根据式(14)有

上式与式(13)相矛盾，结论得证。

结论5 对于固定端，边界条件式(5)失效，式(4)变为

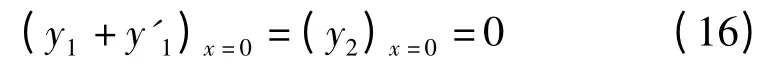
即界面处位移连续且始终为零。

根据上式，透射波的振幅A2=0，即对于这情况没有透射波，由式(9)得

即反射波的振幅等于入射波的振幅。反射波与入射波相干叠加形成驻波，为了保证界面处质元合振动位移始终为零，界面处应为波节(合振动振幅为零)，从而在界面处反射波与入射波反相。

对于固定端，边界条件式(5)失效，而应当以下面的应力条件代替式(5)

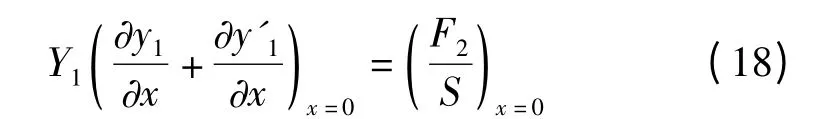
结论6 对于自由端，边界条件式(4)失效，式(5)变为

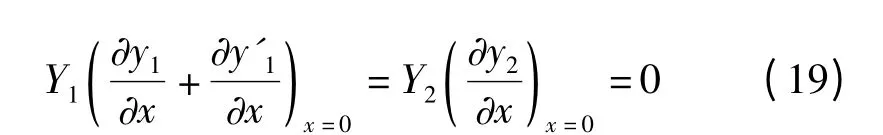
即界面处应力连续且始终为零。

根据上式，透射波的振幅A2=0，即对于这种情况亦没有透射波，由式(9)得

即反射波的振幅等于入射波的振幅。反射波与入射波相干叠加形成驻波，为了保证界面处应力始终为零，界面处应为波腹(应变始终为零)，从而在界面处反射波与入射波同相。

3 结束语

根据界面处的边界条件，利用物理方法解释了机械波的半波损失现象，对半波损失现象的理解有了一个较为清晰的物理图像。

［1］ 程守洙，江之永.普通物理学［M］.北京:高等教育出版社，1999.

［2］ 刘启能.产生半波损失的条件究竟是什么［J］.大学物理，2000，19(6):14－15.

［3］ 刘志强.机械波半波损失的证明［J］.大理学院学报，2010，9(4):57－58.