半波带法研究夫琅禾费单缝衍射的局限性分析*

董 鹏 张立红

[中国石油大学(华东)理学院基础物理系 山东 青岛 266580]

1 引言

在大学物理课程中，对于夫琅禾费单缝衍射这一内容，一般采用两种方法展开研究，一是积分法，即利用菲涅耳衍射积分公式严格求解衍射光强，从而全面了解单缝衍射的光强分布规律；二是半波带法，即通过半波带法定性分析明暗条纹出现的衍射角条件，从而获取衍射图样的主要特征．积分法由于计算复杂一般作为选学内容，或者仅对方法作简单介绍并直接给出计算结果，而对计算过程不作详细研究．半波带法因构思巧妙、物理图像直观而被作为讨论分析的重点．然而，作为一种粗视化分析方法，半波带法存在局限性，首先，通过与积分法严格求解得到的结果对比发现，半波带法在确定明纹出现的衍射角条件时存在误差，即仅能给出明条纹出现的近似条件；其次，半波带法无法给出衍射光强表达式，即通过半波带法不能确定观察屏上任意点的光强分布；再次，半波带法不能充分体现衍射现象与干涉现象之间的区别．

赵凯华先生在其编写的面向物理专业本科生的光学教材[1]中，在菲涅耳圆孔衍射部分，对半波带法进行了补充：对于圆孔内包含非整数个半波带的情形，采用振幅矢量图解法对半波带进行了细致处理，由此求解了衍射场的振幅；在夫琅禾费单缝衍射部分，没有采用半波带法进行定性分析，直接采用振幅矢量图解法和积分法严格求解了衍射光强分布公式．在面向非物理专业的大学物理教材中，由于夫琅禾费衍射计算简单且应用广泛，一般仅讲授夫琅禾费衍射，而且把直观的半波带法作为讨论分析夫琅禾费单缝衍射的重点方法，然而并不指出半波带法存在的误差[2～5]，或者仅对这一误差做一标注，不进行说明或展开解释[6]．

本文将在半波带法的基础上对单缝波阵面进行了更精细的分割，采用振幅矢量图解法讨论明暗条纹条件，修正半波带法所给出的明纹条件公式．同时，利用该方法定量求解单缝夫琅禾费衍射光强表达式．由于该方法将单缝波阵面从有限个半波带进一步细分成无限个窄波带，这一处理充分体现了衍射现象和干涉现象之间的区别和所采取的计算方法的不同．

2 半波带法局限性分析

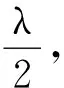
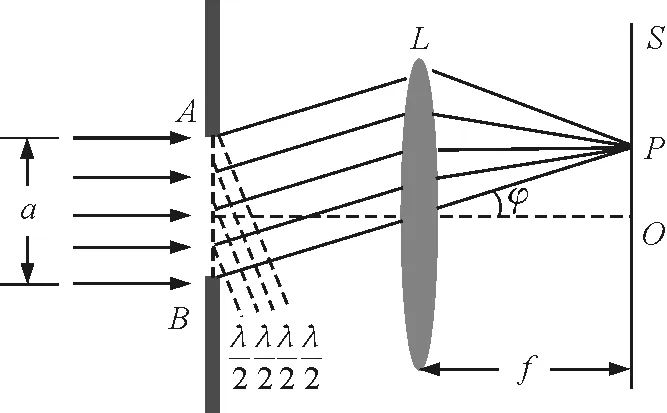
图1 半波带法分析单缝夫琅禾费衍射示意图

若单缝处的波阵面恰好被分成偶数个半波带，则P点的合振幅为零，P点处为衍射暗纹，因此暗纹出现的衍射角条件为

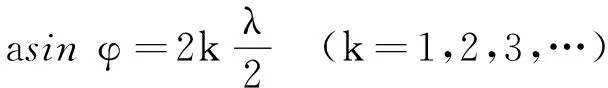
(1)

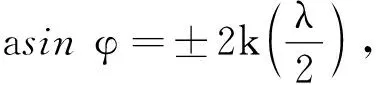
若单缝处的波阵面恰好被分成奇数个半波带，因相邻两半波带在P点的振动相互抵消，剩下的一个半波带发出的光未被抵消，会聚于P点，形成亮点，故P点处为明纹，因此明纹出现的衍射角条件为

(2)

将半波带法给出的明暗条纹条件与积分法严格求解得到明暗条纹条件对比，发现半波带法给出的暗条纹条件是精确的，而明条纹条件则不然．

下面我们将式(2)给出的明纹条件与积分法严格求解得到的明纹条件[2]分别列出，如表1所示.

表1 半波带法与积分法给出的明纹衍射角条件对比

将表1中的数据对比发现，半波带法给出的明纹条件与精确值存在偏差．具体来讲，由半波带法分析得出的明纹衍射角总是略大于积分法求得的明纹衍射角，在k值较小时差别较明显，随着k值的增大逐渐趋近精确值，这说明半波带法仅能给出明纹出现的近似条件．

3 振幅矢量图解法剖析半波带法明纹条件的近似性

由此给出了明暗条纹出现的条件

暗纹N=2k；

明纹N=2k+1,(k=1,2,3,…)．

然而由于衍射角φ是连续变化的，因此N也会随之连续变化，即N不应局限于整数．半波带法仅考虑了N是整数的情况，即仅对某些特定衍射角(使得单缝波面恰好被分成整数个半波带)做了分析，而没有针对任意衍射角作一般分析．半波带法对单缝波面的这一粗视化分割使得对明纹条件的判断不够精确，下面在半波带法的基础上对单缝波面进行更精细化的分割，并采用振幅矢量图解法来分析明暗条纹条件．

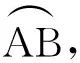
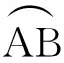
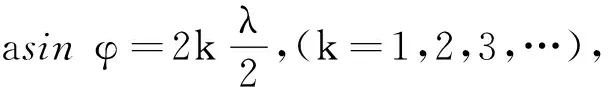
这与半波带法得到的结果一致．

图2 振幅矢量图解法分析单缝夫琅禾费衍射示意图

(3)

可见P点的振幅A为ε的函数．下面我们将上式两边对ε求导，得

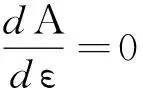
上式为超越方程，可以采用作图法来定解．下面列出部分解.

表2 超越方程的解

当ε取上述值时，P点的振幅A取极值(极大值或极小值)．根据图2(d)容易判断A的最小值发生在ε=0处，为Amin=0，因此ε取表中的数值时，P点的振幅A取极大值，P点为明纹．根据表中数据可判断，ε的取值范围为0<ε<1，且随着k值的增大，ε愈加趋向于1．由此，我们得到明纹条件为

(0<ε<1,k=1,2,3,…)(k增大，ε→1)

(4)

将表2中的ε值代入上式，并与表1中积分法给出的结果比较发现，两者非常一致，这说明上述方法由于在半波带法的基础上对单缝波阵面进行了更加精细的分割，从而克服了半波带法的局限性，精确地确定了明纹条件．

图3 单缝波面分成(2k+ε)个半波带和(2k+1)个半波带两种情况下的衍射场振幅大小定性分析

4 振幅矢量图解法求解衍射光强

由

得

将之代入式(3)，并考虑光强I=A2得

(5)

上面采用振幅矢量图解法推导出了单缝夫琅禾费衍射光强表达式，与积分法推导衍射光强表达式相比，这一方法避免了复杂的积分运算，物理思路简单，易于学生接受．

5 结论

本文首先通过对比半波带法与积分法所给出的明暗条纹出现的衍射角条件，指出了半波带法在判断明纹条件时存在方法误差．通过将粗视化的半波带法精细化，即对单缝波阵面进行更精细化分割，采用振幅矢量图解法讨论了明纹条件，修正了半波带法所给出的明纹条件公式．修正后的明纹条件表明决定单缝衍射明纹振幅的不足一个半波带，而并非恰好一个半波带．同时，利用该方法还求得了与积分法一致的衍射光强表达式．此外，由于该方法将单缝波阵面从有限个半波带进一步细分成无限个窄波带，接收屏P点的衍射光强即为从无限个窄波带发出的子波的相干叠加，因此这一方法体现出了衍射现象与干涉现象的区别，有利于学生加深对衍射现象本质的理解．

振幅矢量图解法已在大学物理的先修内容——简谐振动部分学习到，在此再次使用这一方法来分析单缝夫琅禾费衍射，有利于学生通过关联和对比加深对两部分内容的理解，也更突显了物理方法在大学物理教学中的重要性．