行星做椭圆轨道运动周期和能量的证明
张海利 侯 恕
(东北师范大学物理学院 吉林 长春 130024)
1 问题引出
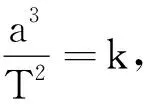
在本文的推导中需要引入角动量的知识,角动量是描述物体转动状态的物理量,角动量是参考点到质点的位置矢量与质点动量的叉乘,是矢量.角动量的方向一定垂直于位置矢量与质点的动量所构成的平面,表达式为L=r×mv,大小为L=mvτr,其中L是行星角动量的大小,vτ是垂直于径向方向的速度,r是行星到太阳之间的距离[2].
2 公式推导
行星在太阳引力作用下沿椭圆轨道运动,轨道如图1所示,行星和太阳的连线在相等的时间间隔内扫过的面积相等.

图1 行星角动量沿椭圆轨道运动
设行星的质量为m,行星到太阳之间的距离为r,其在dt时间内扫过的面积为
单位时间内扫过的面积为
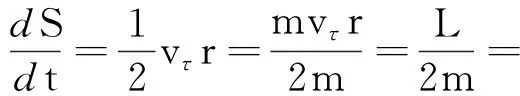
(1)
式中L为行星角动量的大小.
如图2所示,A和B分别为行星的远日点和近日点,v1和v2分别表示在远日点和近日点的速度,下面对行星做椭圆轨道运动的周期和能量做一证明.

图2 远日点和近日点及其速度
由图2中的几何关系可知
r1=a+cr2=a-c
其中r1+r2=2a
r1·r2=a2-c2=b2
(2)
行星运动总机械能E等于其动能与势能之和,设行星到太阳之间的距离为r,角动量的大小为L,近日点和远日点的机械能和角动量可表示为
(3)
L=mvr
(4)
将式(4)代入式(3)得
(5)
对式(5)变形得
(6)
r1和r2为方程(6)的解,结合式(2)并由韦达定理有[3]
(7)
(8)
由式(7)推得
(9)
由式(8)推得
(10)
由式(1)推得行星运动的周期为
(11)
式中πab为椭圆的面积.
将式(9)及式(10)代入式(11)得到
(12)
由式(12)可得
则行星做椭圆轨道运动的周期和能量为
其中M是太阳的质量,G是引力常数,a是半长轴.
行星做椭圆轨道运动周期和能量的公式在解决问题中有很大的用处,下面的典型问题就是公式的实际应用.
3 解题应用
3.1 典型问题1
要发射一颗人造地球卫星,使它在半径为r2的预定轨道上绕地球做匀速圆周运动,为此先将卫星发射到半径为r1的近地暂行轨道上绕地球做匀速圆周运动.如图3所示,在A点,实际使卫星速度增加,从而使卫星进入一个椭圆的转移轨道上,当卫星到达转移轨道的远地点B时,再次改变卫星速度,使它进入预定轨道运行,试求在椭圆轨道上A点,B点的速度和卫星从A点到达B点所需的时间,设万有引力恒量为G,地球质量为M.

图3 典型问题1题图
分析:以vA和vB分别表示卫星在椭圆轨道上A点和B点的速度,在椭圆轨道上A点和B点的机械能等于动能和势能之和,根据推导出的行星能量的公式列式,有

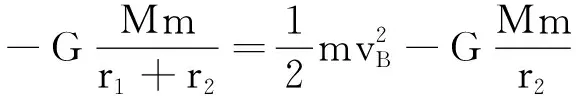
解得
卫星做椭圆轨道运动的周期
则卫星从A点运动到B点所需时间
3.2 典型问题2
从赤道上C点发射洲际导弹,使之精确地击中北极点N,要求发射所用的能量最少.假定地球是一质量均匀分布的半径为R的球体,R=6 400 km.若不考虑地球的自转,则最小发射速度的大小为多少?
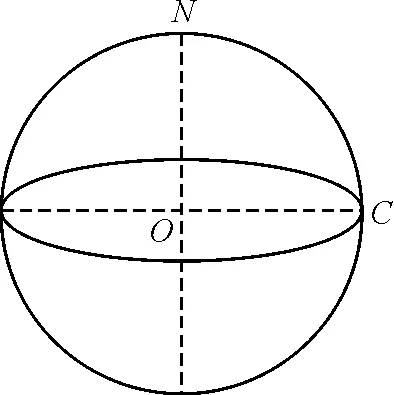
图4 典型问题2题图


图5 几何关系分析
由几何关系可知
设发射时导弹的速度为v,则有
代入数据得
v=7.2 km/s

