时变曲线交点的视觉速度和加速度
吴逸飞 胡雨晨
(武汉市黄陂第一中学 湖北 武汉 430300)
邱为钢
(湖州师范学院求真学院 浙江 湖州 313000)
在一些竞赛辅导资料中,有这样求运动曲线交点速度的题目.两个直杆,或者一个直杆一个圆环,或者两个圆环,它们在运动,求两杆交点的速度.这种做法其实是没有物理意义的,交点并不是真实的点,只是视觉意义上的交点.如果从更高维度来看,三维空间相隔一段距离平行放置的两个杆,从不同角度看,可以有交点,也可以没有交点.文献[1~3]利用速度分解合成法和相对运动法,求得了一些简单运动曲线交点视觉速度.这两种方法,对于最一般情况下随时间变化曲线交点视觉速度和加速度,很难推广.把曲线看作杆(刚体),那么曲线的变化只有刚体的转动和平动,但曲线的变化还能是形状的变化,所以我们要考虑最一般随时间变化的曲线,而不能局限于运动曲线.其次,文献只考虑匀速或者匀速转动的曲线,而没有考虑到变速运动的曲线,忽略了时变曲线交点的视觉加速度问题.最后,三维空间中3个曲面如果能交在同一点上,那么文献所用的方法是否能推广到求交点的视觉速度和加速度?我们发现,跳出文献所用的框架,另起炉灶,利用时变曲线的隐含数表达式和偏导数的知识,可以求得时变曲线交点视觉速度和加速度的解析表达式.
先考虑两维曲线,设两个时变曲线的隐函数表达式为
f(x,y,t)=0g(x,y,t)=0
(1)
式(1)理论上可以求出这两个时变曲线依赖于时间的交点坐标x=x(t),y=y(t),由这个形式解,定义交点的视觉速度和加速度为
(2)
但是一般情况下,这个交点坐标的显式解析表达式很难得到.给定参数,交点的数值解是可以求得的.先定义以下矩阵,其具体含义在下文的推导中可以看出
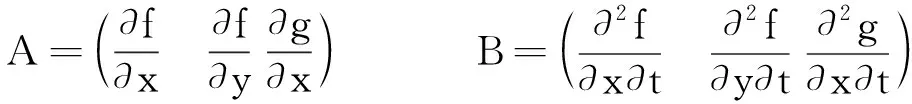
(3)
定义形式上的曲线速度
加速度为
对式(1)中两个等式两边做全微分,得到
(4)
式(4)中两个等式两边除以dt,再移项,得到
(5)
式(3)可以写成Av=-vcur
(6)
于是两个时变曲线交点的视觉速度有形式意义上的解
v=-A-1vcur
(7)
式(5)继续对时间t求偏导,得到

(8)
(9)
定义一个矢量C=(vTFv,vTGv), 那么(8)、(9)两式可以写成矩阵形式
t=0
Aa=-acur-2Bv-C
(10)
于是两个时变曲线交点的视觉加速度有形式意义上的解
a=-A-1acur-2A-1Bv-A-1C
(11)
式(7)和式(11)就是两个时变曲线交点的视觉速度和加速度的一般表达式.
以上处理方法的一个好处是很容易能推广到3个时变曲面交点的视觉速度和加速度计算,不需要画图.我们以一个具体的例子来说明如何计算. 设有两个时变平面和一个时变球面, 它们的方程是
(12)
上式两边对时间求导,得到
(13)
在时间t=0时3个面的交点坐标是(1,1,1),代入式(13),解得交点的视觉速度为
(14)
式(13)继续对时间求导,得到
(15)
代入t=0时交点的坐标和视觉速度,计算得到此时交点的视觉加速度为
(16)
现在数学符号计算软件非常发达,很容易编程计算以上表达式.有兴趣的读者不妨利用本文的方法和结论来出一些相关的物理竞赛模拟题.

