基于小波能量系数和神经网络的管道缺陷识别

姜银方，郭华杰，陈志伟，2，杜 斌，2，刘秋阁，2

(1.江苏大学 机械工程学院，江苏 镇江 212013;2.江苏省特种设备安全监督检验研究院 镇江分院，江苏 镇江 212009)

管道事故危害人们的生命财产，也造成了一定程度的生态破坏，对管道进行有效地检测是避免管道事故的有效手段。

超声导波检测方法在管道无损检测方面具有无须大面积开挖管道或剥离管道防腐层、检测距离远、效率高等优势，但由于回波波形复杂，难以直接从信号中分辨出是管道缺陷还是管道结构，只有经过专门的培训才能给出比较准确的判别，这就需要一种可靠的智能化判别方法。刘振清［1］等介绍了人工神经网络在超声检测中的应用;赵彩萍［2］、吴斌［3］、杨帆［4］等将神经网络应用于对管道缺陷的识别研究;孙炳章［5］和符浩［6］分别从检测信号的小波奇异点和相关程度的角度出发进行了研究。众多学者从不同的角度进行了研究并取得了一定的成果，但识别缺陷的准确性还有较大的提升空间。

本将构建了试验系统，采集焊缝和凹槽缺陷的检测数据，编写Matlab 程序，截取焊缝和凹槽处的检测信号并提取出小波能量系数，结合BP 神经网络对焊缝和凹槽进行分类识别研究。

1 超声导波的特性

多模态和频散是管道导波的两个基本特性。管道导波包括纵向轴对称模态、扭转轴对称模态及非轴对称弯曲模态，Silk 和Bainton 将这3 种模态分别记为L(0，n)，T(0，n)及F(n，m)，n 表示模态导波绕管壁传播的周向阶数，m 表示模态导波纵向振动阶数［7］。利用英国帝国理工大学开发的Dispers［8］软件绘制出外径108 mm，壁厚5 mm 的碳钢管群速度频散曲线如图1所示，同一检测频率下存在多个模态，导波波速会随着频率的改变而产生一定的变化。本文使用L(0，2)模态的超声导波进行试验，其传播速度快，对管道内壁和外壁的缺陷有相同检测性能。

图1 碳钢管(外径108 mm，壁厚5 mm)的群速度频散曲线

导波在传播过程遇到管道焊缝、缺陷等不连续或不均匀的位置，会产生明显的反射回波，而反射回波信号中含有位置、程度等信息，但由于波形复杂，通常需要借助适当的分析方法提取出隐藏的有用信息，才能准确评估管道状况。

此外，导波传播过程中会有衰减，随着导波自身频率的增加，能量衰减会加剧，有效传播距离将变短;低频有效传播较远而检测精度较低，高频检测的精度较高但传播距离较近，这就要求在管道检测时要选择合适的检测频率。

2 小波能量系数

若被检管道上存在管道结构或缺陷，在相对应的位置发生能量聚焦形成反射回波，而能量通常聚集在某一段频率上，能量聚集的情况与管道缺陷的情况存在一定的联系。

小波分解可将信号分解为低频段和高频段，而导波能量随之被分解到不同频带，通过多层小波分解方式能够将信号分解到不同频率成分的多个子空间中，各个子空间占有总能量的比重存在差异。如图2 所示，利用多层小波分解方法将一个完整的导波检测信号进行3 层分解得到4 组信号，分别计算各组信号的能量值得到各组信号的能量分布;从图2 中可发现:不同组的信号对应的能量值差异较大，第2 和第3 组信号与原始信号外形轮廓最为相似，所占用的能量成分也较高，分别为4.59%和93.26%。以上现象表明小波子空间能量系数在某种程度上能表征检测信号的能量分布特征。

3 试验结果及分析

3.1 管道试验

试验系统包括波形函数发生器AFG3011C、数字示波器LDS31010、前置放大器PAI、前置供电信号分离器、压电传感器阵列、管道及计算机，试验情况如图3所示;本文的试验对象为带焊缝和凹槽缺陷的规格均为108 mm×5 mm 的多根碳钢管道，图4 为一组管道焊缝和凹槽的照片。

图2 3 层小波分解及各层能量系数

图3 碳钢管(外径108 mm，壁厚5 mm)的实验系统示意图

图4 碳钢管焊缝及凹槽实物图

在管道一端环形均匀布置两环规格为25 mm×4 mm×1 mm 的PZT－5 压电陶瓷片，每环16 片，一环用作激励，另一环用作接收。在试验过程中发现激励频率在90 ～105 kHz 范围时回波信号幅值比较清晰明显，采集该频率段的信号进行研究，图5 为一组激励频率为90 kHz 时管道焊缝和凹槽的检测信号。

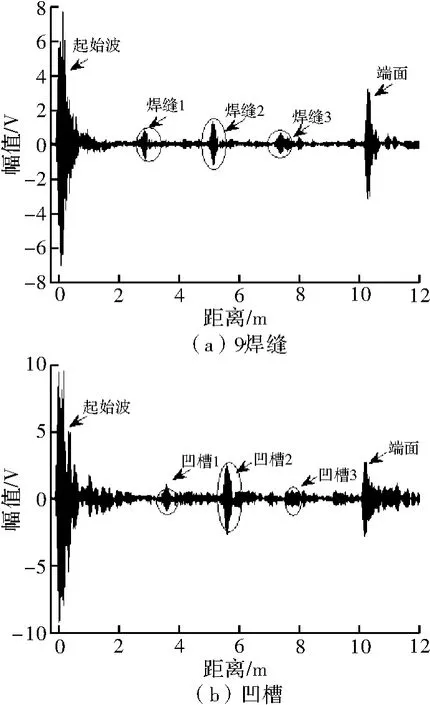
图5 90 kHz 时管道焊缝和凹槽的检测信号

3.2 试验结果及分析

本文利用小波能量系数结合BP 神经网络对管道缺陷进行分类识别的研究。选取小波能量值作为一组特征向量，为避免向量过大带来的数据冗余和向量太小导致的信息特征不足，对采集数据进行了试验分析，通过分析发现:小波分解层数为6 层时对各类检测信号划分效果较好。使用小波6 层分解方法提取小波能量系数，即小波子空间信号能量占检测信号能量的百分比，该参数为无量纲参数，其提取流程如图6 所示。本文使用的Matlab 程序代码为“［c，l］=wavedec(x，6，‘db9’);［Ea，Ed］=wenergy(c，l);”，在该代码中db9为小波基函数，wavedec 和waverec 为Matlab 小波工具箱中自带的函数，Ea和Ed为小波能量系数，x 为截取的时域数据，x 的长度为激励波波长的1.5 倍

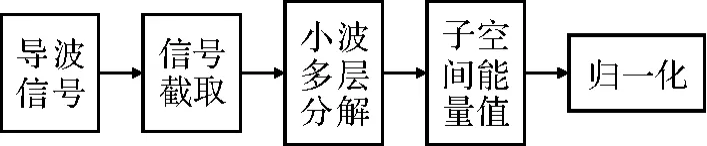
图6 小波能量特征提取流程图

表1 BP 神经网络参数

构建如表1 所示BP 神经网络模型，选用的传递函数依次为tansig、logsig 和purelin，训练函数为raingdm;训练时使用［1 0］和［0 1］作为标准输出结果，分别表示焊缝和凹槽;通过比较训练结果与标准输出结果的标准差判别所属类别，例如，输出结果为［0.9 0.6］，与［1 0］和［0 1］的标准差分别为0.495 和0.919 2，表明输出结果与焊缝的标准输出结果最为接近，则判定结果为焊缝。

焊缝和凹槽的总样本数分别为60 和660 个，试验中使用等概率筛选的方式选取训练和识别样本。表5为5 次独立试验的情况，从表中可以看出:识别准确率最高为1，最低为0.92;凹槽的样本多，其识别准确性稳定，5 次独立试验的缺

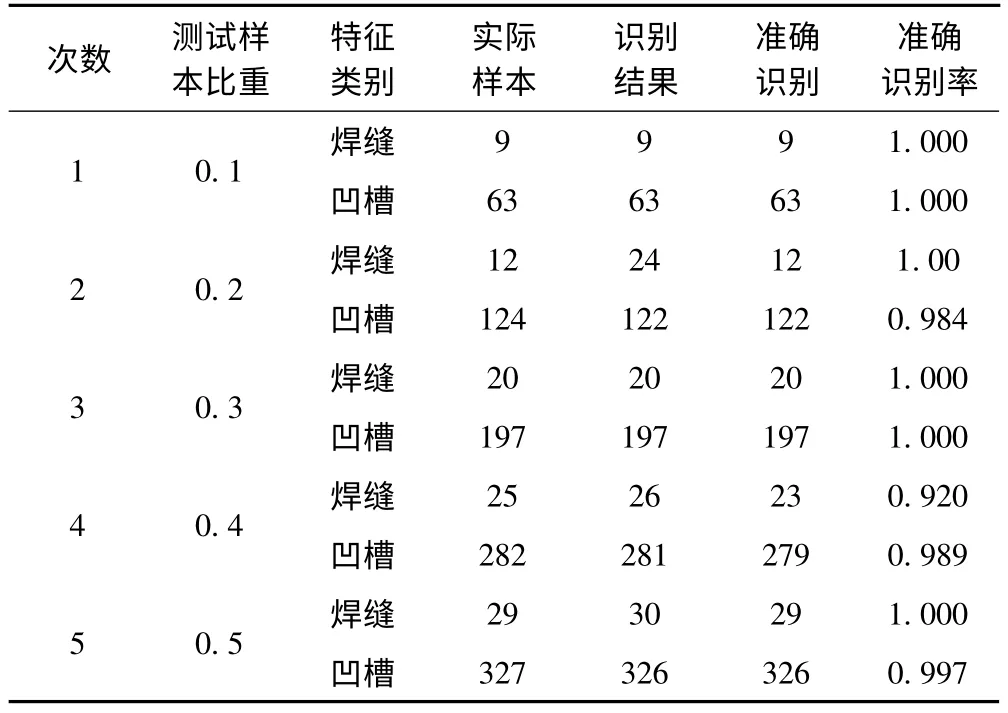
表2 BP 神经网络训练与判别结

图7 第1 次试验的BP 神经网络的收敛曲线

陷识别准确率均高于0.98，甚至识别完全正确;焊缝的样本少，识别准确性波动较大，但均不低于0.92。以上现象表明该方法具有较高的识别准确率，且样本量越多，其识别性能越稳定。图7 为第1 次试验的收敛曲线在迭代次数达到1 498 时收敛误差接近0.001，表明该方法训练过程的收敛性能良好。

4 结束语

本文使用小波方法对检测信号进行6 层分解，提取出小波能量系数并应用于BP 神经网络的识别管道缺陷的研究;多次随机试验的研究结果表明，该方法的对凹槽缺陷的识别准确率均高于0.98，且样本个数越多，识别准确率越稳定，表明该方法在缺陷识别方面的准确率较高且稳定可靠。

［1］ 刘镇清，张海燕.人工神经网络及其在超声检测中的应用［J］.无损检测，2001(5):221－225.

［2］ 赵彩萍，王维斌，何存富，等.基于神经网络的超声导波管道缺陷识别［J］.传感器与微系统，2009(11):19－21，24.

［3］ 吴斌，齐文博，何存富，等.基于神经网络的超声导波钢杆缺陷识别［J］.工程力学，2013(2):470－476.

［4］ 杨帆.管道超声导波检测信号分析处理与识别研究［D］.成都:西南石油大学，2012.

［5］ 孙炳章.小波分析和神经网络在超声检测系统中的应用［D］.青岛:山东科技大学，2004.

［6］ 符浩，王维斌，周进节，等.基于相关的超声导波检测信号分析方法［J］.压力容器，2011(7):59－64.

［7］ Silk M G，Bainton K F.The propagation in metal tubing of ultrasonic wave modes equivalent to Lamb waves［J］.Ultrasonics，1979，17(1):11－19.

［8］ Pavlakovic B，Lowe M，Alleyne D，et al.Disperse:a general purpose program for creating dispersion curves［M］.Berlin:Springer，1997.