斜视SAR 原始回波数据频域模拟快速算法

王锦章

(海军驻北京地区电子设备军事代表室，北京 100070)

斜视合成孔径雷达不但具有传统正侧视合成孔径雷达全天时、全天候、远距离获得高分辨图像的特点，并具有较高的灵活性和机动性，能通过控制波束指向对感兴趣的目标区域进行成像，对军事上实现侦查和打击具有重要战略意义。近年来，已成为SAR 研究的热点课题。

合成孔径雷达原始数据模拟技术在SAR 系统设计和算法研究等领域都具有重要的作用。SAR 回波仿真算法基本上可分为二维频域算法［1－4］和时域算法［5］，基于回波数学模型的时域算法能够精确地模拟出SAR 原始回波信号，物理概念清晰，但计算复杂度过高，不适于大场景目标;二维频域算法直接推导了系统传递函数的二维频域表达式，利用频域内的FFT 代替了时域卷积，大幅提高了仿真速度。传统二维频域算法的推导主要基于正侧视模式SAR，当处于斜视工作模式下时，距离向和方位向存在严重的耦合，传统二维频域算法无法准确模拟出距离徙动的空变特性［6－7］，Franceschetti 等人虽根据斜视SAR 的几何构型重新推导了系统传递函数，但在斜视情况误差明显增大，文献［2］对斜视原始数据快速算法进行了研究，提出了沿距离向积分的快速算法，虽保证了模拟精度，但其效率远不如二维频域算法。去走动处理在斜视成像算法中经常使用，以避免频谱混叠等问题。斜视情况下，回波距离方位耦合严重，在回波模拟算法中，可先推导出去走动后的系统传递函数，再在算法最后统一模拟距离走动，完成回波模拟，这样可避免斜视带来的频谱混叠、高脉冲重频等问题，从而提高回波数据的准确度［8］。

本文提出一种斜视模式下的原始回波数据二维频域快速算法，算法通过去走动处理将多普勒中心搬移到零多普勒处，重新推导了去走动后的系统传递函数，在距离频域－方位时域上模拟了距离走动，并模拟出了回波的空变特性，保证了回波数据的准确性，性能分析表明，本算法的计算效率远高于时域算法以及沿距离向积分算法。

1 斜视SAR 系统传递函数

超宽带SAR 的几何模型如图1 所示，载机沿y 轴飞行，飞行高度为h，速度为v，P 点为场景中心点目标，斜视角为θ，tm=0 时刻，载机位于B 点。

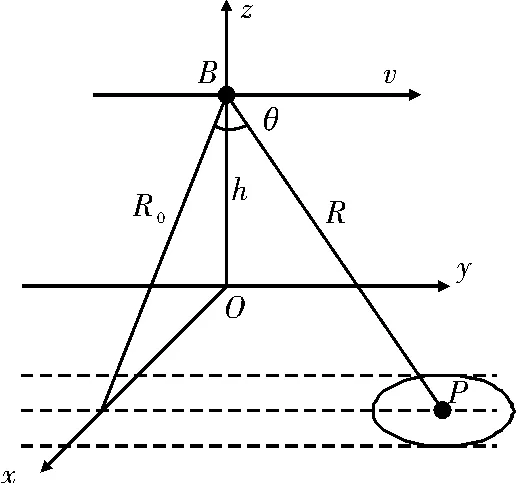
图1 超宽带SAR 的几何模型

由图1 可知，任意时刻tm，系统的瞬时斜距变化方程为

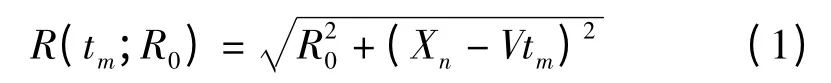
在tm=0 时刻，将斜距变化方程进行泰勒级数展开

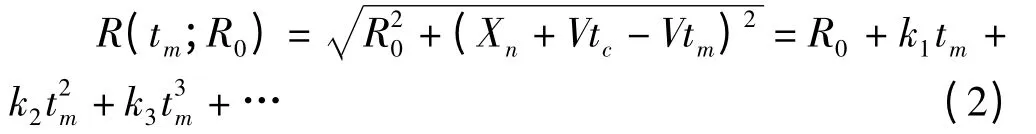
其中，k1=－sinθ·V，k2=cos2θ·V2/R0。

假设雷达发射线性调频信号，则雷达接收的回波基带信号可写为

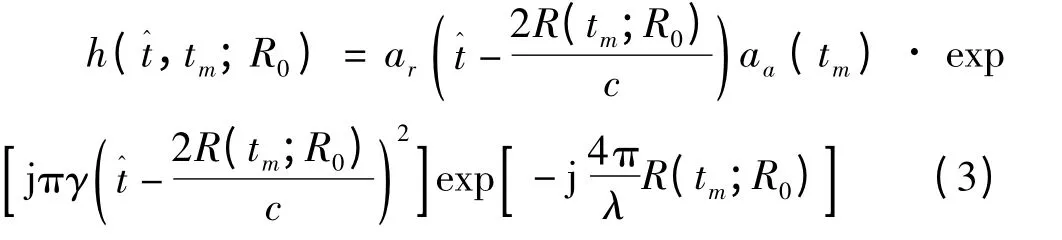
对式(3)中快时间做傅里叶变换后得到

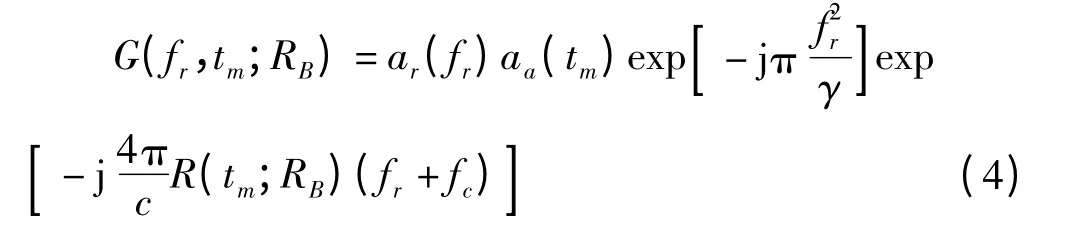
这里线性走动项为

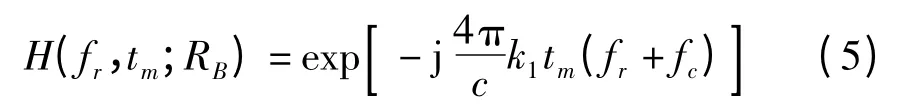
所以，式(4)可写为线性走动项与其他徙动项加和的形式

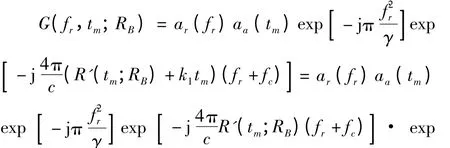
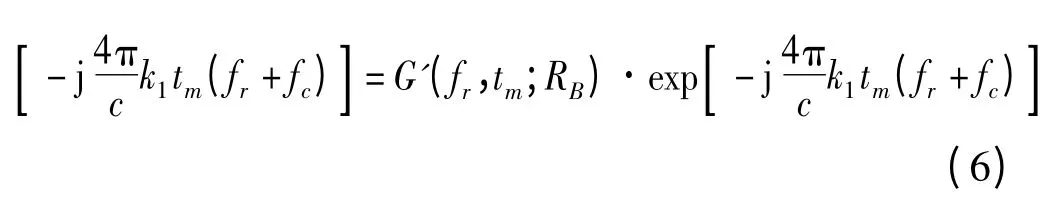
其中

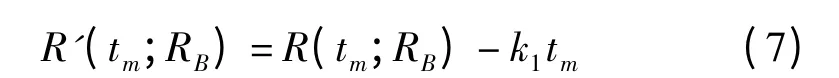
首先将去走动后的传递函数G'(fr，tm;RB)进行模拟，最后再统一对线性走动项进行模拟，去走动后斜视传递函数变为

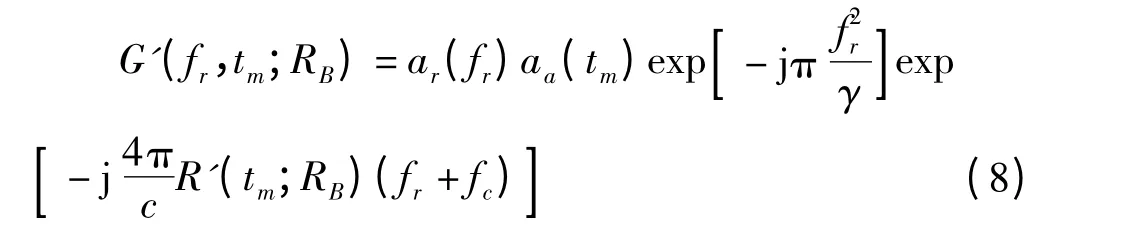
则根据驻相点原理，对系统传递函数(8)慢时间做傅里叶变换得到去斜后的传递函数二维频域表达式为

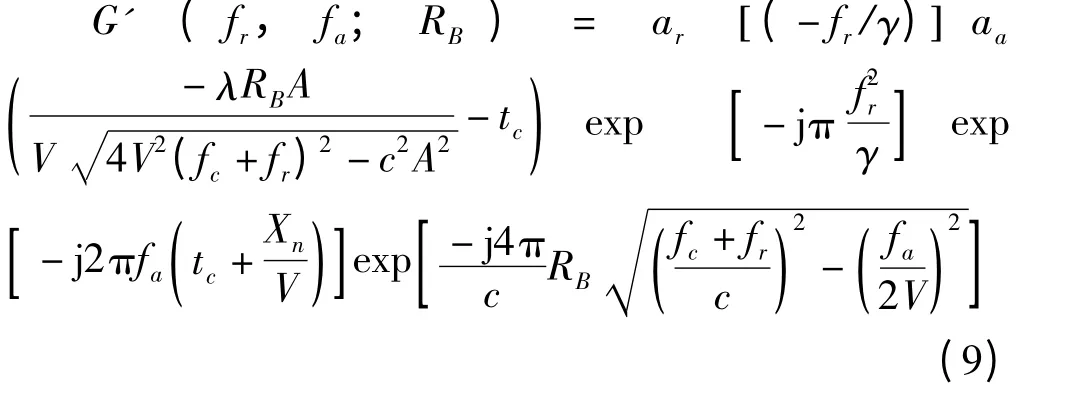
2 斜视SAR 原始数据二维频域模拟算法

假设场景的二维复散射系数为γ(y，r)，y 为目标在方位上偏移场景中心的距离，r 为目标在距离上偏离场景中心的距离，则场景的回波信号为

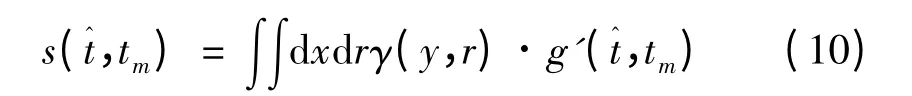
对场景的回波信号做二维傅里叶变换，其二维频域的表达式为

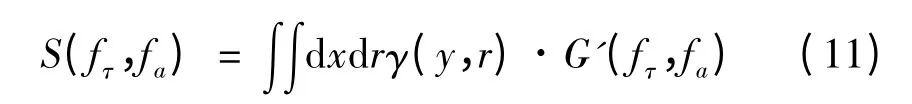
将式(9)带入式(11)可得

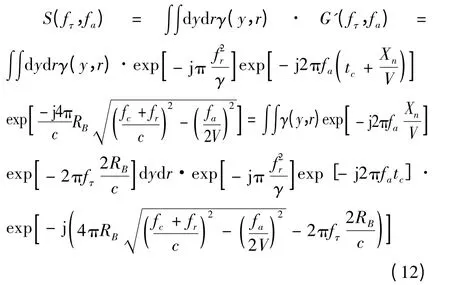
其中，Ff，ftm［·］表示方位距离二维FFT;G0(f，ftm)为传递函数

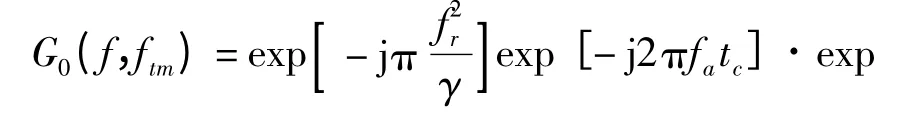
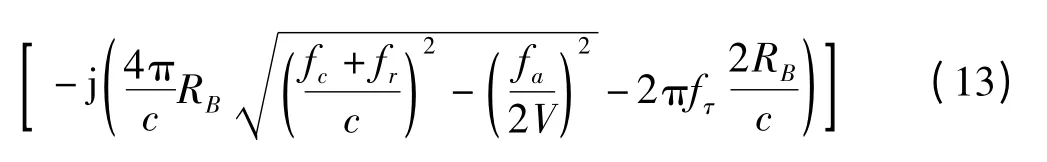
在距离频域－方位时域上模拟距离走动，生成回波。在距离频域－方位时域，系统传递函数的表达式为

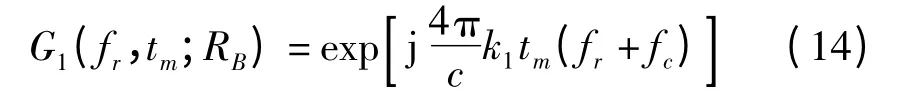
由传递函数可知，在距离频域－方位时域上乘以一次项G1(fr，tm;RB)即可模拟出斜视SAR 回波的距离走动，图2 给出了算法的示意图。

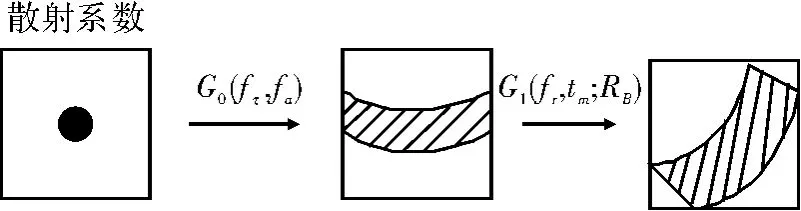
图2 斜视SAR 回波生成示意图

若没有距离走动或不校正距离走动，距离压缩后相同距离单元里点目标的斜距是相同的，当时域校正距离走动后，同一距离单元的点目标在tm时刻的斜距为R0+ΔR(tm)，从而使多普勒调频率不再是一个常数

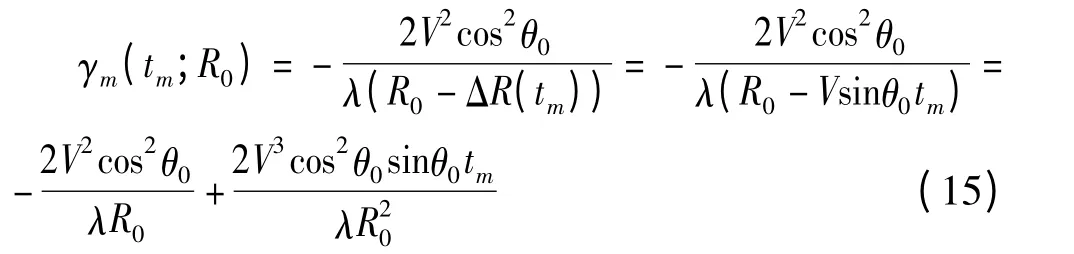
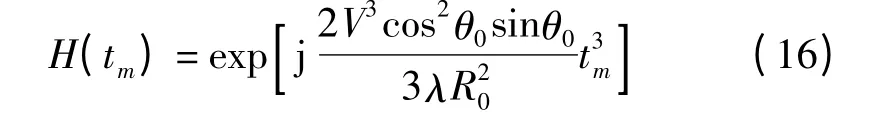
同样，利用此函数对空变性进行模拟，从而得到准确的回波数据。

由以上论述可知，斜视SAR 二维频域回波模拟算法的流程图如图3 所示。

Frank H.Hong［12］等人给出了补偿空变性的函数

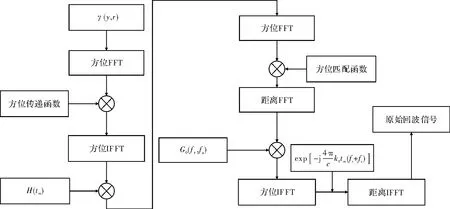
图3 算法流程图

这里，方位传递函数为

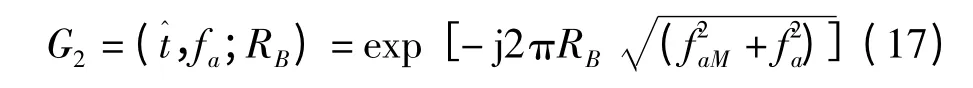
3 仿真实验

为了验证本算法的高效性和正确性，进行了计算机仿真，仿真参数如表1 所示。

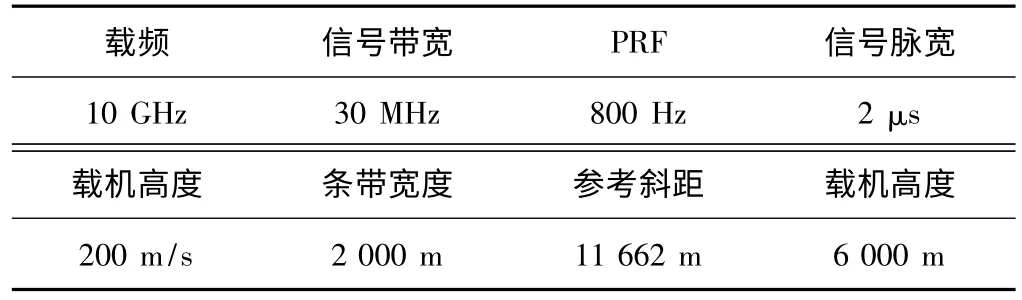
表1 SAR 参数

斜视角设置为60°，分别用时域方法以及本文所述的二维频域方法进行仿真。为验证斜视SAR 原始数据频域模拟方法对于大场景目标的模拟性能，设置两个点目标，目标1 设置于场景中心，目标2 设置于距场景中心500 m 处。

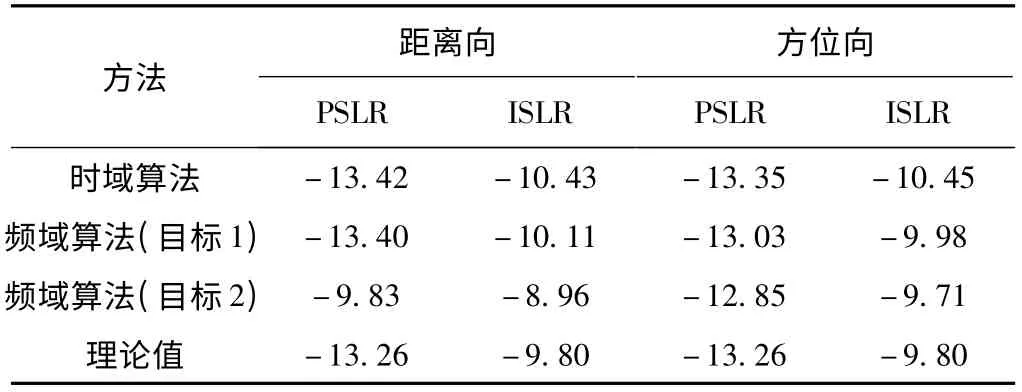
表2 点目标成像结果性能分析

图4 为点目标在方位向和距离向的脉冲响应结果。可以看出，在斜视角为60°的情况下，目标1 与目标2 均可得到良好的聚焦。表2 给出了成像性能指标，可以看出，目标1 与目标2 在距离向和方位向的峰值旁瓣比(PSLR)以及积分旁瓣比与时域模拟方法的相应数值都比较接近。图5 给出了本文所述回波产生方法与理论值相比的相位误差，在孔径范围内，场景中心点目标最大距离相位误差为0.3 rad，最大方位相位误差为0.2 rad，距离场景500 处的点目标最大距离相位误差为0.35 rad，最大方位相位误差为0.4 rad，均远＜π/4 rad，其影响可忽略。仿真结果表明本算法能仿真出较为准确的回波信号。

图4 点目标成像结果

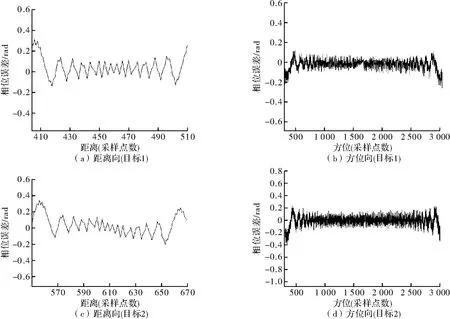
图5 相位误差

4 结束语

本文提出了一种高效的斜视SAR 回波原始数据模拟算法。文章从斜视SAR 的几何构型出发，重新推导了去走动情况下系统传递函数，并在距离频域－方位时域上模拟了距离走动，在距离－方位时域模拟了回波的空变特性，保证了回波数据的准确性，仿真结果证明了本算法的正确性以及高效性。

［1］ Franceschetti G，Iodice A，Perna S，et al.Efficient simulation of airborne SAR raw data of extended scenes［J］.IEEE Transactions on Geoscience and Remote Sensing，2006，44(10):2851－2860.

［2］ 刁桂杰，许小剑.大斜视SAR 原始数据的快速模拟算法研究［J］.电子信息学报，2011，33(3):684－689.

［3］ Francesschetti G，Iodice A，Perna S，et al.SAR sensor trajectory deviations:fourier domain formulation and extended scene simulation of raw signal［J］.IEEE Transactions on Geoscience and Remote Sensing，2006，44(9):2323－2334.

［4］ 马兵强，于彬彬，刘畅，等.条带FMCW－SAR 回波数据的二维频域模拟算法［J］.电子与信息学报，2011，33(2):375－380.

［5］ Franceschetti G，Migliaccio M，Riccio D，et al.SARAS:A SAR raw signal simulator［J］.IEEE Transactions on Geoscience and Remote Sensing，1992，30(1):110－123.

［6］ 韦立登，李绍恩，吴一戎，等.SAR 原始回波信号生成算法的性能比较研究［J］.电子与信息学报，2005，27(2):262－265.

［7］ 汪丙南，张帆，向茂生.基于混合域的SAR 回波快速算法［J］.电子与信息学报，2011，33(3):690－695.

［8］ Mori A，Vita F D.A time－domain raw signal simulator for interferometric SAR［J］.IEEE Transactions on Geoscience and Remote Sensing，2004，42(9):1811－1817.