基于改进遗传算法的PID 参数研究
郑 权,忻尚芝,钱建秋
(上海理工大学 光电信息与计算机工程学院,上海 200093)
PID 控制因其控制系统结构简单,适用对象广泛,控制性能优异,以及近年来控制硬件的高速发展,使得PID 控制已成为工业控制中常见的一种控制方法[1],特别是在拥有精准数学模型的控制系统中。PID 控制参数的物理意义清楚[2];PID 控制器在线调整方便[3],但也存在限制着其控制精度,无法对具有不确定数学模型系统的参数进行整定和优化的问题[4]。
目前有多种PID 优化方法,如间接寻优方法、梯度法、Ziegler-Nichols 法、爬山法等。但这些方法都有自己的缺点,尤其是依赖初始值的取样,当取样无法涵盖全部控制系统信息时,这些寻优方法容易寻找局部最优解,造成寻优失败[5]。同时在实际应用中系统大多具有非线性,时变不确定性,应用常规方法难以建立准确数学模型。因此,在具有自适应参数整定与优化能力又要求算法简单的PID 控制技术,成为研究的主要方向[6]。遗传算法是一种新型的智能算法,本质是一种高效、并行、全局搜索的方法[7]。鉴于遗传算法结构的开放性,算法简单,与问题结合密切,成功地应用于求解多目标多模型的复杂问题,本文智能算法采用改进遗传算法(IGA),对PID 参数进行算法的改进,通过寻优路径的优化使参数快速的整定,明显提高了传统PID 控制器的控制精度和效果。
1 改进遗传算法
1.1 编码及初始群体生成
编码是应用遗传算法时要解决的一个关键步骤,目前常采用的编码方法主要是二进制编码方法、符号编码方法和浮点数编码方法,而基本遗传算法(SGA)使用的二进制编码不便于反应所求问题的结构特征,并且每个个体长度过大,占用计算机内存空间太多,对于一些连续函数的优化问题,也由于运算的随机特征使得局部搜索能力较差,难以提高寻优精度。为改进这个特征,本文采用格雷码(Gary Code)来进行个体编码[8],格雷码是使两个整数所对应的编码之间仅有一个码位不同,其余码位均相同。本系统中有3 个参数需要优化即为Kp,KI,Kd,可将这3 个参数组合为一个3维向量作为遗传算法中的每个独立的个体
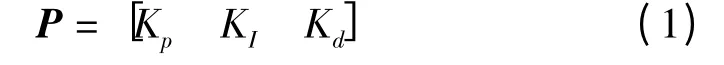
1.2 适应度函数
适应度函数也称为评价函数,是算法演化过程的驱动力,也是进行自然选择的唯一选择。本文的目标函数如式(2)所示。
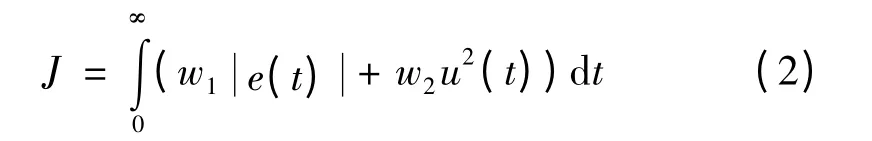
式中,e(t)为系统误差;U(t)为控制器输出;W1和W2为权值。
适应度函数值总是非负的,任何情况下都希望其值越大越好,所以将目标函数J 转换为适应度函数F,适应度值函数F 如式(3)所示。

式中,是Fmax当前生育带中目标函数的最大值。
1.3 选择
本文采用均匀排序的方法进行选择,计算种群中所有个体的适应度值,根据每个个体的适应度值占总体适应度值的比例,这个比例为其选择概率。概率计算值如式(4)所示。

其中,Fci为某一代种群中第i 个个体的适应度的值;F∑为全体适应度值的总和。
这种方法成功地避免了轮盘赌法使适应度高的个体淘汰,以及随机竞争选择法中个体选择概率相同的问题。
1.4 交叉
本文采用均匀交叉。首先系统随机生成一个与单个个体编码串长度相等的由0 和1 组成的字符串W=w1,w2,…,wl,其中L 为个体编码串长度。选出相互配对的两个个体A,B 作为父代,产生两个新一代A*,B*。当Wi=0 时,子代A*在第i 位基因继承父代A 对应的基因,子代B*在第i 位基因继承父代B 对应的基因。当Wi=1 时,子代A*在第i 位基因继承父代B 对应的基因,子代B*在第i 位基因上继承父代A 对应的基因[9]。
1.5 变异
本文采用均匀变异的方法,让群体中每个个体的基因都能拥有变异的机会。根据种群个体适应度值由小到大排序,根据式(5)计算每个个体的变异概率
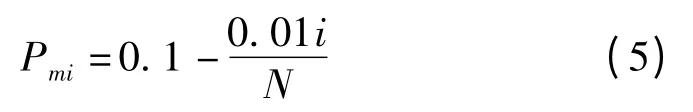
式中,Pmi为某一代种群中第i 个个体的变异率,i=1,2,3,…,N。这样就使原本适应度小的个体获得了较大的变异机会,从而使其有较高的机会变成适应度高的个体而保存下来,这样使系统的基因多样性有了保证,因为本文中有3 个变量,不会因为总体适应度不高,使一个参数的优秀基因被舍弃掉[10]。
1.6 遗传操作终止条件
传统的遗传算法是提前设定一个最大迭代次数,当到达后迭代次数时终止遗传算法的操作。但由于遗传算法是随机搜索全局最优解,寻优路径具有随机性,当运算次数达到迭代次数时,计算出来的解不一定是问题的最优解,也有在达到迭代次数前很久就已经计算出全局最优解,但一定要等到迭代次数时才能终止,这影响了控制系统的整定与优化速度。因此引入一种判断标准,当判定运算已经在某一点附近来回震荡,这时可以停止操作。这种方法计算量大,但能确保能找到全局最优解[11],本文中目标函数最小值Jmin作为这一判断的标准,当最小值小于一个阈值时终止运算。同时为了防止运算进入死循环,设定一个较大数值作为迭代次数来终止运算。以下为遗传算法流程图,如图1 所示。
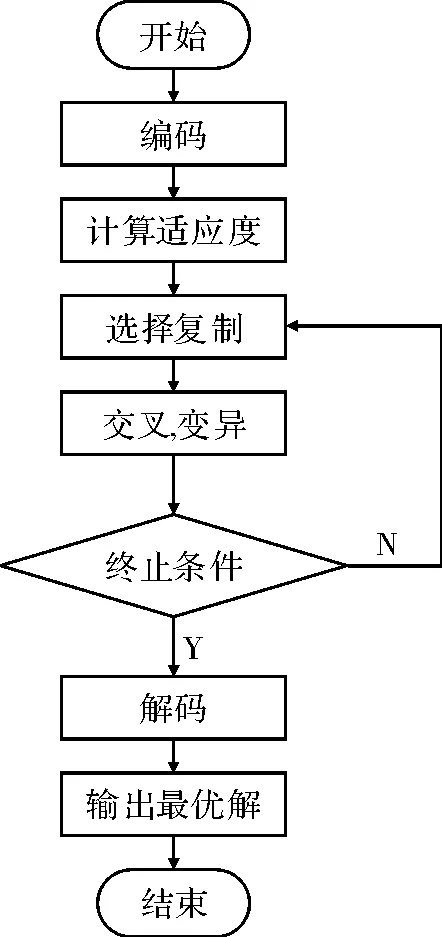
图1 遗传算法流程图
2 PID 控制器
2.1 常规PID 控制原理
PID 是比例、积分、微分3 种控制方式综合应用的控制器,简称PID 控制器。控制器适用于被控对象负荷变化较大,干扰强,要求控制质量较高的场合。其原理框图如图2 所示。

图2 PID 控制系统原理框图
PID 控制器的规律为
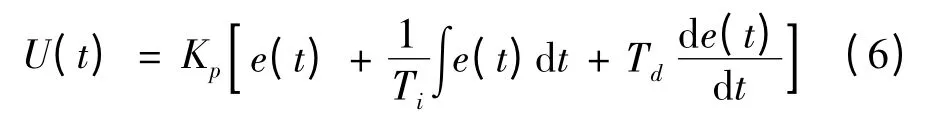
或写成传递函数的形式
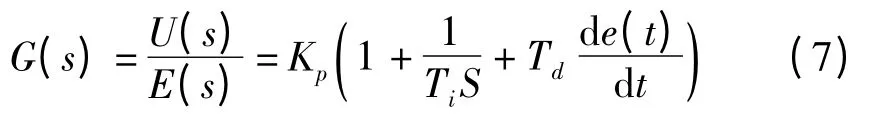
其中,Ti为采样周期;KI=Kp/Ti为积分数;Kd=Kp×Td为比例参数;Kp,KI,Kd为控制器的3 个控制参数,即为本文中待寻优的3 个参数。
2.2 基于遗传算法的PID 控制器设计
基于改进遗传算法的PID 控制器设计由传统PID控制器和遗传算法模块两部分组成。PID 控制器对被控对象进行闭环循环控制,遗传算法模块根据实际系统运行参数,进行计算,不断优化3 个参数的数值,实时调节PID 控制器的3 个参数,快速计算出最优解,从而使系统达到控制稳态的最佳效果。遗传算法模块中将PID 的Kp,KI,Kd3 个参数组合在一起作为遗传算法中的每个独立的个体。根据遗传算法流程进行编码,计算适应度,对种群进行选择、交叉、变异操作,当种群不断迭代繁殖,直到找到全局最优解。控制器系统结构如图3 所示。
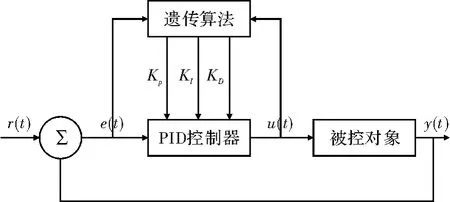
图3 基于改进遗传算法的PID 控制器设计
3 仿真
本文将用Matlab 中的Simulink 进行电阻加热炉控制系统仿真,来验证基于改进遗传算法的PID 控制器的可行性与有效性,被控对象为电阻加热器。实验模型中传递函数为

遗传算法种群数量为N=30,迭代次数为200,交叉概率Pc为0.9,变异概率Pm由式(5)得出,仿真结果如图4 所示。
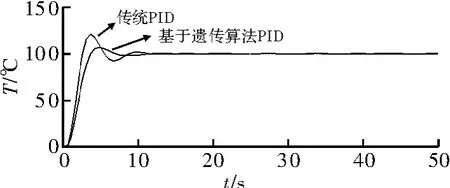
图4 仿真结果
如图4 仿真结果中的两条曲线所示,传统PID 控制,超调量有20%,调节时间为13 s。采用改进遗传算法对PID 控制器参数进行优化,超调量只有5%,调节时间为7 s,震荡时间只有传统的1/2。因此采用遗传算法,其整定速度快、优化效果好、控制系统调节时间短、震荡幅度小、超调量小,因此具有基于改进遗传算法的PID 控制器比常规PID 控制器的控制效果更优越。
图5 为Kp,KI,Kd这3 个参数的优化曲线。从图中可以看出,约在5 s 控制系统计算出了Kp,KI,Kd的3 个控制量的值,系统在5 s 时趋于稳定,并在调节时间为7 s 时达到稳态,遗传算法的优越性使系统参数的计算快速完成,减少了控制系统的调节时间,具有更好的控制效果。
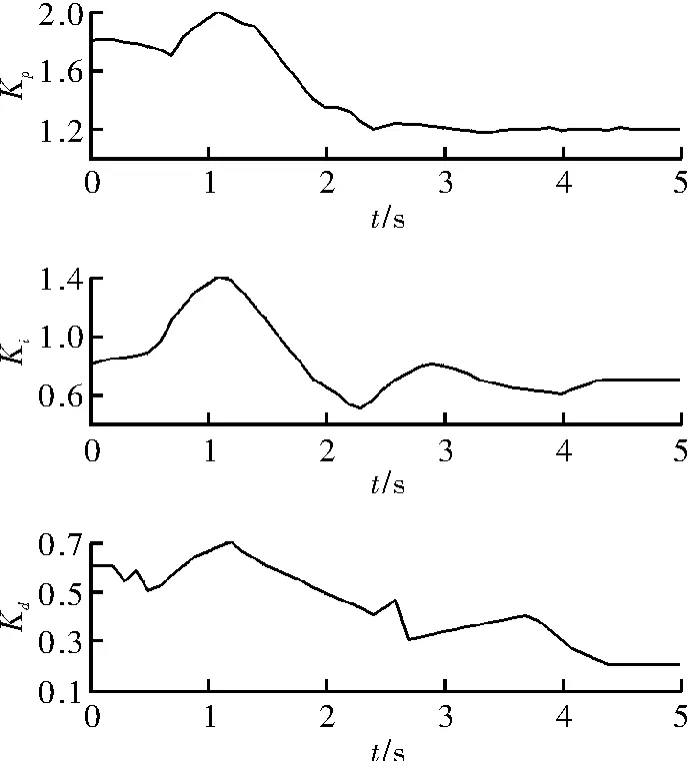
图5 3 个参数的优化曲线
4 结束语
在PID 控制器的应用设计中,PID 参数的设定是重要的一个环节。本文应用改进遗传算法设计并完成了PID 参数的整定与优化,并用Matlab 进行电阻加热器控制系统仿真,实验结果表明:基于改进遗传算法的PID 控制器要比传统PID 控制器在整定速度、优化效果、控制系统调节时间、震荡幅度、超调量等性能良好,实验也直接证明了采用改进遗传算法对PID 控制器参数进行整定和优化是有效的,并获得了更好的控制效果。
[1] 何福忠,孙优贤.基于稳定参数空间的PID 调节器遗传优化设计[J].控制与决策,2000,15(4):507-509.
[2] 郭一楠,巩敦卫.双层进化交互式遗传算法的知识提取与利用[J].控制与决策,2007,22(12):1329-1334.
[3] 张志刚,杜永贵.基于遗传算法的PID 参数整定[J].太原理工大学学报,2005,36(4):417-420.
[4] Tan Wen,Liu Jizhen.Tuning of PID controllers for boiler turbine units[J].ISA Transactions,2004,43(2):571-573.
[5] 牛芗洁,王玉洁.基于遗传算法的PID 控制器参数优化研究[J].计算机仿真,2010,27(11):180-184.
[6] 刘瑞国,邵诚.一种可自适应调节参数的改进遗传算法[J].信息与控制,2003,32(6):556-560.
[7] Vision A.Fuzzy logic based set-point weight tuning of PID controller[J].IEEE,2003,8(3):1540-1545.
[8] 陈祥光.遗传算法在PID 控制器参数寻优中的应用研究[J].计算机仿真,2001,18(2):30-32.
[9] Stella Morris,Dash P K,Basu K P.UPFC controller design for power system stabilization with improved genetic algorithm[J].IEEE,Transactions on Computer Science,2003,8(3):1540-1545.
[10]Tang K S,Man K F.Genetic algorithmic and their applications[J].IEEE Signal Process,1999,13(6):22-27.
[11]林洪涛,王敏.基于遗传算法的PID 参数整定[J].沈阳工业学院学报,2004,23(4):27-31.
——基于人力资本传递机制
——基于子女数量基本确定的情形

