基于改进的引力搜索算法的T－S 模型辨识

董新燕，丁学明，王 健

(上海理工大学 光电信息与计算机工程学院，上海 200093)

自然世界中的系统基本上是非线性的，而辨识系统［1］是建立这些复杂的非线性系统模型最有效的方法。其中T－S 模型［2－4］是一种有效的辨识工具，其采用线性方程去表示每一个非线性系统局部区域的局部规则，以局部线性化为基础，通过模糊推理的方法实现全局的非线性。

本文基于引力搜索优化算法(gmGSA)［5－7］辨识T－S 模型的参数，但该算法在优化过程中仍存在早熟收敛现象，易陷入局部最优。为克服标准引力搜索算法中全局搜索能力弱的缺点，本文借鉴遗传算法中基因突变(Genetic Mutations，GM)原理［8］，提出基于基因变异的引力搜索算法，用来辨识T－S 模型的参数。同时利用基于模拟退火［9］和遗传算法的模糊C 均值算法(SAGAFCM)来辨识T－S 模型的结构。该方法辨识出的系统模型精确，且在系统辨识中得到广泛应用。

1 T－S 模型

T－S 模型是一种描述复杂非线性过程的数学模型，可看作是分段线性化的扩展，将非线性系统作为一系列线性系统的加权组合［2］，能将线性控制理论应用到非线性控制系统中。典型的T－S 模糊系统的模糊规则为

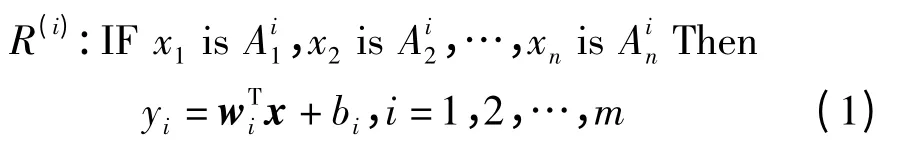
式中，i=1，2，…，m 为模糊规则数;x=［x1，x2，…，xn］为输入量;n 为输入变量x 的维数;w=［w1，w2，…，wn］为n 条规则的参数;yi为第ith条规则的输出;Aij 为模糊子集。若给定输入x=［x1，x2，…，xn］，则最终的输出变量y 可由式(2)计算得到

式中，yi为第i 条规则的输出;μi为第i 条规则的真值;μi(x)为隶属度函数，第i 条规则模糊集的隶属度函数为hi(x)，为各模糊子集的乘积，采用高斯隶属度函数

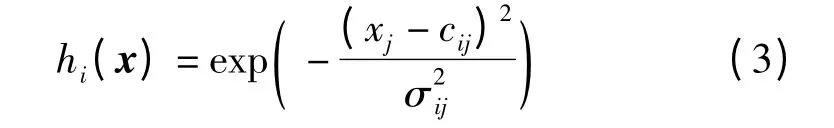
式中，cij为中心参数ci的第j 个分量;σij是基宽参数σi的第j 个分量。

2 引力搜索算法的T－S 模型辨识

2.1 引力搜索算法

引力搜索算法(GSA)［5］是模拟万有引力定律的智能优化算法，在GSA 算法中，种群个体在万有引力的作用下相互运动，个体的位置代表优化问题的解，质量通过函数值计算，解越好质量越大。通过引力作用，个体之间相互吸引并向质量最大的个体方向运动。当搜索结束时，质量最大的个体处在最优位置上，其位置信息对应相应优化问题的最优解。在对最优解进行搜索的过程当中，依靠彼此间力的作用达到优化信息的共享，最终在万有引力的作用下，使得种群朝着最优解所在的区域运动。设有N 个个体存在于D 维空间中，则第i 个个体的位置信息表达式为

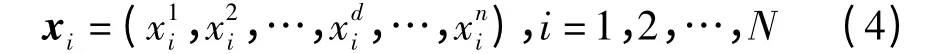
式中，Mai为个体i 在t 时刻的惯性质量;Mpj为个体j 在t 时刻的惯性质量;G(t)为t 时刻的引力因子;ε 为一个恒定的极小值;Rij(t)为物体i 与物体j 间的欧氏距离。则在t 时刻，个体i 在d 维上受到的合力

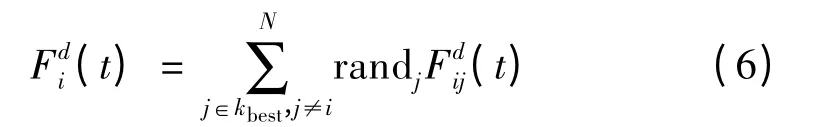
式中，j 是［0，1］范围内的一个随机值;kbest为有引力作用在i 上的个体数量;)表示第j 个个体对第i 个个体在d 维空间上的引力。则在力的作用下，个体i在t 时刻在d 维上得到的加速度为

式中，Mii为第i 个个体的惯性质量。在迭代过程中，个体的速度和位置更新方式如式(8)和式(9)所示。

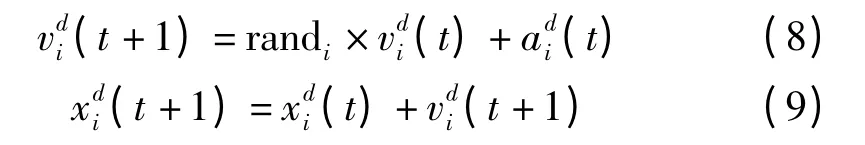
式中，randi是［0，1］的均匀分布。引力因子G 会随着迭代的进行逐渐减小。

通过个体的适应度值来计算其惯性质量的大小，惯性质量相对较大的个体所处的位置较优，其距离最优值也相对较近，该个体对其他个体的力的作用也较大，同时其所获得的加速度相对较小，运动较慢。个体的质量以及惯性质量如式(10)～式(12)所示。

式中，fiti(t)为第i 个个体t 时刻的适应值;best(t)为t时刻最好的适应值;worst(t)为t 时刻最差的适应值;Mi(t)为第i 个体t 时刻惯性质量，对于求最小值问题，best(t)和worst(t)定义如下

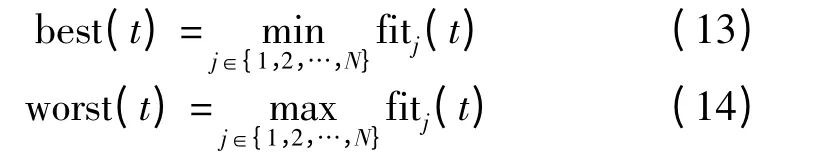
对于求最大值问题，best(t)和worst(t)定义如下

2.2 基于基因变异的引力搜索算法

为克服标准引力搜索算法中全局搜索能力弱的缺点，借鉴遗传算法中基因突变原理，提出基于基因变异的引力搜索算法，即gmGSA，算法在搜索策略上的变化如下:

(1)设变异概率为pr，同时产生一个到之间的随机数，当pr＞pm时，随机产生新个体，否则个体位置不变

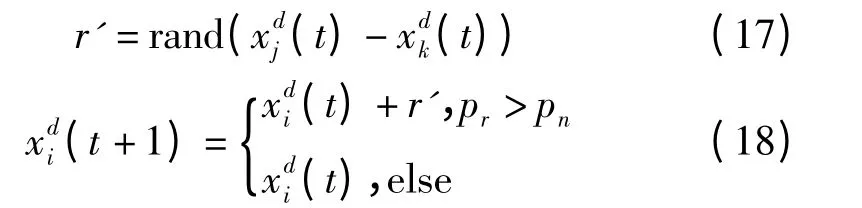
(2)对新个体进行评估，若新评估值fitnew优于原先值fitold，则对个体位置更新到)，否则个体位置不变

gmGSA 搜索方式不同于传统的GSA 搜索方式，增加了一个变异概率，使得种群多样性增加，算法全局搜索能力增强。

2.3 辨识原理

T－S 模型辨识分结构辨识和参数辨识，通常先进行结构辨识，确定规则数及规则中心参数，然后再辨识模型参数。结构辨识中不考虑参数辨识的影响，参数辨识是在已经辨识出的模型结构前提下进行的，不能实现全局优化。本文采用基因变异的引力搜索算法同时确定模型结构和参数，实现模型全局优化辨识。具体方法为:聚类中心的维数为n，m 为指定的聚类数，聚类中的编码如图1 所示。通过引力搜索和基因变异混合优化算法确定类中心，每个类表示一条规则，类中心即为高斯隶属度函数的中心参数ci，同时辨识出的参数还有基宽参数σi，模型的后件参数wi和bi，算法实现简单。每个个体表示一个完整的解ci，σi，wi和bi。个体编码方法如图2 所示。

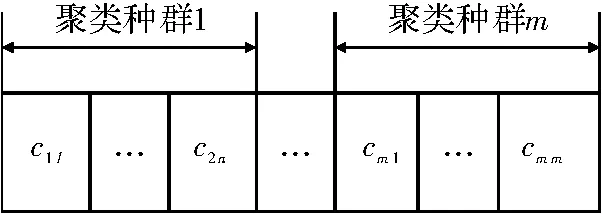
图1 聚类中心编码方法

图2 个体编码方法

假设L 对训练数据(x1，y1)，…，(xL，yL)，采用经验风险最小化方法，训练目标使辨识误差最小

式中，n 为训练样本数;yi和y^i为第i 个输入样本的期望输出和模糊系统输出。

2.4 基于模拟退火遗传算法的FCM 算法

模糊C 均值聚类(Fuzzy C－Means Cluster)算法是一种模糊聚类算法，简称FCM 算法，该算法是一类基于目标函数的聚类算法，通过使目标函数收敛到最小值来达到聚类效果。FCM 算法聚类，原理是用一个隶属关系矩阵U 来表示每个样本点对于每个类的隶属度，矩阵U中每个元素的取值范围为［0，1］，任意一个元素μij表示第j 个样本数据对类i 的隶属度，任意样本点还应满足其对于所有类的隶属度之和为1，假设指定的聚类数目为c，用来聚类的数据样本点为X=x1，x2，…，xn，则

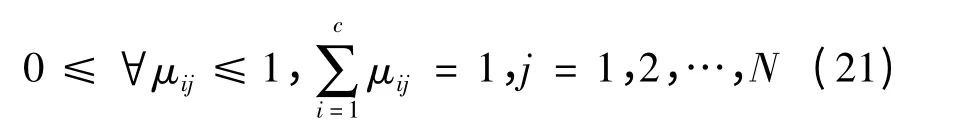
模糊C 均值聚类的目标函数式为

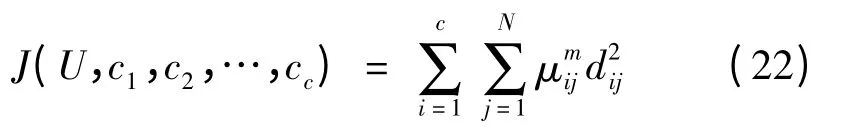
式中，ci为第i 个模糊类的类中心，聚类指数m 的范围为［1，∞］，通常取m=2，当m=1，模糊C 均值聚类变成C 均值硬聚类，为第i 个类中心与第j 个样本点的欧氏距离。

3 仿真实例与分析

这部分分别给出了两个实验来验证gmGSA 算法的辨识精度和经其辨识出的T－S 模型的泛化能力，一个是函数逼近问题，另一个是Box－Jenkins 煤气炉问题。

(1)静态非线性系统。下面是一个具有两输入和一输出的静态非线性系统的表达式

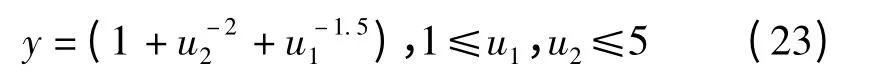
为了比较，取文献［10］中50 组输入输出数据对来做预测测试，设定输入u1和u2随机均匀分布于［1，5］区间。gmGSA 的参数设置成G0=10，β=6，最大迭代次数为500，种群规模为30，模糊规则数为6，辨识参数一共42 个。表1 所示的是前件参数和后件参数的辨识结果。图3 表示T－S 模型辨识的输出和真实系统的输出以及其之间的误差输出曲线图，与其他文献结果比较如表2 所示。

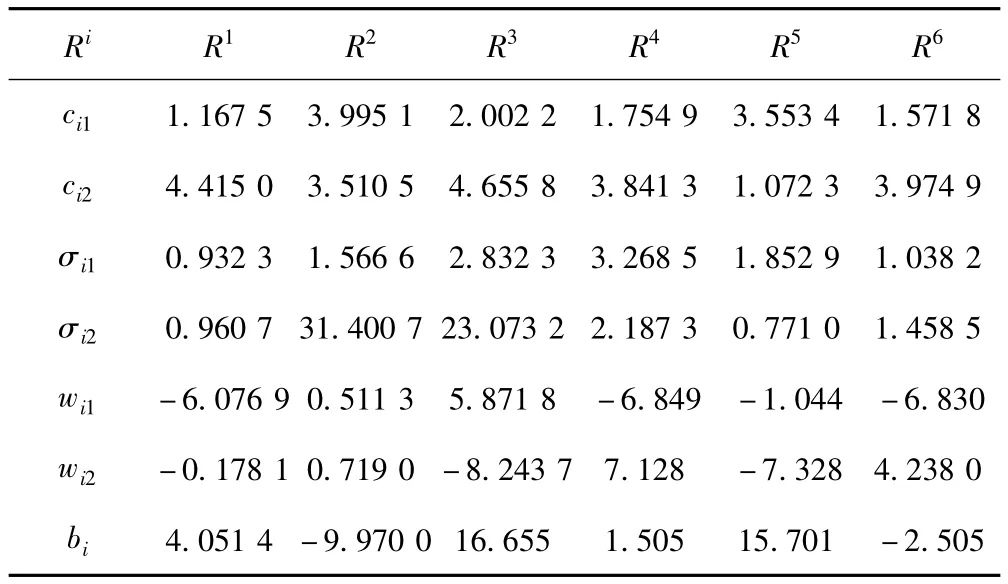
表1 静态函数T－S 模型的辨识参数

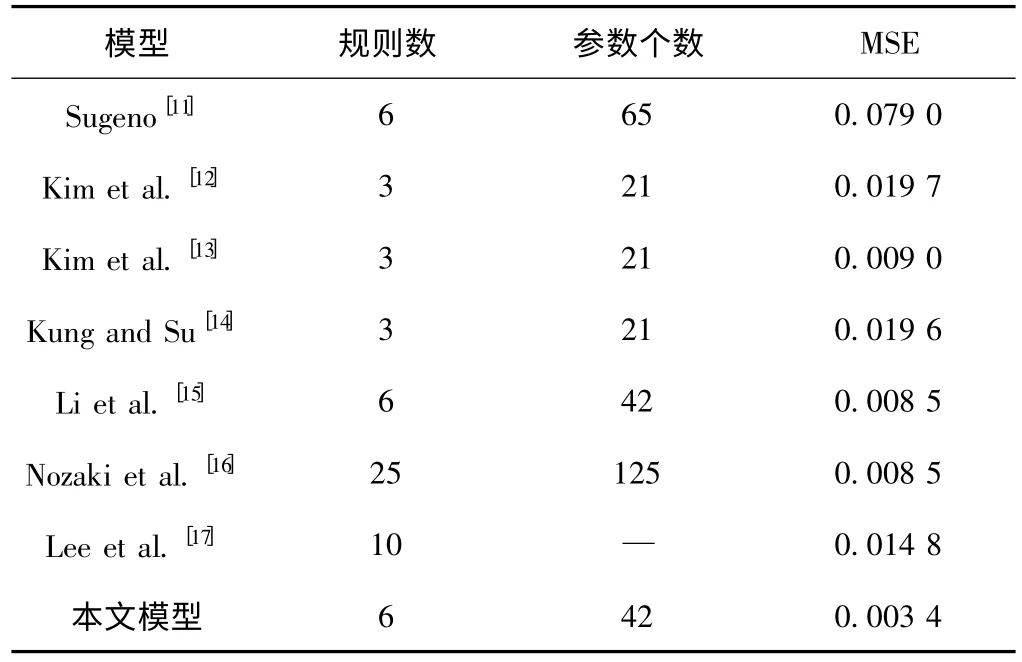
表2 静态函数的辨识结果与其他文献的比较

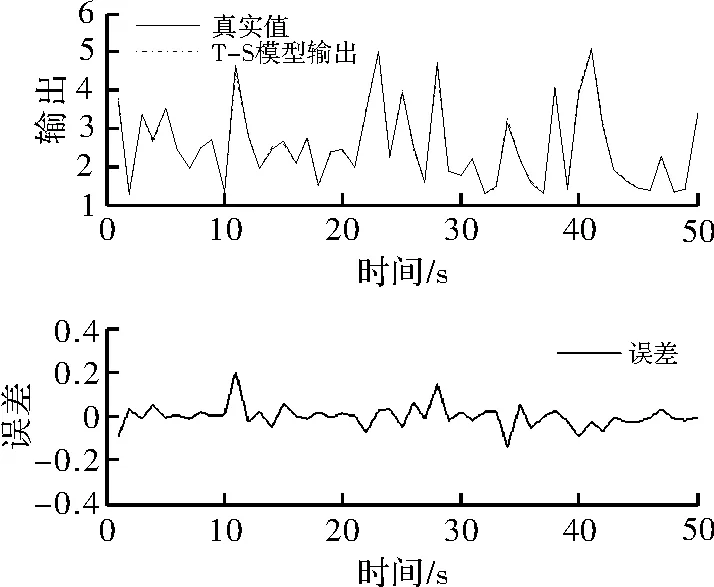
图3 静态非线性函数、T－S 模型及误差输出曲线

在此实验辨识非线性系统问题上，测试的是gmGSA的全局优化能力。表2 显示，gmGSA 算法辨识出T－S模型的均方差为0.003 4，远低于其他文献辨识的结果，证明了gmGSA 算法具有较好的多样性，能够摆脱局部最优值的干扰，最终寻得全局最优值。

(2)Box－Jenkins 煤气炉数据测试。gmGSA 的鲁棒性，再次采用Box－Jenkins 煤气炉数据作为仿真对象。前148 组数据作为训练数据来辨识T－S 模型，后148 组数据则用来测试模型的泛化能力。gmGSA 的参数设置成G0=5，β=6，最大迭代次数为600，种群规模为10。仿真中采用3 条规则，共39 个辨识参数。辨识出的模型参数如表3 所示。

表3 煤气炉T－S 模型参数

样本点和测试点与辨识模型的均方差分别是0.036 和0.101，具体如图4 和图5 所示，与其他文献辨识结果的比较如表4 所示。

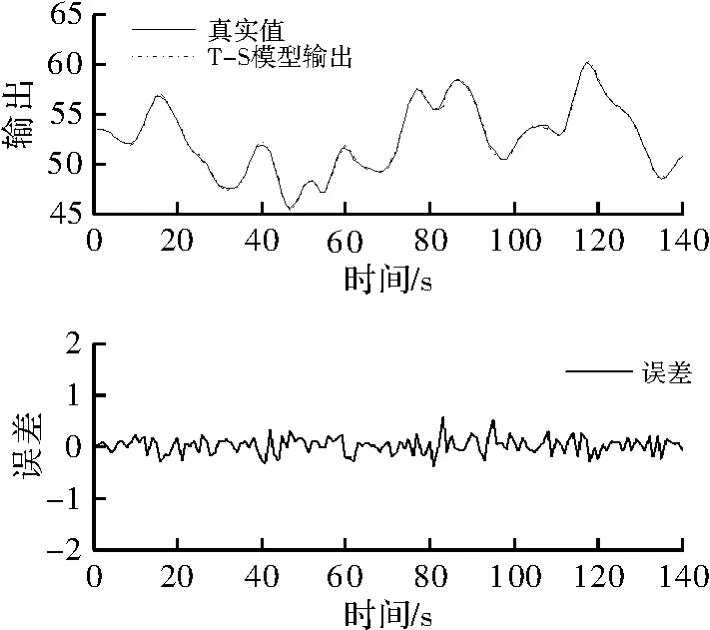
图4 煤气炉样本点、T－S 模型及误差输出曲线

图5 煤气炉测试点、T－S 模型及误差输出曲线

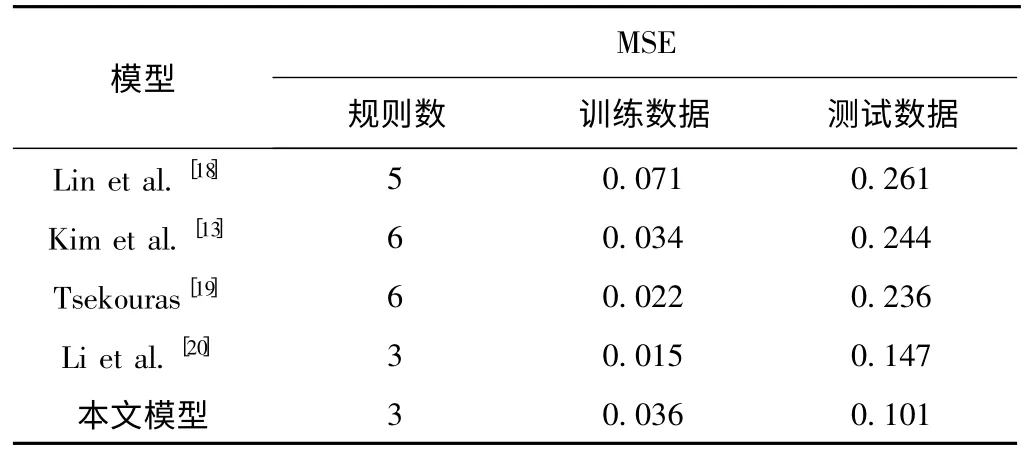
表4 煤气炉辨识结果比较

该实验辨识的是煤气炉数据，主要用来测试用改进算法辨识出的T－S 模型的泛化能力。从表4 中观察，通过SAGA－FCM 聚类和gmGSA 算法辨识出的T－S 模型在辨识精度上较其他文献并非最佳，但已非常接近。重要的是，当用文中所提算法辨识出的T－S模型应用到另一组测试数据时，其表现出了最佳的稳定性和准确性，体现了改进算法辨识出的T－S 模型结构紧凑，且泛化能力强，继而再次证明了改进算法的有效性。

4 结束语

本文主要研究了引力搜索算法，针对标准引力搜索算法易“早熟”的问题，通过分析算法中各个因子的对算法性能的影响，提出改进的gmGSA 算法，通过“变异”来保持粒子的多样性，继而增加粒子种群收敛到全局最优的机会。并应用于T－S 模型的辨识，经实验证明该算法具有辨识精度和较快的收敛速度，以及良好的全局收敛能力，辨识出的T－S 模型结构简单，精度更高，且泛化能力强。

［1］ 吴广玉，范钦义.系统辨识与自适应控制［M］.哈尔滨:哈尔滨工业大学出版社，1987.

［2］ Takagi T，Sugeno M.Fuzzy identification of systems and its application to modeling and control［J］.IEEE Transactions on System，Man，Cybern，1985，15(1):116－132.

［3］ 刘翠.基于T－S 模糊模型的非线性系统辨识［D］.哈尔滨:哈尔滨理工大学，2010.

［4］ Han P，Shi J，Wang D，et al.FCM clustering algorithm for T－S fuzzy model identification［C］.2010 International Conference on Machine Learning and Cybernetics(ICMLC)，IEEE，2010.

［5］ Rashedi E，Nezamabadi－pour H，Saryazdi S.Gsa:A gravitational search algorithm［J］.Information Science，2009，179(13):2232－2248.

［6］ Rashedi E，Nezamabadi－pour H，Saryazdi S.BGSA:binary gravitational search algorithm［J］.Natural Computing，2010，9(3):727－745.

［7］ Srafrazi S，Nezamabadi－Pour H，Saryazdi S.Disruption:a new operator in gravitational search algorithm［J］.Scientia Iranica，2011，18(3):539－548.

［8］ Hedar A，Ali A F，Abdel－Hamid T H.Genetic algorithm and tabu search based methods for molecular 3D－structure prediction［J］.Numer Algebra Control Optim，2011(1):191－209.

［9］ Moret M A，Pascutti P G，Bisch P M，et al.Stochastic molecular optimization using generalized simulated annealing［J］.Journal of Computer Chemstry，1998(19):647－657.

［10］丁学明.基于最小二乘支持向量机的T－S 模型在线辨识［J］.信息与控制，2007，36(4):451－454.

［11］Sugeno M，Yasukawa T.A fuzzy－logic－based approach to qualitative modeling［J］.IEEE Transactions on Fuzzy Systems，1993，1(1):7－31.

［12］Kim E，Park M，Ji S，et al.A new approach to fuzzy modeling［J］.IEEE Transactions on Fuzzy Systems，1997，5(3):328－337.

［13］Kim E，Park M，Kim S，et al.A transformed input－domain approach to fuzzy modeling［J］.IEEE Transactions on Fuzzy Systems，1998，6(4):596－604.

［14］Kung C C.Affine takagi－sugeno fuzzy modelling algorithm by fuzzy c－regression models clustering with a novel cluster validity criterion［J］.IET Control Theory and Applications，2007，1(5):1255－1265.

［15］Li C，Zhou J，Xiang X，et al.T－S fuzzy model identification based on a novel fuzzy c－regression model clustering algorithm［J］.Engineering Applications of Artificial Intelligence，2009，22(45):646－653.

［16］Nozaki K，Ishibuchi H，Tanaka H.A simple but powerful heuristic method for generating fuzzy rules from numerical data［J］.Fuzzy Sets and Systems，1997，86(95):251－270.

［17］Lee S，Ouyang C.A neuro－fuzzy system modeling with self－constructing rule generationand hybrid svd－based learning［J］.IEEE Transactions on Fuzzy Systems，2003，11(3):341－353.

［18］Lin Y，Cunninghaml G A.A new approach to fuzzy－neural system modeling［J］.IEEE Transactions on Fuzzy Systems，1995，3(2):190－198.

［19］Tsekouras G E.On the use of the weighted fuzzy C－means in fuzzy modeling［J］.Advances in Engineering Software，2005，36(5):287－300.

［20］Li C，Zhou J，Fu B，et al.T－S fuzzy model identification with a gravitational search－based hyperplane clustering algorithm［J］.IEEE Transactions on Fuzzy Systems，2012，20(2):305－317.