四旋翼飞行器悬停算法设计与实现

邓博文，窦 强，龚国辉，邓 林

(国防科技大学 计算机学院，湖南 长沙 410073)

四旋翼飞行器与常规飞行器相比，具有机动性高、控制灵活、可垂直起降、自由悬停等特点，近年来成为航空领域的研究热点。早些年，国际上已有诸多科学机构致力于四旋翼飞行器控制技术的研究，并取得良好的成果，具体代表有Draganflyer 公司、宾夕法尼亚大学的HMX4 实验室等。而国内在这方面起步相对较晚［1］。

悬停功能作为四旋翼飞行器独特的动力特性之一，一直是研究的热点及难点。本文通过分析四旋翼飞行器的受力，建立了其在悬停状态下的动力学模型，针对飞行器易受干扰和灵敏度高的特点利用经典PID算法设计了位置控制回路。在Matlab/Simulink 平台上，对模型的悬停模式进行控制仿真，并做了大量现场飞行测试，测试效果良好。

1 数学建模

在对无人机飞行姿态进行控制之前，建立一个合理、准确的数学模型是必不可少的。该模型具有如下约束条件［2］:(1)地面坐标系为惯性坐标系，地球表面视为平面。(2)飞行器为刚体并且质量分布均匀，重心位于机身中央。

人们已习惯将地面坐标系作为衡量物体运动的标准，而飞行器受力分析大多是在其自身坐标系中讨论，因此必须建立机体坐标系与地面坐标系的转换关系，将飞行器的状态转换到地面坐标系中进行分析。如图1所示，建立机体坐标系B(oxyz)及地面坐标系A(OXYZ)。

图1 地面坐标系A 与机体坐标系B

1.1 转换矩阵

坐标系B 到A 之间的变换矩阵R 可写为如下形式［3］

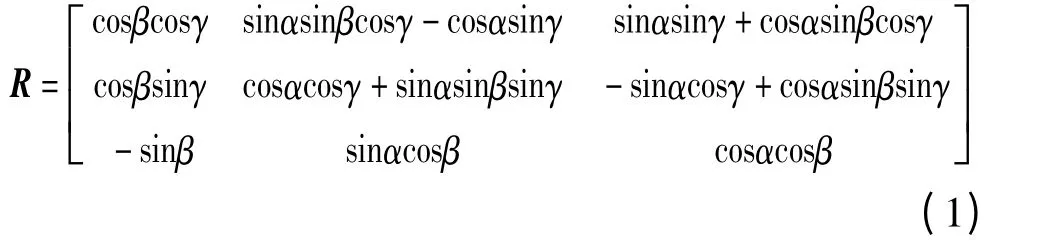
其中，α，β，γ 分别是飞行器在地面坐标系A 中沿OX(俯仰)，OY(横滚)，OZ 轴(偏航)旋转的角度。

1.2 外力平衡方程

在机体坐标系B 中，单个螺旋桨的升力T 和水平转矩τ 与转速存在如下关系［4］

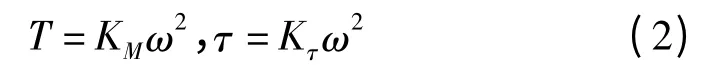
式中，KM为旋翼升力系数;Kτ为旋翼反扭矩系数;ω为旋翼转速。

在机体坐标系B 中，飞行器的升力方向永远竖直向上，结合式(2)，文中将其升力写为

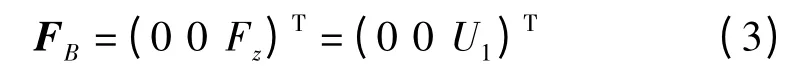
根据转换矩阵R，将飞行器在地面坐标系A 中的升力写成

1.3 外力矩平衡方程

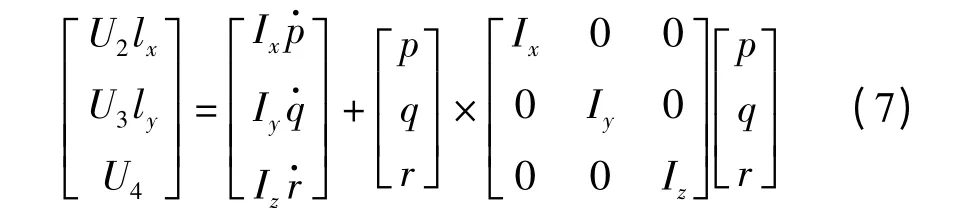
式(8)中，U2=T1+T4－T2－T3，U3=T1+T2－T3－T4，U4=τ1+τ3－τ2－τ4，lx，ly为飞行器绕x，y 轴旋转的力臂长度。根据飞行器结构的对称性，L 为飞行器单个动力轴轴长。

机体坐标系下的角速度［p q r］T与地面坐标系下的角速度［之间有如下关系［6］

由于当角度足够小时，正弦函数趋近与0，余弦函数趋近于1，因此将式(8)简化，可近似地将认为

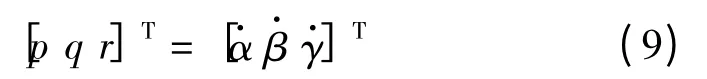
将式(9)的结论代入式(7)，再结合式(5)，得到四旋翼飞行器最终的运动学方程

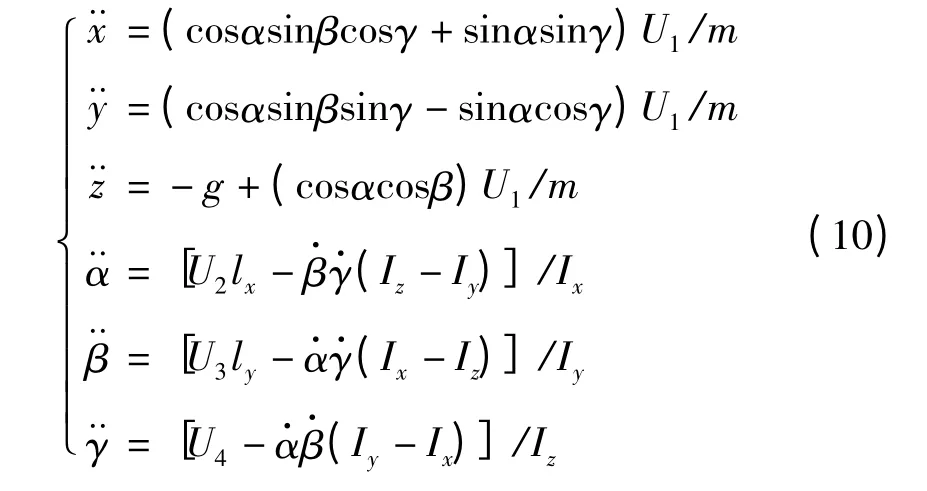
2 控制器设计及仿真

2.1 控制过程

本文针对四旋翼飞行器的特殊动力学结构，分别将姿态、高度和水平位置分开来控制。

如图2 所示，本文将期望得到的坐标值(Ex，Ey，Ez)分别输入到不同的运算单元，计算出期望得到的三轴加速度与姿态角，输入动力单元后分别计算出各个电机的控制量，最后输出飞行器模型，达到控制器飞行状态的目的。

图2 总体控制框架

2.2 PID 控制器

与其他控制方法相比，PID 控制具有结构简单、易于实现、稳定性好等特点。其控制器通过调节比例(P)、积分(I)、微分(D)系数可在满足系统稳定性的前提下达到快速、精确的控制效果［7－9］。鉴于PID 控制和跟踪控制方式的优势，选用PID 控制器可以有效地对悬停这一过程进行控制。

图3 PID 控制器结构

针对图2 中的水平控制器模块和高度控制模块，利用图3 所示结构，通过目标位置与当前位置作差再进行PID 运算［10］，得到3 个运动方向的期望加速度，具体操作如下

式中，(xd，yd，zd)是目标位置的三维坐标;(x，y，z)是当前位置的三维坐标。

2.3 仿真

本文重点是悬停功能的实现，而飞行器只能通过改变姿态角来产生水平方向的加速度。因此，这里重点取姿态控制模块进行分析。

图5 ～图7 分别是俯仰、横滚、偏航的仿真图，实线为期望值，虚线为实际值。当给定输入俯仰和横滚期望角度时(5°)，可看出实际偏转角度存在小幅抖动。但当滚转角和俯仰角趋于稳定时，偏航角迅速收敛回到原点，输出波形的跟随性较好。因此，基于简化模型设计的PID 控制器能够达到较为满意的结果。

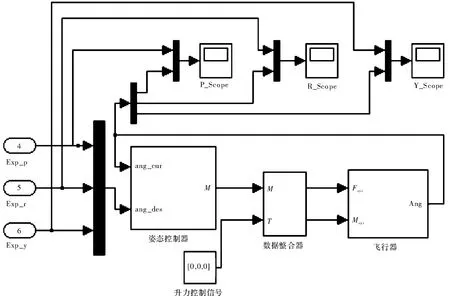
图4 Simulink 中建立的姿态控制模块

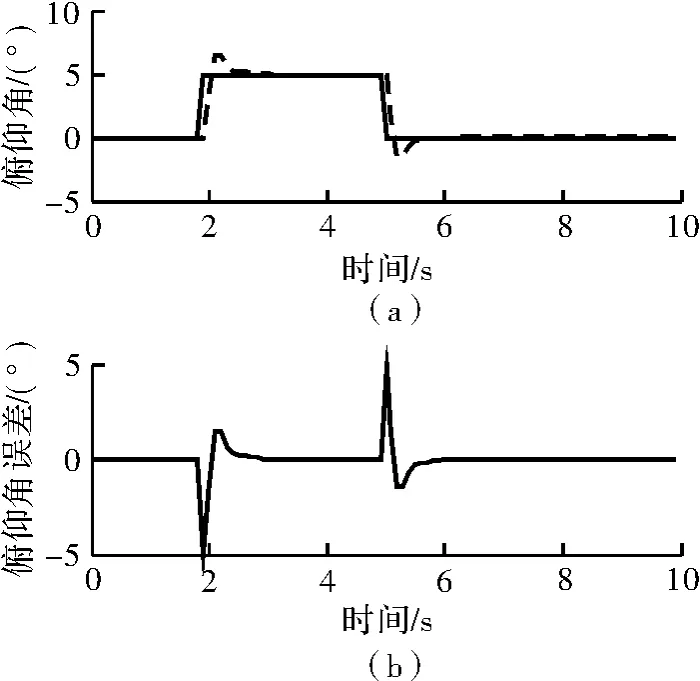
图5 俯仰角仿真波形

图6 横滚角仿真波形

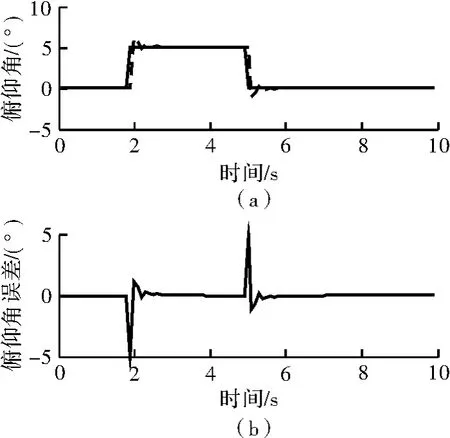
图7 偏航角仿真波形

3 现场飞行测试与结果分析

测试采用机型为轴长0.204 m，中心对称的X 型机架。整机重量为1.34 kg，绕x，y，z 三轴的转动惯量IxIyIz分别为1.968×10－3N·m·s2，1.968×10－3N·m·s2，3.245×10－3N·m·s2。升力系数KM=3.179×10－5N·s2·rad－2，反 扭 矩 系 数 Kτ= 7.432 ×10－7N·s2·rad－2。测试采用激光测距仪记录飞行数据，每次测试时长设定为100 s，每隔1 s 记录一次飞行器数据。其中一组数据如图8 所示。

图8 高度与水平测量结果

在现场飞行过程中，当飞行器起飞至半空，开启悬停功能后，其会在约2 m 的范围内漂移。造成该现象的原因是由于GPS 的精度较低，是无法控制算法弥补的。但观察整个飞行过程，可明显看出，飞行器在漂移达到一定距离时，有明显的回向动作来纠正这一误差，使其飞行位置保持在一个有限的范围内。图8(a)中，飞行器位置落在半径2 m 圆范围内的概率分布达到91%，高度的漂移范围维持在±1 m 以内。

4 结束语

本文以四旋翼飞行器的悬停功能作为研究对象，分析四旋翼飞行器的整体受力情况，建立了近似的数学模型。利用PID 控制方法对飞行器悬停状态下的姿态进行控制，并做了大量现场飞行测试，测试结果为飞行器在水平范围±2 m、垂直范围±1 m 的空间范围内漂移，实现了悬停功能。

［1］ 陈国栋，贾培发，刘艳.微型飞行器的研究与发展［J］.机器人技术与应用，2006(2):34－37.

［2］ 谢木生，王恒升，罗涛.捷联式惯性导航仿真研究［M］.计算机仿真，2013(4):84－88.

［3］ 陈龙.小型四旋翼无人机的自动控制系统设计［D］.成都:电子科技大学，2014.

［4］ 柴卫华，侯芸.捷联惯导系统姿态算法研究［J］.现代防御技术，2001，29(4):43－45.

［5］ 周衍柏.理论力学教程［M］.北京:高等教育出版社，2009.

［6］ 方振华.倾转四旋翼飞行器控制系统设计［D］.哈尔滨:哈尔滨工业大学，2012.

［7］ Karl J Astrom，Tore Hagglund.PID controllers－theory design and tuning［M］.2nd Edition.New York:Instrument Society of America，1995.

［8］ 李波波，贾秋玲.基于滑模控制的四旋翼飞行器控制器设计［J］.电子设计工程，2013，21(16):76－78，82.

［9］ 黄军友.基于PID 控制的X 模式四旋翼飞行器研究［J］.电子设计工程，2014，22(2):127－129.

［10］鄢景华.自动控制原理［M］.哈尔滨:哈尔滨工业大学出版社，2006.