分布式偏好及其在选择中的作用
王志远
(南京大学 现代逻辑与逻辑应用研究所,江苏 南京 210093)
分布式偏好及其在选择中的作用
王志远
(南京大学 现代逻辑与逻辑应用研究所,江苏 南京 210093)
在经典选择理论中无论是接受偏好关系的传递性,还是准传递性,都会导致偏好关系的循环,致使连最基本的选择都无法做出,或出现选择理论与选择实践相反矛盾的情景。分布式偏好是基于传统偏好关系传递性基础上提出的一种偏好关系,给出了分布式偏好的定义、相关定理以及选择条件,对于经典理论中因偏好关系传递性问题引起选择困难的解决提供了一种新思路,解释了个人在选择中出现偏好反转现象依旧能够做出选择的问题。
社会选择;行动主体;认知世界;偏好;模糊偏好;分布式偏好
一、引言
选择依赖于偏好可以说选择的本质就是偏好。偏好被广泛地认为是一种排序,它是建立在行动主体所选规则以及相关背景(包括行动主体的认知状态、情感、倾向、意愿等)的基础上的,分为清晰的与模糊的。无论偏好模糊与否,可以根据截集定理使之清晰化,因此在选择过程中,选择活动本身是清晰的。
由于带有不可比较性关系的偏好结构在经典偏好模型中很少发挥作用[1],通常用两个二元关系来表示方案集X上行动主体的偏好:严格偏好关系P、无差异关系I。这被称为完全性公理。基于X上的偏好结构为R=<P,I>,有xRy=xPy∨ xIy,xPy=xRy∧yRx,xIy=xRiy∧yRx,R满足传递性和完全性,在社会选择中还要求R是非循环的。
Luce给出的反例表明[2],I不具有传递性,从而进一步导致R不具有传递性。设有限方案集X={x1,x2,…,xn},xi为咖啡中加入i粒糖的状态,则有,x1Ix2,x2Ix3,…,xn-1Ixn,进一步有x1Ixn,由于I满足对称性,则xnIx1。由x1Ixn、xnIx1分别可以得出x1Rxn、xnRx1。而Luce等的研究表明x1Pxn[2],即由某人偏好无糖咖啡可知,相对于咖啡中加入n粒糖(例如100万粒糖),他会更加毫不犹豫地偏爱咖啡中加入1粒糖。由x1Pxn可知,x1Rxn和xnRx1成立。这样有x1Rxn∧xnRx1,R不满足完全性。
虽然I会导致P的出现以及R完全性的缺失,迫使一些经济学家弱化原有条件,有理由相信行动主体弱偏好可能不是传递的,而是准传递的[3]。但是,实验社会选择表明,即使是行动主体的偏好关系都P,即放松要求条件,将传递性条件变为准传递性(Quasi-Transitivity),也会导致意料不到的非理性结果。在群选择中,由于准传递性偏好关系的循环性,个体的理性会导致集体的非理性。[4]虽然提供了在传递性循环情况下做出选择的一种能行方法,但这一方法潜在地存在产生新型独裁的可能性,在选择中也会导致非理性的产生。
反例的出现说明了I和P超出了传统社会选择理论的理性范围,许多经济学家探讨了选择中的传递性问题,研究表明,传递性假定并非总是合理的[5],偏好可以是传递的,也可以不是传递的,在选择中,应该允许非传递性偏好关系的存在,甚至是有限的偏好循环[6],以及在社会选择中可以不考虑偏好关系的传递性问题。
正因为偏好关系传递性的破缺,需要重新考察偏好关系的传递性问题,以确保理性因素在选择过程中起主要作用,探究行动主体决策背后的理性原则。在提出并刻画分布式偏好之后,我们基于分布式偏好在选择中的规则、条件,最后探讨分布式偏好在选择中的优缺点。
二、分布式偏好的提出及刻画
社会选择可被表达为群成员偏好到单一群偏好的归约,这样,社会选择可看做是个体选择活动的一种延伸。群选择也是如此,个体选择可以看做是只有一个成员的群选择。
公共知识理论[7]认为,如果P为群中某些成员的公共知识,P→Q是群中另外一些成员的公共知识,则根据演绎规则,Q是群成员的分布式知识(Distributed Knowledge)或分布式公共知识(Distributed Common Knowledge)。这一思想与社会选择理论中偏好关系的传递性在某种程度上是一致的,面临选择时,如果群在群体成员偏好的基础上对方案集{x,y,z}的群偏好为xRy、yRz,则如果不考虑群成员对{x,z}偏好产生的群偏好,那么,依据R的传递性,群体对方案x、y的偏好应是xRz。群偏好xRy和yRz只是依据某种规则,集结群成员偏好的结果,并非在所有的群成员那里都有xRy和yRz。当群成员只有一个时,这时选择成为个体选择或单主体选择,对于方案集{x,y,z},如果行动主体i有xRiy和yRiz,则根据R的传递性,行动主体应该有yRiz。
无论xRz和xRiz,都是由偏好关系的传递性得出的,与直接考察x与z间的关系无涉。由于传统选择理论要求方案间的偏好关系必需满足传递性,则无论群成员有多少个,理论上或实践中都会产生偏好关系的循环,传递性不会被满足。
根据公共知识理论与经典社会选择理论的一致性,我们提出分布式偏好(Distributed Preference),设X={x1,x2,x3,…,xi,…,xn,}为备选方案集,G={1,2,3,…,n}为一群体,R为G的偏好关系(相应地P、I为G的严格偏好关系、无差异性关系),C{X}={xi},i N为G的选择函数;Ri为G成员i的偏好关系(相应地Pi、Ii为G成员i的严格偏好关系、无差异性关系),Ci{X}= {xi},i N为G成员i的选择函数,则有:
定义2.1分布式偏好RD:x1,x2,x3∈X,若x1Rx2且x2Rx3,则x1RDx3;
定义2.2分布式偏好PD:x1,x2,x3∈X,若x1Px2且x2Px3,则;
定义2.3分布式偏好ID:x1,x2,x3∈X,若x1Ix2且x2Ix3,则x1IDx3;
定义2.4分布式偏好RiD:x1,x2,x3∈X,若x1Rix2且x2Rix3,则x1RiDx3;
定义2.5分布式偏好PiD:x1,x2,x3∈X,若x1Pix2且x2Pix3,则x1PiDx3;
其中定义1.、定义2.、定义3.是G的分布式偏好关系定义,定义4.、定义5.、定义6.是行动主体i的分布式偏好关系定义。对G而言,如果G既存在偏好关系xRy,也存在偏好关系yRz,则xRDz为G的分布式偏好;对一行动主体i,如果xRiy且 yRiz,则为i的分布式偏好。xIiDy=。RD和均满足完全性和传统意义上的传递性,即下列各式显然成立:
公理2.1 xRDy∨yRDx;

其中公理2.1、2.1分别为G和行动主体i的完全性公理。
分布式偏好关系是相对于经典选择理论偏好关系传递性(及其计算)的一种偏好关系,它的产生是建立在备选方案集X中方案至少存在3个的基础上。如果备选方案集中方案数目少于3个,则由于备选方案集中方案间关系不满足传递性的一般条件,方案间关系是经典选择理论意义上的偏好关系,分布式偏好不可能产生。
设N(X)为备选方案集X中方案数目,若用RD来分别表示PD和ID,用来分别表示和,则RD、产生的必要条件是当且仅当分别满足:
条件2.1如果RD,则N(X)≥3;
条件2.2如果RiD,则N(X)≥3。
三、基于分布式偏好的选择
根据分布式偏好关系产生的条件、分布式偏好的定义以及传递性的特性,下列各式显然成立:

当经典偏好关系与分布式偏好关系同时存在时,可以依据上述各式进行推导,来确定方案间的偏好关系。
我们称基本的偏好关系为表示性偏好(Expressed Preference),即对于备选方案集{x,y},如果选择群体(或行动主体i)形成偏好关系xRy(或xRiy),则xRy(或xRiy)为表示性偏好。表示性偏好就是传统意义上或经典选择理论中二元对比(Parwise Comparison)形成的偏好关系,其形成的前提条件是备选方案集中方案数目为2。在选择中,如果备选方案集中方案数目大于2,那么由于经典传递性提供了一种便利条件,基于方案所形成的偏好关系,有些是表示性偏好,有些在实质上是我们所定义的分布式偏好。
Luce给出的例子说明[2],对于喜欢无糖咖啡的人而言,x1Ixn是分布式偏好,而不是表示性偏好,表示性偏好与分布偏好出现了不一致。在这类情景下,选择群体或行动主体的最终选择显示,表示性偏好在选择中起关键作用,传统意义上的传递性失去了决定性作用。
在许多情况下,表示性偏好与分布式偏好会出现一致的情况,即:
相应地,可以给出表示性偏好与分布偏好反一致的定义:

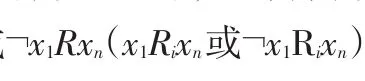
则R与RD是准一致的;
表示性偏好与分布偏好之间关系的最后一种情况是,有x1Rx2∧x2Rx3∧…xn-1Rxn,对于{x1,xn}X,没有形成群偏好,且基于{x1,xn}群中成员存在不同的偏好关系,我们称之为不可断定性关系(混杂性关系)。由于偏好完全性公理,这一情形独特地存在于群成员数目大于等于2的群选择之中,定义如下:
相对于表示性偏好与分布偏好之间关系的反一致性,存在一种只在群选择中出现的弱反一致性,定义如下:
当表示性偏好与分布式偏好一致时,选择的做出与经典选择理论相同的;当表示性偏好与分布式偏好具有准一致性时,虽然做出选择时存在冒险的可能性,但分布式偏好是建立在传递性基础上的,我们认为这种情况与一致性情况是相同的;而表示性偏好与分布偏好不一致时,选择做出的准则是表示性偏好,即根据表示性偏好来确定方案间的偏好关系。与经典选择理论相同,这里也假定选择中群体成员或行动主体是理性的,并且是诚实的。
基于分布式偏好,令X={x,y,z}为备选方案集,对于G而言,C(X)、C|X(xRy)、C|X(xRDy)分别为X上的选择函数、经典选择函数、分布式选择函数,对于行动主体i而言,Ci(X)、Ci|X(xRiy)、Ci|X()分别为X上的选择函数、经典选择函数、分布式选择函数,其值依赖于间x与y的关系,我们给出如下选择中遵循的条件(或规则):
若表示偏示性偏好与分布式偏好具有不可断定性关系时,选择的做出需要构造一个析出函数f,使得f(<RD,x1Rjxn>, xnRkx1)=RD或f(<RD,x1Rjxn>,xnRkx1)=xnRkx1,由于RD与x1Rjxn具有一致性,析出函数可以简写为f(RD,xnRkx1)=RD或f(RD, xnRkx1)=xnRkx1,则C(X)=C(f(RD,x1Rkx1)),该函数的构造依赖群体相关背景。
如果假定选择中群成员是理性的,且具有部分成员对方案的考虑基于知识或高度信念之上,则弱反一致性情景的选择与反一致性情景是相同的,即:
由上述可知,表示性偏好在选择中起着重要作用,分布式偏好只是表示性偏好的一个参考条件,在此基础上,传递性可以被认为是满足一致性和弱一致性的。由于传统理论对二者没有做出清晰的界定与考察,一些情况下能够做出的选择也被视为是存在问题而不能做出的。分布式偏好提供了解决这一问题的可能性,无论是把偏好关系看做是序关系,还是基于效用计算的一种期望效用间的基数关系,分布式偏好的引入能够对选择困难或悖论做出合理解释。
四、结语
依据分布式偏好的定义、公理、定理以及选择条件,选择方案的做出在传统理论的基础上迈出了一步,但由于没有完全考察析出函数在选择中的作用,在一些选择情景中,如果R与RD是不可断定的,选择的做出又会依赖于析出函数的构建,这样,分布式偏好在选择中的作用会显得有些弱化。
[1]De Baets B,de Walle B V,Kerre E.Fuzzy preference structures without incomparability[J]. Fuzzy Sets and Systems,1995(76),333—348.
[2]Luce R D. Semiorders and a theory of utility discrimination[J].Econometrica,1956(24),178—191.
[3]Armstrong W E.Utility and the theory ofwelfare[J]. Oxford Economic Papers,1951(3),259—271.
[4]Wang Z Y.Existence ofsatisfied alternative and the occurring of Morph-Dictator[A]. Proceedings of International Workshop on Logic, Rationality, and Interaction(LORI-II)[C].Heidelberg:Springer-Verlag, 2009.
[5]May K.O.Intransitivity,utility and the aggregation of preference patterns[J].Econometrica,1954(22),1—3.
[6]Schwartz T.Rationality and the myth of the maximum[J]. Noûs,1972(2),97—117.
[7]Roelofsen F. Distributed Knowledge[J]. Journal of Non-classical Logics,2006(16),1—18.
责任编辑 吕学文
(E-mail:dalishi_sohu@sohu.com)
B81 < class="emphasis_bold">文献标识码:A
A
1007-905X(2010)04-0093-04
2010-04-23
江苏省规划项目(08ZXB002);国家社会科学基金项目(09BZ015);江苏省普通高校研究生科研创新计划(CX09B_002R)
王志远(1974— ),男,河南襄城人,南京大学现代逻辑与逻辑应用研究所博士研究生。

