谈数学“探究式”课堂教学

尚召雪

摘 要:探究性活动始发于问题,推进于问题,发展于问题,不仅以问题为起点和线索,而且最终也应以问题的提出为归宿,帮助学生推广、引出新的结论和新的问题,使学生的探究能力进一步提高。

关键词:探究式学习;数学课堂教学构建;应用

中图分类号:G633.6 文献标识码:A 文章编号:1009-010X(2009)07-0052-02

“探究式”教学的特点是以“学生活动和问题研究”为中心,引导学生自主探究新知,弘扬学生人格主动精神,挖掘学生创新潜能,促进学生个性全面发展,以《三角形的中位线定理》教学为例,操作程序如下:

一、创设问题情境,诱导学生发现结论,激发探究欲望

(1)怎样测量操场中被一障碍物隔开后两点A、B的距离?如图1小明测量的方法是:在AB外选一点C,连AC、BC,取AC、BC的中点M、N连MN,量出MN=20m,这样能得出AB的长吗?AB与MN有何关系?你猜测AB与MN的关系是①_______②_______

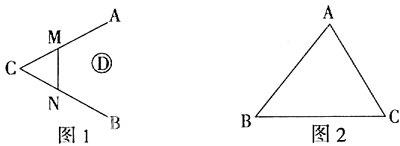
(2)MN这条线段既特殊又重要,我们把它叫做△ABC的中位线,即连结三角形两边_____点的线段叫三角形的_____

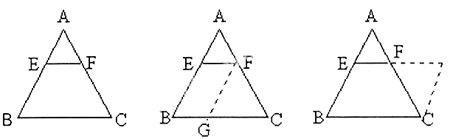
(3)一个三角形有____条中位线,画出如图2的所有中位线,观察测量发现

( )∥( ),( )=( );

( )∥( ),( )=( );

( )∥( ),( )=( );

用语言叙述上述结论,三角形的中位线_______并且___________

(4)画出图2的△ABC的中线,它与中位线有何区别?

说明:①以上内容让学生按印发的学习提纲在课前完成。

②三角形中位线定义的引入、定理结论课本是直接给出的,为了强化学习动机,变“要我学”为“我要学”,让学生通过实验操作,观察比较,估计猜测,自己发现结论,这样可培养学生对数学的内在兴趣,让学生认识到数学不是少数天才创造的,而是经过努力一般人都可以发现的,而又是解决实际问题的有力工具,符合从“感性到理性”的认识规律。

二、创设思维情境,启导学生发现证明结论的思路和方法,培养学生创新思维能力

(1)检查课前自学情况,教师提问有关问题和方法,学生回答,并用多媒体展示答案。

(2)教师指出同学们观察发现的这些结论是否正确,还需严格证明。教师板书,学生在提纲上写出已知求证。

(3)启导全体学生思考,讨论证法,教师巡视与学生一起研究,收集信息,了解情况。

说明:①本题与以前学过的哪些知识、方法有关?是什么关系?学生进行联想、回答。②怎样证一条线段等于另一条线段的一半?学生回答:截(把长的平分)与补(把短的加倍)。经过探讨,学生不难发现三种证法。③定理的证明,不拿现成的方法给学生,而是创设思维情境,启导学生“联想”到学过的有关知识和方法,使新知识得到顺利同化,并引导学生展开讨论,实现思维交锋,智力碰撞,这大大激发了学生的求知兴趣,让他们体验到成功的喜悦,数学思维能力在这一过程中得到了有效的发展。

三、释疑解惑,引导学生独立完成证明,培养逻辑推理能力

(1)要求A组同学选做一种证法,B组同学选两种证法,C组同学三种证法都做,尖子生能发现新的证法或问题。(2)两人板演。(3)教师巡视,注意帮助学困生,并收集有关信息。

说明:传统教学的证明过程都是由教师完成,这不符合主体性原则,既然学生已知道怎样解,就应让学生独立完成,加大学生的参与度,对提高学生的独立表达能力有好处,使学生体验到成功的欢乐。

四、精讲总结,理性归纳,使学生形成新的认识结构

(1)教师引导学生分析定理的特点,题设两个“中点”结论“平行”“一半”。

(2)再指出:凡是与“中点”“平行”“线段部分”有关的问题可考虑使用此定理。

说明:帮助学生揭示定理的本质特征,为灵活运用定理作准备。

五、精心设计练习,进行变式训练,使学生在运用知识中形成技能,培养学生迁移与创新的能力

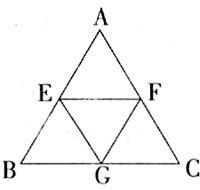
(1)引导学生观察下图可发现哪些新结论?让学生抢答。

注意:简单的结论先让A组或B组同学回答,不明显的结论让C组同学补充,给各类学生提供表现才能的机会,并及时给予表扬与鼓励。

结论:3个平行四边形,4个小三角形全等,小三角形的周长为原三角形的一半,面积为原三角形的四分之一,这些结论很重要,若学生没全部找出,可稍加提示。

(2)这个问题能否进行推广?若△ABC改为四边形ABCD,又发现什么结论,如图,让学生抢答,原则同上,结论有EFGH为平行四边形,EG与FH互相平分,四边形EFGH的面积为ABCD的一半等。

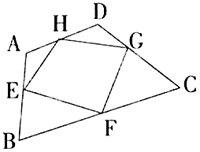
(3)学生思考如何证明四边形EFGH为平行四边形。

教师启导:①由条件“四边的中点”可联想到什么知识,是否有三角形的中位线?②EF是哪个三角形的中位线?FG、GH、HE呢?学生马上意识到要连“对角线”。

(4)抢答:让三个学生先后口述证明(证法不同)过程,教师板书或用多媒体演示。

(5)教师指出:三角形中位线定理的两个结论可选用一个或两个都用。

(6)变式训练。①若四边形ABCD是平行四边形,矩形、菱形、正方形、等腰梯形,则四边形EFGH分别是______、______、______、______、______。②为使四边形EFGH是平行四边形、矩形、菱形、正方形,则原四边形ABCD必须满足什么条件?教师用《几何画板》在计算机上拖动一个顶点让四边形进行变化,学生观察发现结论,教师问其理由。③引导学生总结规律:四边形EFGH的形状是由什么决定的?(AC与BD,而与四边形ABCD形状并没有直接联系)

说明:①把课本练习3与例1两个孤立的问题结合在一起,体现了数学知识之间的联系,用联系、变化的观点去研究各问题之间的转化,展示给学生一个动态的知识“先后”过程,促进学生新认识结构的形成与发展。②把它们改编成开放性问题,让学生有更广阔的思维空间,提供一个有利于群体交流的活动环境,让师生思维双向暴露,符合活动性原则。③再次体验研究数学的思想方法。

六、课堂小结(以问题形式进行)

(1)教师引导三角形中位线定理能否进行推广?

(2)若把三角形改为四边形,是否也有中位线?哪些四边形有中位线?有什么性质。

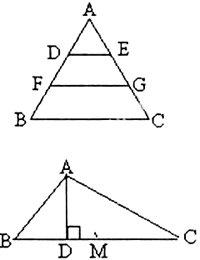
(3)若把三角形的中点改为三等分点

D、F与E、G分别是AB、AC的三等分点,

则DE FGBC之间存在关系?

(4)请同学们看提纲的作业补充思考题,让学生思考,教师作启导。

①M是BC的中点,可联想到哪些

知识。(学生:三角形中线、中位线、

直角三角形斜边中线等)

②教师:有没有符合三角形中位线定理的条件?学生:没有,欠一中点。

③教师:怎么办?学生再取一个中点(AB、AC上)

说明:采用两个思考题进行小结,打破传统小结方法,这是因为①三角形中位线定理及结论、难点是如何创造性地应用。②把定理进行引伸,让学生余味未尽,带着问题,并为下节课研究“梯形中位线”做好铺垫,一举两得。

以上6步是基本的操作程序,不是固定不变的,应根据不同的教学内容和学生情况及教学环境的变化而灵活运用,步骤可增加或减少,但以学生活动与问题研究为中心的基本思想不能变。

【责任编辑 姜华】