初中二次函数教学中PBL模式的运用

【摘要】文章探讨如何有效地运用PBL（问题驱动学习）教学模式进行初中二次函数教学设计。首先，文章介绍PBL模式的含义及教学设计的原则；其次，阐述在初中二次函数教学中运用PBL模式的教学过程，包括复习导入、创设情境、设置任务、小组合作、汇报展示和评价反馈等；最后，得出结论：PBL模式在初中二次函数教学中的运用能够有效促进学生合作学习和问题解决能力的发展。

【关键词】PBL模式；二次函数；初中数学

随着社会的发展和教育理念的变革，传统的教学模式已经不能满足学生的需求。PBL模式作为一种以问题为驱动的教学方法，强调激发学生的主动性，能够培养学生的综合能力，满足学生的发展需要。下文就如何在初中二次函数教学中运用PBL模式开展深入探讨。

一、PBL模式的介绍

（一）PBL模式的内涵

PBL，即基于问题的学习（Problem-Based Learning），是一种颠覆传统教学理念的新型教育方法。其核心在于将学习聚焦于解决实际问题，通过问题驱动的方式来引导学生主动学习，提升学习能力。在PBL模式中，问题的设定是至关重要的。问题不仅是学习的起点，还是学习的导向。它能有效激发学生的好奇心和求知欲，促使学生主动探究，明确自己的学习需求和目标。同时，问题的多样性、开放性和真实性，也为学生提供了广阔的学习空间和实践机会，使学习更加贴近现实，更具实际意义。另外，PBL模式强调以学生为中心。在这一模式下，教师不再是知识的灌输者，而是学生学习的引导者和陪伴者。学生则需要通过自主学习、合作探究、信息搜集和整合等方式来解决问题、获取知识。在这一过程中，学生的自主学习能力、创新思维能力、团队协作能力等都会得到显著提升。总之，PBL模式是一种以学生为中心、以解决实际问题为导向的新型教学理念和方法。它不仅能有效激发学生的学习兴趣和动力，还能全面提升学生的学习能力和综合素质，是现代教育发展的重要趋势之一。

（二）PBL模式中驱动问题的设计要点

一方面，驱动问题应具有真实性，能连接现实与学习场景。在PBL模式中，驱动问题的设计需紧密贴合学习者的生活环境和兴趣领域，确保其真实性。这种设计有助于学习者将所学内容与现实生活紧密结合，形成深刻的印象，从而增强记忆和理解效果。真实的驱动问题能让学习者更好地认识到学习的实际价值，激发学习的主动性。另一方面，驱动问题应具有开放性，能拓展思维与探究空间。驱动问题的开放性是PBL模式的重要特征之一。这类问题往往没有固定的答案，允许学习者从不同的角度和层面进行探究和思考。学习者在解决问题的过程中，需要运用各种知识和技能探索多种可能性，最终找到合适的解决方案。

二、PBL模式的教学设计原则

在运用PBL模式开展教学设计时，教师必须遵守一系列核心原则。

第一，问题中心导向原则。此原则系PBL模式的灵魂所在。问题的设定需真实且具有挑战性，能够激发学生的求知欲望与探索热情。问题的构思要与学生的既有知识体系及技能储备相匹配，同时紧扣学习目标，确保学生能在解决问题的过程中实现知识与技能的双重提升。

第二，贴近生活实际原则。该原则强调问题设计需与学生的日常生活及未来发展紧密相连，使学生能够从实践中领悟知识的实际价值。将理论知识与生活情境相结合，不仅能够激发学生的学习兴趣，还能帮助他们更加深入地理解并掌握所学知识，从而将抽象的理论转化为具体的实践，增强实践能力。

第三，有效协作互助原则。PBL模式鼓励学生之间建立积极的合作关系，共同面对问题并寻求问题解决方案。学生们可以集思广益，通过在小组内充分沟通和协商，共同商讨出最佳的解决方案。这种合作方式不仅能够培养学生的团队合作精神，还能让他们学会在集体中发挥自己的特长并承担相应的责任。

第四，多元评价结合原则。此原则要求教师在评估学生的学习成果时，需采用多元化的评价方式。评价内容应涵盖学生的知识掌握程度、技能运用情况、思维方式及社交能力等多个方面。同时，教师应采取过程性评价，以便及时给予学生反馈与指导，确保学生能够获得显著的提升与进步。

PBL模式教学设计原则的运用，有助于构建一种以学生为中心、以问题为导向的教学模式。在这种模式下，教师不再是单纯的知识传授者，而变成引导学生探索问题、解决问题的引路人。这样的教学方式不仅有助于激发学生的学习兴趣和主动性，更能培养他们的批判性思维、团队协作能力和解决实际问题的能力。同时，这些教学设计原则也为教师提供了明确的教学思路，从而使教师可以更好地把握教学节奏，确保学生在探究问题的过程中能够实现成长和进步［1］。

三、在初中二次函数教学中应用PBL模式的教学过程

第一，教学导入阶段：创设挑战性问题情境。课堂伊始，教师设计了一个与二次函数相关的、具有挑战性的问题：“如何根据抛物线的形状和位置写出二次函数的表达式？”这样的问题既能激发学生的兴趣，又能引导他们深入思考二次函数的性质。

第二，制订目标阶段：明确探究方向。在抛出问题后，教师引导学生明确学习目标，包括理解二次函数的性质、掌握列二次函数表达式以及运用二次函数解决实际问题的方法等。在具体的学习目标的指引下，学生能够有针对性地开展探究活动。

第三，问题探究阶段：小组合作，深入探索。教师按照学生的能力划分小组，每组3到6人。在小组合作中，学生们需要共同搜集资料、讨论问题、建立假设，并通过实验、计算等方式验证假设正确与否。在此过程中，教师应及时提供指导和支持，帮助学生解决遇到的困难。

第四，分享反馈阶段：交流成果，互相学习。各小组将探究成果进行展示和分享，包括发现的规律、得出的结论以及解决问题的方法等。其他小组可以提出问题和建议，共同完善探究成果。同时，教师应对学生的表现进行点评和反馈，帮助他们进一步加深对二次函数的理解。

第五，解决问题阶段：应用知识，解决问题。在掌握了相关知识和技能后，学生们开始尝试用二次函数解决一些实际问题。通过解决问题，学生能够进一步巩固所学知识，并提升应用能力。

第六，总结评价阶段：反思过程，提升能力。最后，教师引导学生对整个探究过程进行总结和评价。学生应反思自己在探究过程中的表现，包括思维方式、学习策略等，找出自己的不足和需要改进的地方。同时，教师应对学生的表现和成果进行评价，肯定他们的努力和进步，并提出建设性的建议。

四、初中二次函数教学中PBL模式的具体应用

（一）复习导入，调动旧知

课堂开始，教师进行导入：“同学们，我们已经学过了一次函数的概念，哪位同学能来为我们回顾一下？……很棒，你的回答非常完整且流畅。但同学们，你们想过吗，不是所有问题都能用一次函数解决。今天，我们将一起深入探究二次函数，看看它是如何为我们打开新世界的大门的！”

（二）创设情境，设置任务

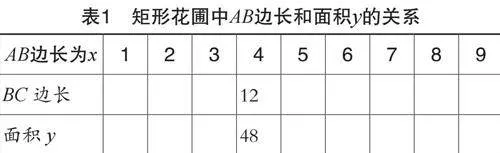
教师创设以下情境—在园林设计中，矩形花圃是一种常见的布局形式。其简洁的线条和规矩的形态，不仅易于施工和维护，还能有效地利用空间，展现出优雅与和谐的视觉效果［2］。今天，我们就将通过一个具体的实例，来探讨矩形花圃的周长与面积之间的关系。假设有一个矩形花圃，其周长为32米，两边分别为AB和BC。为了简化问题，我们设AB边的长度为x米，矩形的面积为y平方米。请你在表1中填写AB边长与面积y的关系。教学过程中，教师不断提出问题、设置任务，如“请同学们思考，x的取值范围有限制吗？”“你能用x和y表达函数关系式吗？”等。

此环节的设计，旨在让学生在解决实际问题的过程中逐步领略数学的奥妙和价值。在此过程中，由于学生初次接触二次函数这一概念，因此，当学生尝试根据所给情境写出函数表达式时，难免会面临诸多困惑与挑战。这种困惑是一种宝贵的教学资源。它能够有效激发学生的好奇心和求知欲，使他们带着问题去学习，从而更加深入地理解二次函数的本质和特性［3］。

（三）小组合作，完成任务

首先，小组讨论，分析共同特征。教师借助多媒体屏幕呈现了四个函数解析式，并布置任务，请学生观察屏幕上的函数解析式，发现其共同特征。学生需开展小组讨论，与同伴相互交流、探讨，并填写小组讨论记录表。

其次，回顾对比，揭示函数关系。教师提问：“请你通过对一次函数特征的分析，比较其与新函数的共同点与不同点。”通过对比，学生能够更清晰地认识到二者之间的共同点和不同点，从而加深对函数关系的认识。学生通过观察和比较可以发现，这些函数虽然都存在一个未知数，但在未知数次数方面却存在差异。比如，一次函数的未知数次数为一次，而新函数的未知数次数则为两次。这种发现让学生对新函数的特性有了更加深入的理解。

再次，命名解释，深化概念理解。教师进一步提问：“你能在上述问题的基础上为这些函数进行命名并解释命名原因吗？”这一环节旨在引导学生深入思考函数的本质特征，提升他们的推理能力，同时培养他们的创新思维。此外，学生还需解释命名的理由，这进一步检验了他们对一次函数和二次函数概念的掌握程度［4］。

最后，总结概念，提升认知层次。教师引导学生尝试根据一次函数的概念，总结二次函数的概念。这一环节旨在帮助学生将所学知识进行归纳和整合，形成对二次函数概念的完整认识。学生在回顾一次函数知识的基础上，对一次函数与二次函数的特性进行了细致的对比，为理解二次函数概念奠定了基础。在分组探究环节，学生积极投入，充分利用教材及其他学习资源，通过互相交流、协作的方式，对二次函数的定义及特征进行了深入探讨，逐渐加深对二次函数的认识。

（四）汇报展示，评价反馈

在成果展示环节，教师挑选几位小组代表上台，让他们总结和分享自己小组在学习探索过程中的成果与心得。学生要详述各自小组是如何逐步深化对二次函数定义和特征的理解，并得出最终成果的。同时，学生还要分享小组成员在合作与交流过程中遭遇的难题及采取的解决措施。在授课结束之际，教师带领学生再次回顾本堂课的核心知识，总结关于二次函数定义、特性及规律的关键性结论，以帮助学生巩固所学，完善知识结构。

这一环节旨在帮助学生巩固和深化对二次函数的认识。此外，为了激发学生的自主学习动力，教师进一步引导学生开展自我评价，并与同伴相互评价。这不仅能促使学生反思自己的学习态度、方法和成效，还能帮助他们从他人身上汲取经验，进而提升自我。在这一过程中，学生通过认真聆听他人的经验，并与自己的成果和做法进行对比，来不断完善自己的思维方式和学习策略。通过组内互评及自我评价，学生不仅对自己的学习过程进行了全面的审视，还吸收了同伴的经验。这一环节的设计体现了教学评价的多元化。

结语

通过将PBL模式引入初中数学教学，二次函数教学从传统的以教师为主导的模式转变为以学生主动参与为主的模式，学生能够更深入地理解二次函数的意义，掌握运用二次函数解决问题的方法。因此，初中数学教师可借助PBL模式提高学生的合作学习和问题解决能力。

【参考文献】

［1］陈美娟.巧用PBL模式实施初中数学教学：以“二次函数中的最值问题”为例［J］.名师在线，2024（6）：83-84.

［2］王学勤.基于PBL模式的初中数学单元教学策略思考［J］.数理天地（初中版），2023（15）：50-52.

［3］蔡春艳.基于PBL模式的初中数学教学思考：“二次函数”第一课时课堂实录与思考［J］.中学数学，2022（20）：29-31.

［4］李忠琴.初中数学PBL教学模式应用策略研究［J］.理科爱好者（教育教学），2020（1）：75-76.

作者简介：张丽芬（1974—），女，福建省漳州市南靖县湖美中学。