运用多种解题策略,提高小学数学学习效率
顾春晓

摘 要:小学数学教师需强化解题策略的指导,通过多种策略的指导和引导深化学生对解题策略的认识,使学生在训练中成为有效的问题解决者,提高数学学习的效率.为此,教师应在教学的过程中不断渗透转化策略、画图策略、假设策略和列举策略,才能让学生在解题过程中感受数学的魅力,感悟数学思想,提高数学学习效率.
关键词:转化策略;画图策略;假设策略;列举策略
解决问题的过程是学习知识的过程,也是创造性分析和思考的过程.学生只有掌握了一定的解题策略,才能在解决实际问题时快速而正确地解题.[1]那么,如何训练和培养呢?
1 转化策略
大量实践表明,转化策略有利于各种类型问题的解决,对学生思维的发展也是十分有利的.因此,在教学的过程中,教师需从具体教学内容出发,有针对性地渗透转化思想,指导学生借助转化策略解决问题,以提高解题能力,增强数学应用意识.[2]以“一道分数应用题”的探索为例.
案例1
首先,教师用PPT呈现学校各个兴趣小组活动的真实场景.
师:瞧,同学们活动得真开心啊!我们来看看合唱兴趣小组,小组中男生有27人,女生人数占总人数的47,有多少女生?
师:这个问题你们会解决吗?(学生陷入思考,五分钟后依旧探寻不到问题的切入口)
师:你们脑海中有没有一些想法可以提出呢?
生1:如果从分数和比之间的关联性出发,将这里的分数“47”转化为比,那么是不是就有思路了呢?
师:生1的这个提议非常有价值,那我们就来试一试吧.从题目条件“女生人数占总人数的47”可以得出什么?
生2:女生人数与总人数之比是4∶7.
生3:也就是说一共有7份,其中女生人数占据4份,那么男生人数就占据3份.
生4:根据占3份的男生人数是27人,就可以求出每一份的人数是“27÷3=9(人)”;进一步得出占4份的女生人数是“4×9=36(人)”.
师:多么漂亮的解题思路!
可见,本例题中教师借助了现实情景引出数学问题,利用学生的喜闻乐见,引导学生思考并探寻出“转化思想”的策略.此时,学生脑海中的转化思想并不清晰,只知道需要通过转化思想来思考并降低问题难
度,化抽象的分数问题为简单的按比分配问题.在后续问题的解决过程中,学生充分经历了思考、猜测、探索、讨论、思辨等过程,脑海中的解题策略一步步由模糊变得清晰,创造性地完成了解题,同时思考力和创造力得到了渐进式发展.[3]
2 画图策略
小学生的心理处于形象思维为主的阶段,实物或图形等直观材料可以有
助于
学生的数学学习.而画图形象直观,可以直观诠释题意,是小学生解决复杂问题最基础的策略.因此,当学生面对无从下手的难题时,教师可以适时指导学生运用画图策略,有条理地表示数量间的关系,让问题获解,让思路变清晰.以“长方形和正方形的周长和面积”的问题为例.
案例2
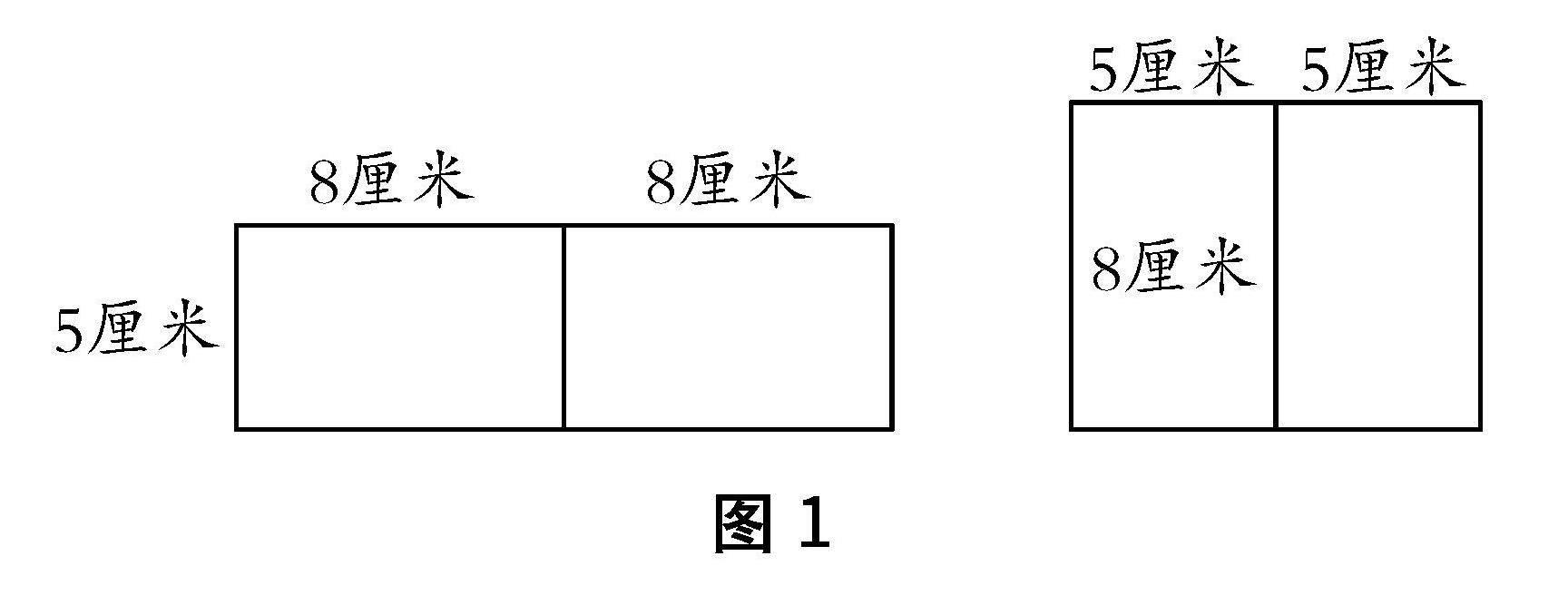
问题:将两个长为8厘米、宽为5厘米的大小相同的小长方形拼成一个大长方形,试求出拼出的大长方形的周长与面积.
师:你打算如何解决本题?
生1:这个问题很简单,我可以先算出一个小长方形的面积和周长,再将其乘2就能得出结果了.
师:生1说得有没有道理?其他人也赞同他的方法吗?(其他学生陷入沉思)
师:我们是不是可以换一种方法和思路来解决问题,比如画出这个图形看一看它是什么样子的.(学生在教师的引导下立刻画出了图1,并主动标出了已知条件)
图1
师:现在你能发现什么?
生2:拼出的大长方形的面积是2个小长方形的面积之和,但周长不是.
师:现在会解决本题了吗?
生(齐):会.
小学阶段的学生思维十分活跃,需要教师好好加以指引和点拨.画图策略从本质上来说就是数形结合思想的展现,可以使复杂问题简单化、形象化,让问题迎刃而解.以上案例中,生1出现错误认知的根源在于受到思维定势的束缚.面对这样的错误,教师没有直接抛出正确的答案,而是引导学生借助画图策略去探寻正确的解题方法.学生也没有因此而气馁,而是在教师的指导下勇往直前,从数与形的本质联系出发,画出图1所示的图形,使问题获解.这样的
活动过程将画图策略的价值充分展现,为学生提供了复杂问题方向的指引,为解决抽象数学问题打好了
基础.
3 假设策略
假设是一种常用的思维模式.一般情况下,当直接推理法无法帮助学生探寻到解题突破口时,教师可以采用假设策略进行尝试,让题目中隐蔽的数量关系明朗化,从而实现快速、正确解题.因此,教师应从实际教学内容出发,精准运用假设策略解决数学问题,通过问题的解决让学生感受假设思想的应用,从而掌握并乐于运用这种策略.
案例3 明明有10元钱,且都是1元和5角的硬币,共13枚,那么1元硬币有几枚?5角呢?
师:大家试着去解决本题.(学生思考未果)
师:大家看,老师这里有13枚1元的硬币,我们将它代替问题中的13枚硬币,现在是多少钱?
生1:13元,比题目多3元.
师:为什么会多3元?
生2:因为这里的13枚中不全部
都是1元的,也有5角的.
生3:将1枚5角硬币替换为1元硬币就多了一个5角,而此时多了3元,则有5角=0.5元,3÷0.5=6(枚),这就说明其中有6枚5角硬币,则有13-6=7(枚)1元硬币.
师:非常棒哦!还有其他思路吗?
生4:我们是不是还可以将所有1元硬币都假设为5角呢?
师:非常不错的想法.那我们就来算一算……
以上案例中,教师抛出一个看似简单却让学生望而却步的问题,激发了学生的认知冲突.教师又给出实物让学生感受到假设策略的应用价值,从而进一步激起他们深度探索的欲望,最终完成假设策略的应用.
4 列举策略
所谓“列举”,就是将所有可能性一一罗列出来,那么数学解题中的列举策略就是在一一罗列之后,有序地整理以获得问题的答案.列举策略在数学解题中具有较高的应用性,可以提升学生
解决
问题
的能力.因此,教师需从学生的身心发展特征出发,以解决
问题
为中心,有效开展列举策略解题的训练,从而让学生在条理思考中进行思维碰撞,收获数学知识,掌握解题方法,培养数学思维.
案例4 王大爷想要围一个长方形的花圃,他现有22根1米长的木条,你觉得怎么围才能让王大爷拥有一个面积最大的花圃呢?
师:请大家在读题后深入思考该如何围呢?(学生展开分析)
生1:我试了很多方法,可无论如何调整,这个花圃的周长都是22米,长、宽之和都是11米,还都是整米数.
师:那么如何才能找出一个面积最大的围法呢?
生2:我们可以借助手边的小棒试一试.(学生自发地进行操作)
生3:长6米,宽5米.
生4:长9米,宽2米.
生5:长7米,宽4米.
……(教师一一板书学生的结论)
生6:这样你一种我一种的,好多围法都重复了,而且太乱了,根本没办法得出结果.
师(追问):那么有没有一个好方法来整理一下这些数据,让它们既不重复又不遗漏呢?
生7:我觉得可以试一试列表整理.
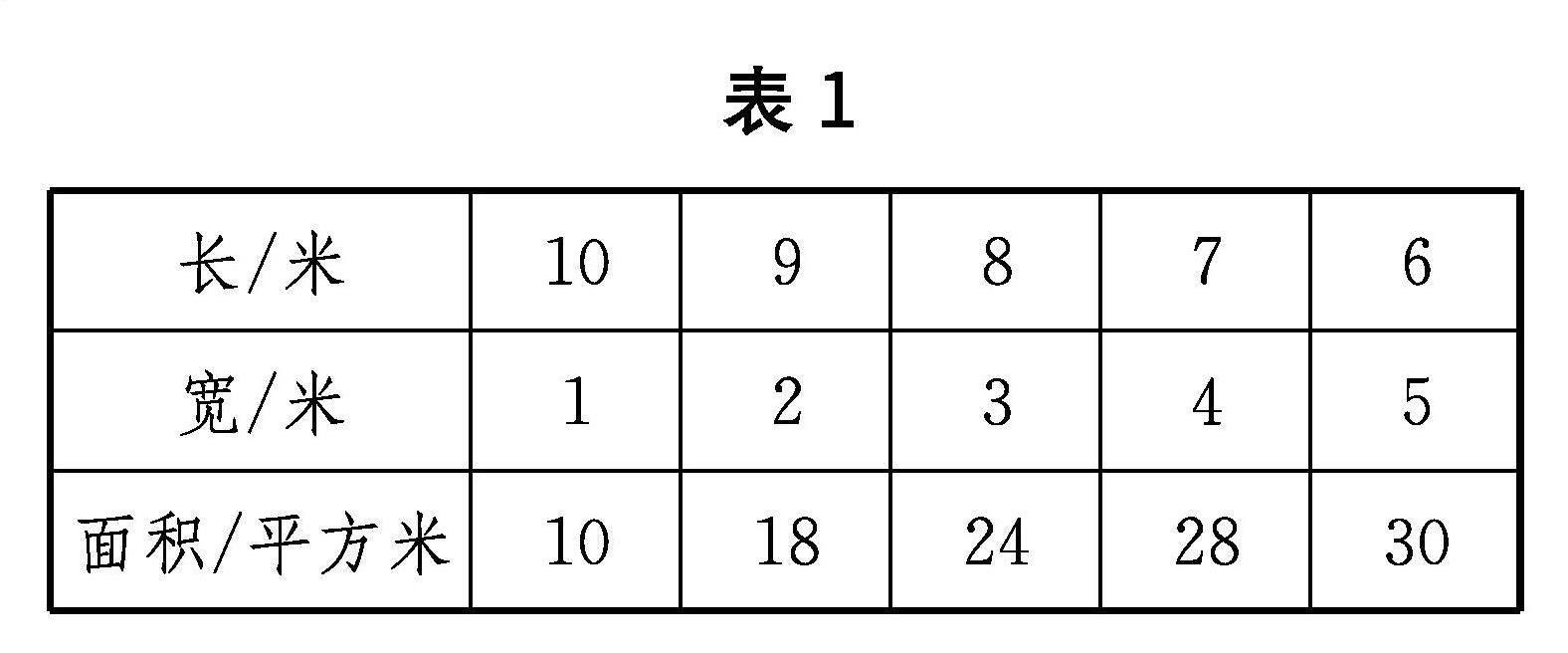
师:不错!我们来试一试吧!(学生很快制作出表1)
表1
长/米109876
宽/米12345
面积/平方米1018242830
师:这种解题的策略就是一一列举,那么观察表格后你发现了什么?
生8:长与宽长度越接近,所围花圃的面积就越大.
……
以上案例中,教师抛出问题后给予了学生足够的时间和空间,有效激发了学生对于列举策略的需求,让他们在思考、操作、对比的过程中获得深刻的列举感受.可以说,正是有了这样有层次的活动设计,才使得列举策略的优势得到了充分展现,从而将知识转化为能力,提升了学生思维的有序性和灵活性.
总之,在教学中,教师不仅需要让学生理解、掌握和运用这些常用解题策略,还需要让学生领略解题策略的多样化,来不断优化学生的解题技能.只有注重优化和运用解题策略,才能让学生在解题中感受数学魅力,感悟数学思想,提高数学解题能力和数学学习效率.
参考文献
[1]罗雪如.小学数学问题引领式教学的应用研究[J].试题与研究,2022(16):110-112.
[2]冯厚笠.高中数学教学中发展学生创造性思维的策略[J].新课程(教研),2011(1):60.
[3]齐永虎.数学解题中的“转化”[J].池州师专学报,2003,17(3):89-90.

