一道平面几何最值问题的多种解法
冯兴旺
【摘要】解三角形中的最值(或取值范围)等问题,场景新颖,知识交汇融合,技巧方法众多,是全面考查学生“四基”与能力的重要题型之一.文章基于一道平面图形翻折的模拟题的创设,以解三角形的最值问题来合理设置,从角参与边参的设置,以及坐标构建等多思维视角切入,巧妙解决相应的解三角形的最值问题,拓展数学思维,提升数学品质,引领并指导数学教学与解题研究.
【关键词】解三角形;翻折;函数;导数;不等式
引 言
解三角形中的最值(或取值范围)等问题,是近几年新高考数学试卷命题的一个热点,问题背景灵活多变,知识考查面广.特别是在新高考数学试卷中,此类问题有时还巧妙融入现实生活、数学文化等应用场景,成为一类创新性的综合应用问题,倍受各方关注.对其解题方法与技巧进行探究与总结十分必要.
一、问题呈现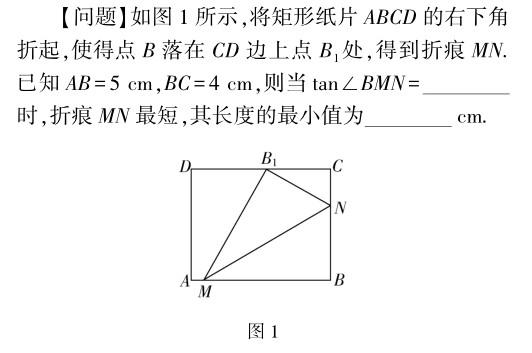
本题是一道以平面图形翻折为背景的平面几何的最值问题,此类问题主要考查正弦定理、余弦定理、不等式等相关知识,以及平面几何、三角函数等知识.在解决此类问题时常用到平面几何、三角函数、解三角形、不等式、函数与导数的应用等相关知识,此类题有一定的综合性,并且对代数变形能力要求较高,综合考查直观想象、逻辑推理以及数学运算等核心素养.
根据该问题的实际应用场景,解题者可以从角参设置与边参设置等不同思维视角切入,合理构建对应的关系式,通过关系式的结构特征,利用函数思维或不等式思维并结合相关知识来分析与解决问题.
二、问题破解
(一)角参设置思维


解后反思 根据应用场景引入边参来合理构建所求线段长度的关系式,也是解决问题时比较常用的一类技巧.以边参为参数(注意对应的取值范围)所对应的函数,可以通过函数的本质,利用函数与导数的应用来处理与转化,这往往是解决与之相关的最值(或取值范围)等问题中最为常用的思维方法.
(三)坐标构建思维
方法4(导数法3)
解析 以A为坐标原点,AB,AD所在直线分别为x轴、y轴建立平面直角坐标系,

解后反思 根据平面几何图形的结构特征,将其放置于平面直角坐标系中,通过平面几何与平面解析几何的交汇来综合应用.合理引入点的坐标、直线的斜率等参数,巧妙构建所求线段的长度关系式,进而通过函数与导数的应用、重要不等式的应用等来确定对应的最值问题,从而实现问题的突破与解决.
三、教学启示
(一)命题设置方式,知识综合交汇
综合性的解三角形问题可以很好地考查学生的数学基础知识、数学思想方法与数学能力等.而处理解三角形问题往往可以利用平面几何图形来打开思路,这是近年各地高考模拟卷中解三角形问题的一个基本模式,在高考命题也必将占有一席之地.
此类解三角形问题求解的方法通常引入合理的角参或边参,结合平面几何图形的特征,综合解三角形的相关定理、性质、公式等构建关系式,通过对应的函数、不等式等知识来分析与解决问题.
(二)思路方法归纳,技巧能力提升
解决此类解三角形问题的一般思路主要包括以下两种:
(1)代数角度,寻找关于角或者边的函数或不等式关系,进而从函数或不等式视角来分析与求解.
(2)几何角度,借助平面几何知识,寻找图形中蕴藏的几何关系,从直观想象与数形结合视角来分析与求解.
当然,解决此类解三角形问题经常采用的思路是代数与几何的综合,从几何中寻找关系,进而合理构建代数关系,对代数运算与几何推理加以综合应用,分析与解决问题.
结 语
此类平面几何图形翻折成对应平面几何图形的创新应用问题,要正确把握翻折过程中变与不变的量(涉及边、角等),通过合理的参数引入来构建对应的关系式,进而将几何问题代数化,解决此类解三角形问题.
【参考文献】
[1]朱小成.等腰三角形中不确定性问题的解决[J].中学数学,2023(24):64-65.
[2]罗培洲.高中数学中三角函数的解题技巧:以三角函数的图形与性质为例[J].数理化解题研究,2023(30):50-52.
[3]王东海.由2023年高考题谈解三角形中三线问题的破解策略[J].中学生理科应试,2023(12):14-16.
[4]沈鸿羽,顾予恒.探究“一破二”模型,破解三角形问题:以2023年高考题为例[J].中小学数学(高中版),2023(Z2):15-16.

