立足境脉教学，促进素养落地

唐婷婷

摘  要：境脉教學既包括问题情境、教学流程的脉络，也包括学习者认知结构关系发展的脉络.通过情境的脉络发展关系把课堂的教学任务有机结合起来，学生主动使旧知与新知发生联系，组织建构认知结构，并使之成为其自身知识网络的一部分.

关键词：境脉教学；核心素养；直线与平面垂直

《普通高中数学课程标准（2017年版2020年修订）》指出高中数学课程要以学生发展为本，要优化结构、突出主线，要启发思考、把握本质.在数学教学中，教师不仅要按照数学学科特点组织教学，更要尊重学生的已有经验，帮助学生建立新的学习脉络.教学活动从“教”走向“学”，从“累积知识”走向“涵育素养”，“境脉教学”由此诞生.

1  境脉教学的内涵特征

境脉教学中的“境”即教学情境，“脉”即教学主线.境脉教学既包括问题情境、教学流程的脉络，也包括学习者认知结构关系发展的脉络.主题情境作为教学主线贯穿首尾、前后呼应，通过主题情境的脉络发展关系把课堂的教学内容有机结合起来，学生主动地使旧知与新知建立关系、发生意义，组织建构认知结构，并使之成为其自身知识网络框架的一部分.

2  基于核心素养的教学设计

本文设计了突出学生主体地位并具有互动生成的教学情境，通过问题驱动衍生出学生自主探究的教学活动，落实了学生的知识与技能，提升了学生的核心素养.

2.1

教学目标设置

（1）通过观察实例，说出直线与平面垂直的定义.

（2）借助直观感知、探究类比、操作确认，得到直线与平面垂直的判定定理并会作出解释.

（3）体会空间问题平面化、线线垂直与线面垂直的相互转化.经历合作探究，构建并完善知识结构.

2.2

教学重点难点

教学重点：直线与平面垂直的定义和判定定理的理解及应用.

教学难点：操作确认并概括出直线与平面垂直的判定定理.

2.3

教学过程设计

教学活动1  温习旧知，先验新知接境

问题1  请同学们回顾直线与平面的位置关系有哪些？我们已经学习了直线与平面平行的定义、判定、性质，大家想一想，接下来我们要学些什么呢？

【设计意图】获取研究对象，明确“为什么学”.

问题2  通过类比“直线与平面平行”的学习过程，你认为要具体研究“直线与平面垂直”哪些方面的内容？需要采取什么研究方法？按怎样的过程进行研究？

【设计意图】研究“直线与平面垂直”这部分内容，其本质是研究两类不同维数空间基本图形的位置关系，引导学生找到与其具有类似结构的“直线与平面平行”进行类比，设计切实可行的研究思路，让学生进一步明确“学什么”“怎么学”.在研究过程中，教师需引导学生挖掘内隐的思想方法：“降维”“平面化”.

教学活动2  引入情境，创设任务启境

问题3  我们都知道，研究一类数学对象的起点是定义.那么，应该怎样对“直线与平面垂直”下定义呢？

追问  你能发现生活中直线与平面相交的例子吗？

【设计意图】克莱罗在《几何基础》中对直线与平面垂直的定义：“一条直线不向平面的任何一面倾斜，则直线与平面垂直.”图1，图2中比萨斜塔的“斜”，旗杆的“直”，说明生活中处处存在着直线与平面的斜交与垂直交，鼓励学生体会生活中的数学，用数学的眼光观察世界.

问题4  观察阳光下垂直于地面的旗杆，随着时间的推移，旗杆影子所在的直线也在不断地变化.如图3，旗杆AB所在的直线与它的影子所在的直线垂直吗？那么，旗杆AB与地面内不经过点B的直线也会垂直吗？为什么？

追问  你能尝试给直线与平面垂直下定义吗？

【设计意图】学生能根据实际问题情境抽象概括出直线与平面垂直的定义，即“若一条直线垂直于平面上与该直线相交的所有直线，则该直线与平面垂直”.这与欧几里得《几何原本》中线面垂直的定义不谋而合.此时，教师引导学生进一步观察，学生不难发现，对于平面内不过点B的任意一条直线B′C′，总能在平面上找到过点B的一条直线与之平行，根据异面直线垂直的定义可知AB⊥B′C′.因此，AB垂直于平面内的任意一条直线.进而，学生自主完善直线与平面垂直的定义，即“若一条直线垂直于平面内的任何一条直线，则直线垂直于平面”.

教学活动3  回归定义，学习脉动入境

问题5  我们除了可以用定义来判断直线与平面垂直，还有其他稍微简便一点的方法吗？

追问1  通过观察实物模型，如图4，翻开一本书立于桌面，此时书脊AB与桌面是什么关系呢？通过直观感知，思考只要满足“什么条件”，就能使直线与平面垂直.

追问2  可以通过怎样的实验来进行操作确认呢？请大家分小组完成相关操作.

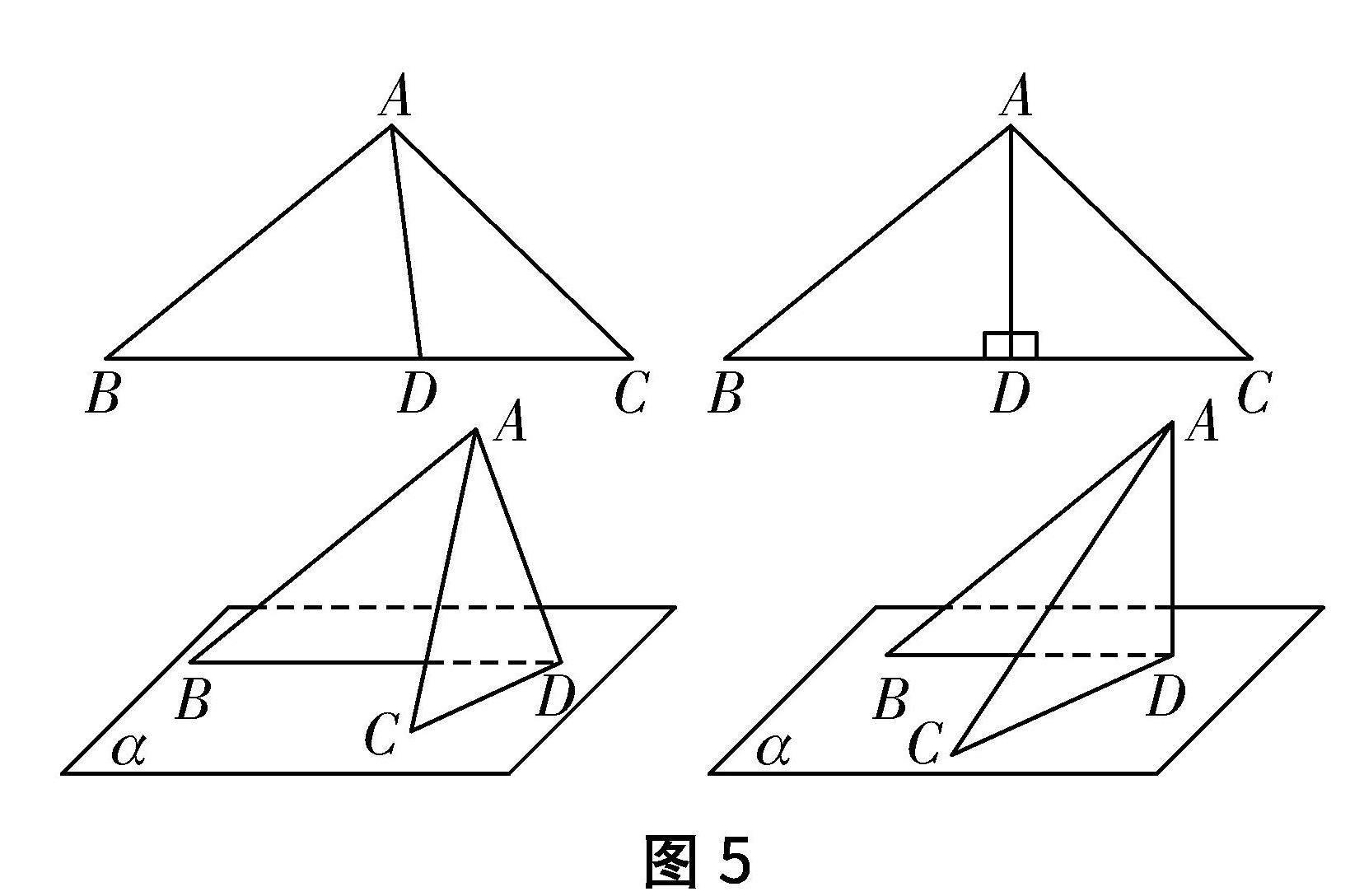
学生活动：图5中，折纸操作，过△ABC的点A翻折纸片，得到折痕AD，将翻折后的纸片竖起置于桌面，验证折痕AD与桌面是否垂直.

追问3  类比直线与平面平行的判定定理的叙述方式，你能得出直线与平面垂直的判定定理吗？

【设计意图】类比直线与平面平行的判定定理，即将“直线与平面的平行”问题转化成“直线与直线的平行”问题，体现了“降维”和“平面化”的思想方法.学生自主归纳直线与平面垂直的判定定理，即“如果一条直线与平面内的两条相交直线垂直，那么直线与该平面垂直”.通过基本事实的推论2，学生想到：两条相交直线可以确定一个平面，两条平行线也可以确定一个平面.

教学活动4  解决问题，形成联动生境

问题6  求证：如果两条平行直线中的一条直线垂直于一个平面，那么另一条直线也垂直于这个平面.

【设计意图】培养学生将文字语言转化为图形语言和符号语言的能力，用数学的思维思考，用数学的语言表达，引导学生养成从定义和判定定理寻找问题突破口的习惯.

变式  在《九章算术》中，刘徽曾多次提到阳马、鳖臑等几何模型.文中将底面为长方形且有一条侧棱垂直于底面的四棱锥称为阳马，将四个面都为直角三角形的四面体称为鳖臑.在四棱锥P-ABCD中，侧棱PD⊥底面ABCD，且PD=CD.试判断四面体P-BCD是否为鳖臑，并证明.

【设计意图】学以致用，学生通过体验成功，不断激发学习兴趣.通过变式题，融入了数学文化，让学生体会中国古代文化的博大精深.学生通过情境、学境、心境之间的境相交融，不断优化知识框架结构.

教学活动5  反思小结，建立脉络出境

为什么学（研究的背景）？学什么（研究的内容）？怎样学（研究的脉络、思想方法）？你认为接下来学什么（尝试新的探究）？

【设计意图】教师鼓励学生从基础知识、基本方法、核心素养三个方面自主总结，并用流程圖辅助展示本节课外显的探究历程、内隐的思想方法.引导学生注重经验关联，学会迁移应用、举一反三、适度拓展，进而建立新的学习脉络.

3  基于核心素养的境脉教学策略分析

境脉教学的原则是坚持设计为先、立足学生、实施为要、植根学习.情境性、探究性、脉络性是其主要特征，落实核心素养是其根本目标.

3.1  引入情境脉络，让新知生成有理有据

通过挖掘生活素材，构建情境境脉.教师选择贴近学生实际的旗杆和影子的情境设计教学活动，驱使学生自主探究，主动优化直线与平面垂直的定义，促使新知后形成有理有据.

3.2

围绕活动脉络，让课堂教学更具厚度

本节课通过类比直线与平面平行的判定定理的形成过程，学生通过直观感知、探究发现、操作确认，得到“一条直线垂直于一个平面内的两条相交直线即为直线与平面垂直的判定定理”，符合学生的最近发展区.在判定定理的形成过程中，教师不断引导学生感受探究过程中“降维”“平面化”的思想方法，做到课堂教学简约而不简单，还数学以思维的本质，使数学课堂更加丰满、厚重，让学生享受其中.

3.3

形成知识脉络，让素养脉络根植课堂

形成知识脉络，即要求教师将知识的演绎结构转化为学生的认知结构，纳入学生已有的知识体系，为形成新知奠定基础.学生利用已有的知识经验，从知识境脉、经验境脉中提取自己所需要的学习内容，自主建构数学新知.通过本节课的学习，学生在情境中尝试解决问题，在经历中学会了直线与平面垂直的判定方法，在经验中进行了迁移运用，通过不断完善自身知识结构，为接下来学习直线与平面垂直的性质定理做好铺垫，从而多维度提升经验建构的深度体验.

境脉教学有利于学生深度理解和剖析数学学习的内容和本质，真正意义上从“教师的教”转向“学生的学”，从“知识的学习”转向“本质的体悟”，从“数学知识累积”转向“学科涵养化育”.境脉教学给师生带来了更多经验建构、解决问题、学习成长的契机和路径，在潜移默化中促进学生的数学核心素养落地.