MATLAB软件辅助高等数学教学

郑洪清

关键词： MATLAB 函数 定积分 高等数学

中图分类号： G642;O13-4 文献标识码： A 文章编号： 1672-3791（2024）01-0182-04

高等数学作为理工类本科生的一门公共基础课，具有知识点繁多、内容抽象和计算复杂等特点，再加之学时受限，导致众多学生对该门课程学习效果较差。因此，在高等数学授课过程中，如何展示知识点的应用场景、抽象内容可视化、复杂计算简单化和激发学生的学习兴趣和动手能力是每位教师必须思考的问题。已有多位学者将MATLAB 软件辅助高等数学教学的研究［1-4］和提升学生能力的研究［5-6］，这些研究基本上都是调用MATLAB 软件的自带函数进行求解，而对函数的内部实现机制并未探讨，这样会导致有的学生对有些概念比如定积分的定义理解不透。尤其对计算机类专业学生来说，如何利用代码理解定积分的“分割取近似，求和取极限”的这一过程是学习的一个难点。本文将探讨对计算机类专业学生来说如何使用MATLAB 软件辅助高等数学学习，主要展示某些知识点在计算机中的应用场景以及如何利用定义自行编写代码求解定积分，此举不仅使学生体验了知识点的应用场景，还激发了学生的学习积极性和动手能力，同时也培养了他们利用专业知识解决数学问题，实现学科的交叉融合，达成学以致用之目的。

1 MATLAB 展示函数的应用场景

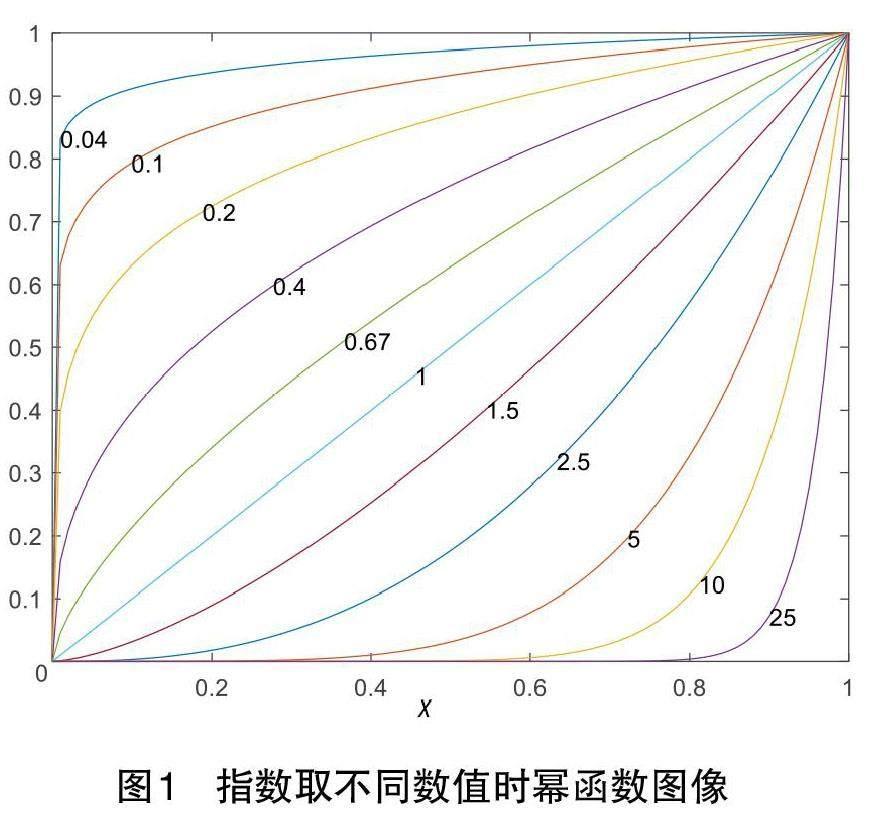
在高等数学的第一章分别介绍了分段函数、反函数、复合函数和初等函数等，这些函数大都在中学时期都已经学过。传统的教学方法通常展示函数图像并介绍其性质，对其应用场景涉及甚少，学生在学习过程中感觉枯燥乏味，浮光掠影。而利用MATLAB 软件教学则可以呈现知识点的具体应用场景，例如：在讲解幂函数y = x^a 时，可以通过MATLAB 软件形象展示其指数取不同数值时函数的图形，如图1 所示。

在MATLAB 软件中编写如下代码便可实现上述图像。

%利用MATLAB 绘制幂函数图像

x=0：0.01：1；%声明变量x，且指定x 的范围从0 到1，间隔为0.01

r1=［0.04，0.1，0.2，0.4，0.67，1，1.5，2.5，5，10，25］；%声明指数变量并指定其取值

xx=0.01：0.089：1；

for i=1：length（r1）

plot（x，x.^r1（i））；%画幂函数图形

hold on；%连续绘制

text（xx（i），xx（i）.^r1（i），num2str（r1（i）））；%标注指数及位置

end

那么该函数在现实问题中有何具体应用呢？为拓展其应用范围和激发学生学习兴趣，将其应用于灰度图像的增强处理。

例1 利用幂函数应用图像2，注意观察指数取不同数值时图像效果的变化情况。

从图2 和图3 的效果图可知，指数取不同数值时图像对比度完全不同，当指数为1.1 时图像效果对比度显著增强；当指数为0.9 时图像效果对比度明显变暗。让学生直观感受原来简单的幂函数还有灰度图像增强或减弱作用，大大激发了学生学习乐趣。对于其他分段函数和对数函数等都可以仿照该方式进行教学，体会学以致用。

在MATLAB 软件中编写如下代码便可实现灰度图像增强或减弱效果：

img=imread（'Fig_einstein_low.tif'）；%导入图像

a1=1.1；%指数值

a2=0.9；%指数值

［r，c］=size（img）；%获取图像的行列

img1=double（img）；%将图像数值转换为双精度

for i=1：r

for j=1：c

img2（i，j）=img1（i，j）.^a1；%计算幂函数值

img3（i，j）=img1（i，j）.^a2；%计算幂函数值

end

end

subplot（1，2，1）；

imshow（uint8（img2））；

title（'指数a=1.1 时'）；

subplot（1，2，2）；

imshow（uint8（img3））；

title（'指数a=0.9 时'）；

2 MATLAB 在定积分中的应用

2.1 一元函数定积分

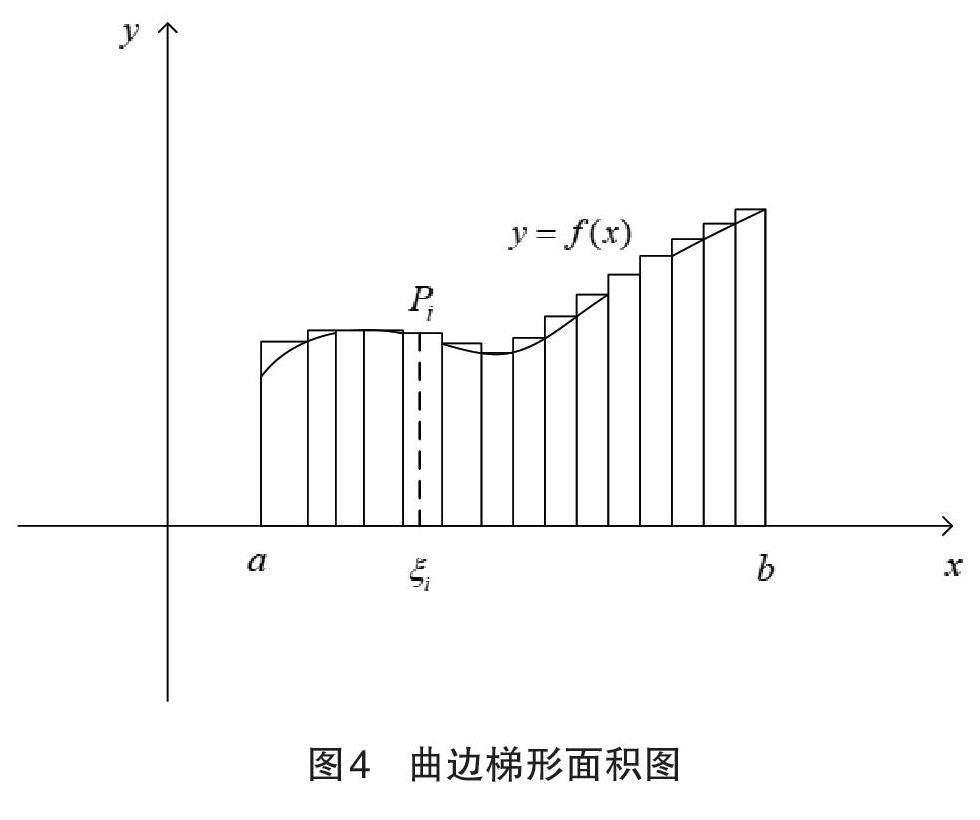
一元函数定积分的几何意义是求曲边梯形的面積，采用“分割取近似，求和取极限”的思想，具体如图4 所示。高等数学中介绍定积分的求解方法一般使用牛顿—莱布尼茨公式，很少利用定义求解，是因为利用定义求解过程繁琐且容易出错，但对有些函数来说，很难找到其原函数，因此，需要借助定积分的定义求其数值解。虽然可以直接调用MATLAB 的integral 函数求定积分，但大部分学生对利用定义求解定积分的过程并未理解，对integral 函数求定积分的内部实现机制并不明白。尤其对计算机类专业学生来说，如何用定义实现定积分的求解过程比较重要：一方面可以深入理解定积分的定义及几何意义；另一方面实现学科的交叉融合及为后续课程学习夯实基础。

运行结果得如图5 所示，所围成阴影图形的面积即为定积分的结果。

解1：利用integral 函数求解定积分。

在MATLAB 中编写代码如下：

fun=@（x）x.^2

ans=integral（fun，0，1）

运行结果ans=0.3333。

解2：利用定积分定义自行编写代码。

%在0-1 区间内产生n=100 个随机点

x=rand（1，100）；

x=sort（x）；

x=［0 x 1］；

sum=0；

for i=1：length（x）-1

delta_x=x（i+1）-x（i）；

sum=sum+（x（i）+delta_x/2）.^2*（x（i+1）-x（i））；

end

运行结果与上述方法一致。

2.2 二元函数定积分

二元函数定积分简称二重积分，其几何意义即是求曲顶柱体的体积，实施过程与一元函数定积分类似，均是“分割取近似，求和取极限”。下面以二重积分在直解坐标系下的计算为例加以阐释，如图6 所示。很多学生空间想象力较弱，不能准确绘制题目所给的区域，导致无法顺利求解，但如果能借助MATLAB 软件作图，则能直观展示空间图形从而使问题迎刃而解。

例3 求由4 个平面x = 0x = 1y = 0y = 1 所围的柱体被平面z = 0及2x + 3y + z = 6截得的立体的体积。

在MATLAB 中编写如下代码：

［x，y］=meshgrid（0：0.01：1）；

z=6-2*x-3*y；

meshz（x，y，z）；%将曲面加上围裙

xlabel（'x'）；

ylabel（'y'）；

zlabel（'z'）；

运行结果得如图7 所示。

可见，在MATLAB 软件中也可轻而易举地实现立体图形的绘制，增强了学生的空间想象力。由于二重积分在计算过程是分两次一重积分来实现的，但在计算过程中会碰到与一重积分同样的问题，即原函数难以求解，故可调用MATLAB 软件自带quad2d 函数或二重积分的定义自行编写代码求解，这样既理解了定积分定义的过程又训练了交叉学科的融合。

解1：利用MATLAB 自带函数求解代码。

fun=@（x，y）6-2*x-3*y；

x_min=0；

x_max=1；

y_min=0；

y_max=1；

result=quad2d（fun，x_min，x_max，y_min，y_max）

运行结果ans=3.5000

解2：利用二重定积分定义自行编写代码。

x=0：0.01：1；

y=0：0.01：1；

sum=0；

for i=1：length（x）-1

delt_x=x（i+1）-x（i）；

dx=x（i）+delt_x/2；

for j=1：length（y）-1

delt_y=y（i+1）-y（i）；

dy=y（j）+delt_y/2；

sum=sum+delt_x*delt_y*（6-2*dx-3*dy）；

end

end

sum

運行结果与上述方法一致。

上述利用定义自行编写代码求解定积分的过程中，未使用求极限这一步骤，仅仅体现几何图形分割得越细，计算结果越精确，它是一种计算定积分数值解的有效方法，对理解定积分的定义及几何意义均有所帮助。因此，在授课过程中教师应使用数形结合和动手实践，让学生对所学内容掌握得更扎实。正所谓“耳听千遍，不如手过一遍”。

3 结语

本文以计算机类专业为例，从函数应用场景、一元函数定积分以及二元函数定积分这3 个方面展示了MATLAB 软件辅助高等数学教学，不再停留在传统的“黑板+粉笔”和多媒体授课方式，而是呈现知识点的具体应用场景，利用自行编写代码理解定积分的定义，从而激发学生的学习兴趣和动手能力，实现学科的交叉融合，提高教学质量和效果。