图形直观和代数表达

张娟萍

【摘要】借助图形准确把握问题特征，用代数表达揭示数量关系.本文从“有理数”复习出发，以数和形的两个方面贯穿“有理数、平方根、整式乘法，坐标系、多维空间、向量”等中学数学学习的整个过程，由一维到二维到多维，整合点线面体的思想，由数与字母、图形与代数联通，体现数学学习对学生而言是已有知识不断扩张、按一个逻辑方式生长出来的.数学知识探究过程就是学生思维的拓展和创造的过程.

【关键词】图形直观；代数表达；有理数

1 引言

从浙教版七年级上“有理数”复习出发，以数和形两个方面贯通知识的发生和发展脉络，贯穿中学数学学习的整个过程，由有理数的概念、有理数的运算、实数和代数式，进一步作思维和方法的拓展到直角坐标系、空间直角坐标系以及向量等.

2 数的表达与图形表现

问题1 有理数表达方式区别于小学常用的自然数表达，有什么特征？

生 与小学的数比较，表达一个有理数有两部分——符号和数值.

问题2 那么还有什么办法表示数呢？不同的表示方法怎么统一呢？

学生发现，数轴上的点可以表示数.数的表示中符号对应数轴上原点左右的方向，数的表示中数值部分对应数轴上点的位置距离数轴原点的长度，这样就建立了有理数与数轴上点的对应关系.

我们把数的概念和计算联系到图形的表示为：符号对应方向，数值对应线段长度.

3 有理数相关概念的图形表现

问题3 有理数这一章提到了很多相关概念，能否用这两种方法统一表示呢？

学生先独立思考，再群组互动：有理数学习的相关内容包括有理数定义、相反数、绝对值、有理数比较大小、有理数的加减乘除运算，进一步到乘方、开方运算. 学生互动交流，并将所有的结论分类和细化，达成共识.

4 有理数运算的图形表现

4.1 有理数加法的图形表现

学生用数轴表示两个有理数相加时，以一个加数在数轴上的点为起点，加另一个加数，如果是负的，就向左方向移动该加数数值所对应的单位长度，到数轴上所在点的位置，得到结果；如果另一个加数是正的，就向右方向移动对应的单位长度，同样得到结果.所以，加减运算（减法转化为加法）其实就是数轴上的线性运算.

学生们研究得到加法运算的图形表现，相当于由一个点（被加数）所在位置出发，向左或右（加数的正或负）移动一段距离（加数的数值），得到的和就是所在点的位置.

4.2 有理数乘法的图形表现

有理数乘法运算，怎么样用图形的方式来体现呢？

生 两数相乘时想到的图形就是长方形面积.

那么长方形如何在数轴上体现出来呢？

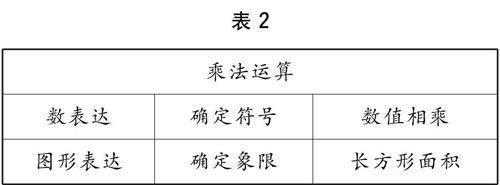
学生交流 乘法得到图形的面积相当于加法得到数轴上的长度，乘法得到的符号该如何体现呢？类比数轴的方向表示符号的办法，在这个直角坐标系中也得规定图形所在区域的符号，这就是直角坐标系的象限符号，如表1.

例如 -3×（-2）在直角坐标系中表示：在横轴上取-3；在纵轴上取-2，得到第三象限中面积为6的长方形，第三象限取正，所以-3×（-2）的结果表示为+6，如表2.

4.3 有理数平方、开方的图象表现

师 平方运算怎么在坐标系中用图形体现呢？如，22，（-2）2；用直角坐标系以图形表现？

生 平方运算，两个数一样，即符号和数值一样的，图形在一、三象限内的正方形.

反过来，说明开方运算，正方形其边长是相同的两个值，对应的数分别在横轴与纵轴的正负半轴上，说明了一个正数开方后有正负两个平方根.

4.4 有理数乘方的图形表现

师 有了前面的启示（乘法转化成图形面积表示），大家能否用图形表示立方呢？如，你能用图形表示（2.7）3吗？

生 用立方体，如何放到数轴上呢？

生 可以用三条数轴.用空间模型展示（三维坐标）.

为了研究空间图形与数的关系，需要建立空间的点与有序数组之间的联系，为此我们通过引进空间直角坐标系来实现.过定点O，作三条互相垂直的数轴，都以O为原点且具有相同的长度单位.这三条轴分别叫做x轴（横轴）、y轴（纵轴）、z轴（竖轴），统称坐标轴.通常把x轴和y轴配置在水平面上，而z轴则是铅垂线，三条坐标轴组成了一个空间直角坐标系，点O叫做坐标原点.

由学生在三维坐标中表示-3×（-2）×2，并归纳一般方法.

4.5 有理数数形结合的思维拓展

师 有些同学肯定还会想4次幂、5次幂、更多次幂怎么办？

生 可以建立多维空间坐标系.

生 三个有理数相乘，想到立方体的体积，要建立三维坐标系.同样的思维，多个有理数相乘，可以抽象到多维的坐标系表示.

师 在解决问題的过程中，可以大胆拓展和创设，由点想到线想到面想到体，然后创设数轴—直角坐标系—空间直角坐标系—多维直角坐标系，可以说思路打开，创造力无限.你们还有什么新奇的想法？

生 圆弧形数轴，圆形时钟的圆周有均匀刻度可以规定正方向、单位长度、原点，可以类比数轴.

5 整式乘法的图形表现

5.1 图形几何意义

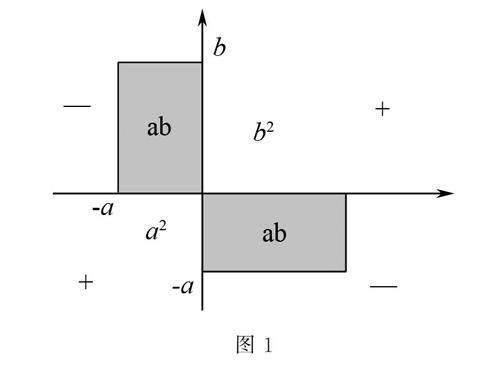
下面选择浙教版七年级下第六章多项式的乘法运算的典型例子——两数差的完全平方公式（b-a）2=b2-2ab＋a2，用图形来解释等式的意义.

生 等式右边表示边长为（b-a）的正方形面积，等式左边表示总的面积为：边长为b的正方形面积＋边长为a的正方形面积-2个长为a宽为b的长方形面积的总和.根据图形整体等于局部之和，所以等式成立.

5.2 整式乘法的图象表现

数的乘法可以在直角坐标系中的图形面积及象限符号表现，同样的方式可以在直角坐标系内表示式（字母表示数）的乘法，如上例两数差的完全平方公式.

生 如图1中，（b-a）2在直角坐标系所表示图形为：边长为（b-a）的正方形，一边（b-a）放在横轴上，b是正的，取原点右侧b的长度单位，-a是负的，取原点左侧a的长度单位；另一边（b-a）放在纵轴上，b是正的，取原点上侧b的长度单位，-a是负的，取原点下侧a的长度单位.b2-2ab＋a2在直角坐标系所表示图形为：边长为b的正方形面积是b2的数值，由于在第一象限；边长为a，b长方形的面积是ab的数值，由于这两个长方形分别在二、四象限，所以符号取负，因此得到-2ab，边长为a的正方形面积是a2的数值，由于在第三象限，所以符号取正.两者说的是同一个图，所以它们的值完全相同.

5.3 整式表达和图象直观的向量解释

在初中数学教材中，学习整式乘法的时候要求表示它的几何意义，就是用整体面积等于局部面积之和来验证乘法公式成立，代数表达仅体现在数值的角度.而在直角坐标系内表示整式乘法，是体现代数表达的时候数值与符号全体参与的过程.

如何找到二者恰当的解释呢？下面从向量[5]的角度作一些分析.向量是既有大小又有方向的量，它与数值和符号相对应，数与式的加法运算相当于平行向量（也叫做共线向量，是指方向相同或相反的非零向量）的和差，加法运算，相当于线性运算.数与式的乘法运算相当于平行向量乘数运算，实数λ与向量a的积是一个向量，这种运算叫做向量的乘数，记作λa.当λ>0时，λa的方向和a的方向相同，当λ<0时，λa的方向和a的方向相反，当λ = 0时，λa=0，这样就实现了代数与几何的融合.

6 结语

本课的明线是数形结合，把代数表达与图形的直观表现，联系起来，由有理数复习出发，引导学生串起所有学过的知识，由一维的数轴拓展到二维直角坐标系、三维空间直角坐标系.用几何图形来解构有理数、整式乘法，沿途所产生的所有知识（包括平方根、坐标系、乘法公式、多维空间）对学生而言不是完全新的东西，而是已有的东西的不断扩张，它整合了点线面体的思维、整合了数与字母的自然转换，冲破了教材编排的顺序和结构，让知识按同一个思想连贯起来.找到一个合适的逻辑，初一的有理数和乘法公式、初二和高中的直角坐标系，甚至大学的多维空间，都是由已有知识扩展起来.本课暗线是学生思维的拓展和创造，体现数学学习的一般方法.

参考文献：

[1]义务教育数学课程标（2022年版）[M].北京：北京師范大学出版社，2022.5.

[2]义务教育教科书.数学 七年级上册[M].杭州：浙江教育出版社，2012.

[3]义务教育教科书.数学 八年级上册[M].杭州：浙江教育出版社，2012.

[4]义务教育教科书.数学 七年级下册[M].杭州：浙江教育出版社，2012.

[5]普通高中教科书.高中数学（必修2）[M].北京：人民教育出版社，2017.