一道双中点几何题的多角度解答

高亮荣

【摘要】添加辅助线是解答几何题的一个基本策略，要求对题目的重要条件作分析，对基本图形进行理解与联系，运用图形之间的关联探索思考问题.下面以一道双中点问题作解题分析．

【关键词】初中数学；辅助线；解题技巧

例题 如图1，已知在△ABC中，AB=AC，CE是AB边上的中线，延长AB至点D，使BD=AB．求证：CD＝2CE．

解析1 因为CE是中线，如图2.

延长CE至点F，使EF=EC，这样出现CF＝2CE，只要证明CF＝CD即可，连接BF，联系已知条件，图形中有全等三角形.

易得△EAC≌△EBF（SAS）．

则BF=AC=AB =BD，∠EBF=∠A．

又∠ABC=∠ACB，

所以∠FBC=∠FBE+∠EBC=∠A+∠ACB=∠DBC，

所以△FBC≌△DBC（SAS），

即CD=CF=2CE．

点评 上述辅助线是典型的“中线倍长”法．由中点的条件，将中线延长一倍，证明△EAC≌△EBF，并利用全等的结论，证明△FBC≌△DBC.

同样的方法，延长CE到点F，使得EF= CE，连接AF，证明△AEF≌BEC，△CAF≌△DBC．

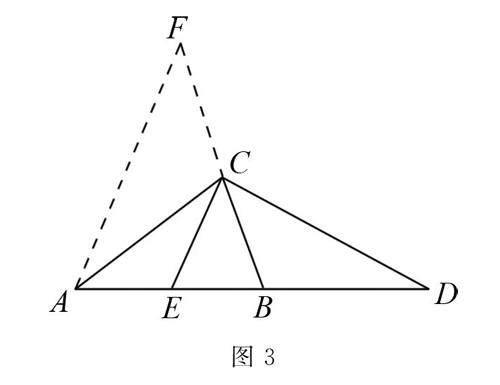
解析2 因为CE是中线，则点E是AB的中点，如图3.

可以在BC的延长线上截取CF=CB，构成三角形的中位线，得到AF＝2CE，只需求证AF＝CD.

AF与CD分别在△FCA和△CBD中，

易得FC=CB，AC=AB =DB，

由邻补角得∠FCA =180°-∠ACB，

∠CBD=180°-∠ABC，

又AB=AC，则∠ACB=∠ABC．

所以△FCA≌△BCD（SAS）．

点评 上述的辅助线立足于“点E是AB的中点”，延长三角形的另一边，构成三角形的中位线，并证明△FCA≌△BCD.

同样的方法，如图4.

延长AC至点F，使CF=AC．连接BF，DF．

所以AF=2AC=2AB=AD．

因为AC=AB，∠A=∠A，AD=AF，

所以△ABF≌△ACD（SAS）．

所以BF=CD．

因为CE是△ABF的中位线．

所以CE=1/2BF=1/2CD．

所以CD=2CE．

结语

对一个陌生问题，认真审题是解题的基础，可以由已知向结论推理，或由结论向已知推证；或者从两边向中间追寻，寻找已知与结论之间的桥梁．由题目的已知条件能够挖掘出什么重要结论？由条件能联想到什么？由结果还能联想到什么？如本题重要的条件只有两个：（1）等长线段AB=AC；（2）在同条线段上的两个中点.从不同角度去思考，会产生不同的思考途径，所用的基础知识和方法也就不同，如解析一是基于“E是AB边中点”，采取“中线倍长”法，证明两个三角形全等进行解答，方法经典且适用.解析2，利用“E是AB中點”，将三角形的另一边倍长，使CE为新三角形的中位线.解析3，利用“点B为AD中点”的条件，通过作三角形另一边中点，构成三角形的中位线.后面几种辅助线的视角独特，运用中点的条件构造三角形中位线，独辟蹊径，体现了创新思维的运用，也培养了学生理性思考的能力.