等腰三角形考点直通车

凌泉

【摘要】等腰三角形是初中数学中的一个重要知识点，它的有关知识在平面几何的计算和证明方面有非常广泛的应用．近几年的中考考题中，有关等腰三角形的考题出现得较多，考法也比较新颖．本文先对有关等腰三角形的考点进行概述，然后以例题的形式阐述等腰三角形考点的几种常见考法，供学生复习备考时参考．

【关键词】初中数学；等腰三角形；解题

1 等腰三角形重要考点概述

等腰三角形是初中数学中的一个重要知识点，现将涉及等腰三角形的中考考点加以阐述．第一，与等腰三角形性质有关的考点，主要有：等边对等角（即等腰三角形的两个底角相等）和三线合一（即等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合）；第二，与等腰三角形判定有关的考点，主要有：“有两边相等的三角形是等腰三角形”和“有两个角相等的三角形是等腰三角形（等角对等边）”.

2 等腰三角形重要考点例析

2.1 根据等边对等角求角度

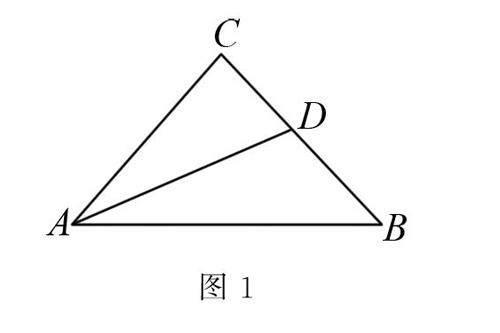
例1 如图1所示，AD是△ABC的角平分線，AC=BC，∠ADC=60°，求∠C的度数．

解析 令∠BAD=x，

因为AD平分∠BAC，

所以∠CAD=∠BAD=x，∠BAC=2x（角平分线的定义），

因为AC=BC，

所以∠B=∠BAC=2x（等边对等角），

又因为∠ADC=∠B+∠BAD（三角形外角的性质），

所以2x+x=60°，得x=20°，

所以∠B=∠BAC=40°，

在△ABC中，

因为∠BAC+∠B+∠C=180°，

所以∠C=100°．

点评 本题考查了等腰三角形的性质和角平分线的定义，根据等边对等角求角度，学生熟练掌握各知识点是解题的关键．

2.2 根据等角对等边求边长

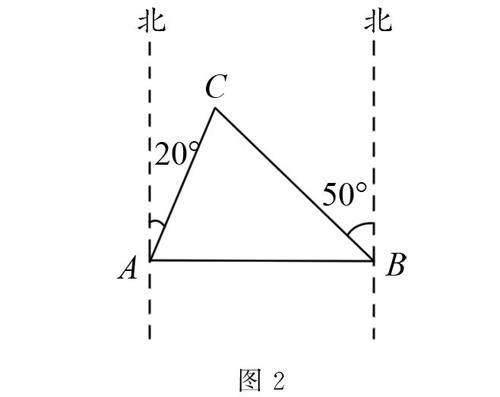
例2 如图2所示，灯塔B在灯塔A的正东方向，且AB=75km．灯塔C在灯塔A的北偏东20°方向，灯塔C在灯塔B的北偏西50°方向．

（1）求∠ACB的度数；

（2）一轮船从B地出发向北偏西50°方向匀速行驶，5h后到达C地，求轮船的速度．

解析（1）根据题意得∠BAC=70°，

∠ABC=40°，

所以∠ACB=180°-∠BAC-∠ABC=

180°-70°-40°=70°.

（2）因为∠BAC=∠ACB=70°，

所以BC=AB=75km，

所以轮船的速度为v=BC/t=15km/h．

点评 本题考查方位角、等腰三角形的判定、三角形的内角和定理，学生熟练掌握等腰三角形的等角对等边是解答本题的关键．

2.3 根据“三线合一”求解有关实际问题

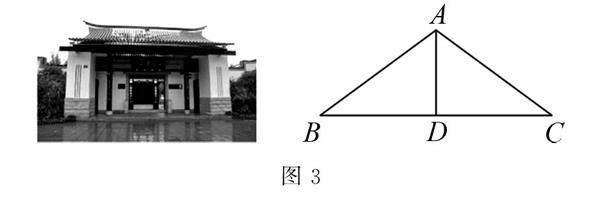
例3 筼筜书院是厦门第一座现代书院，位于国家重点公园——白鹭洲公园东区．筼筜是竹之雅称，书院以竹命名，自此鹭岛贫筜湖畔于竹林环水，桃李缤纷之中，多了一处可供商量旧学，培养新知之地．如图3所示，“筼筜书院”的顶端可看作等腰三角形ABC，AB=AC，D是边BC上的一点．下列条件不能说明AD是△ABC的角平分线的是（）

（A）BD=CD.（B）∠ADB=∠ADC.

（C）S△ABD=S△ACD.（D）BC=2AD.

解析 因为△ABC是等腰三角形，AB=AC，

所以BD=CD，

所以AD是△ABC的角平分线，

故（A）选项不符合题意；

因为∠ADB+∠ADC=180°，

所以∠ADB=∠ADC=90°，

即AD是△ABC的高线，

因为△ABC是等腰三角形，AB=AC，

所以AD是△ABC的角平分线，

故（B）选项不符合题意；

因为S△ABD=S△ACD，

所以BD=CD，

所以AD是△ABC的角平分线，

故（C）选项不符合题意；

若BC=2AD，不能说明AD是△ABC的角平分线，故（D）选项符合题意.

点评 此题考查了等腰三角形的性质，学生重点掌握等腰三角形“三线合一”的性质是解答本题的关键．

2.4 根据“三线合一”证明

例4 如图4所示，在△ABC中，AB=AC，点D，E分别为边AB，AC上的点，DE∥BC，将△ABC沿DE对折，点A落在点A＇．

（1）请你根据图形，利用无刻度的直尺作出边BC的垂直平分线；

（2）请你运用所学的知识，证明所作的直线为边BC的垂直平分线．

解析 （1）如图5所示，直线AA＇即为BC的垂直平分线.

（2）由翻折可得AA＇⊥DE，

因为DE∥BC，

所以AA＇⊥BC，

因为AB=AC，

所以△ABC为等腰三角形，

所以直线AA＇即为BC的垂直平分线．

点评 本题考查了作图、基本作图、根据“三线合一”证明有关问题．

3 结语

等腰三角形是初中数学中的一个重要考点，掌握等腰三角形的性质和判定方法，能够助力学生更好地解决相关的数学问题．同时，等腰三角形在实际生活中也有很广泛的应用，例如在建筑设计、工程测量、物理学等领域都有广泛的应用，应当引起学生的足够重视．

参考文献：

[1]王成栋.巧用等腰三角形的“三线合一”性质解题[J].现代中学生（初中版），2023（20）：33-34.

[2]鲍聪晓.等腰三角形重要题型解析[J].中学生数理化（八年级数学）（配合人教社教材），2023（10）：6-8.

[3]安娜.等腰三角形常见解题误区[J].初中生世界，2023（15）：57.

[4]蔡建华.刍议等腰三角形问题中的分类讨论[J].初中数学教与学，2023（07）：25-27.

[5]周贵胜.巧用等腰三角形旋转解题[J].初中生学习指导，2022（33）：22-24.