巧用数学思维解初中物理题

张丽娟

【摘要】在中学物理学习过程中，特别是涉及较为复杂的问题时，往往会陷入困境.这主要是由于学生没有把握问题的实质，因此要引导他们学会多种解题方法，尤其是要学会利用数学的概念来解决物理问题，注意训练学生的思考能力，全面训练他们的思维，使学生解决问题的能力得到提升.本文对初中物理教学中应用的几种思想进行归纳和总结，以期对初中学生解决问题起到一定的指导作用.

【关键词】数学思维；初中物理；解题技巧

将数学原理运用于中学物理教学中是一项具有挑战性的任务.然而，运用数学思想解决物理问题在初中阶段还比较少见，在高中的课本、习题、竞赛试题等方面，却处处可见运用数学思想的痕迹.这就要求在对物理概念、图像和模型有清晰的认识的基础上，选取合适的研究对象，对物理问题进行分析和解决[1].如果学生掌握数学思想的思维方法，就会更主动，眼界也会更宽，对自己所学的知识也会有更深刻的了解，在求解问题时，可以启发自己的解题思路，从而发现一种十分简洁而又高效的解决问题的方法.

1 比例思维

所谓“比例思维”，就是将相同的物理变量在各种条件下，通过比率对某些物理参数进行约化，减少中间的联系，凸显主要因素，使得计算过程变得简单快捷[2].

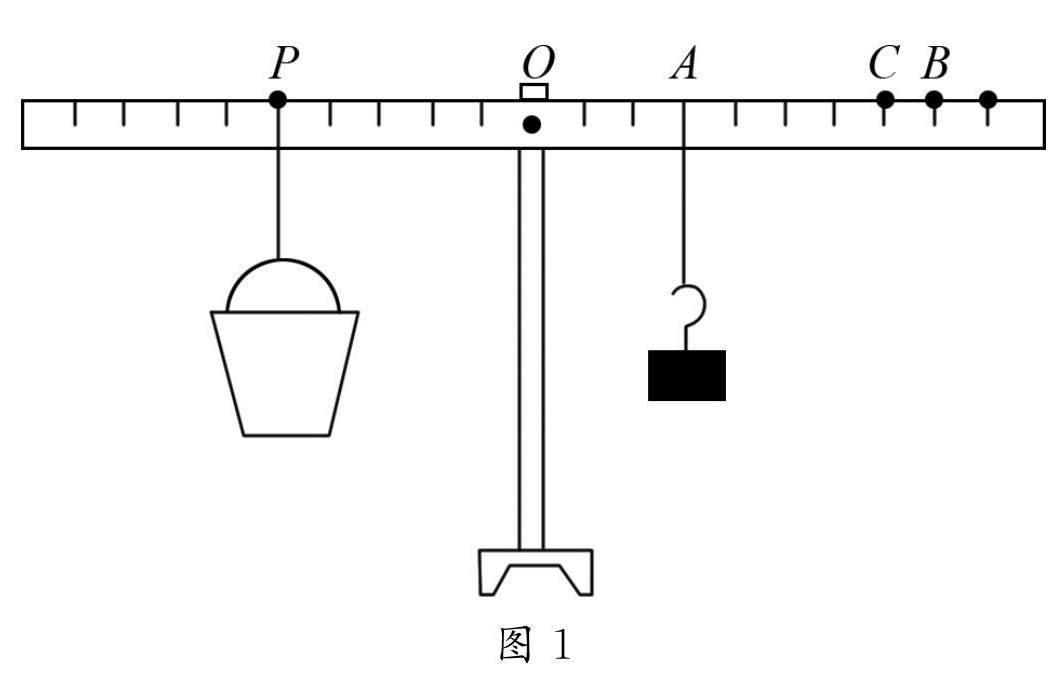
例1 小文在使用一把平衡尺（标明等距刻度的起始位置为等长的横档）.从图1中可以看出，先将一个空的水桶吊在刻度线P上，将重量50克的挂钩吊在刻度线A上，使操纵杆处于水平状态.在不更换吊瓶的情况下，将吊瓶装入半桶水，将吊瓶吊到刻度线B，控制杆处于水平状态，使其处于平衡状态.将桶中的水全部倒出，再往里面倒半桶水，然后将桶悬在刻度线P处，将钩子悬在刻度线C处，这样就可以使操纵杆始终处于水平状态.由此可测得该种液体的密度是kg/m3.

分析与解 想要得到流体的浓度，必须掌握流体和水的容积相等，运用杠杆定律，通过推导出相应的等式来解决.

设空桶的重力为G1，水的重力为G2，液体的重力G3，钩码的重力为G4，由F1×L1= F2×L2，则G1+G2×OPG1×OP=G4×OBG4×OA  G2G1=OAOB－OA ①，G1+G3×OPG1×OP=G4×OCG4×OA  G3G1=OAOC－OA ②，由①②得，G3G2=OC－OAOB－OA=45，又G=mg=ρVg，且V相同，故ρ液ρ水=G3G2=45，即ρ液=45ρ水=45×1.0×203kg/m3=0.8×103kg/m3.

2 极限思维

所谓的“极限思维”就是依据相关的物理法则，在一定的范围内，把其所包含的变量进行适当的扩展，将这些变量的数值（通常是指其极限值）进行对比，作出相应的判定[3].

例2 家用线路的导线都带有一些阻抗（大约为数欧），所以当家中使用高功率的家电，如空调或电炉时，家中原本亮着的灯泡将会变成黑色.在“创造素养实践行”的过程中，一位学生经过试验，能够估计出家中电路导线部分的电阻，如图2所示，将家用线路导线部分的总电阻设为r，L是一个普通的家用白炽灯泡，M是一台空调器.在试验过程中，首先将开关S打开，然后再将灯泡L打开，测量出在灯泡上的电压为U1，而灯泡的功率为P1；再次关闭开关S，测量出在电灯泡上的电压是U2，而空调器的电力是P2（P2＞P1）.试写出估算r的表达式（只用U1、U2和P1表示设电源电压恒定）.

分析与解 当S被切断时，电灯泡和输电线成了一个串联，因为电灯泡的电阻比输电线的阻值大得多，所以输电线的电压分压效应可以不考虑，也就是U电源=U1.如果将开关S关闭，则将空气调节器与电灯泡并联，然后再与输电线串联，因为空气调节器的电力比电灯泡的电力要大得多，所以在粗算时，电灯泡的能量可以不计，但是要把电力线的电阻和电压分压的影响加以考虑.即Ur=U1-U2，Ir=I空调，又P=UI，I=UR，则r=U1－U2P2U2=U1－U2·U2P2.

3 方程思维

所谓的“方程思维”就是通过构造一个包含待知变量的方程（或不等式），呈现其与已知变量之间的等价（或不等量）关系，从而解决待测变量[4].在物理学的求解中，要将问题所告知的已经知道的数量，运用物理法则来构建等式（或方程组），能让问题变得简单明了.

例3 正如在图3（甲）中所示，木位于小块B的上面木块刚好浸入到水里.把金属块放在水里，容器底对金属块A的支撑力为2N；当木块不动的时候，只有25的体积露出水面，见图3（2）.可知木块的体积是金属块的5倍，求出金属密度和木块的重力（g=10N/kg）.

分析与解 根据受力平衡分析，可列出三个等式方程.

F1=GA+GB

ρ水gVB=ρAVAg+ρbVBg ①，

FB=GB

ρ水g1－25VB=ρBVBg ②，

FA+F支=GA

ρ水gVA+F支=ρAVg ③，

由②得ρB=0.6×103kg/m3 ④，

又VB=5VA ⑤，

将④⑤代入①得ρA=2×103kg/m3，

将ρA代入③得

GA=2×10-4kg/m3×5×2×10-4m3×10N/kg=6N.

4 結语

从上面的例题可以看出，如果能灵活地使用数学思维将有关的物理定律和方程式合理地组合起来，并且从多个方面来思考解决问题的方法，能够使学生们的物理思想更加灵活.但是任何一种思维方式都存在着一定的限制，如果在课堂上做大量的习题，而忽视对学生思考能力的培养与提升，那么就会适得其反.在日常的物理教学与比赛指导中，要注重对学生解决问题的思考能力的培养与提升.

参考文献：

[1]丁海生.初中物理教学中拓展数理融合路径的实践举隅[J].广西物理，2023，44（03）：137-139.

[2]尤长江.探寻初中物理学习中正确的解题思路[J].科教文汇（中旬刊），2020（05）：139-140.

[3]黄宏鹏.浅谈应用数学处理物理问题能力的培养[J].河南科技，2015（23）：264.

[4]朱坤燕.浅析数学方法在物理教学中的应用体现[J].才智，2015（36）：59.