用生成函数求几类数列的通项公式

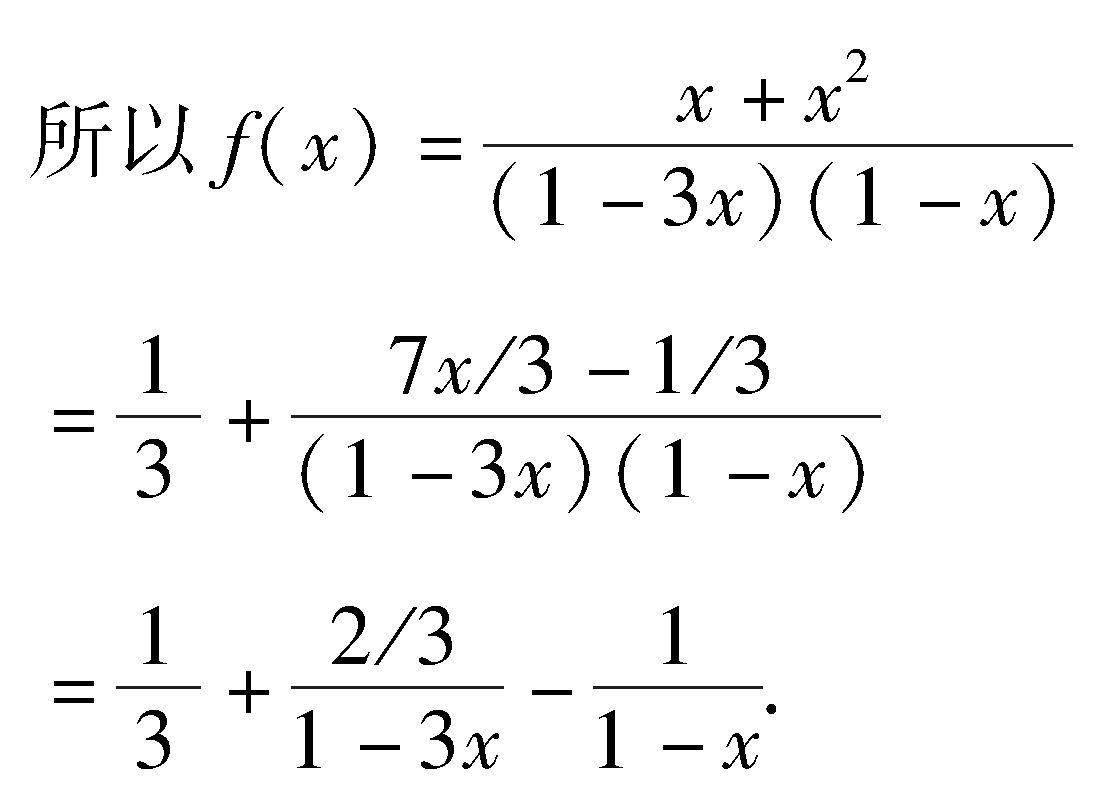
摘 要：高中数学数列通项公式不仅是高考考查的重点和热点，还是高等数学的重要基础.利用高中数学数列通项公式的求解技巧，可以有效培养学生的数学思想和数学学科素养.文章介绍了生成函数，并利用生成函数来求解几类有难度的数列的通项公式.

关键词：生成函数；形式幂级数；数列；通项公式

中图分类号：G632   文献标识码：A   文章编号：1008-0333（2024）07-0024-05

生成函数是组合数学中的一个重要概念，通过生成函数可以把离散数学和连续数学巧妙地连接起来.利用生成函数来处理中学数学中的数列通项问题，问题的可操作性强，学生容易理解.

1  预备知识

定义1[1] 设a0，a1，…，an，…是一个给定的数列，我们称形式幂级数

a0+a1x+…+anxn+…为这个数列的生成函数.

例如，数列1，2，3，…，n，…的母函数是1+2x+3x2+…+nxn+….

注 为了应用形式幂级数去解决数列通项公式问题，我们引进形式幂级数之间的加法、减法、乘法等运算，并规定：在进行这些运算时，把形式幂级数看成幂级数，然后按幂级数的运算法则去进行运算.

所以定理1得证.

由定理1，有

2 利用生成函数求数列通项公式的步骤

（2）根据数列的递推关系求出f（x）；

（3）把f（x）展开成形式幂级数；

（4）求出xn的系数.

由此可见，利用生成函数来理解数列通项后，求解数列通项就不再是玩技巧了，而是程序性的操作.

3 常系数线性齐次递推数列

例1 设数列an满足an-10an-1+21an-2=0，且a1=3，a2=93，求通项公式an.

解析 因为an+2-10an+1+21an=0，且a1=3，a2=93，设数列an的生成函数为

f（x）=a1x+a2x2+a3x3+…+anxn+….

上式两边乘以（-10x），得

-10xf（x）=-10a1x2-10a2x3-…-10an-1xn-…，

上式两边乘以21x2，得

21x2f（x）=21a1x3+…+21an-2xn+….

三式相加，得

（1-10x+21x2）f（x）

=a1x+（a2-10a1）x2+（a3-10a2+21a3）x3+…+（an-10an-1+21an-2）xn+…

=a1x+（a2-10a1）x2

=3x+63x2，

用待定系数法，有

故an=3×7n-6×3n.

例2[3] （2020年福建省数学竞赛试题）已知数列an满足a1=1，a2=5，an+2=4an+1-3an（n∈N*）.

（1）求数列an的通项公式；

f（x）=a1x+a2x2+a3x3+…+anxn+an+1xn+1+an+2xn+2+…，

-4xf（x）=-4a1x2-4a2x3-…-4an+1xn+2-…，

3x2f（x）=3a1x3+…+3anxn+2+…，

将以上三式相加，并利用a1=1，a2=5，an+2=4an+1-3an（n∈N*），得

（1-4x+3x2）f（x）=x+x2.

故an=2×3n-1-1.

（2）由（1）知

A（x）=a1x+a2x2+…+anxn+…，

2xA（x）=2a1x2+…+2an-1xn+…，

-4xB（x）=-4b1x2-…-4bn-1xn-….

三式相加，得

（1+2x）A（x）-4xB（x）=-10x.①

又B（x）=b1x+b2x2+…+bnxn+…，

5xA（x）=5a1x2+…+5an-1xn+…，

-7xB（x）=-7b1x2-…-7bn-1xn-….

三式相加，得

5xA（x）+（1-7x）B（x）=-13x.②

由①和②，解得

展開成形式幂级数，得到

所以an=2n-4·3n.

所以bn=2n-5·3n.

4 常系数线性非齐次递推数列

例4[4] 已知数列an满足an-2an-1+an-2=2n，且a0=a1=1，求通项公式an.

解析 设数列an的生成函数为

f（x）=a0+a1x+a2x2+…+anxn+…，

-2xf（x）=-2a0x-2a1x2-…-2an-1xn-…，

x2f（x）=a0x2+…+an-2xn+…，

四式相加，得

f（x）=a1x+a2x2+…+anxn+…，

-xf（x）=-a1x2-…-an-1xn-…，

三式相加，得

展开成形式幂级数，得

5 一个特殊的数列

例6[5] （卡特兰数）设有一凸n边形，用n-3条在内部不相交的对角线把这凸n边形分成n-2个三角形，那么一共有多少种不同的分法？

解析 设an表示将一个凸n+1边形划分为三角形的分法数，并规定a1=1.

当n=2时，凸n+1边形是三角形，它只有一种分法，所以a2=1.

当n=3时，凸n+1边形是四角形，它只有两种分法，所以a3=2.

现设n≥3，我们在凸n+1边形T中先任意取定一条边，例如图1中的AB，另取一点C.设△ABC左边的图形T1是一个凸k+1边形，那么，△ABC右边的图形T2必是一个凸n-k+1边形.

根据假设，凸k+1边形T1有ak种不同的分法，凸n-k+1边形T2有an-k种不同的分法. T1，T2的每一种分法就给出整个n+1边形T的一种分法.

因为T1有ak种分法，T2有an-k种分法，故T有akan-k种分法，这种分法是对固定的点C而言的.

an=a1an-1+a2an-2+…+an-1a1.

f（x）=a1x+a2x2+a3x3+…+anxn+….

那么

根据初始值a1=a2=1和an的递推关系，得到

f 2（x）=a2x2+a3x3+a4x4+…+anxn+…

=f（x）-a1x

=f（x）-x.

这就是说，f（x）满足一元二次方程f（x）2-f（x）+x=0.

因为f1（0）=1，f2（0）=0，而我们要找的f（x）满足f（0）=0，所以只能取

下面把f（x）展开成形式幂级数即可.

利用牛顿二项式定理，有

6 结束语

给定数列的递推公式，求解其通项公式，是高考与竞赛中常见的题型.对于简单的递推公式，通过构造等差数列或者等比数列即可得解.但对于复杂且难度较大的递推公式，则需要很强的技巧才能解决.但利用生成函数，则可很好地解决难度较大的递推数列的通项公式，比如常系数线性齐次递推数列和常系数线性非齐次递推数列.利用生成函数求数列的通项公式，不仅操作性强，而且学生也容易理解.可以说，生成函数是求解递推数列的通项公式的通法.

参考文献：

［1］史济怀.母函数[M].第2版.合肥：中国科学技术大学出版社，2014.

[2] 曹汝成.组合数学[M].广州：华南理工大学出版社，2000.

[3] 李鸿昌.高考題的高数探源与初等解法[M].合肥：中国科学技术大学出版社，2022.

[4] 李鸿昌，杨春波，程汉波.高中数学一点一题型（新高考版）[M].合肥：中国科学技术大学出版社，2022.

[5] 王中平.生成函数在组合数学中的若干应用[J].贵阳学院学报（自然科学版），2016，11（01）：1-7.