空间向量基底法妙解立体几何问题

雷誉

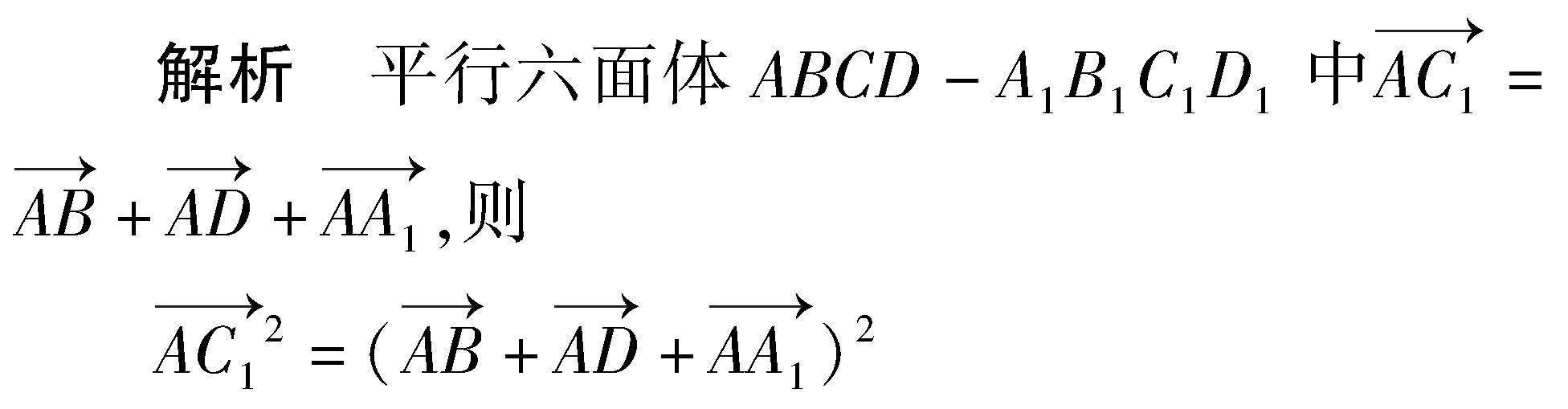
摘 要：空间向量在解决立体几何中证明位置关系和计算距离、长度、角度等问题有着广泛的应用.在解题过程中，学生习惯用坐标法来解决问题.实际中，有时受到图形的制约或是点坐标不易求出等.利用向量基底法求解是一个明智的选择，不仅过程简洁，还具有优势.其实，向量坐标法是基底法的一种特例.文章以2023年武汉二月调考中的两道立体几何问题为例，用向量基底法给大家带来一种全新的解题视角.

关键词：立体几何；基底法；向量运算；核心素养

中图分类号：G632   文献标识码：A   文章编号：1008-0333（2024）07-0020-04

利用空间向量基底法解决立体几何问题，首先要选取合适的基向量，尽量选取长度和夹角已知的向量；其次，把要解决的立体几何问题转化为向量問题，通过向量的运算解决向量问题；最后，再把向量关系翻译成几何关系，最终解决问题.

1 求距离

例1 已知四棱柱ABCD-A1B1C1D1的底面ABCD是正方形，底面边长和侧棱长均为2，∠A1AB=∠A1AD=60°，则对角线AC1的长为.

=4+4+4+2×2×2cos60°×2=20.

点评 本题以平行六面体为载体，选取有公共点A的三条棱为基向量，利用向量的运算来求AC12，本题是用基向量求距离的一种典型例题.

2 求轨迹

例2 （2023年武汉二月调考第8题）设A，B是半径为3的球体O表面上两定点，且∠AOB=60°，球体O表面上动点P满足PA=2PB，则点P的轨迹长度为（  ）.

解法1 空间中动点P满足PA=2PB的点的集合为阿氏球面（即将图1的阿氏圆C以AB为轴旋转一周得到的球面），以AB的中点E为坐标原点，AB所在的直线为x轴，过点O作AB的垂线为y

设P（x，y），由PA=2PB，得

所求的轨迹为阿氏球C与球O的交线圆，交线圆的半径r即为以O为圆心，3为半径的圆与以C为圆心，2为半径的圆的公共弦长的一半，两圆圆心距

点评 本题以阿氏圆为背景情境，过渡到阿氏球上，更加灵活，对空间想象力的要求极高.把立体几何问题转化为平面解析几何问题，即把两球相交的问题转化为两圆相交的问题，运算较为繁琐.

空间向量的基本定理：已知三个非零向量a，b，c不共面，那么对于空间任意向量p，存在唯一的实数对x，y，z满足p=xa+yb+zc.其中a，b，c为一组空间向量的基向量，叫做基底.当我们遇到某些立体几何图形本身没有很明显的垂直关系或是点坐标不易求得等问题时，不妨尝试寻找空间中三个不共面的基向量，无需建立空间直角坐标系，通过基底法解决问题.本题的具体解法如下：

整理，得c·（4b-a）=27.

所以点P到4b-a方向上的距离为

点评 利用基底法解题时，选取合适的基底十分关键，应尽可能选择三个模长已知的向量，且向量的夹角也容易得出.本题使用向量基底法更简洁快速，是一个出彩的方法，不容易想到，难点在于先利用数量积的几何意义求出投影，再把点P的轨迹的圆周长的半径转化为距离［1］.

3 证明空间的位置关系和计算空间角

（1）证明：直线A1B∥平面AD1E；

（2）若CC1⊥平面ABCD，且CC1=3，求直线BB1与平面AD1E所成角的正弦值.

解法1 （1）延长D1E和DC交于点M，连接MA交BC于点N，连接D1N，如图3.

所以CM=4=AB.

则N为BC中点.

此时A1D1∥B1C1∥BN，且A1D1=BN.

故四边形A1BND1为平行四边形.

所以A1B∥D1N.

所以A1B∥平面AD1E.

点评 第（1）问辅助线的想法是把平面AD1E延展开来，补形成四边形AD1EN，而这种辅助线的作法又是学生比较畏惧的.相比较而言，第（2）问三条直线两两垂直关系显而易见，学生毫不费力地建立空间直角坐标系，用空间向量坐标法直接计算，第（2）问本文不再赘述.

平面向量的基本定理：如果两个非零向量a，b不共线，那么向量c与a，b共面的充要条件是存在唯一的一对有序实数x，y，使c=xa+yb.如果平面外一条直线的方向向量可以用这个平面内不共线的两个向量来表示，就可以判定直线和平面平行.

所以直线A1B∥平面AD1E.

设平面AD1E的法向量为n=xa+yb+zc，则

取x=-1，则z=2，y=2.

所以n=-a+2b+2c.

4 证明比例关系

例4 （2023年圆创教育三月测评第12题）如图4，在正四面体ABCD中，棱AB的中点为M，棱CD的中点为N，过MN的平面交棱BC于点P，交棱AD于点Q，记多面体CAMPNQ的体积为V1，多面体BDMPNQ的体积为V2，则（  ）.

A.直线MQ与PN平行

C.点C与点D到平面MPNQ的距离相等

D. V1=V2

所以m=n，B正确；

CD选项本文不做说明，此外也可以将正四面体放置于正方体中研究AB选项.

5 结束语

空间向量基底法是高中数学教学中的薄弱应用，往往被人忽视，如果平时不注意使用和练习，久而久之向量的思维就会固化和钝化，以至于一说到向量法就只想到坐标法.通过以上例题的分析，利用空间向量基底法求解也是一种简洁实用的方法，希望引起大家对这种方法的注意，加深认识和体会.

参考文献：

［1］徐力.例谈基底法在立体几何解题中的应用[J].上海中学数学，2014（11）：44-46.

［2］ 魏东升.空间向量基底法在立体几何问题中的应用［J］.数理化学习（高中版），2021（05）：26-29.