一道椭圆检测题的解答、探究和推广

晏炳刚

(重庆市綦江中学,重庆 401420)

解析几何题目一直以来以命题背景丰富、呈现形式多样、理论深刻优美、解答灵活多变而深受广大师生喜欢[1].此类题目对培养学生敢于质疑、善于思考、把握本质、数形结合等能力有突出价值.为此,笔者对一道模拟题进行解法探究、背景揭秘和结论推广,供大家参考.

1 题目再现

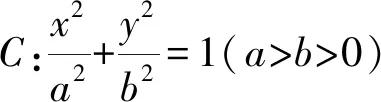
(1)求椭圆C的标准方程;

(2)设点T(2,t)(t∈R),圆T过点O且交直线x=2于M,N两点,直线AM,AN分别交C于另一点P,Q(异于顶点A).证明:直线PQ过定点,并求出该点的坐标.

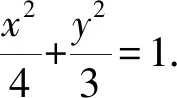
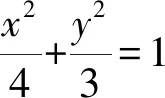
(3m2+4)y2+6mny+3n2-12=0.

易知Δ>0,设P(x1,y1),Q(x2,x2),则有

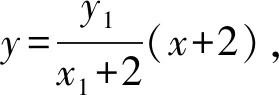
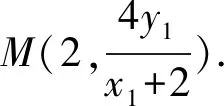
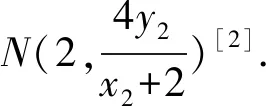
由题MN为直径的圆过点O,

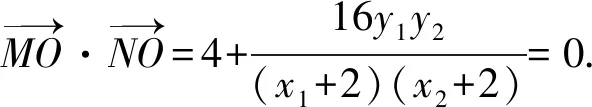
于是有

整理,得n2+n-2=0.

解得n=1或n=-2.

当n=-2时,直线PQ过点A,不合题意.

当n=1时,直线PQ为x=my+1,恒过定点(1,0).

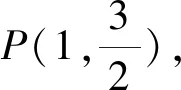
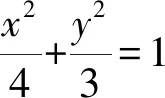
(3m2+4)y2+6my-9=0.

易知Δ>0,设P(x1,y1),Q(x2,x2),则有

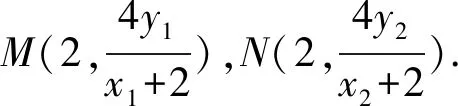
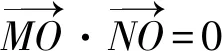
因此直线PQ恒过定点(1,0).

解法3圆T方程为

(x-2)2+(y-t)2=t2+4,

令x=2有y2-2ty-4=0.

所以yMyN=-4.

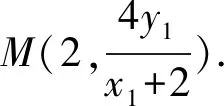
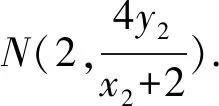
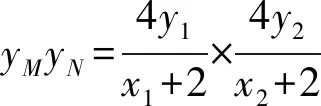
后面和解法1相同,略

评注直线过定点问题的解决方法有两种.一种设直线方程为双参数形式x=my+n,利用已知条件求解双参数关系,从而消去一个参数,再判断恒过定点.另一种为数形结合、特殊位置寻找到定点,再转化为证明任意情况过此点.

2 问题提出

新高考评价体系要求“设置新颖的试题呈现方式,促使学生主动思考、发现新问题、找到新规律、得出新结论”,基于此,做完此题,不难有以下思考:

(1)任意椭圆中,定线为x轴的过右顶点的垂线,对应定点存在吗?

(2)任意椭圆中, 定线为x轴的过任意点的垂线,对应定点存在吗?

(3)双曲线和抛物线中会有类似特征吗?

3 探究与推广

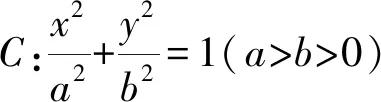
图1 命题1示意图

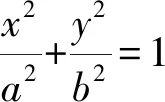
(b2m2+a2)y2+2mnb2y+b2n2-a2b2=0.

易知Δ>0,设P(x1,y1),Q(x2,y2),则有

由题知圆T就是以MN为直径过原点的圆,其方程为

(x-a)2+(y-t)2=t2+a2.

令x=a,有y2-2ty-a2=0.

所以yMyN=-a2.

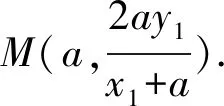
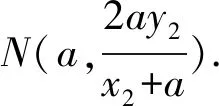
=-a2.

即m2y1y2+m(a+n)(y1+y2)+(n+a)2=0.

即(a2+4b2)n2+2a3n+a4-4a2b2=0.

即[(a2+4b2)n+a3-4ab2](n+a)=0.

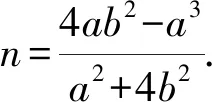
当n=-a时,PQ过点A,不合题意.

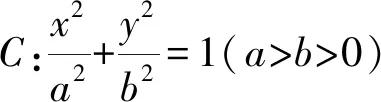
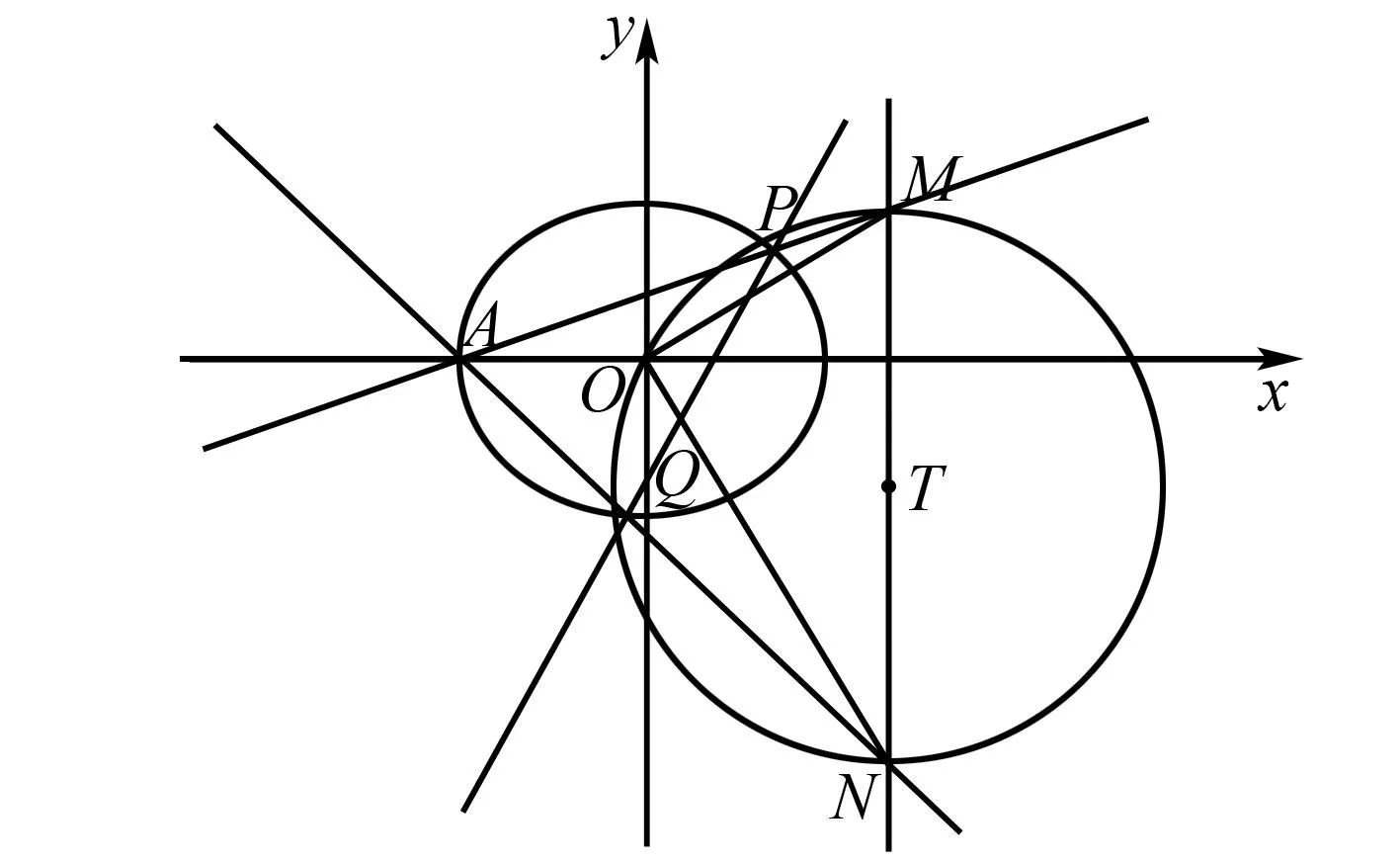
图2 命题2示意图

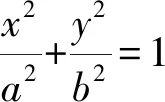
(b2m2+a2)y2+2mnb2y+b2n2-a2b2=0.

易知Δ>0,设P(x1,y1),Q(x2,x2),则有

由题知圆T就是以MN为直径过原点的圆,其方程为

(x-s)2+(y-t)2=t2+s2.

令x=s,有y2-2ty-s2=0.

所以yMyN=-s2.

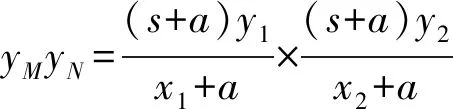
=-s2.

即[(s+a)2+s2a2)]y1y2+ms2(a+n)(y1+y2)+(n+a)2=0.

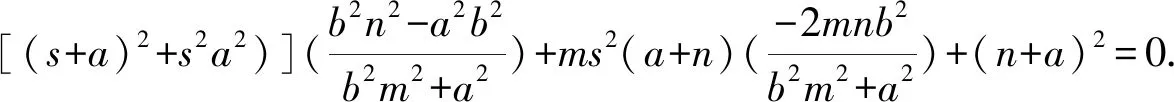
即(a2s2+b2s2+2ab2s+a2b2)n2+2a3s2n+a4s2-a2b2s2-2a3b2s-a4b2=0.

即[(a2s2+b2s2+2ab2s+a2b2)n+a3s2-ab2s2-2a2b2s-a3b2](n+a)=0.

所以n=-a或

当n=-a时,PQ过点A,不合题意.

把椭圆背景改为双曲线有以下命题.

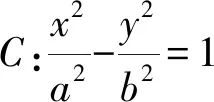
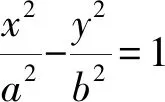
(b2m2-a2)y2+2mnb2y+b2n2-a2b2=0.

易知Δ>0,且b2m2-a2≠0,设P(x1,y1),Q(x2,x2),则

由题知圆T就是以MN为直径过原点的圆,其方程为

(x-s)2+(y-t)2=t2+s2.

令x=s,有y2-2ty-s2=0.

所以yMyN=-s2.

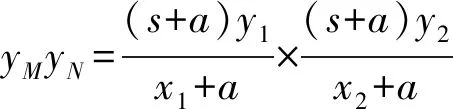
=-s2.

即[(s+a)2+s2a2)]y1y2+ms2(a+n)(y1+y2)+(n+a)2=0.

即(b2s2-a2s2+2ab2s+a2b2)n2-2a3s2n-a4s2-a2b2s2-2a3b2s-a4b2=0.

即[(b2s2-a2s2+2ab2s+a2b2)n-a3s2-ab2s2-2a2b2s-a3b2](n+a)=0.

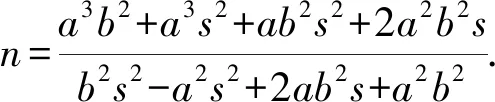
当n=-a时,PQ过点A,不合题意.

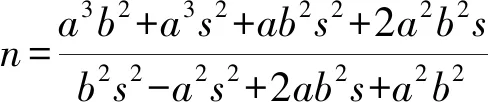
把命题3中x=s改为x=a得到一个推论即命题4.

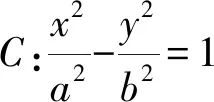
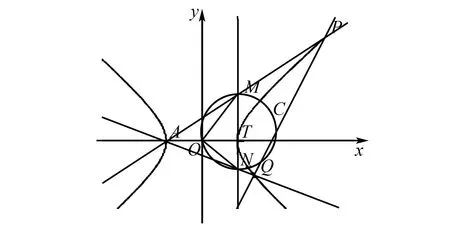
图3 命题4示意图

抛物线中以左右无穷远处为左右顶点,即过直径端点作x轴平行线,寻P,Q,见下面命题5.

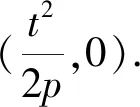
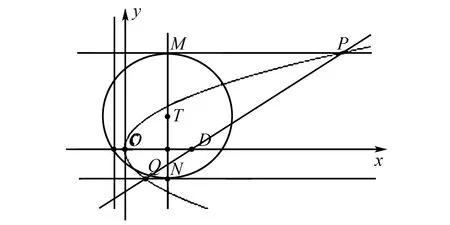
图4 命题5示意图

证明直线PQ斜率不为0,故设方程为x=my+n,与y2=2px联立有

y2-2pmy-2pn=0.

设P(x1,y1),Q(x2,x2),则有

y1+y2=2pm,y1y2=-2pn.

设T(t,h),由题圆T就是以MN为直径过原点的圆,其方程为

(x-t)2+(y-h)2=t2+h2.

令x=t,有y2-2hy-t2=0.

所以yMyN=-t2.

由题P(xp,yM),Q(xQ,yN),

所以yMyN=y1y2=-t2.

即-2pn=-t2.

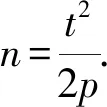
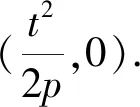
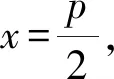
4 结束语

数学学科的关键能力有逻辑思维能力、运算求解能力、空间想象能力、数学建模能力和创新能力.为了考查数学关键能力,高考试题命制也以素养为导向,以培养关键能力为目标.就解析几何教学而言,教师不能仅仅作简单的解答分析和解答过程表述,更应该在深层次上重视知识的背景与关联、特殊与一般、类比与推广、来源与发展,才能有效培养学生更高的学科素养和关键能力,才能结合考题做到立德树人、服务选材、引导教学实现高考的核心功能[4].