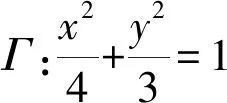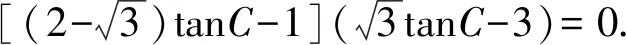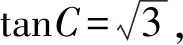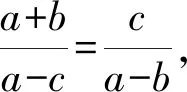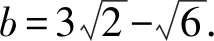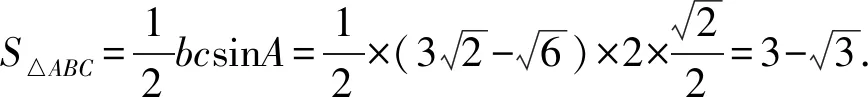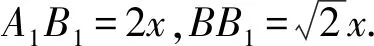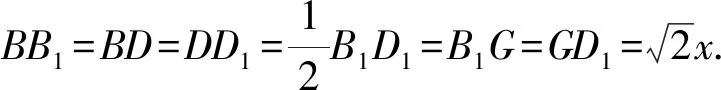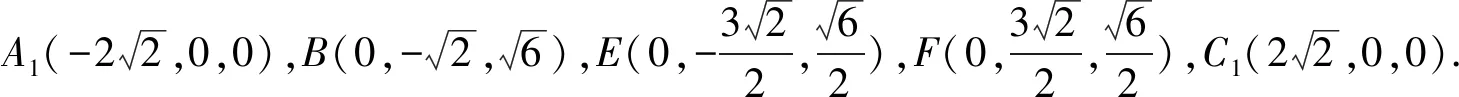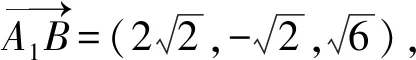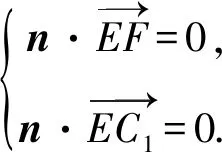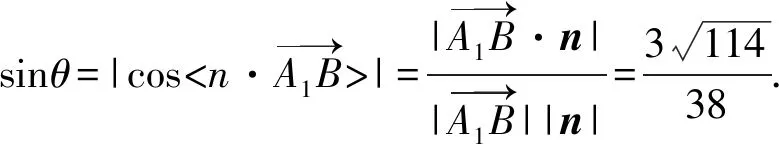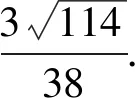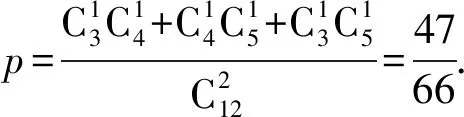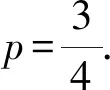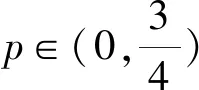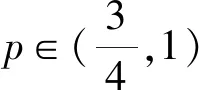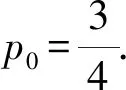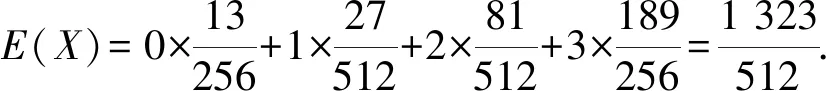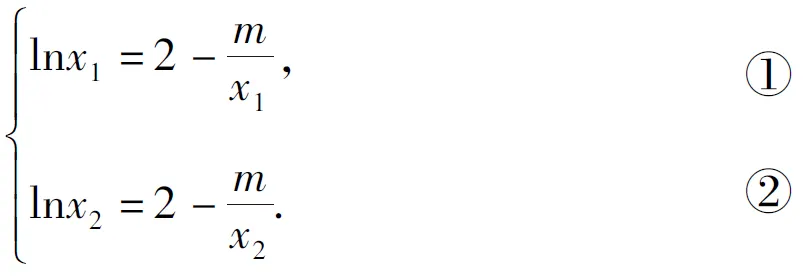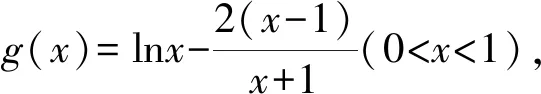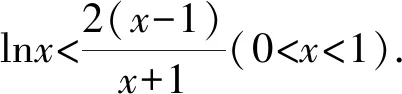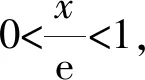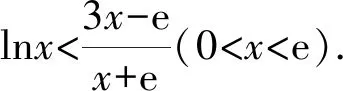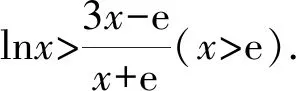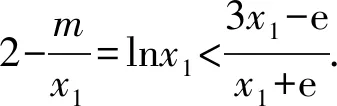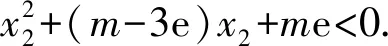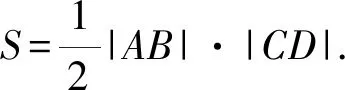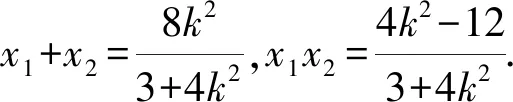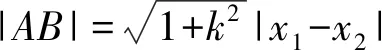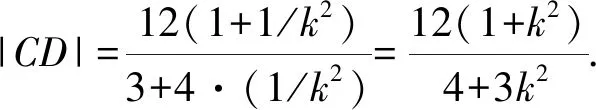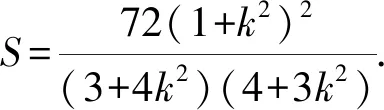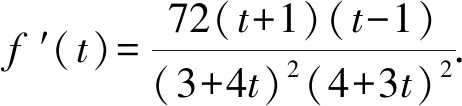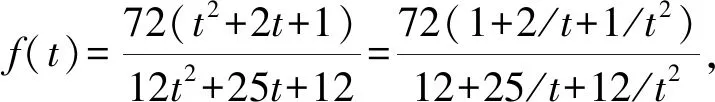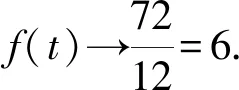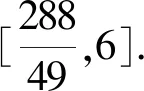2024年全国高考(新高考Ⅰ卷)数学模拟卷

李鸿昌

(北京师范大学贵阳附属中学,贵州 贵阳 550081)

一、选择题：本题共8小题,每小题5分,共40分.在每小题给出四个选项中,只有一项是符合题目要求的.

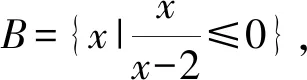
A.{0,1,2} B.[0,2) C.{0,1} D.[0,1)

A.第一象限 B.第二象限

C.第三象限 D.第四象限

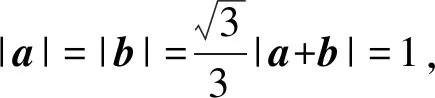
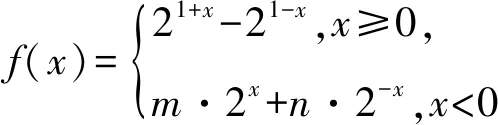
A.-4 B.-2 C.0 D.2

5.已知圆O的直径AB=6,动点M满足|MA|=2|MB|,若点M的轨迹为曲线C,曲线C与圆O相交于C,D两点,则|CD|=( ).

6.已知等差数列{an}的前n项和Sn有最大值, 若(a3-1)(a4-1)=2,S6=15,则Sn≥0时n的最大值为( ).

A.9 B.10 C.11 D.12

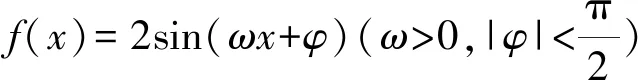
A.[7,11) B.[6,15)

C.[5,11) D.[6,12)

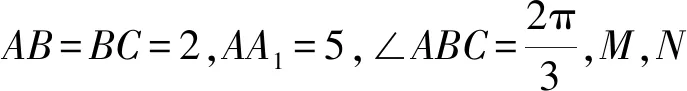
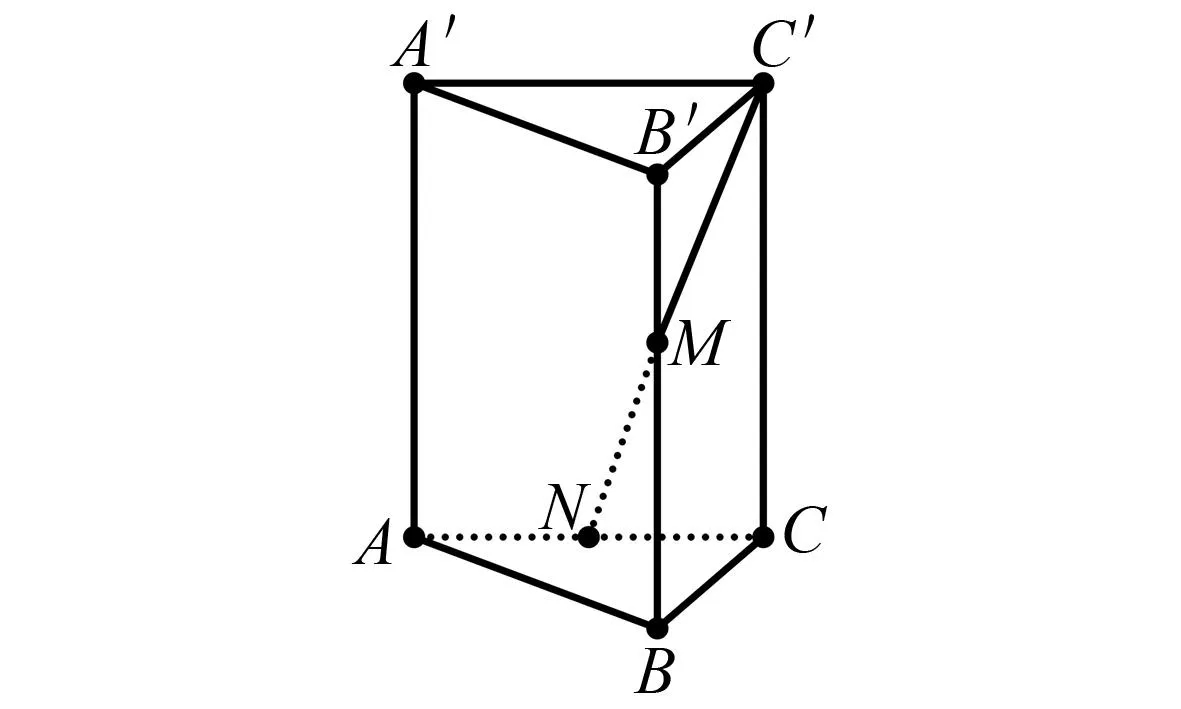
图1 第8题图

二、选择题：本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.

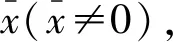
10.已知Р是圆O:x2+y2=1上的动点,直线l1:xcosθ+ysinθ=4与l2:xcosθ+ysinθ=2交于点Q,则( ).

A.l1与l2的距离为2

B.点P到直线l1距离的最大值为5

C.存在θ∈R,直线l2经过点P

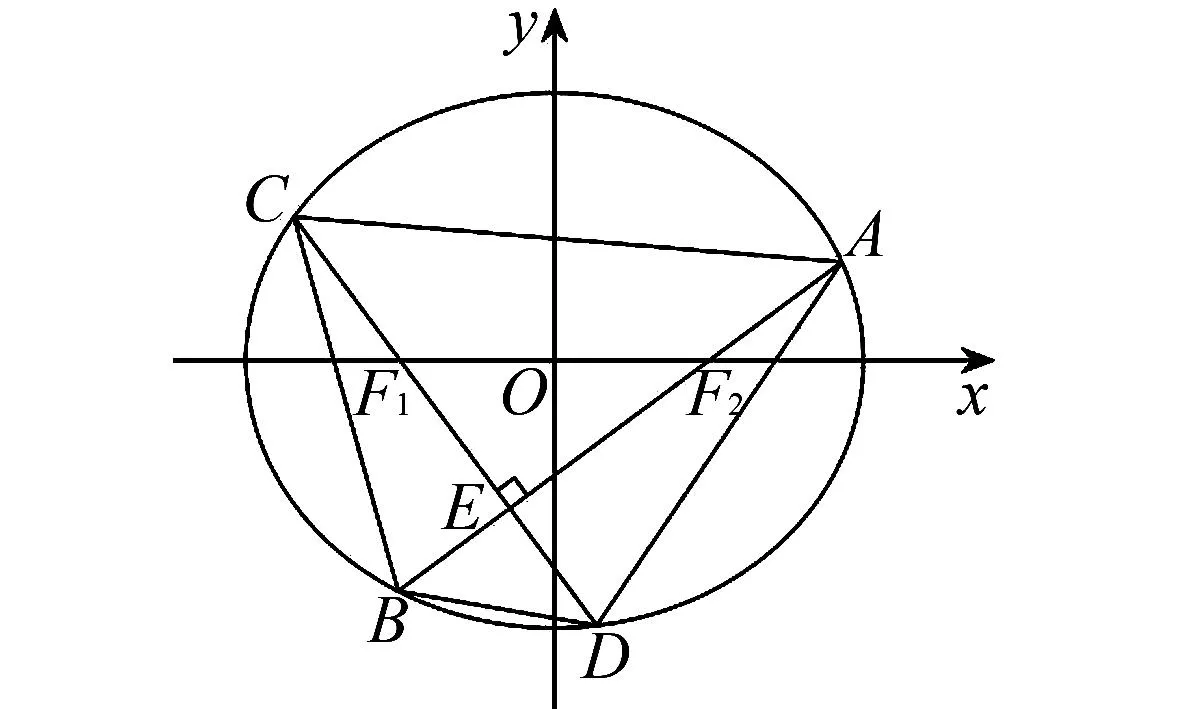
D.对任意的θ∈R,动点P到两直线l1,l2的距离以及l1与l2的距离之和的最大值为10

11.已知函数f(x)满足:①f(a+x)为偶函数;②f′(c+x)+f′(c-x)=2a,a≠c,其中f′(x)是f(x)的导函数,则下列结论正确的是( ).

A.f′(x)关于(a,0)对称

B.f(x)关于x=c对称

C.f(x)的一个周期为2|c-a|

D.f[f′(x)]关于x=c对称

三、填空题：本题共3小题,每小题5分,共15分.

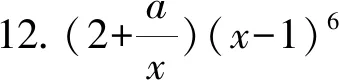
13.已知正六棱台ABCDEF-A1B1C1D1E1F1的上、下底面边长分别为3,4,该正六棱台的外接球的表面积为100π,则该正六棱台的高为____.

14.若直线ex-2y+eln 2=0是指数函数y=ax(a>0且a≠1)图象的一条切线,则实数a的值为____.

四、解答题：本题共5小题,共77分.解答应写出文字说明.证明过程或演算步骤.

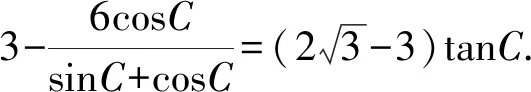
(1)求角C;

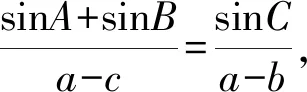
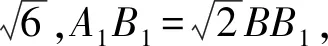
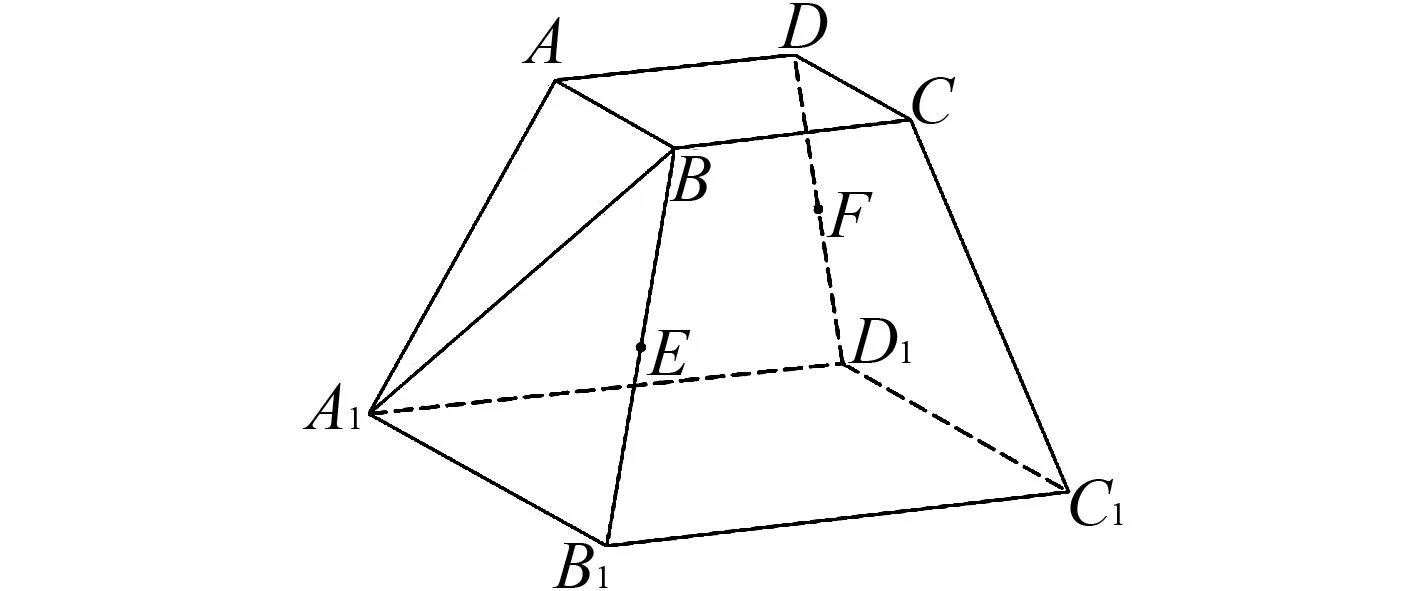
图2 第16题图

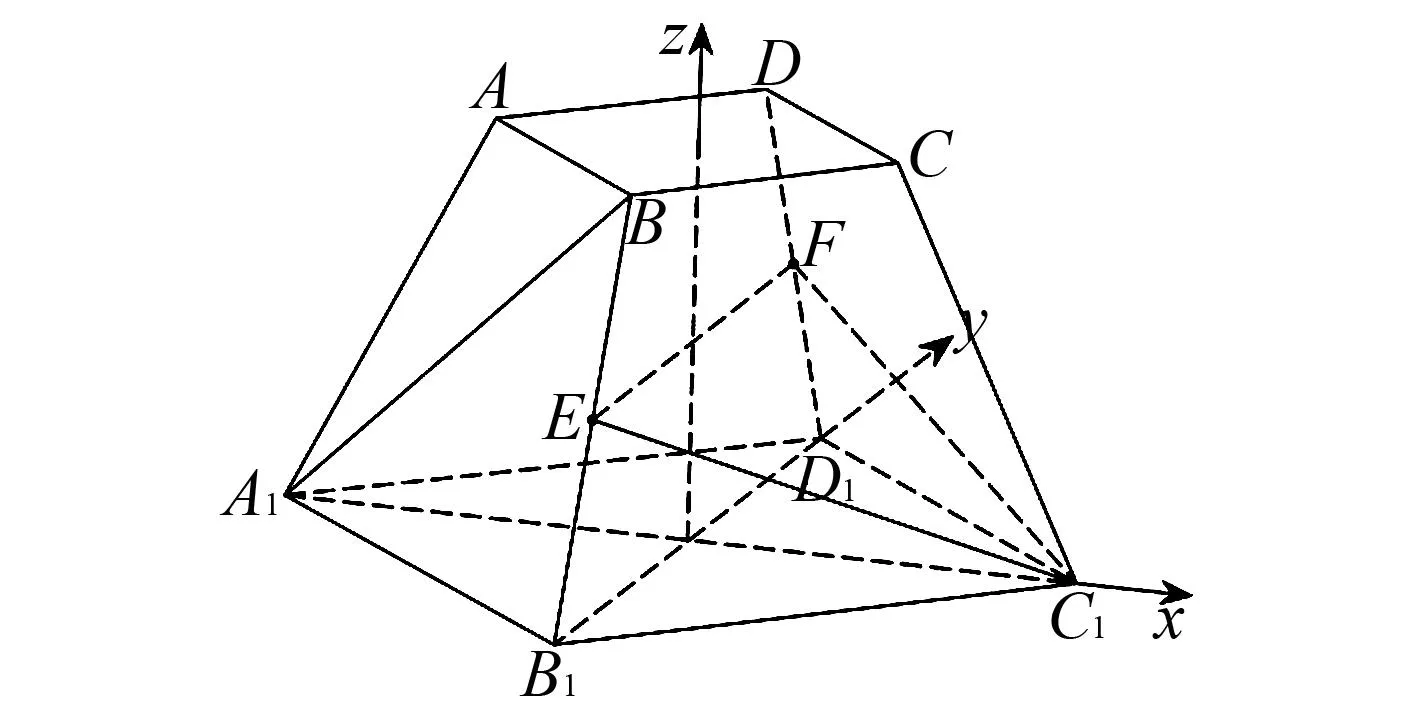
(1)求证:DB1⊥BA1;

(2)当点F移动到DD1的中点时,求BA1与平面C1EF夹角的正弦值.

17.杭州第19届亚运会于2023年9月23日在万众期待中开幕,乒乓球作为国球又一次掀起热潮.为推进素质教育某学校举行了乒乓球比赛,其中参加男子乒乓球决赛的12名队员来自3个不同校区,三个校区的队员人数分别是3,4,5.本次决赛的比赛赛制采取单循环方式,即每名队员进行11场比赛(每场比赛都采取5局3胜制),最后根据积分选出最后的冠军.积分规则如下:比赛中以3∶0或3∶1取胜的队员积3分,失败的队员积0分;而在比赛中以3∶2取胜的队员积2分,失败的队员积1分.已知第10轮张三对抗李四,设每局比赛张三取胜的概率均为p(0

(1)比赛结束后冠亚军(没有并列)恰好来自不同校区的概率是多少?

(2)第10轮比赛中,记张三3∶1取胜的概率为f(p).

①求出f(p)的最大值点p0;

②若以p0作为p的值,这轮比赛张三所得积分为X,求X的分布列及期望.

18.已知函数f(x)=xlnx-2x+m(m∈R)有两个零点x1,x2,且x1

(1)求m的取值范围;

(2)证明:x1+x2<3e-m.

(1)设AB与CD交于点E,求证:点E在椭圆Γ内;

(2)求四边形ACBD的面积的取值范围.

参考答案

1.C 2.D 3.A 4.A 5.D 6.C 7.A 8.D 9.BC 10.AB 11.AD

12.-3 13.1或7 14.e或e2

15.(1)由题意得

因为C∈(0,90°),所以C=60°或75°.

所以B=60°.

①若C=60°,易知△ABC为等边三角形.

②若C=75°,则A=45°.

16.(1)由题意可得平面AA1C1C与平面BB1D1D互相垂直.

因为A1C1⊥B1D1,所以A1C1⊥DB1.

所以四边形BB1GD为菱形.

所以BG⊥DB1.

又因为A1C1∩BG=G,

所以DB1⊥平面BA1C1.

又BA1⊂平面BA1C1,故DB1⊥BA1.

图3 正四棱锥建系

设平面C1EF的一个法向量为n=(x,y,z),

设BA1与平面C1EF的夹角为θ,

(2)①由题可知

f′(p)=3[3p2(1-p)+p3×(-1)]

=3p2(3-4p).

②X的可能取值为0,1,2,3.

所以X的分布列见表1:

表1X的分布列

X0123P132562751281512189256

18.(1)由题知f′(x)=lnx-1.

令f′(x)=0,得x=e.

当x∈(0,e)时,f′(x)<0,f(x)单调递减,

当x∈(e,+∞)时,f′(x)>0,f(x)单调递增.

所以f(x)min=f(e)=m-e.

要使f(x)有两个零点,则需满足m-e<0,解得m

且当x→0+时,f(x)→m,当x→+∞时,f(x)→+∞,故m>0.

综上所述,m的取值范围是(0,e).

(2)由(1)得0

所以g(x)在(0,1)单调递增.

即g(x)

整理,得x12+(m-3e)x1+me>0.

③

④

④-③整理,得

(x2-x1)[x2+x1-(3e-m)]<0.

又因为x2-x1>0,所以x1+x2<3e-m.

故原不等式得证.

19.(1)由题意知c2=a2-b2=4-3=1.

所以F1(-1,0),F2(1,0).

因为CD⊥AB,即F1E⊥F2E.

所以点E在以线段F1F2为直径的圆上,该圆的方程为x2+y2=1.

①若AB垂直于x轴,则CD为长轴,此时

②若AB和CD都不垂直于x轴,如图4所示.

图4 椭圆内接四边形

设AB的斜率为k(k≠0),则由

得(3+4k2)x2-8k2x+4k2-12=0.

记k2=t(t>0),构造函数

所以当x∈(0,1)时,f′(t)<0,f(t)单调递减;

当x∈(1,+∞)时,f′(t)>0,f(t)单调递增.

当t→0(t>0)时,f(t)→6;