用运动的分解法处理两道粒子摆线运动高考真题

罗 章 彭知文

(湖南师范大学附属中学,湖南 长沙 410006)

一个物体的实际运动往往同时参与几个运动,我们把这几个运动叫作实际运动的分运动,把这个实际运动叫作分运动的合运动.复杂的曲线运动往往不好理解或者定量分析,但是如果能化曲为直或者化繁为简,则有助于对物体运动的深入理解.解决带电粒子摆线运动的方法可称为“速度补偿法”,也称为“速度构造法”.这一方法将复杂的摆线运动分解为匀速圆周运动以及匀速直线运动[1].

1 问题的提出

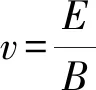
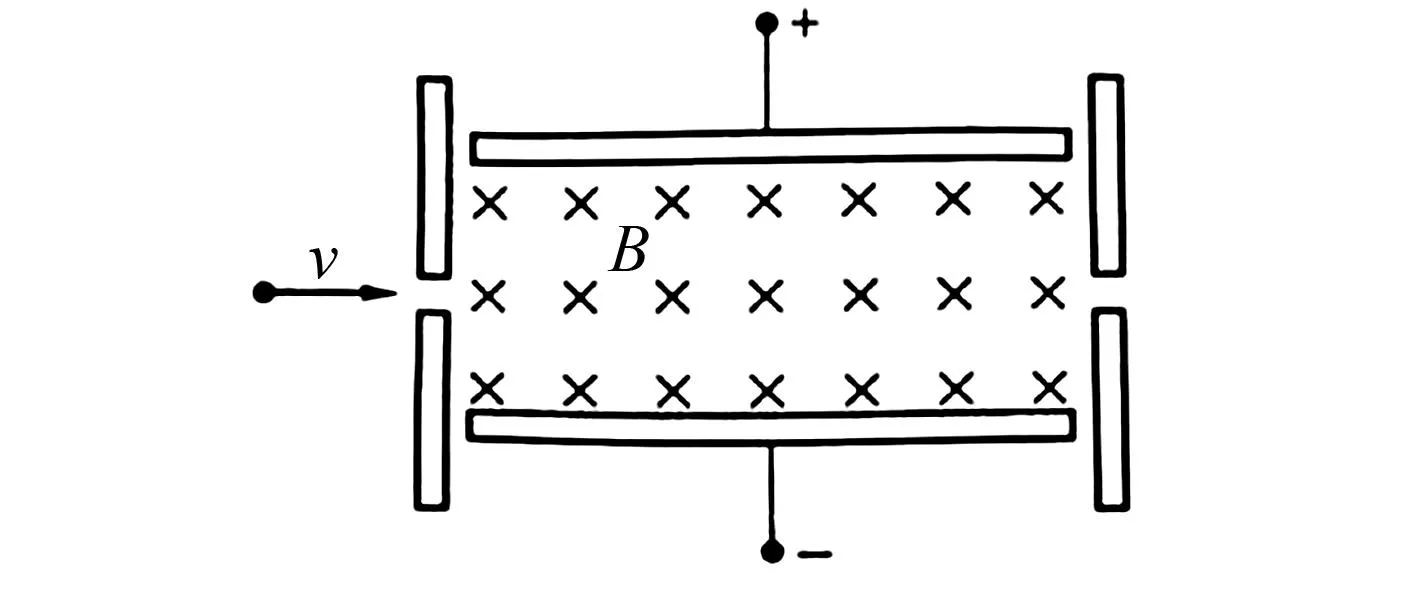
图1 速度选择器

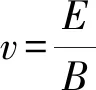
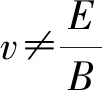
2 解决问题的办法

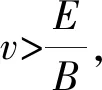
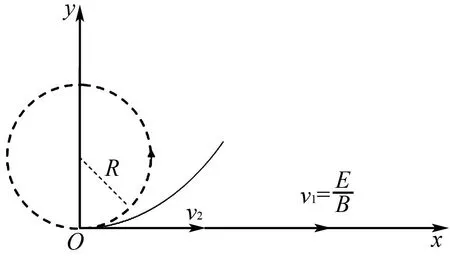
图2 运动的分解示意图

下面用此法来解决两道高考真题.

3 高考真题的处理

例1(2023年高考江苏卷)霍尔推进器某局部区域可抽象成如图3所示的模型.Oxy平面内存在竖直向下的匀强电场和垂直坐标平面向里的匀强磁场,磁感应强度为B.质量为m、电荷量为e的电子从O点沿x轴正方向水平入射.入射速度为v0时,电子沿x轴做直线运动;入射速度小于v0时,电子的运动轨迹如图3中的虚线所示,且在最高点与在最低点所受的合力大小相等.不计重力及电子间相互作用.

(1)求电场强度的大小E;

解析(1)由题知,入射速度为v0时,电子沿x轴做直线运动,则有eE=ev0B

解得:E=v0B

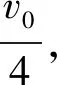
(3)若电子以v入射时,设电子能达到的最高点位置的纵坐标为y,则根据动能定理有

由于电子在最高点与在最低点所受的合力大小相等,则在最高点有F合=evmB-eE

在最低点有:F合=eE-evB

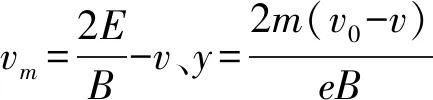
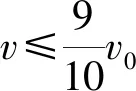
可以解得:v1=0.9v0.后续分析与前面相同.

例2(2013年高考福建卷)如图4,空间存在一范围足够大的垂直于xOy平面向外的匀强磁场,磁感应强度大小为B.让质量为m,电荷量为q(q>0)的粒子从坐标原点O沿xOy平面以不同的初速度大小和方向入射到该磁场中.不计重力和粒子间的影响.

图4 带电粒子在磁场中运动

(1)略;(2)略;(3)如图5所示,若在此空间再加入沿y正向、大小为E的匀强电场,一粒子从O点以初速度v0沿y轴正方向发射.研究表明:粒子在xOy平面内做周期性运动,且在任一时刻,粒子速度的x分量vx与其所在位置的坐标成正比,比例系数与电场强度大小E无关.求该粒子运动过程中的最大速度vm.

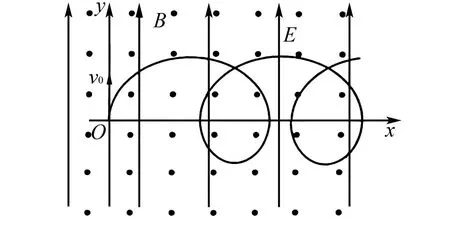
图5 带电粒子在复合场中运动

解析带电粒子的初速度v0沿y轴正方向,而在x轴方向上速度为零.我们可以将速度为“零”分解为向右和向左的两个等大反向的速度,向右的速度产生的洛伦兹力与电场力平衡,则:qv右B=qE

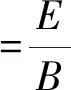
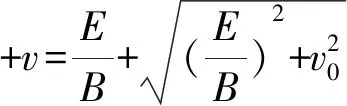
采用“零”分解法处理该题,巧妙地将复杂的螺旋线运动等效为匀速直线运动与匀速圆周运动的合成,直观而且深刻.

4 结束语

带电粒子在复合场中的运动是一类相当复杂的问题,尤其是做摆线或滚轮线运动,还经常出现在高考真题中,用以考查学生的核心素养.处理这类运动通常有“运动的分解与合成法”和“相对运动法”以及“微积分法”.用中学生普遍易于接受的运动的合成与分解的角度展开分析:确定分运动为圆周运动的分速度的方向,从而得出初末位置及速度偏转角,进而得出运动时间和两分运动的分位移[2].本文提供了快速解答2023年和2013年高考真题的思路.