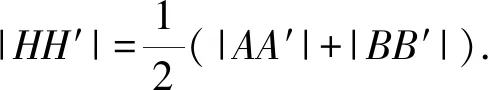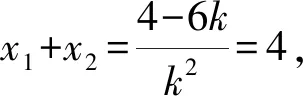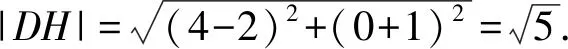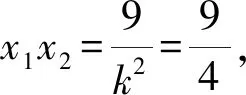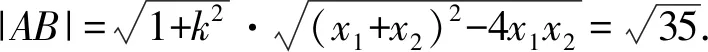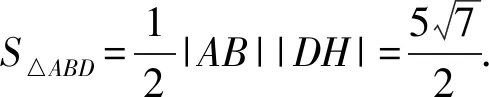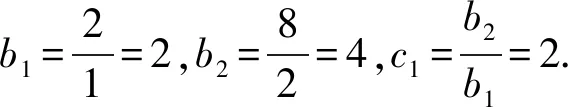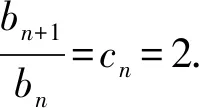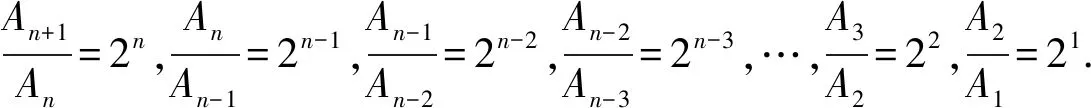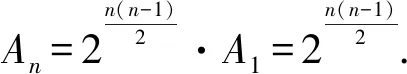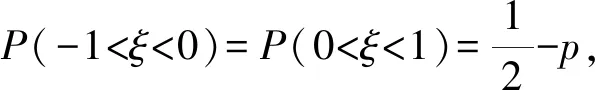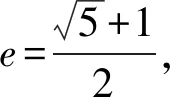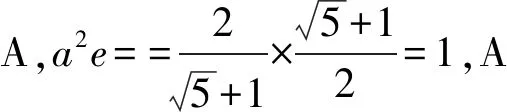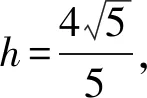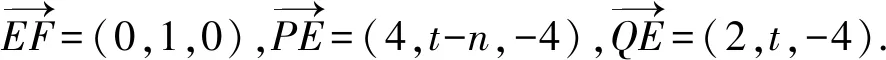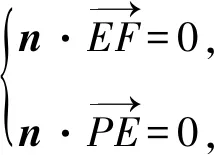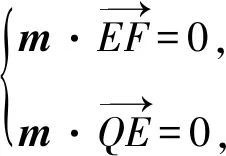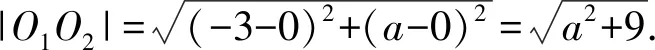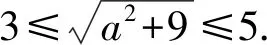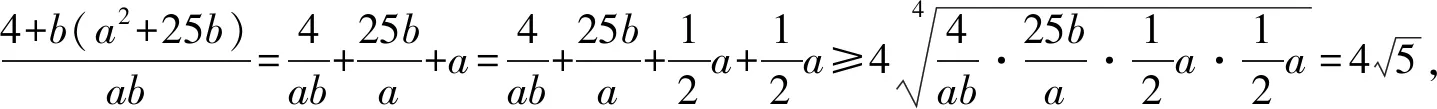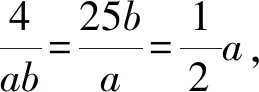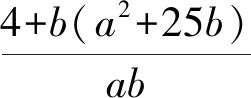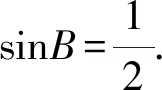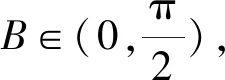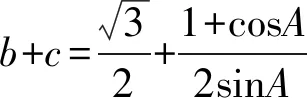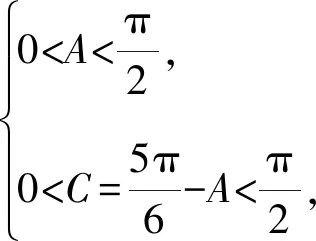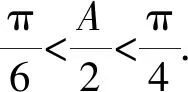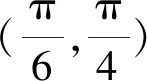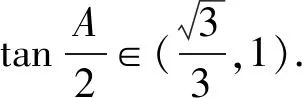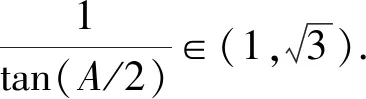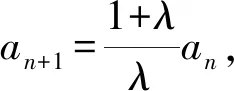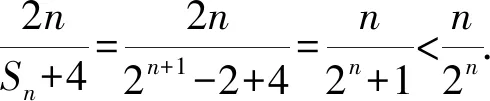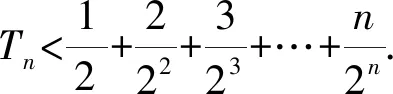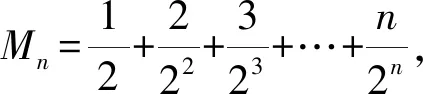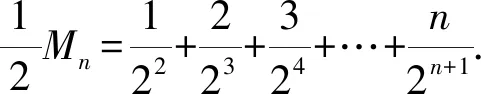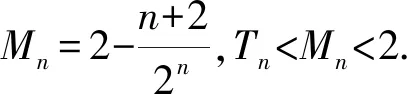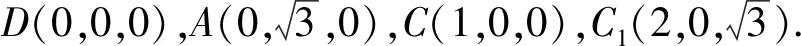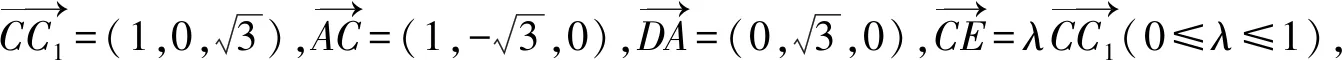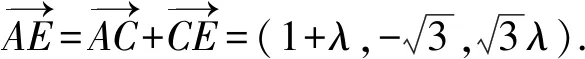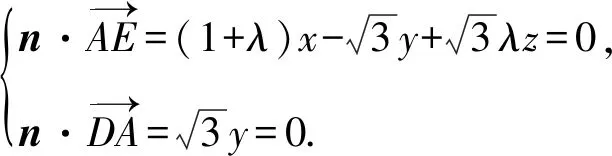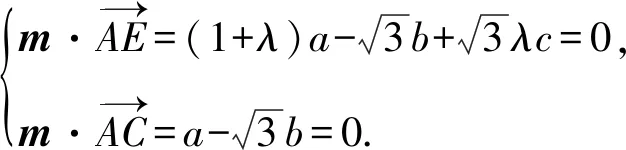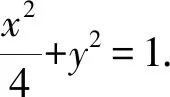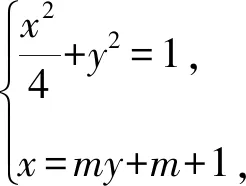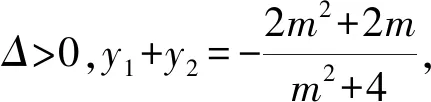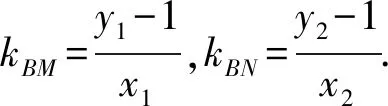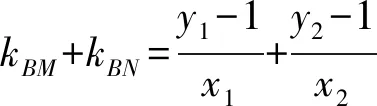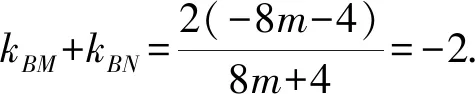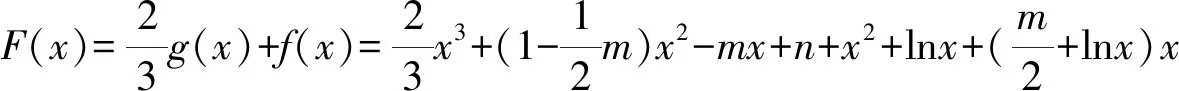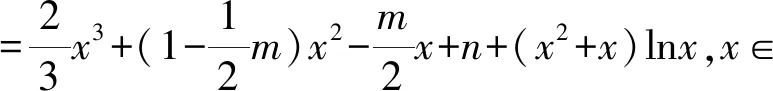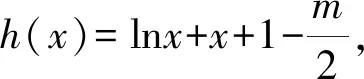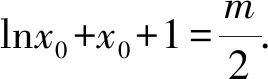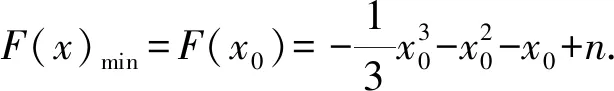2024年新高考数学模拟卷(五)

李春林

(天水市第九中学,甘肃 天水 741020)

(河南、山西、江西、安徽、甘肃、青海、内蒙古、黑龙江、吉林、宁夏、新疆、陕西)

第Ⅰ卷(选择题)

一、选择题：本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.

1.设集合A={x|2x<-x+1},B={x∈Z|ln(-x)<1},则A∩B等于( ).

A.(-e,+∞) B.(-e,0)

C.{-3,-2,-1} D.{-2,-1}

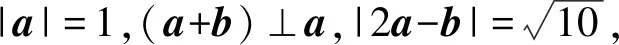
A.充分不必要条件 B.必要不充分条件

C.充要条件 D.既不充分也不必要条件

5.函数f(x)=(elog2|x|-e-log2|x|)·sinx在区间[-π,π]上的图象大致为( ).

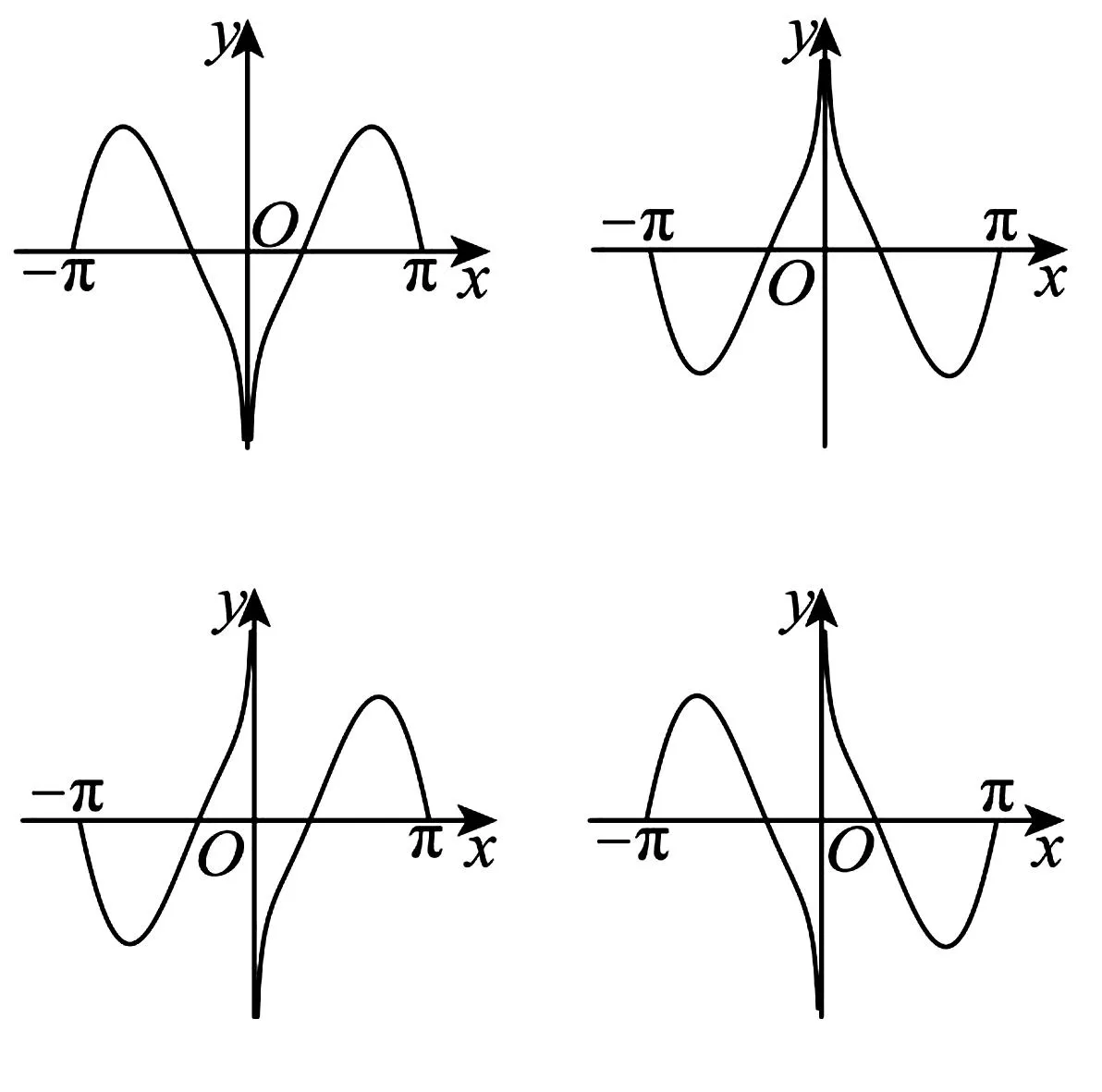
6.若(2x-1)10=a0+a1(x-1)+a2(x-1)2+…+a10(x-1)10,则a1+2a2+…+10a10=( ).

A.310B.310-1 C.20×39D.10×39

7.已知抛物线C:y2=4x的焦点为F,过点(0,3)的直线与C交于A,B两点,线段AB的垂直平分线与x轴交于点D,若AF+BF=6,则△ABD的面积为( ).

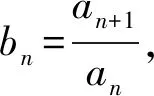
A.215B.219C.221D.228

二、多选题：本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.

9.下列关于概率统计说法中正确的是( ).

A.两个变量x,y的相关系数为r,则|r|越小,x与y之间的相关性越弱

B.设随机变量ξ服从正态分布N(0,1),若P(ξ>1)=p,则P(-1<ξ<0)=1-2p

C.在回归分析中,R2为0.99的模型比R2为0.88的模型拟合得更好

D.某人在10次答题中,答对题数为X,X～B(10,0.7),则答对7题的概率最大

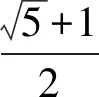
A.a2e=1

B.顶点到渐近线的距离为e

C.A2B⊥FB

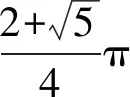
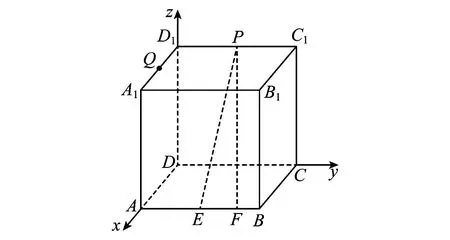
11.已知正方体ABCD-A1B1C1D1的棱长为4,EF是棱AB上的一条线段,且EF=1,点Q是棱A1D1的中点,点P是棱C1D1上的动点,则下面结论中正确的是( ).

A.PQ与EF一定不垂直

第Ⅱ卷(非选择题)

三、填空题：本题共3小题,每小题5分,共15分.

12.已知圆O1:x2+y2=1,圆O2:(x+3)2+(y-a)2=16,如果这两个圆有公共点,则实数a的取值范围是____.

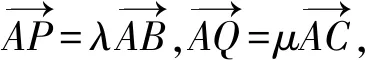
四、解答题：本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.

15.已知锐角△ABC的内角A,B,C的对边分别为a,b,c,且满足(2sinA-cosC)b=ccosB.

(1)求B;

(2)若a=1,求b+c的取值范围.

16.已知数列{an}的前n项和为Sn,a1=2,λan+1=Sn+2,n∈N*.

(1)是否存在实数λ,使得数列{an}为等比数列?若存在,求出λ的值;若不存在,说明理由;

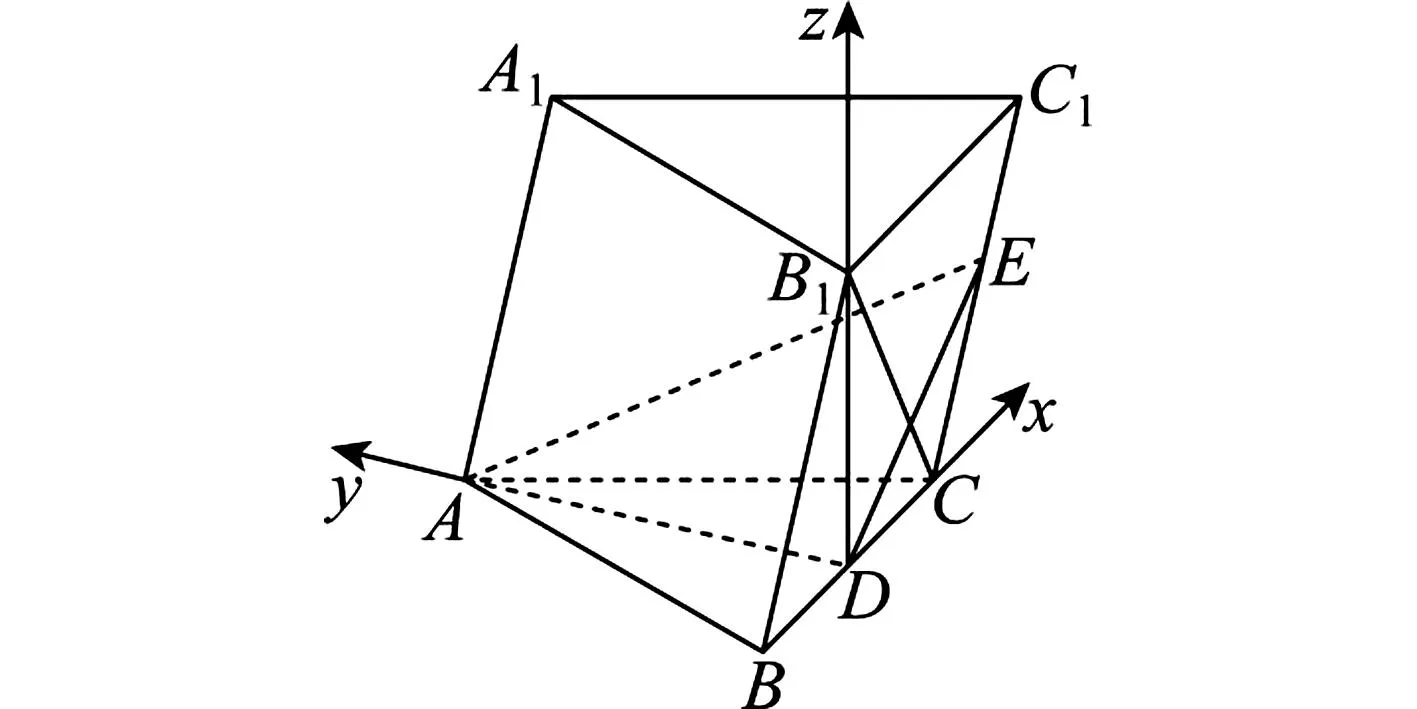
17.如图1,在三棱柱ABC-A1B1C1中,AB=AC=2,D为BC的中点,平面BB1C1C⊥平面ABC.

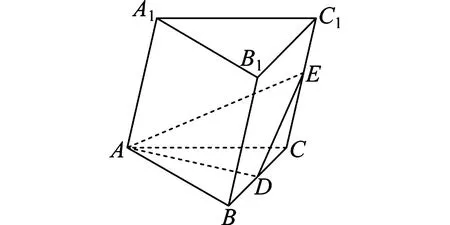
图1 第17题图

(1)证明:AD⊥BB1;

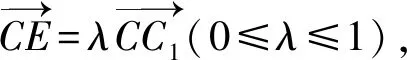
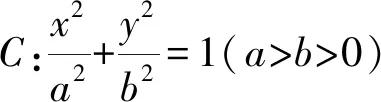
(1)求椭圆C的方程;

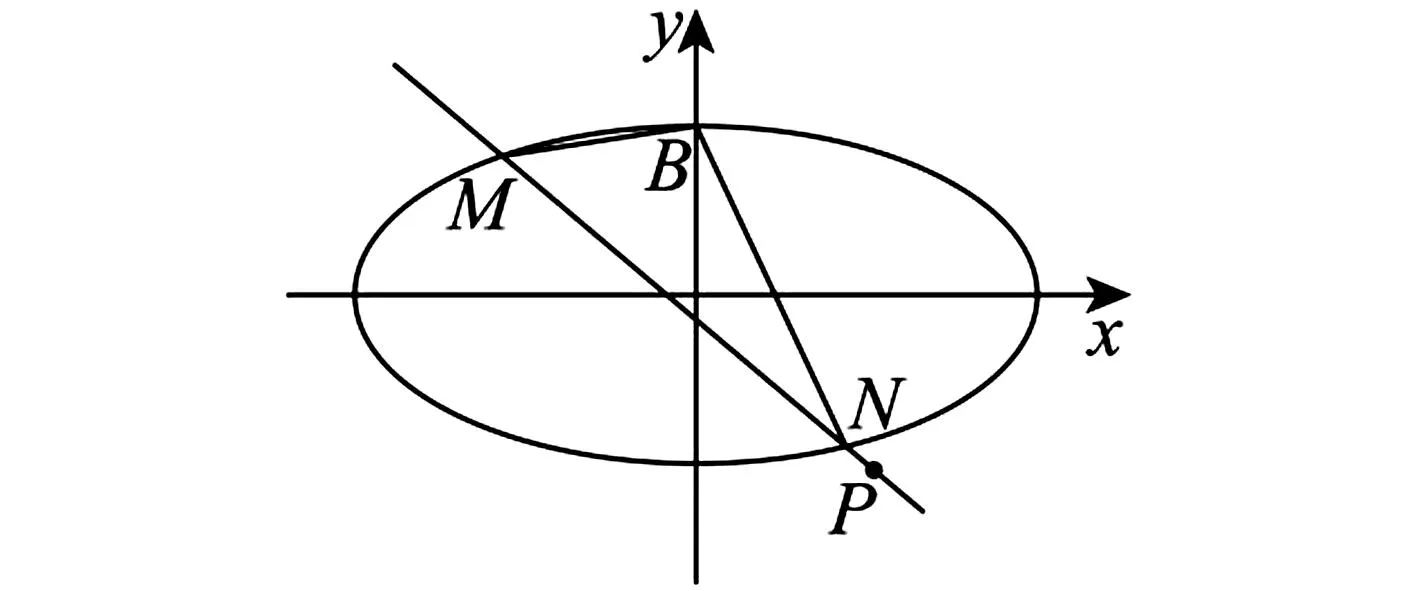
(2)过点P(1,-1)的直线l与椭圆C相交于M,N两点,设点B(0,1),求证:直线BM,BN的斜率之和kBM+kBN为定值,并求出定值.

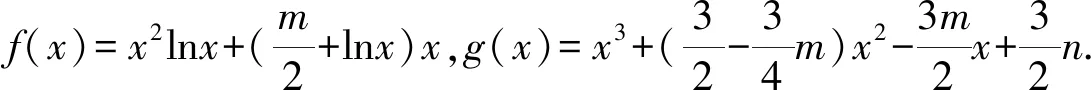
(1)当m=0时,求f(x)在(1,f(1))处的切线方程;

参考答案

1.由题意得,A={x|2x+x<1}.

因为20+0=1,y=2x+x在(-∞,+∞)单调递增,所以A={x|x<0},B={x∈Z|ln(-x)<1}={x∈Z|0<-x

所以A∩B={-2,-1}.

故选D.

故选A.

(a+b)·a=a2+a·b=1+a·b=0.

所以a·b=-1.

所以|2a-b|2=4a2-4a·b+b2=10.

故选B.

4.若角α的终边经过点P(1,2),

综上,p是q的充分不必要条件.

故选A.

5.因为f(-x)=(elog2|-x|-e-log2|-x|)·sin(-x)=-(elog2|x|-e-log2|x|)·sinx=-f(x),

所以f(x)为奇函数.

当0

所以elog2|x|

又sinx>0,所以f(x)<0.

故选C.

6.根据题意,对原式两边求导可得:

令x=2,可得20×39=a1+2a2+…+10a10.

故选C.

由抛物线的定义可知,

|AF|=|AA′|,|BF|=|BB′|,|AF|+|BF|=6.

所以|AA′|+|BB′|=6.得|HH′|=3.

即点H的横坐标为2.

设直线AB:y=kx+3,代入抛物线方程,得

k2x2+(6k-4)x+9=0.

所以直线AB:y=-2x+3,H(2,-1).

令y=0,解得x=4,即D(4,0).

故选C.

又数列{An}的二阶商数列{cn}是常数列,则cn=c1=2.

则数列{bn}是2为首项,2为公比的等比数列.

则bn=2·2n-1=2n.

等式左右分别相乘可得

故选C.

9.对于A,两个变量x,y的相关系数为r,|r|越小,x与y之间的相关性越弱,故A正确;

对于C,R2越接近1,模型拟合越好,且0.99>0.88,故C正确;

对于D,因为X～B(10,0.7),则数学期望为10×0.7=7,说明答对7题的概率最大,故D正确.

故选ACD

故选ACD.

11.对于A,当点P与点D1重合时,由正方体的性质易得PQ⊥面ABB1A1,而EF⊂面ABB1A1,所以PQ⊥EF,故A错误;

对于C,由于平面PEF就是平面ABC1D1,

设点P到平面QEF的距离为h,

图2 第11题解析图

设平面PEF的法向量为n=(x1,y1,z1),

令x1=1,则n=(1,0,1).

设平面QEF的法向量为m=(x2,y2,z2),

令x2=2,则m=(2,0,1).

设二面角P-EF-Q的平面角为α,

故选BCD.

12.由题意知,O1(0,0),r1=1,O2(-3,a),r2=4.

因为圆O1与圆O2有公共点,

所以r2-r1≤|O1O2|≤r2+r1.

解得-4≤a≤4.

所以实数a的取值范围是[-4,4].

13.因为a>0,b>0,

如图3所示,延长AG交BC于点D,则D是BC中点,

图3 第14题解析图

又P,G,Q三点共线,

15.(1)由正弦定理,得

2sinAsinB-sinBcosC=sinCcosB.

即2sinAsinB=sin(B+C)=sinA.

由△ABC是锐角三角形可得

16.(1)由题知λan+1=Sn+2,

①

当n≥2时,λan=Sn-1+2.

②

两式相减,得λan+1-λan=an.

即λan+1=(1+λ)an.

当λ=0时,an=0,不能使得数列{an}为等比数列,舍去,

当λ=-1时,an+1=0·an=0,不能使得数列{an}为等比数列,舍去,

当λ∈(-∞,-1)∪(-1,0)∪(0,+∞)时,数列{an}为等比数列.

(2)当λ=1时,an+1=2an,

故{an}为首项为2,公比为2的等比数列.

两式相减,得

17.(1)因为AB=AC,且D为BC的中点,则AD⊥BC.

因为平面BB1C1C⊥平面ABC,交线为BC,AD⊥BC,AD⊂平面ABC,

可得AD⊥平面BB1C1C,且BB1⊂平面BB1C1C.

所以AD⊥BB1.

(2)连接B1D,B1C,

因为四边形BB1C1C为边长为2的菱形,且∠B1BC=60°,

可知△B1BC为等边三角形,且D为BC的中点,则B1D⊥BC.

又因为平面BB1C1C⊥平面ABC,交线为BC,B1D⊂平面BB1C1C,

所以B1D⊥平面ABC.

以D为原点,DC,DA,DB1分别为x,y,z轴建立空间直角坐标系,如图4.

图4 第17题解析图

设平面AED的一个法向量为n=(x,y,z),则

设平面AEC的一个法向量为m=(a,b,c),则

设平面EAD与平面EAC的夹角为θ,

设R到F1F2的距离为d,因为|F1F2|=2c,

易得当d=b时△RF1F2面积取得最大值.

因为b2=a2-c2,

所以a2=4,b2=1.

(2)如图5,易知点P在椭圆外.

图5 第18题解析图

(m2+4)y2+(2m2+2m)y+m2+2m-3=0.

所以kBM+kBN

19.(1)因为m=0,

所以f(x)=x2lnx+xlnx,x∈(0,+∞).

所以f(1)=0.

所以f′(x)=(2x+1)lnx+x+1.

所以f′(1)=2.

所以f(x)在(1,0)处的切线方程为y-0=2(x-1),即2x-y-2=0.

则h(x)在(0,+∞)上单调递增.

当x→0时h(x)→-∞,当x→+∞时h(x)→+∞,

故存在唯一x0使得h(x0)=0.

则当x∈(0,x0)时h(x)<0,即F′(x)<0.

所以F(x)在(0,x0)上单调递减.

当x∈(x0,+∞)时h(x)>0,即F′(x)>0.

所以F(x)在(x0,+∞)上单调递增.

所以F(x)min=F(x0)≥0.

所以当0

即t(x)在(0,1)上单调递减.

当x>1时t′(x)>0,即t(x)在(1,+∞)上单调递增.