2024届高考数学模拟试卷(新高考Ⅰ卷)

王东海

(安徽省合肥市肥东县城关中学,安徽 合肥 231600)

第Ⅰ卷(选择题)

一、单选题:本题共8小题,共40分.在每小题列出的选项中,选出符合的一项.

1.已知集合A={y|y=2x-1,x∈R},B={x|x2-x-2<0},则( ).

C.A∪B=AD.A∩(RB)=A

3.已知平面向量a=(1,m),b=(0,2),若b⊥(3a-mb),则实数m=( ).

A.-1 B.0 C.1 D.2

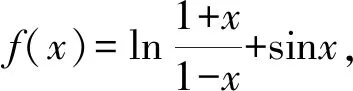
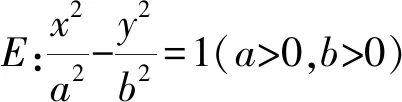
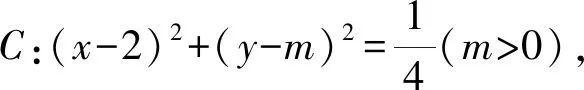
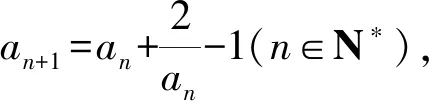
A.充要条件 B.充分不必要条件

C.必要不充分条件 D.既不充分也不必要条件

二、多选题：本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.

9.若甲组样本数据x1,x2,…,xn(数据各不相同)的平均数为3,乙组样本数据2x1+a,2x2+a,…,2xn+a的平均数为5,下列说法错误的是( ).

A.a的值不确定

B.乙组样本数据的方差为甲组样本数据方差的2倍

C.两组样本数据的极差可能相等

D.两组样本数据的中位数可能相等

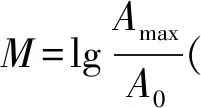
A.若地震震级M增加1级,则最大振幅Amax增加到原来的10倍

B.若地震震级M增加1级,则放出的能量E增加到原来的10倍

C.若最大振幅Amax增加到原来的100倍,则放出的能量E也增加到原来的100倍

D.若最大振幅Amax增加到原来的100倍,则放出的能量E增加到原来的1 000倍

11.如图1所示,在棱长为1的正方体ABCD—A1B1C1D中,E为侧面BCC1B1的中心,F是棱C1D1的中点,若点P为线段BD1上的动点,N为ABCD所在平面内的动点,则下列说法正确的是( ).

图1 第11题图

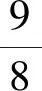
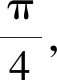
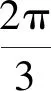
第Ⅱ卷(非选择题)

三、填空题：本题共3小题,每小题5分,共15分.

12.某校在新学期开设了“遇见GGB”“数学与生活”“微积分初步”“无限的世界”和“数学阅读与写作”5门数学类校本课程.小明和小华两位同学商量每人选报2门校本课程.若两人所选的课程至多有一门相同,且小明一定选报“遇见GGB”课程,则两位同学不同的选课方案有____种.(用数字作答)

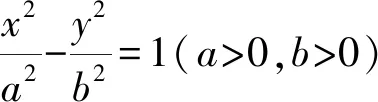
四、解答题：本题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤

(1)求角C的大小;

(2)若△ABC为锐角三角形,且b=2,求△ABC周长的取值范围.

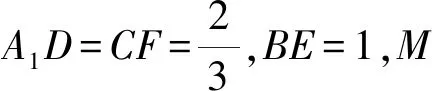
图2 第16题图

(1)证明:BM∥平面DEF;

(2)点P在棱BB1上,当二面角P-DF-E为30°时,求EP的长.

(1)当a=1时,求函数f(x)的单调区间;

(2)求证:当a>0时,f(x)≤e2a-2.

18.已知数列{an}满足a1=1,an+1=3an+2,n∈N*,数列{bn}满足b1=1,Sn+1-n=Sn+bn+n+1,其中Sn为数列{bn}的前n项和.

(1)求数列{an},{bn}的通项公式;

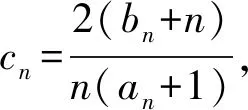
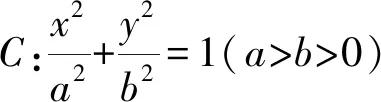
(1)求椭圆C的标准方程;

参考答案

1.C 2.D 3.B 4.C 5.C 6.D 7.A

8.B 9.ABC 10.AD 11.BCD

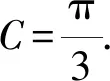
因为△ABC为锐角三角形,

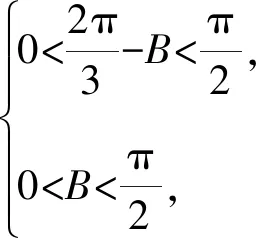
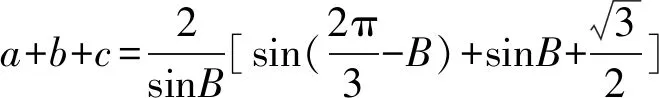
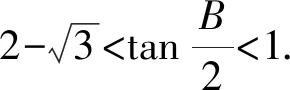
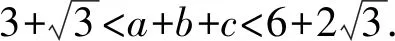
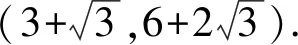
16.(1)取DF中点N,连接EN,MN,由MN为梯形ADFC的中位线,得

又BE∥AD,故MN∥BE,且MN=BE.

故四边形BMNE为平行四边形,则BM∥NE.

因为NE⊂平面DEF,BM⊄平面DEF,

故BM∥平面DEF.

(2)以BM所在直线为x轴,AC所在直线为y轴,MN所在直线为z轴,建立空间直角坐标系M-xyz,如图3所示,

图3 第16题解析图

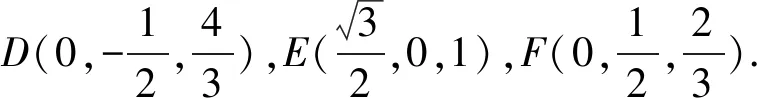
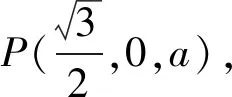
设平面DEF的法向量为n1=(x1,y1,z1),平面PDF的法向量为n2=(x2,y2,z2),

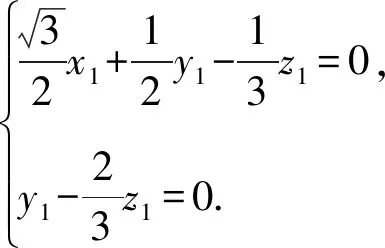
取z1=3,则y1=2,x1=0,得n1=(0,2,3).

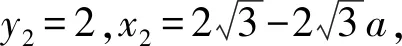
由二面角P-DF-E为30°,得

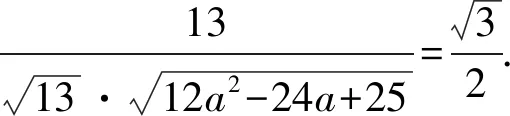
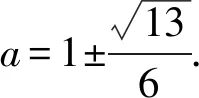
因为a>0,所以当x∈(0,e1-a)时,f′(x)>0,f(x)单调递增,当x∈(e1-a,+∞)时,f′(x)<0,f(x)单调递减.

即证:ea-1≥a.

记g(a)=ea-1-a,则g′(a)=ea-1-1,当a∈(0,1)时,g′(a)<0,g(a)单调递减,当a∈(1,+∞)时,g′(a)>0,g(a)单调递增.

所以g(a)min=g(1)=0.

所以g(a)≥0恒成立,即ea-1≥a.

所以当a>0时,f(x)≤e2a-2.

18.(1)由an+1=3an+2,可得

an+1+1=3(an+1).

所以数列{an+1}是首项为a1+1=2,公比为3的等比数列.

所以an+1=2·3n-1.

所以数列{an}的通项公式为an=2·3n-1-1.

因为Sn+1-n=Sn+bn+n+1,

所以bn+1=bn+2n+1.

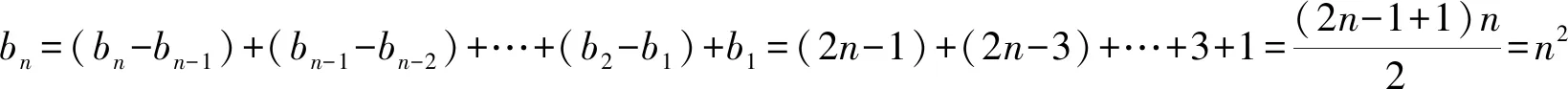
所以数列{bn}的通项公式为bn=n2.

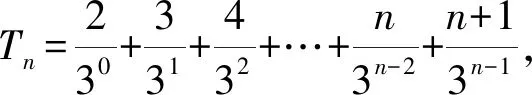
①

②

②-①,得

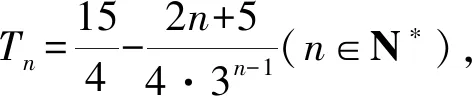
所以{Tn}是递增数列.

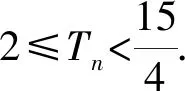
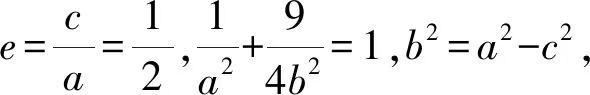
(2)由题意可知直线l的斜率k存在且k<0,设直线l方程为y=k(x-1),代入椭圆方程为

(3+4k2)x2-8k2x+4k2-12=0.

显然Δ>0恒成立.

设M(x1,y1),N(x2,y2),则

过点M,N分别作y轴的垂线,垂足分别为M′,N′,设原点为O,则