基于声子晶体的声发射波源检测概率研究

李红豫, 曾祥兴, 张 璐

(桂林理工大学 土木与建筑工程学院,桂林 541004)

声发射是材料或结构在外部荷载作用下,产生变形或断裂时,以弹性波的形式释放出应变能的现象;利用专业仪器可以采集并分析信号来评价材料或结构的损伤程度[1-2],声发射技术的核心优势在于可以通过采集和分析声发射信号来实现实时监测[3-4]、损伤评估和精准定位等。声发射技术是一种动态量测方法,探测到的声发射能量直接来自被测物体的损伤及材料特性改变,可提供缺陷随载荷、时间、温度等外部变量变化而变化的连续实时信息,因此,声发射技术能直接反映和评价结构或材料中的缺陷状态及损伤演化情况。该技术受构件的几何形状响应小,几乎可用于任何形状复杂的结构。但是声发射技术也有很大的局限性[5],如声发射能量衰减,检测区域有限,易受环境噪声影响和信号源未知而引起的数据分析复杂等,这些缺点严重制约着声发射技术的广泛应用,其中声发射信号是直接反映声发射源的行为,而这种声发射源的不确定性直接影响了声发射检测的可靠性。而在声发射技术应用和研究阶段,其检测可靠性往往会被忽视,从而严重影响声发射检测数据的有效性。

声发射技术通过接收声发射源的信号来研究材料的损伤状态,相较于其它的检测方法,声发射技术对缺陷具有更高的灵敏度,能够检测到零点几毫米下的裂缝扩展。以往关于声发射源研究主要在声发射源的定位上[6-9],对识别声发射源的研究较少,这使得声发射源严重影响了声发射的检测可靠性。检测可靠性一般用检测概率(probability of detection,POD)来评估,传统定义的检测概率是根据直接测量统计确定的,利用一系列包含缺陷的样品,在实际条件下进行检测,通过分析采集数据计算缺陷率的方式以评估检测概率。由于传统方法所花费的时间和费用较高,后来的研究更多开始向着通过建立模型辅助评价检测概率的研究方向发展。考虑到检测概率是评价检测是否可靠的量化依据,检测概率成为无损检测领域的重点研究方向之一。其中,在超声波领域中普遍出现了关于模型辅助检测概率方法的研究,以及使用模型辅助开发检测概率曲线的健康监测的研究[10-11]。Ogilvy[12]用超声波检测研究了一种预测平面缺陷的理论检测概率的数学模型,根据缺陷信号超过指定阈值的可能性,得出检测能力,该模型还可以研究缺陷参数的不确定性的影响,如方向、尺寸、粗糙度或在试样中的位置,然后通过计算它们的分布就可以确定最低可能的检测概率。Subair等[13]使用有限元仿真对不锈钢板中表面断裂纵向凹口进行超声脉冲回波检测,预测出不锈钢板和焊缝超声检测的检测概率曲线,确定了影响实际超声检测不确定性的主要参数(频率、楔角、缺陷尺寸等)并实现组合。Guan等[14]分别使用统计参数识别和模型辅助检测概率对与疲劳模型参数和缺陷尺寸相关的不确定性进行了量化,系统地分析了不确定变量的总体影响并通过对不确定变量的管理和减少相结合,降低评估风险。在声呐技术领域,夏志军等[15]建立了主、被动声呐检测模型,通过仿真分析了跃变层深度、声速差对声呐检测概率的影响。高飞等[16]建立被动声呐探测概率模型,利用声学实测数据,综合考虑传播损失、环境噪声、水文环境分布及季节变化,研究温跃层垂直分布及季节变化对声呐检测概率的影响。Guo等[17]基于接收机工作特性曲线、传播特性曲线和无源声呐方程,构建了探测概率与无源声呐探测范围之间的关系。在雷达技术领域,检测概率模型的建立探索[18-19]和其对应的影响参数的确定[20-21]都是量化检测概率的重要研究内容。

但是,以上的检测概率研究针对的都是主动技术,如超声波、雷达和声呐技术,主动技术的波源函数和波源本身位置是已知确定的,大大降低了波传递的理论分析难度,因此主动技术中检测概率的确定较为简单。而声发射作为一种被动方法,波源函数和具体位置是未知的,且蕴含的大量的损伤信息,是声发射检测中最关键的参数之一。以往关于声发射检测概率的问题并没有引起学术界的广泛关注,为了解决声发射检测概率计算问题,韩晖等研究出一定长度下疲劳裂缝的检测概率及结构起裂时对应声发射的阈值及其对损伤判断的影响,为减少金属疲劳损伤信号误判,提高检测效率提供支持[22]。Pollock[23]开发了一个利用声发射检测缺陷概率的模型,并测试了初始裂缝、衰减、信号源位置等参数对声发射检测概率的影响,为声发射与其他无损检测方法的更好整合开辟道路。Sause等[24]以衰减的试验测量为基础,用两种不同的方法演示了在信号传播距离上可检测信号的演算,研究了衰减效应与声发射检测概率的关系。上述关于声发射的检测概率研究中,大部分学者的研究重点普遍在材料和传播路径上,针对声发射信号源的检测概率研究较少,而声发射波源特性又直接影响着声发射信号特性,对于检测可靠性有着直接的影响。为了解决声发射波源的检测概率问题,本文基于声子晶体的滤噪原理,提出一种评估声发射波源检测概率的方法。

超材料滤波的概念是在19世纪初为了有效控制电磁波而产生,最早应用于研发微波雷达吸收器(microwave radar absorbers)上;声子晶体是由弹性固体周期排列在另一种固体或流体介质中形成的一种新型功能材料,针对弹性波的传递问题,通过改变周期性布置和材料组合而实现带隙或者信号放大的作用[25]。其中,为了滤除声发射噪声,可以利用声子晶体的带隙进行物理降噪,不同于传统的电子滤波器,物理滤波具有更加高效的滤噪能力,基于声子晶体具有的带隙特性,使得它在降噪和声学器件等方面都有着广阔的应用前景。

本文针对声发射波源的检测概率,提出了一种基于声子晶体滤噪的方式,识别裂缝扩展引发的真实声发射信号,从而直接计算评估声发射波源的检测概率。利用紧凑拉伸试验验证了所提出方法的有效性,通过对比常规铝合金试件(plain plate)和植入声子晶体的植晶铝合金试件(stubbed plate)的声发射活动,利用传统的检测概率计算方式,即真实信号与总信号数的比值来评价声发射波源检测概率。文章也开展了参数研究,分析了裂缝长度、阈值、频率等变化对检测概率的影响。

1 基于声子晶体的物理带隙设计

通过设计和部署声子晶体形成“带隙滤波器”,从而在声发射传感器和可能的噪音源之间形成一个“屏障”,用于阻隔噪音或者其他非裂缝扩展所引起的信号,进而使声发射传感器仅仅采集真实的裂缝信号。通过查阅文献可知,在铝合金材质中,裂缝扩展过程中所伴随产生的声发射信号的频率范围一般在100～200 kHz,其峰值频率通常在150 kHz左右,如果可以通过设计声子晶体形成150 kHz左右的带隙,即可以阻隔由于试件夹具处摩擦而产生的声发射信号,使得传感器仅接收到由于裂缝扩展产生的绝大多数真实声发射信号。本文的声子晶体设计是通过调整部署于试件表面的圆柱体金属的参数(突起的直径、间距和高度)来实现的。设计计算过程在多物理场耦合有限元软件COMSOL5.5中进行,通过参数分析(金属圆柱体直径、高度和间距)来调整频散曲线,直至形成150 kHz带隙为止,最终形成声子晶体的最终设计(晶胞结构)。晶胞结构包含圆柱体突起及与之相接触的底板,如图1所示,基于布洛赫波理论(Bloch theorem)的晶格周期性边界条件应用于晶胞的四个边。开展特征频率分析,即利用扫掠波数(k)找到在不同波数k下结构的特征模式的波矢值,其中波数的扫掠范围为波矢在x和y方向的最高对称点数,即晶胞中的Γ、Χ、Μ。为了形成在150 kHz附近的带隙,圆柱体突起的尺寸将根据该频率进行调整,基板厚度hp为常数3.175 mm,通过不断调整a,hs及d的尺寸来分析试算,最终确定构成晶胞的金属圆柱体直径d为7.2 mm,突起高度hs为9 mm,晶胞尺寸a为9 mm,及圆柱突起的间距(圆柱中心之间的距离)为9 mm。对应的频散曲线及晶胞构造如图2所示,通过频散曲线明显可以看出在150 kHz频率附近形成了约为40 kHz带宽的带隙。

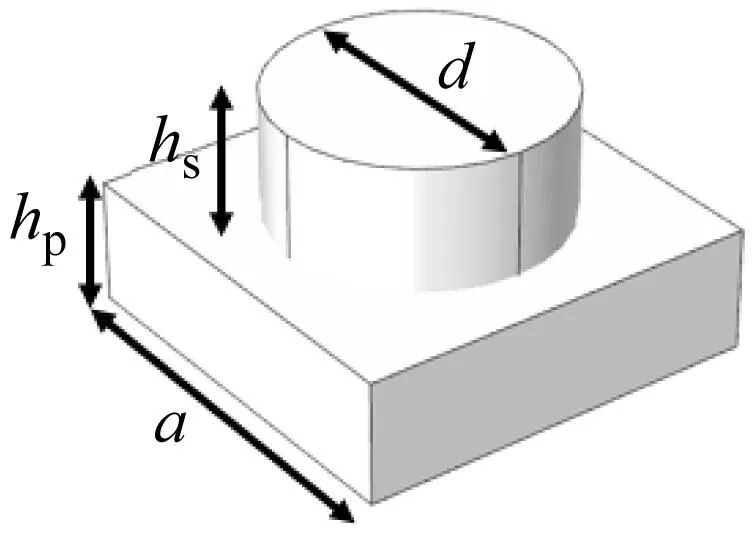
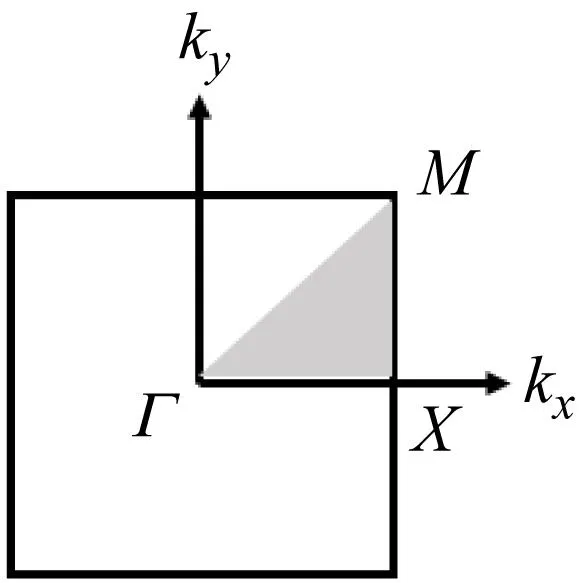
a为晶胞尺寸;d为金属突起直径;hs为金属突起高度;hp为基板厚度。图1 晶胞模型及其对应的第一不可约布里渊区Fig.1 The cell model and its corresponding first irreducible Brillouin zone (IBZ)

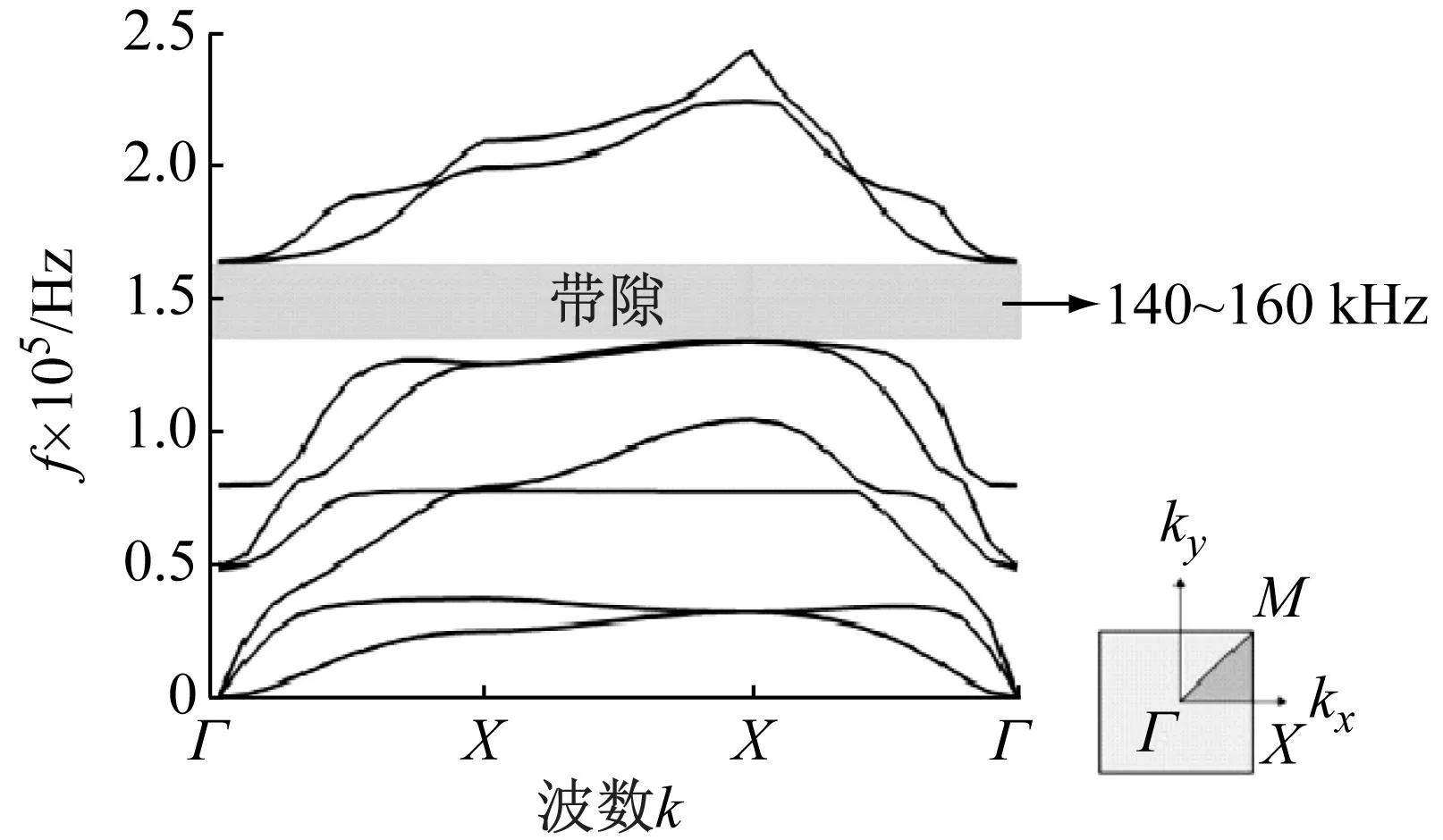
图2 本文设计的声子晶体的频散曲线及其对应的带隙区域Fig.2 The dispersion curve of designed phononic crystals and the corresponding band gap

为了进一步验证带隙的有效性,进行了试验验证,试验中采用固定频率150 kHz猝发音超声波作为已知波源进行激励,采用透射模式(through transmission mode),试验样品采用与紧凑拉伸试验同样材质的铝合金基板,板上部分位置布置设计好的声子晶体,试验设置如图3所示。其中,两次试验保持了激发和接收传感器间距的一致,唯一的变量为是否布置声子晶体。试验结果表明,在同样的激励信号下,未布置声子晶体的一方所接收到的声波信号具有较高的振幅,如图4(a)所示。在布置了声子晶体的一方,超声波传感器所接收到的信号强度明显降低,如图4(b)所示。为了进一步分析比较,截取图中的窗口信号,窗口大小的选择主要是为了尽可能的消除由于试件较小而引起的反射信号所带来的影响,使所分析的波形信号纯粹简单,且尽可能的只包含首波的信息,对所选取的窗口信号并进行快速傅里叶变换,结果如图4(c)所示,明显可以看出两者在150 kHz处的峰值频率所对应的幅值存在差异,未设置声子晶体的信号强度是设置的17倍左右,更进一步证明了声子晶体带隙的有效性。

(a) 具有带隙PC

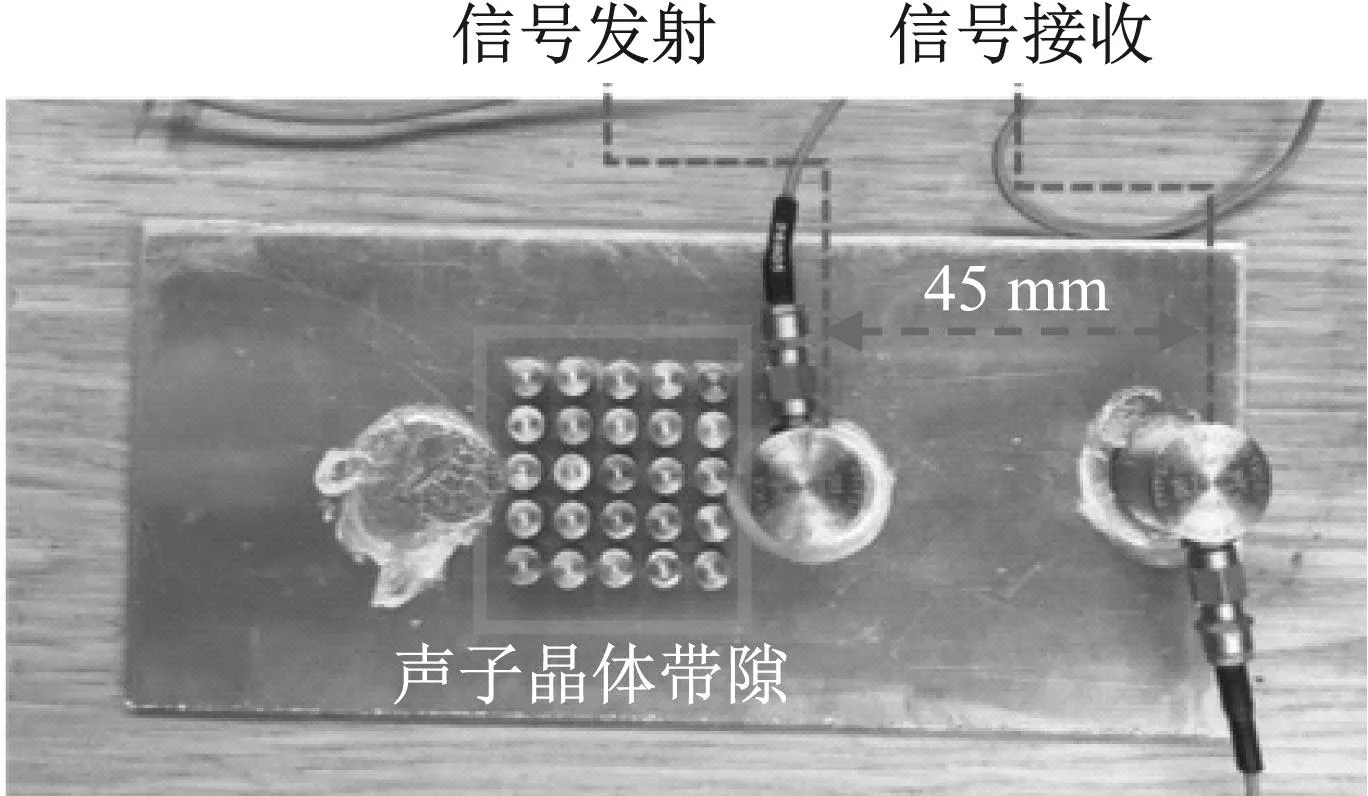
(b) 无带隙PC图3 声子晶体带隙验证试验Fig.3 Test setup for evaluating the performance of phononic crystal band gap

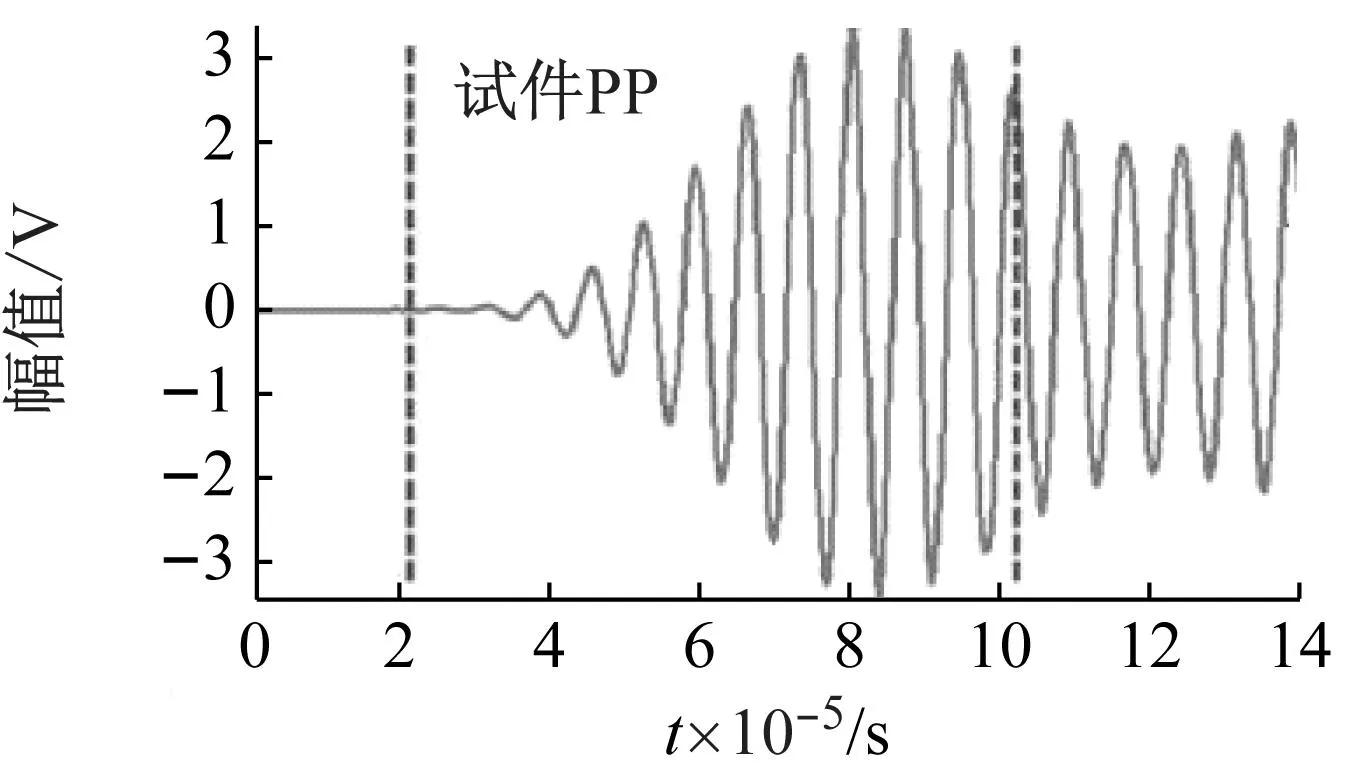
(a) 原始回波信号

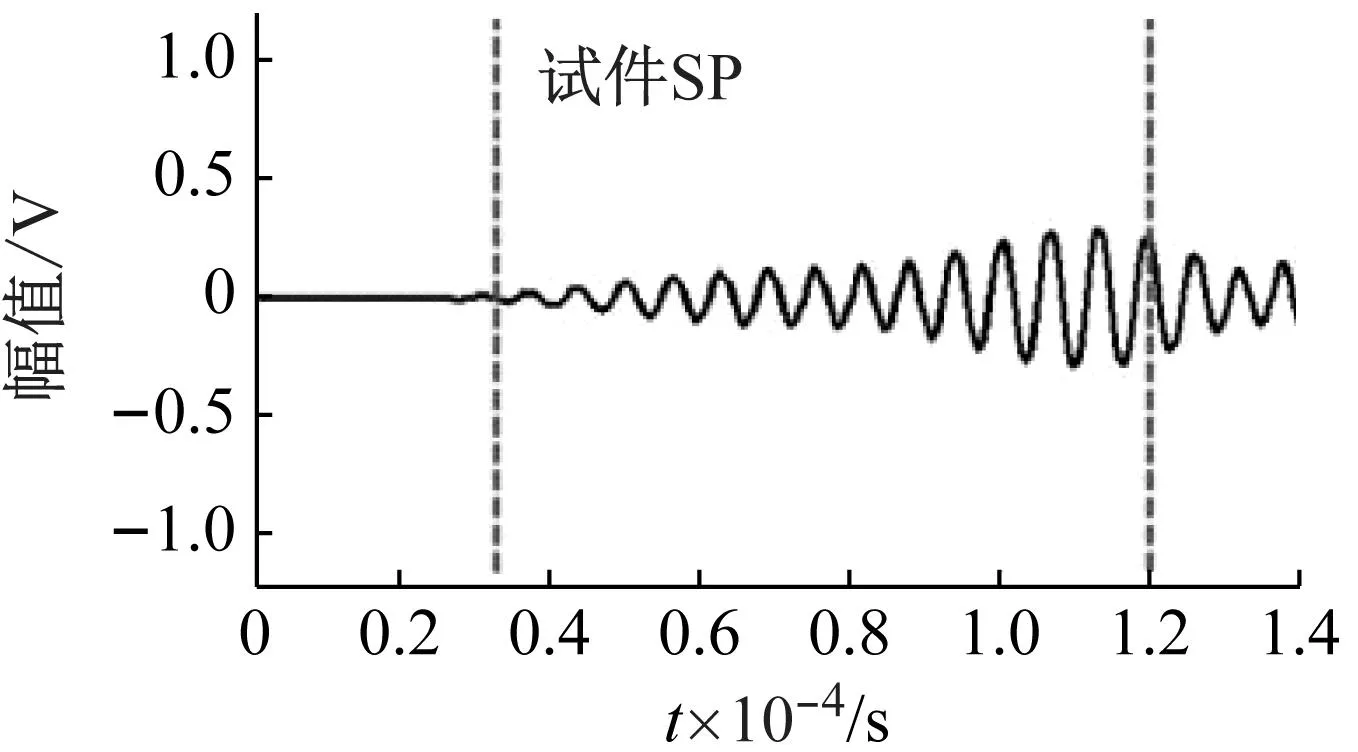
(b) 带隙滤波后的信号

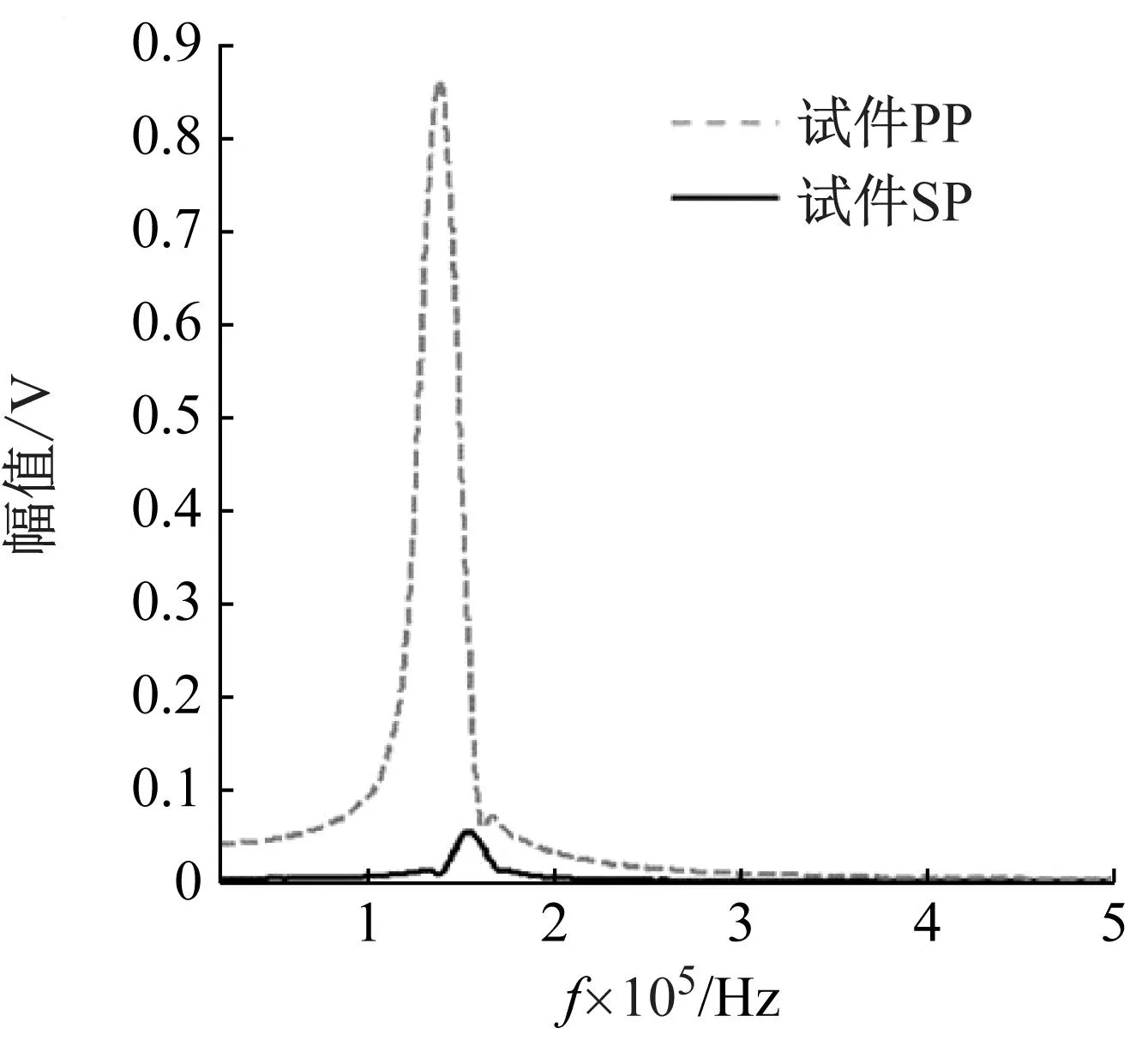
(c) 频域中的幅值图图4 声子晶体带隙效果图Fig.4 The performance of the band gap formed up by the phononic crystals

2 紧凑拉伸试验概况

2.1 试件设计与试验概况

对本文所设计的声子晶体结合紧凑拉伸试验来量化声发射检测中的检测概率。首先进行紧凑拉伸试验的试件设计和制作,参考ASTM E647—2000规范[26],试件具体的尺寸细节如图5(a)所示,材料采用铝合金7075-T6,厚度为3.175 mm,另外在缺口两端距离19.3 mm处设有直径为8 mm的圆形缺口作为夹具锚固点。同样的试件制作2块,其中一块设置声子晶体,构成声子晶体铝合金板试件(stubbed plate, SP),而另外一块为常规铝合金板试件(plain plate, PP),试验试件如图6所示。

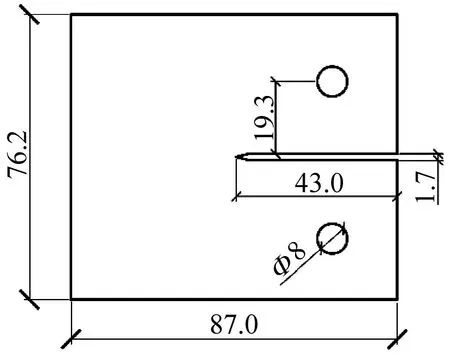
(a) 试件尺寸详图

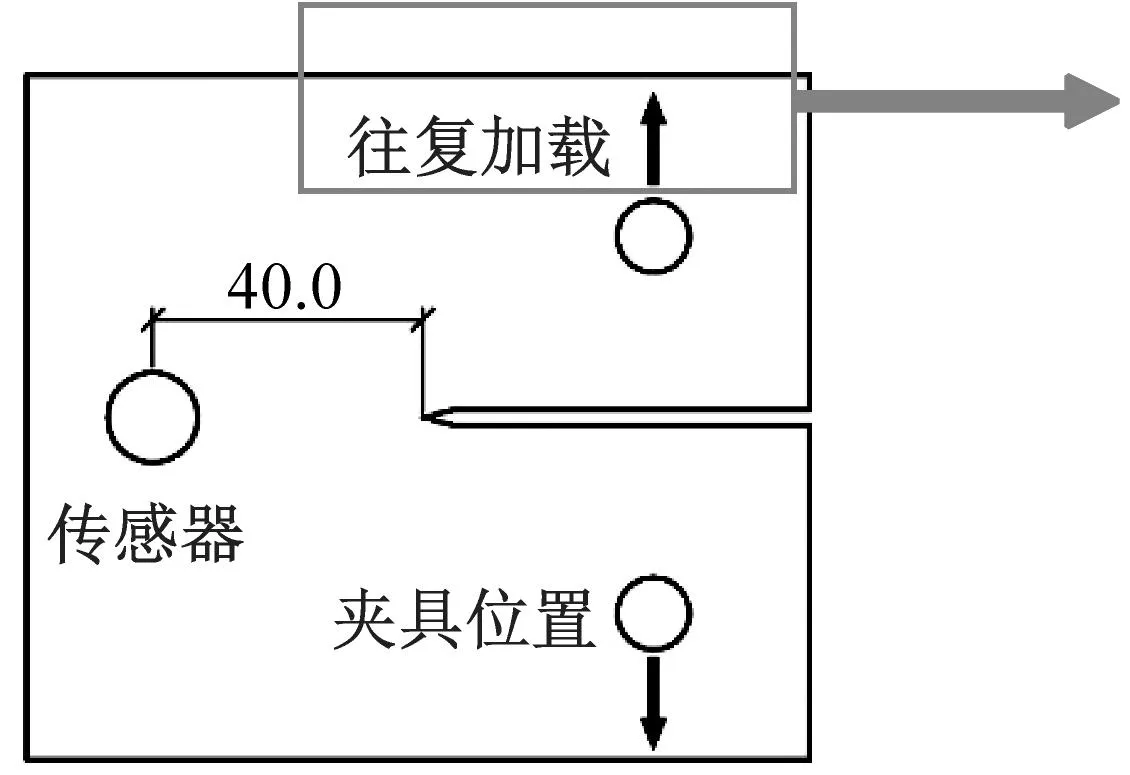
(b) 传感器及加载方式

(a) 试件PP

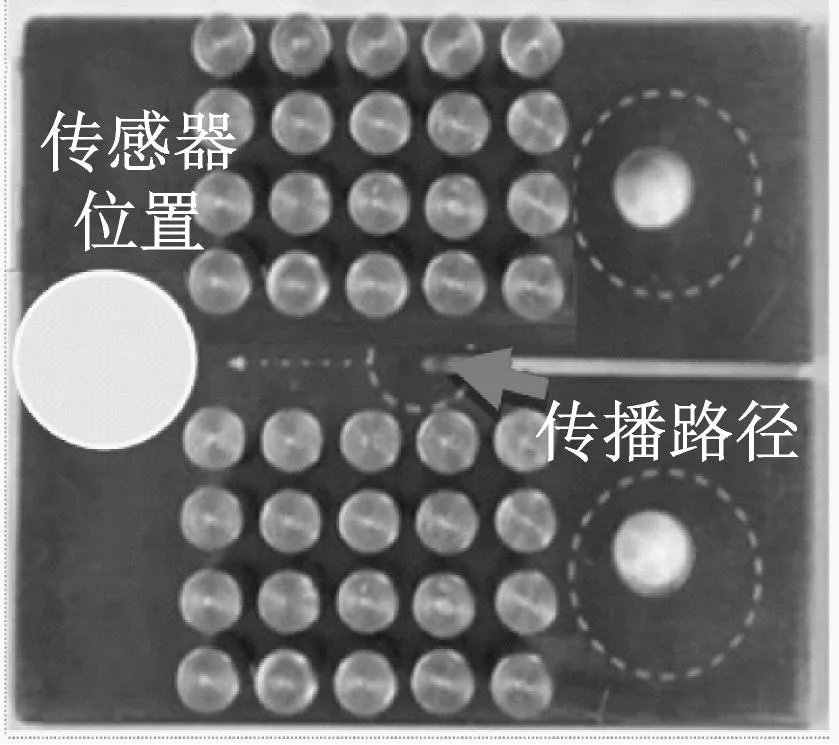
(b) 试件SP图6 试验试件和噪音信号传播图Fig.6 Test specimen and noise signal propagation diagram

紧凑拉伸试验在Instron 8500加载机上进行。其中,加载夹具固定于铝板缺口两端的圆形缺口处,考虑到布置声子晶体及对照试验的一致性,将传感器布置于板中靠左端距离试件切口尖端40 mm处,如图5(b)所示。紧凑拉伸试验利用加载夹具对铝合金板特定位置进行固定,应用拉力-拉力(tension-tension)的加载模式(最大和最小拉力分别为1 500 N和200 N)施加循环速率为2 Hz的正弦应力负载进行试验,试验加载制度如图5(c)所示。声发射数据采用美国物理声学公司的Sensor Highway III信号采集器配合R15传感器(谐振频率150 kHz)进行采集,传感器采用强力胶作为耦合剂。此外其他的声发射系统设置为采集阈值40 dB,将低通滤波器和高通滤波器所有通道的频率分别设置为5 kHz和400 kHz。加载过程中采用40倍光学显微镜全程监测并录像记录裂缝,录像帧率采用60 FPS,试验装置如图7所示。

图7 试验装置Fig.7 Test setup

2.2 基于声子晶体的声发射检测概率试验原理

本试验通过分别对两块试件施加循环加载形成疲劳裂缝,而采用紧凑拉伸试验正是可以控制裂缝沿着预设切口方向扩展,从而更容易识别由于裂缝扩展而产生的声发射信号。本试验在加载过程中将产生大量声发射信号,其原因为两类:一类是裂缝引起的真实声发射信号;另外一类是加载时,夹具处由于摩擦等原因产生的噪音信号。文中所提出的评价检测概率的方法正是通过两块试件的对比试验,计算出声发射波源的检测概率:第一块试验样品为常规铝合金试件(PP),由于没有设置声子晶体进行阻隔,该试件能收集到铝合金板在循环荷载下产生的所有的声发射信号(包括有铝合金真实裂缝引起的信号和循环荷载作用在约束点的摩擦噪音或者其他非裂缝扩展所引起的信号),试件PP及其噪音信号传播如图6(a)所示;第二块则是在常规铝合金试件的基础上,在传感器与摩擦噪音之间设置声子晶体的铝合金试件(SP),该试样上布置的声子晶体能有效地隔绝由于加载时夹具摩擦产生的噪音信号,仅接收来自金属裂缝扩展的真实损伤信号,试件SP及其噪音信号传播如图6(b)所示。为了确保以上所提声发射检测概率的计算方法有效,有以下假设:

(1) 由于本试验所设计的试件尺寸小,故假定波的幅值不会受到传播路径的影响,即没有衰减的影响;

(2) 试验过程中,假设试件SP中所记录的全部声发射信号均为裂缝扩展所产生的真实声发射信号;

(3) 试验过程中,假定试件PP和试件SP的试验条件完全一致,忽略两次试验由于试件安装、传感器布设等引起的差异;

(4) 声发射的绝对能量与裂缝长度成正比。

3 试验结果分析与讨论

3.1 裂缝扩展行为分析

通过在显微镜下对两块试件上的裂缝扩展进行观测,得到两者在整个加载过程中的裂缝扩展历程,如图8(a)所示。两块试件在往复荷载下,开裂时间及裂缝扩展的过程均有所偏差,为便于对比两块试验金属板在裂缝扩展过程中产生的声发射信号,将两块试件的裂缝扩展历程进行归一化处理,通过调整两块试件的裂缝初始扩展时间以及最大裂缝扩展长度,具体来说就是分别利用真实扩展的最大裂缝长度进行归一化处理,使得两块试件的裂缝扩展同步化,结果如图8(b)所示。通过对比两个试件的真实裂缝扩展趋势,将裂缝扩展分为三个阶段:(i) 裂缝萌发阶段,为初始裂缝扩展时起至裂缝宽度为0.68 mm时;(ii) 裂缝稳定扩展阶段,为试件PP的裂缝宽度为0.68 mm～1.9 mm的范围内;(iii) 裂缝快速扩展-破坏阶段,为试件PP的裂缝宽度为1.9 mm～5.43 mm的范围内,如图8(c)所示,对于试件SP,最终裂缝长度为4.19 mm。除阶段(ii)外,两块试样的裂缝扩展为近乎均速的直线扩展,说明声子晶体并没有明显影响铝合金板的裂缝扩展行为。总体而言,整个裂缝扩展时间约为5 000 s,两块试件裂缝扩展过程总体差异不大,仅在阶段(ii)出现短暂差异。

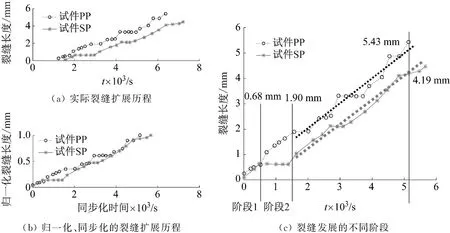
图8 裂缝扩展历程图Fig.8 The progress of crack growth

3.2 基于声发射能量的检测概率

通过对两块试件进行紧凑拉伸试验,在两块试件整个裂缝扩展过程中,分别读取并记录两块试件的声发射的绝对能量值,如图9所示。结果表明,在裂缝扩展行为基本一致的条件下,试验过程中试件SP上的传感器采集到的真实裂缝所产生的声发射信号较少,释放的声发射能量较低,这是由于大量噪音和假信号(fault signal)被布设的声子晶体所屏蔽,相比于试件PP而言,尽管两者间的裂缝扩展过程相似,但试件PP收集的声发射信号所释放的声发射能量达到试件SP的三倍之多,而当裂缝扩展时间为4 000～5 000 s时,两者所释放的声发射能量相差10倍左右,证实了试件PP上的传感器接收到的声发射信号除真实裂缝信号外,还有约束点摩擦噪音或者其他非裂缝扩展所引起的大量声发射信号。

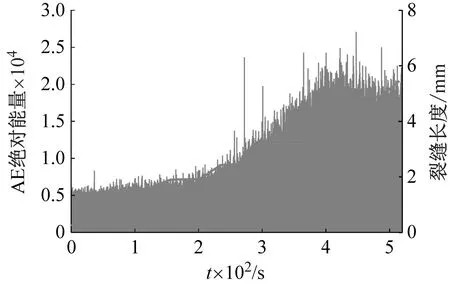
(a) 在试件PP中

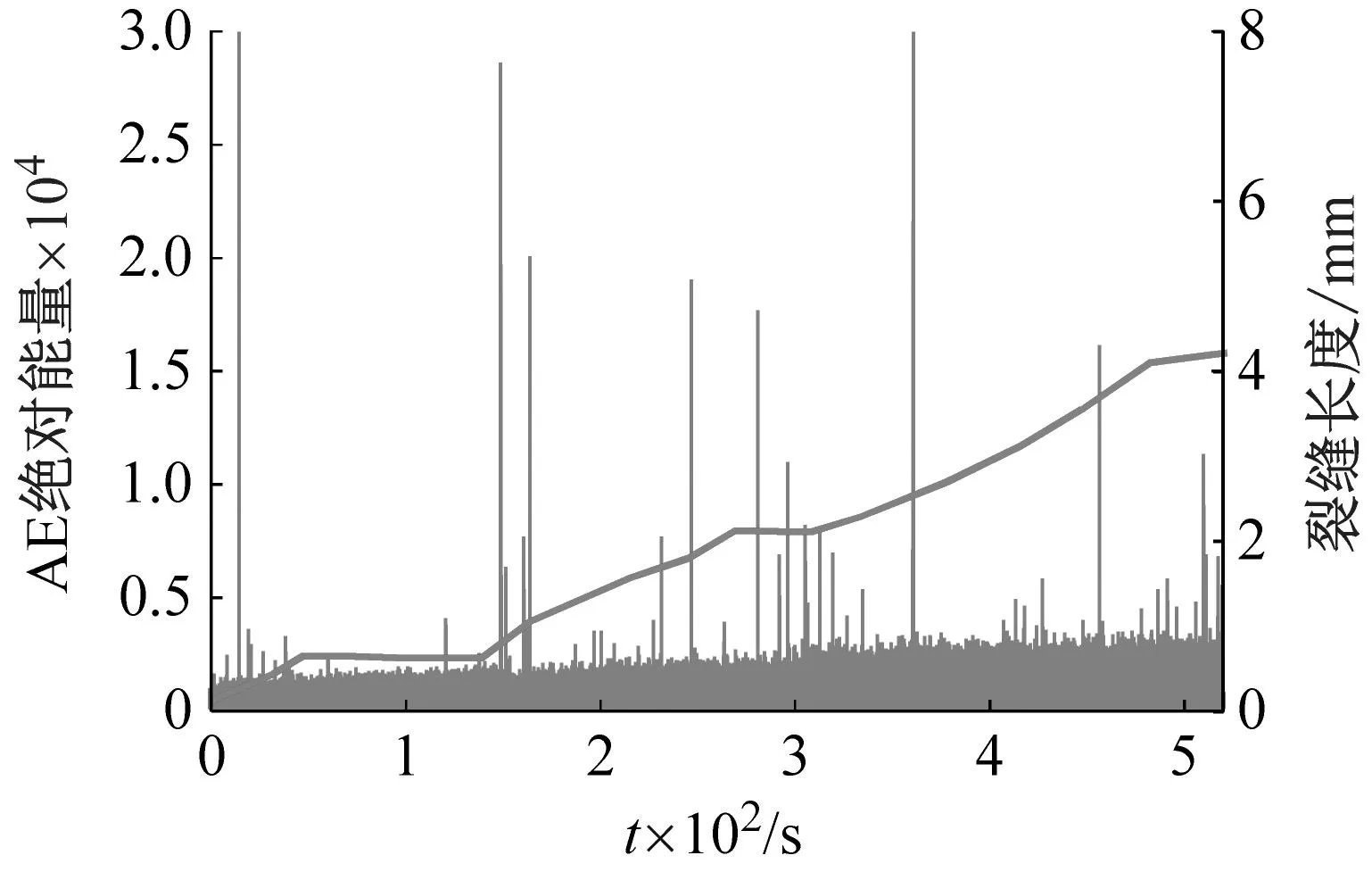
(b) 在试件SP中图9 声发射能量历程图Fig.9 The history diagram of AE energy

通过统计两块试验板的声发射能量,得到了试件SP和试件PP的累计声发射能量历程,如图10所示,此时声发射的检测概率方程如下

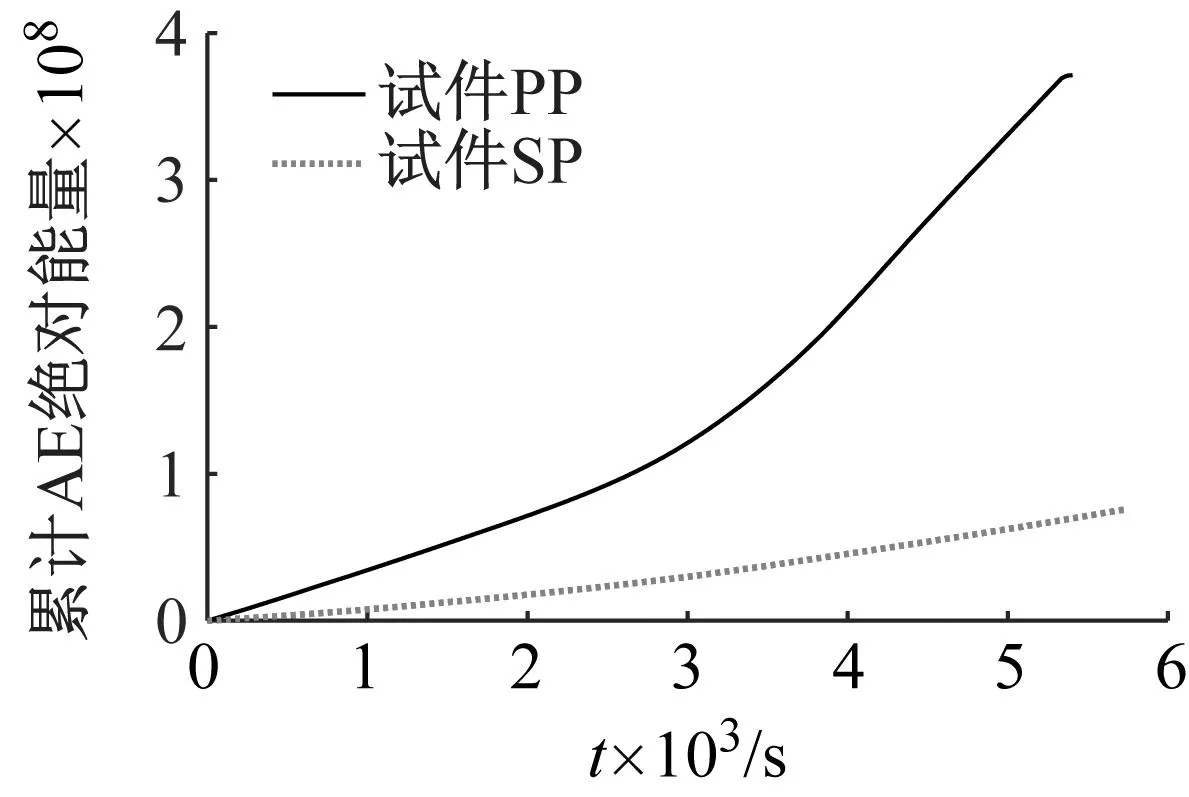
图10 累计声发射能量历程图Fig.10 History diagram of cumulative AE energy

(1)

式中:Ereal1为试件SP的真实裂缝产生的累计声发射能量;Etotal1为试件PP的全部累计声发射能量。

根据检测概率的计算结果,结合裂缝扩展历程图分析,得到检测概率-裂缝扩展的关系图,如图11所示。结果表明,在(i)阶段(裂缝萌发阶段),检测概率变化趋势不明显且数值较低,约为20%。在(ii)阶段(裂缝稳定扩展阶段),检测概率开始迅速提高,在该阶段末,检测概率达到最大,检测概率值达到80%左右。在(iii)阶段(裂缝快速扩展-破坏阶段),检测概率随着裂缝扩展开始缓慢降低,最终下降至20%左右开始趋于平稳。

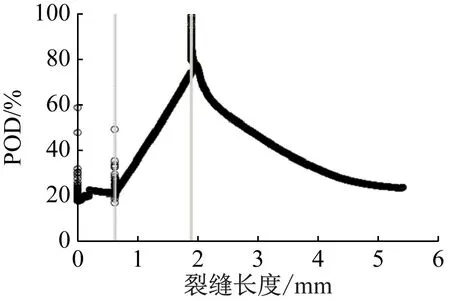
图11 基于声发射能量的检测概率历程图Fig.11 POD process based on AE energy

3.3 基于声发射撞击的检测概率

本节基于声发射撞击的条件下研究裂缝扩展-检测概率的关系,以及阈值和频率对检测概率的影响。经过测试发现,在使用低于45 dB的阈值时,试件PP的撞击数量为10万以上,而试件SP上的撞击数量在700左右,其检测概率较低,说明低于45 dB的阈值不合理,故在基于声发射撞击的检测概率研究中,将阈值下限设置为45 dB。原试验使用的声发射系统的采集阈值设置为40 dB,低通滤波器和高通滤波器所有通道的频率分别设置为5 kHz和400 kHz,通过紧凑拉伸试验得到两块试件在裂纹扩展过程中产生的声发射信号数据。尽管试验的设置尽可能地一致,但裂缝发展为不可控因素,为降低试验误差,故后续试验数据通过对原始试验数据进行后处理得出。

现通过MATLAB对原始的声发射信号数据进行后处理,将振幅低于45 dB的声发射信号移除,得到阈值设置为45 dB的声发射信号数据,其累计的声发射撞击历程,如图12所示。结果表明,在相似的裂缝扩展下,试件SP在裂缝扩展时间为5 000 s时的累计声发射撞击有661次,而试件PP的累计声发射撞击有60 115次,结果再次证实了在紧凑拉伸试验下,试件PP上产生除真实裂缝的声发射信号外,还有其他非裂缝发生引起的声发射信号。

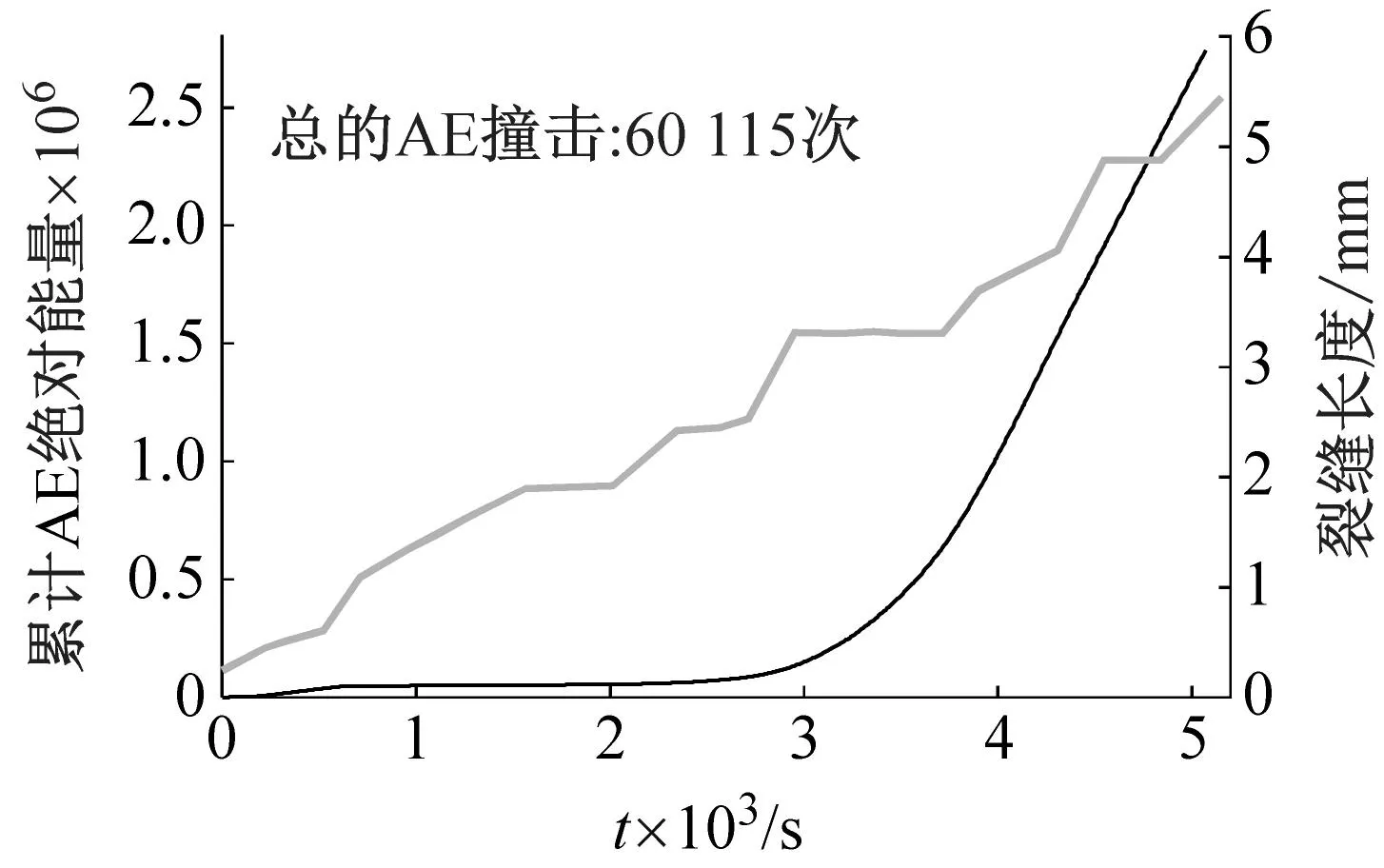
(a) 在试件PP中

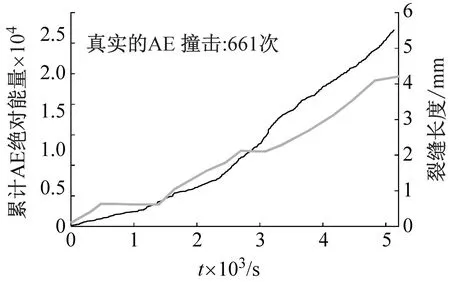
(b) 在试件SP中图12 累计声发射撞击历程图Fig.12 History diagram of cumulative AE hits

为了对比不同设置阈值和频率下的声发射检测概率,同样的,通过MATLAB对所采集的声发射信号进行后处理,得到不同的阈值和频率范围下的声发射信号数据,将各条件下的声发射信号数据进行计算,统计得到对应的累计声发射撞击历程,汇总各条件下的累计声发射撞击总数,结果如表1所示。此时,对应的基于声发射撞击的检测概率方程如下

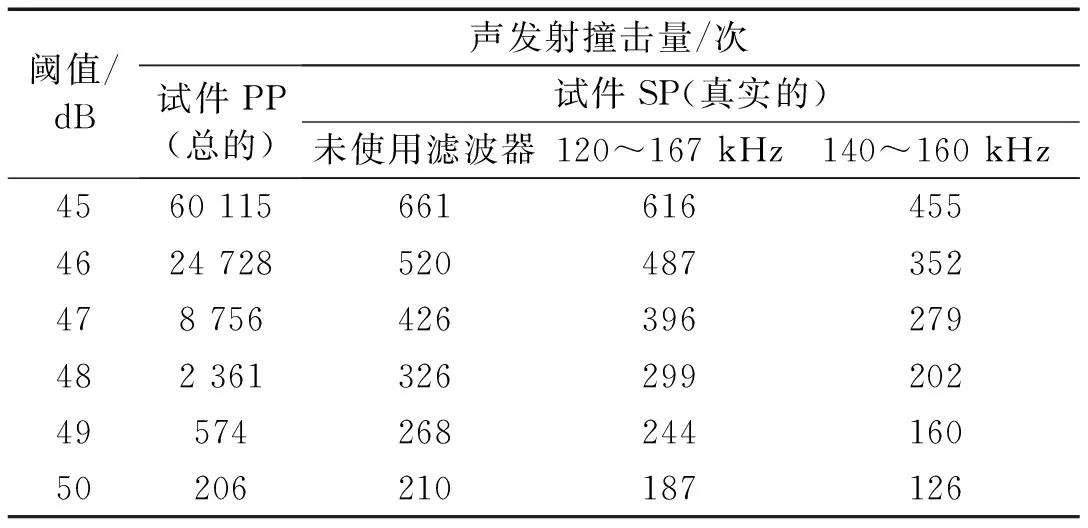
表1 基于阈值和带通滤波器频率控制的累计声发射撞击统计Tab.1 The statistics of cumulative AE hits depending on the threshold and bandpass filter in the AE system

(2)

式中:Ereal2为试件SP上采集到的真实裂缝累计声发射撞击;Etotal2为试件PP上采集到的全部累计声发射撞击。

结果表明,在相同的频率下,随着阈值的提高,两块试件上的累计声发射撞击总数下降,说明设置阈值能有效地过滤掉部分非裂缝扩展产生的声发射撞击,当阈值设置为50 dB,声发射检测概率的计算结果出现错误,此时试件SP接收的裂纹信号撞击比试件PP接收到的总信号撞击多,说明此时出现部分真实裂纹信号被移除的情况。另外的,随着频率范围的调整也能

有效地过滤部分非裂缝扩展产生的声发射撞击,且不同频率范围的过滤效果也有所不同,故通过使用适当的滤波器能使得到的声发射检测概率更加可靠。

基于两块试件在各条件下的累计声发射撞击历程,运用式(2)对每一个时刻的裂缝长度和与之对应的累积撞击数进行统计计算,分别统计出在各个条件下基于累计声发射撞击的检测概率与裂缝扩展的关系图,以频率为变量进行汇总,结果如图13所示。

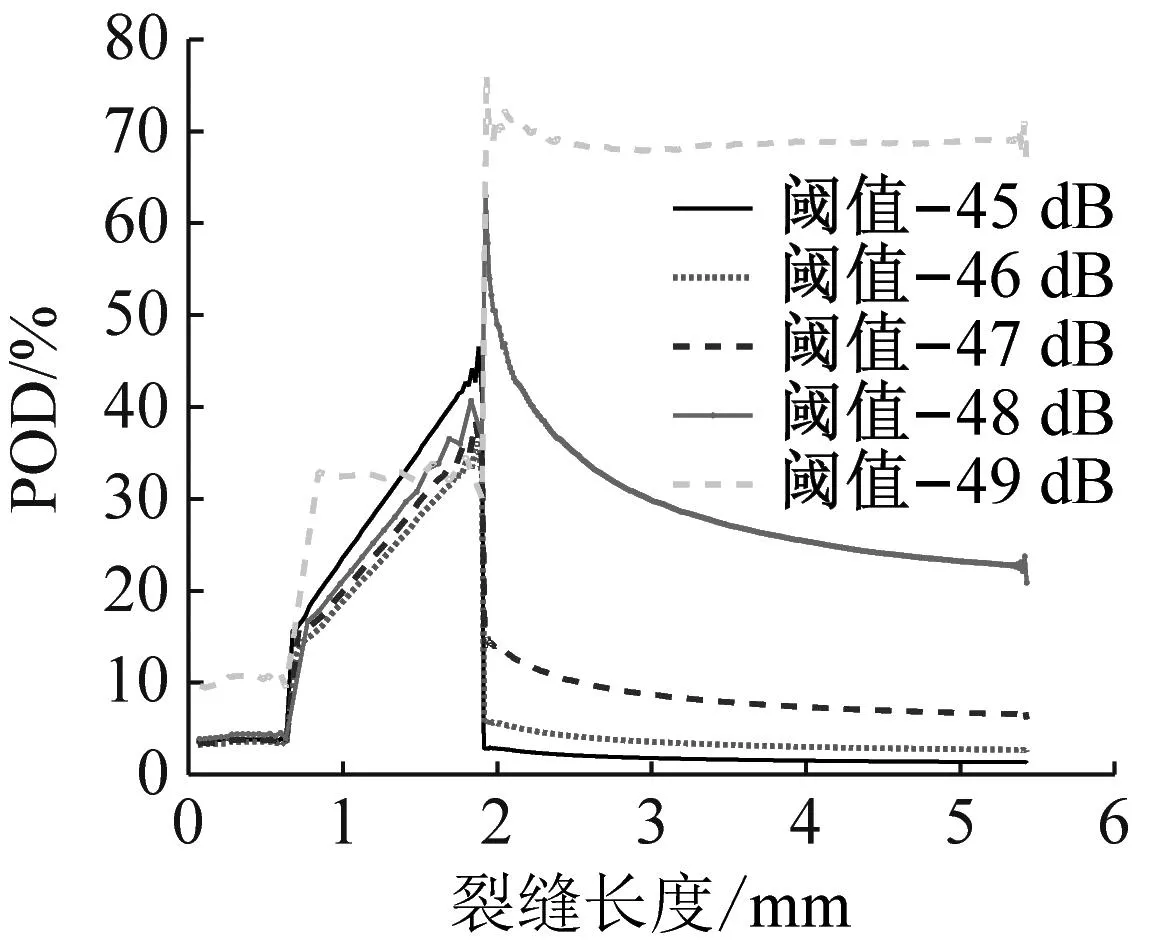
(a) 仅基于撞击

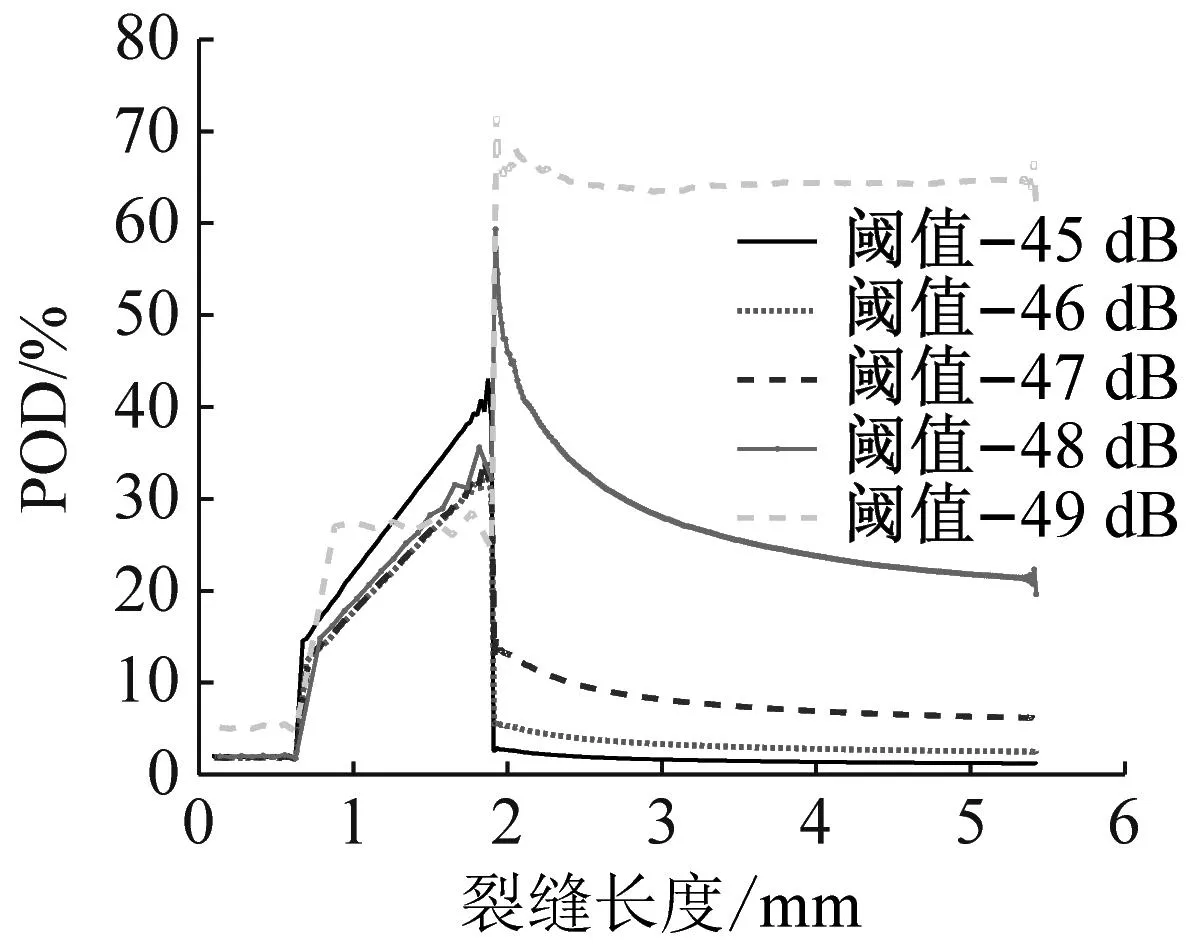
(b) 撞击+带通滤波器(120～167 kHz)

结果表明,基于累计声发射撞击的检测概率变化曲线与基于声发射能量的检测概率变化曲线相似。另外,随着阈值设置的提高,能有效阻隔大部分非裂缝的声发射信号,减少非裂纹扩展产生的声发射撞击,使得检测概率得到有效的提高,当阈值设置为49 dB时,声发射检测概率在整个裂缝扩展中均有较大提高,并在裂缝扩展的(iii)阶段末仍然保持有较高的检测概率值。对比同一阈值设置下的不同接收频率的检测概率曲线,由于限制接收的频率范围,同样也能阻隔部分非裂缝信号,使得最终获得的检测概率更为可靠。

4 结 论

声子晶体是弹性常数在空间呈周期性排列的人工晶体,该材料具有弹性波带隙的周期性结构功能,能在一定频率范围(带隙)内阻碍弹性波传播。本文基于声子晶体的带隙特性,提出一种声发射波源的检测概率研究,利用紧凑拉伸试验验证所提出的声发射波源检测概率的有效性。为此分别设计了一个常规铝合金紧凑拉伸试件(采集总的声发射信号)和一块部署了声子晶体的铝合金紧凑拉伸试件(采集真实裂缝活动的声发射信号)作为对照试件进行试验。两块试件的全部试验工况相同,试验通过观察裂纹扩展并采集沿预设切口方向的裂缝扩展引起的大量声发射信号,以此来分析得到真实波源的检测概率并确定裂缝扩展-检测概率的关系,在此基础上进一步通过设置阈值和带通滤波器来分析阈值和频率对检测概率的影响,结论如下:

(1) 声发射波源检测概率会随着裂缝扩展而提高,当裂缝扩展到一定值时,检测概率开始缓慢降低到一定值后趋于稳定。

(2) 可以通过设置合理阈值从而提高波源检测概率,尽管随着阈值的增大,检测概率也会提高,但是当阈值调高到一定值时则可能会大量移出真实信号,从而导致检测概率结果无法计算。

(3) 使用适当的滤波器能有效阻隔非裂缝扩展信号的影响,从而使得到的检测概率更加的可靠。

本文试验仅基于加载时产生的摩擦噪音影响下的声发射检测概率研究,另外仍然可能存在众多影响结果的其它波源,未来仍需要进行更多的试验样品来证实本文试验的结果。此后还可以将基于噪音源响应的声发射检测概率试验与基于衰减影响的检测概率试验结合,得到更加可靠的声发射检测概率。