基于车桥耦合理论的斜拉桥拉索动力冲击系数及影响因素分析

李子超, 黎剑安, 冯东明

(1.东南大学 混凝土与预应力混凝土结构教育部重点实验室,南京 210096; 2.东南大学 土木工程学院,南京 211189; 3.东南大学 智慧建造与运维国家地方联合工程研究中心,南京 211189)

作为桥梁设计时需要考虑的最主要活载之一,车辆荷载是影响桥梁结构的使用与安全的重要因素[1-4]。车辆通过桥梁时会引起振动,这种振动可能会导致桥梁的最大动态响应明显大于最大静态响应[5],进而给桥梁的安全运营带来威胁。因此,车辆荷载对桥梁的影响是不可忽视的,需要在桥梁设计中充分考虑。然而,车辆和桥梁之间的动力学分析是一个复杂的耦合问题,在桥梁设计时通常引入动力冲击系数,以简化车辆荷载对桥梁动力响应的放大效应[6]。在我国的《公路桥涵设计通用规范》中,通过桥梁基频计算冲击系数[7]。然而,大量研究表明,动力冲击系数还会受到车速、路面不平度、车辆加载位置、车辆数和车轴数等多种因素影响[8]。

斜拉桥交通量大,负载高,服役年限长,对于其在车辆荷载作用下的动力响应研究不容忽略。而拉索作为斜拉桥的重要构件,具有轻质、高柔、低阻尼的特点,在车辆过桥的激励下发生振动,使拉索产生应力变化[9]。拉索长期受到这种应力的加载,极易在锚头处发生疲劳破坏[10],尤其是在复杂的气候和环境条件下,如高温、高湿度和海洋环境,索锚接合处的疲劳损伤风险更高[11]。因此,研究车辆荷载对桥梁产生的动力放大效应对于确保桥梁长期安全运营至关重要。Li等[12]研究了路面不平度对拉索疲劳寿命的影响,发现斜拉索的疲劳寿命随着路面的恶化而降低。此外,路面不平度与桥梁的冲击系数具有较大的相关性,研究拉索冲击系数对于拉索的疲劳研究具有重要意义。Jiang等[13-14]在进行拉索疲劳分析时,采用了动力放大;系数来考虑车辆荷载对拉索应力的放大效应,但是缺乏相关规范与参考作为支撑。

然而,目前对于斜拉桥拉索动力冲击系数的研究相对较少,大部分研究仍集中在斜拉桥的主梁上。肖亚辉等[15]研究斜拉桥主梁的动力冲击系数发现最大动力冲击系数大于规范取值,因此需要对动力冲击系数进行分析。王贵春等[16]研究某双塔双索面斜拉桥,总结了动力冲击系数受路面等级、车速、车重和偏载距离的影响规律。付志方等[17]通过跑车和跳车试验计算出动力冲击系数,发现跳车试验的计算结果远超规范设计。谢旭等[18]发现斜拉桥的动力系数具有较大的离散性,拉索和主梁之间存在明显差异。张为民[19]以苏通大桥为研究对象,发现拉索的冲击系数与长度成反比,且短拉索受车速影响较为明显。而戈伟研究多塔斜拉桥部分拉索的动力响应发现,拉索的动力冲击系数与拉索的应力响应成正相关。李永乐等[20]针对国内某现役的铁路桥在不同的列车编组、车型、行车方向与轨道不平度等因素影响下进行了冲击系数的分析,发现冲击系数在拉索与主梁处受轨道不平顺的影响要大于支座处的影响,但对于公路斜拉桥拉索动力冲击系数的研究缺乏参考价值。研究拉索的动力冲击系数具有以下重要意义:一方面,可以快速、有效地估计车辆移动时的拉索应力;另一方面,分析拉索动力冲击系数以及其分布情况,可以发现斜拉桥拉索在车辆动荷载作用下的薄弱位置,从而提高拉索的承载能力评估等方面的精度和可靠性。

由于拉索动力冲击系数是评估拉索所受车辆荷载的关键指标,然而目前对斜拉桥拉索动力冲击系数的研究相对较少。本研究选取一座典型的斜拉桥和五轴重车为研究对象,研究了不同工况下的拉索动力冲击系数。数值案例分别探讨车辆横向位置、路面不平度、车辆行驶速度等因素对拉索动力冲击系数的影响。提出了拉索动力冲击系数的建议取值,为公路斜拉桥拉索动力冲击系数的相关研究提供了参考和依据。

1 拉索动力冲击系数

拉索在静态和动态荷载作用下的应力时程如图1所示。在静载作用下,拉索产生的最大应力σs处在对应的动载作用下产生的最大应力为σd。因此,参考动力冲击系数的定义,给出拉索动力冲击系数的定义,即:

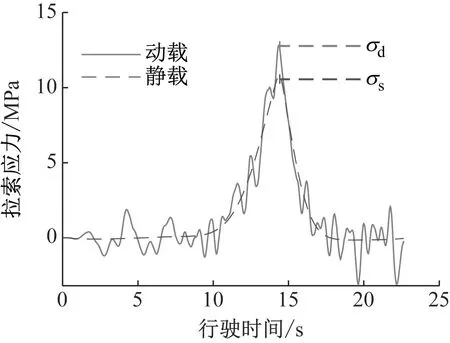
图1 拉索动力冲击系数计算图示Fig.1 Calculation diagram of dynamic impact coefficient of cable

拉索的动力冲击系数(IMσ)指斜拉桥在车辆移动时,桥梁拉索在移动荷载作用下产生的最大应力与静荷载作用下最大应力的增量与最大静响应的比值,其定义式为

(1)

式中:σd为移动荷载作用下拉索的最大应力;σs为车辆荷载作用下拉索的最大静应力。两者在计算动力冲击系数时都需要减去初始索力。

2 车桥耦合模型

2.1 路面不平度

路面不平度是影响车辆与桥梁动力响应的重要因素。在GB/T 7031—2005《机械振动 道路路面谱测量数据报告》[21]中,根据路面的实际情况,对路面不平度进行分级。其中位移功率谱的建议表达式见式(2)

(2)

式中:Gd(n0)为路面不平度系数;n0=0.1 m-1为参考空间的频率;n为空间频率;w为频率指数。

模拟路面不平度的谐波叠加公式如下

(3)

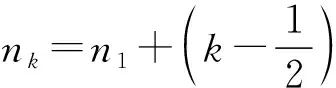
路面等级共可划分为8种[22],当路面等级达到D级时,路面的最大起伏程度可以达到0.1 m,此时路面情况已经比较恶劣,而大跨桥梁路面养护相对比较及时,一般不会出现D级路面情况,因此本文研究取用S、A、B、C四个路面等级。模拟生成的A级路面不平度如图2所示。

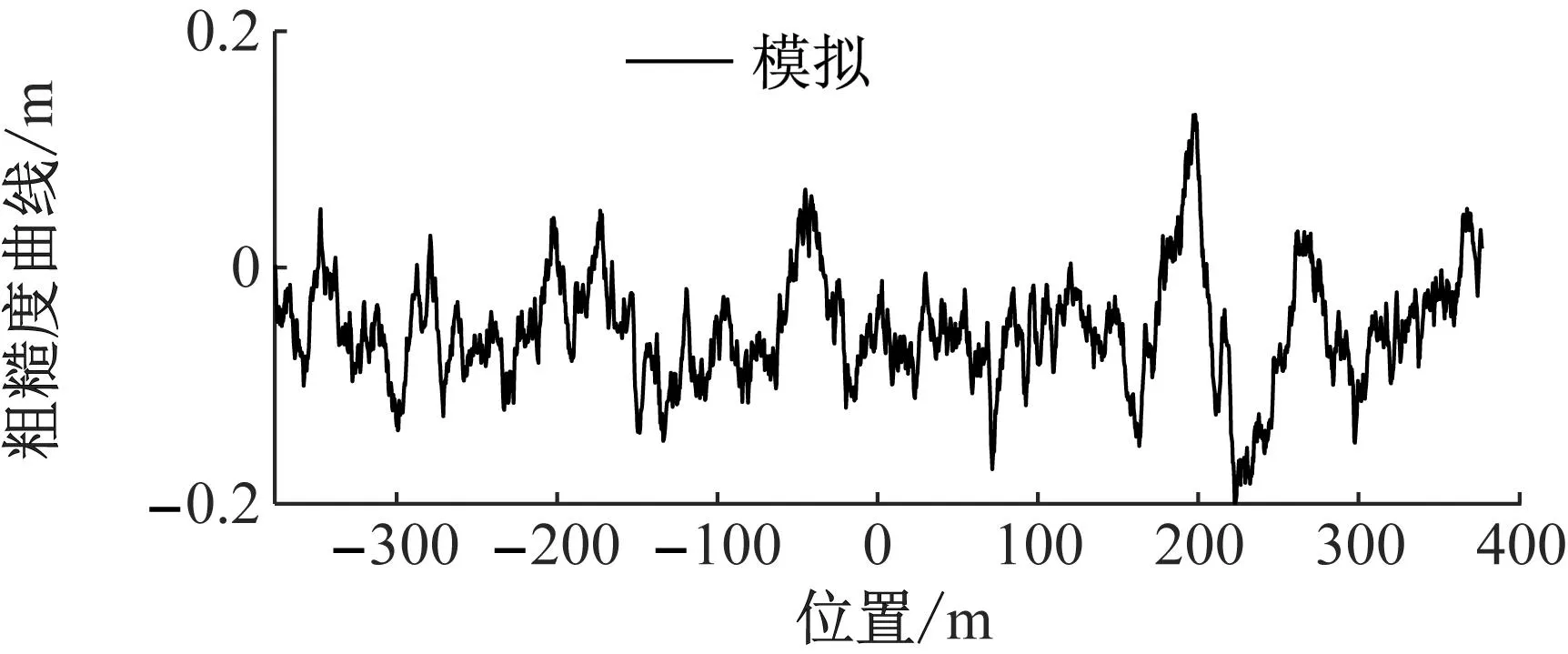
(a) 空间域谱

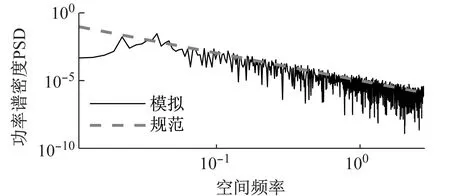
(b) 频域图2 模拟A级路面不平度Fig.2 Simulation of road roughness of Class A

2.2 车桥耦合模型

选取国内某双塔三跨式斜拉桥,桥梁主跨径为756.8 m,主梁采用宽度为37.4 m的扁平钢箱梁,桥面为双向六车道,斜拉索采用斜向双索面,索面形状为扇形。拉索编号如图3所示,上游方向边跨拉索编号为1～13,上游方向主跨拉索编号为14～26,下游方向主跨拉索编号为27～39,下游方向边跨拉索编号为40～52。

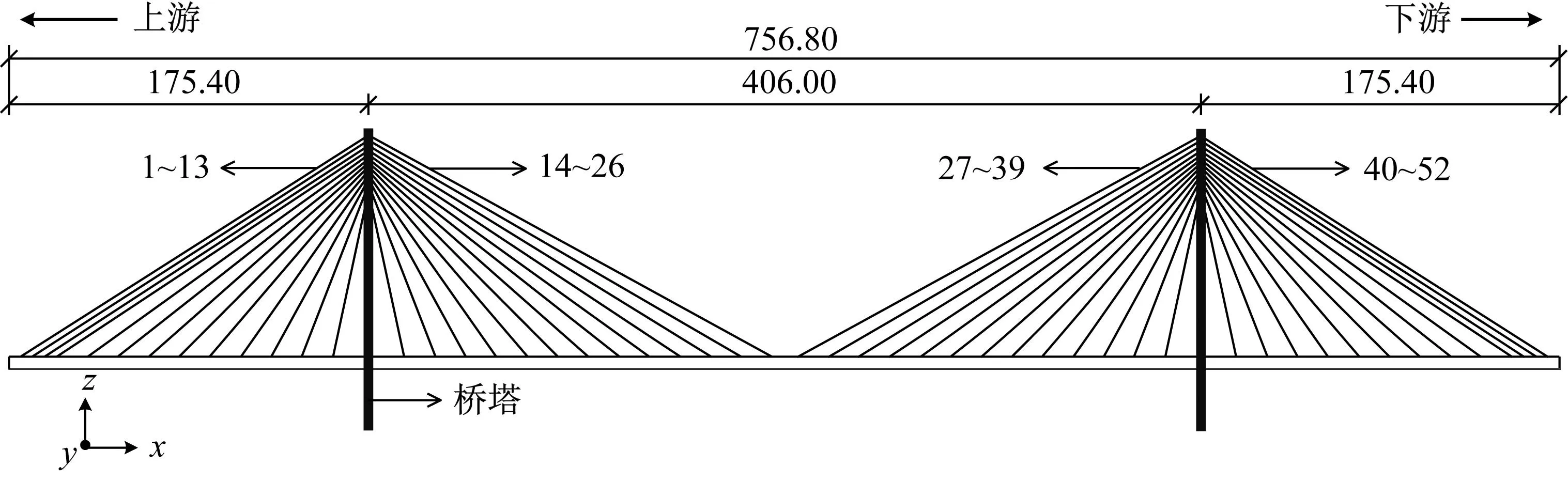
(a) 斜拉桥侧视图

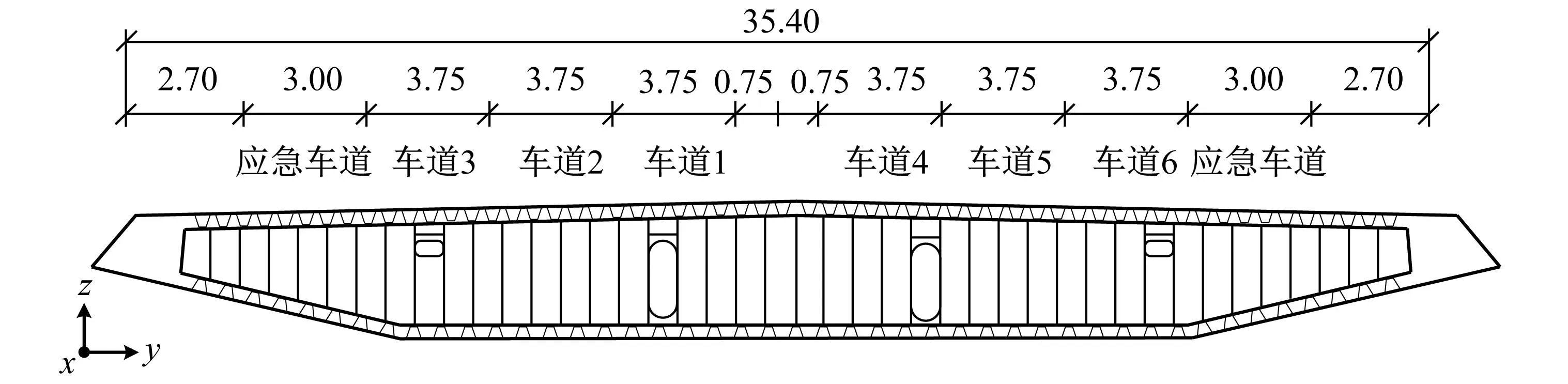
(b) 斜拉桥主梁横断面图图3 斜拉桥总览(m)Fig.3 Overview of cable-stayed bridges (m)

在ANSYS中,钢箱梁采用SHELL63单元建立,斜拉索使用LINK10单元,桥塔使用BEAM4单元,建立了该双塔三跨斜拉桥的壳单元模型。对建立的斜拉桥的有限元模型进行模态分析,表1为计算得到的桥梁前8阶自振频率与振型特征。

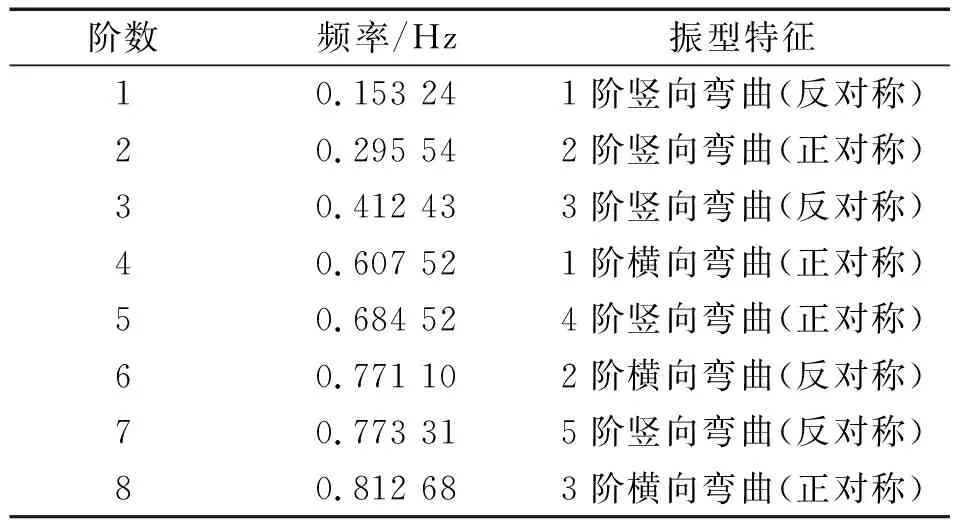
表1 桥梁的自振频率和振型特征Tab.1 Frequencies and modal shapes of modes of the bridge

2.3 车辆模型建立

公路上车辆可根据车轴数、质量、轴距等多种因素分类,从而将车辆简化为质量—弹簧—阻尼模型时会对应不同的参数。为了考虑重载车辆通过桥梁时产生的动力响应,并根据我国JTG D60—2015《公路桥涵设计通用规范》,选取有代表性的总重为550 kN的标准5轴卡车作为研究对象。

邓露等[23]根据规范的车辆荷载,通过静力等效与力矩平衡,计算并拟定了5轴车模型的相关参数,并根据调查统计数据与相关的文献研究,确定了规范5轴车车辆模型的刚度和阻尼取值。图4展示了我国设计规范中的5轴车三维车辆模型,车辆设计参数如表2所示。车辆模型单元类型及选项设置如表3所示。

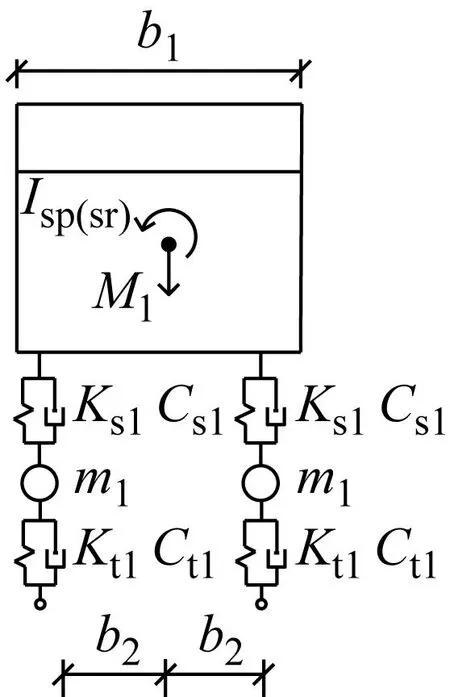
(b) 正视图图4 我国桥梁规范中5轴车三维模型Fig.4 3D model of 5-axle vehicle in China’s bridge specifications

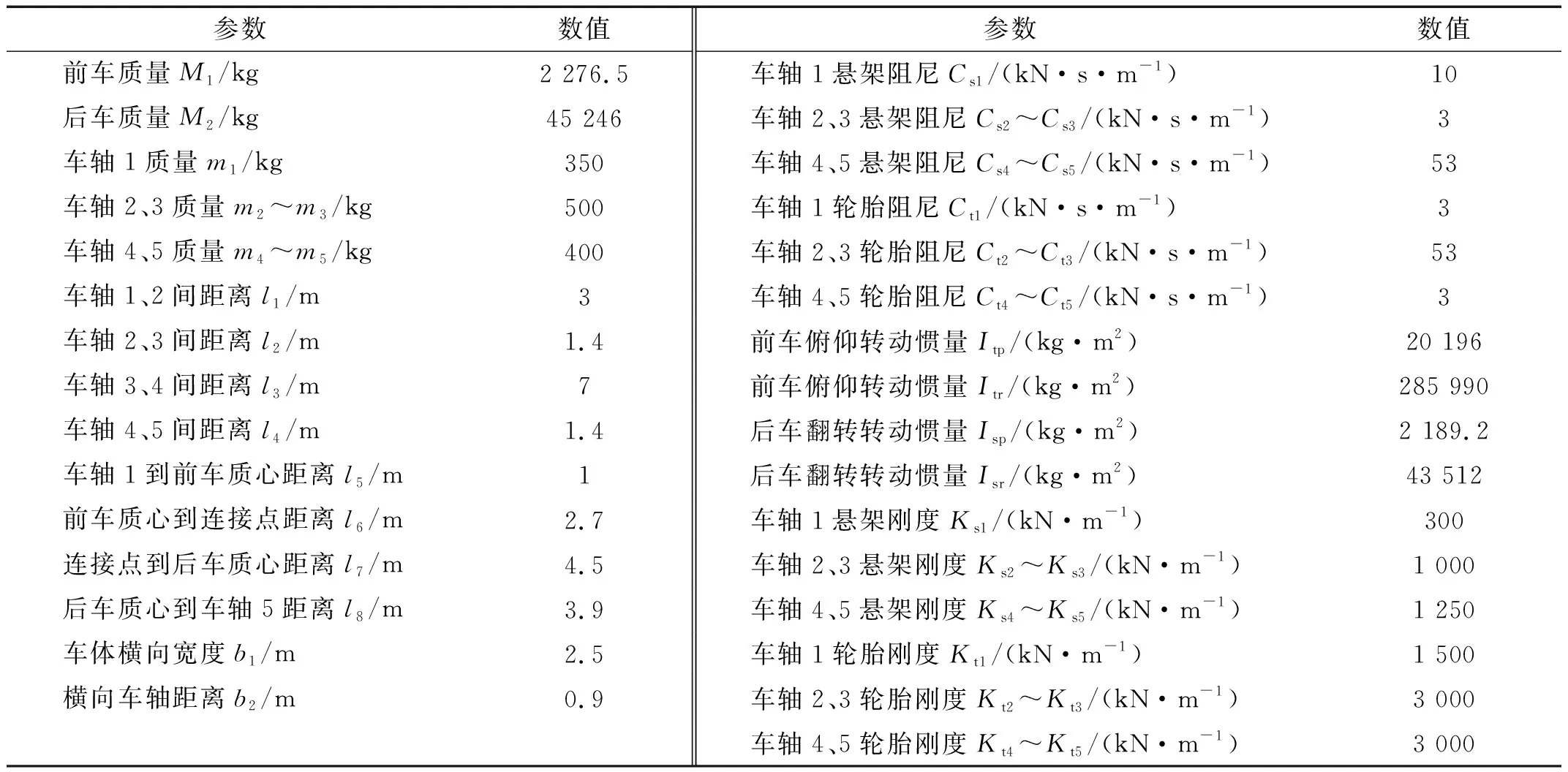
表2 5轴车车辆模型参数Tab.2 5-axle vehicle model parameters

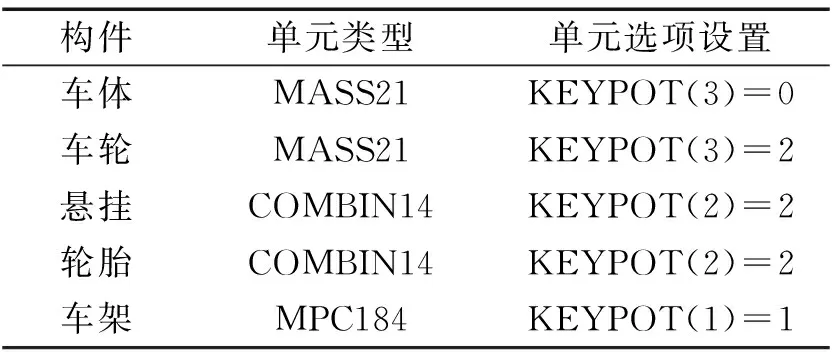
表3 车辆模型单元类型及选项设置Tab.3 Vehicle model unit type and option settings

基于ANSYS中已有的单元建立了该车的有限元模型,采用的单元类型与单元选项设置如表3所示。

2.4 车桥耦合实现

车在桥上行驶时,会引起桥梁发生振动,从而引发桥梁产生动力响应,同时桥梁的振动也会对行驶的车辆施加一个反作用,两者之间相互影响,形成了耦合振动。对于车桥耦合振动的研究需要满足下列四项假定:①车辆考虑了竖向,俯仰以及侧滚自由度;②轮胎与桥面始终紧密接触,不发生分离;③车身为刚体;④结构满足小变形要求[24]。车桥相互作用中,车辆的运动方程可以如下

(4)

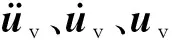
桥梁的运动方程如下

(5)

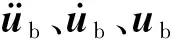
车辆在桥梁上行驶时,桥梁在与车轮的接触点处的位移会对车辆产生动力响应,从而导致车辆受力产生位移。为了保证车辆在桥面行驶的过程中,车辆与路面不发生分离,需要通过建立平衡方程以及位移协调方程来维持上述条件。

平衡方程如下所示

Fvg+Fvb=Fbv

(6)

位移协调方程如下所示

UYv-UYb=r(x)

(7)

式中:UYv为车辆在接触点处的竖向位移;UYb为桥梁在接触点处的竖向位移;r(x)为路面不平度,可以由式(3)计算得到。

为了在有限元计算中满足上述(4)、(5)、(6)三个方程,使用CONTA175接触单元与TARGE170目标单元,建立并模拟车辆与桥梁之间的接触,实现车辆与桥梁之间的耦合。然而,由于使用接触对进行计算时,没有考虑到路面不平度的影响,因此在使用接触对满足耦合条件的过程中,需要通过命令流构建额外的方程,考虑路面不平度的影响,即需要满足方程(7),在ANSYS中的APDL命令如下

CE,NEXT,r,nv,UY,1,nb,UY,-1

(8)

式中:nv为车轮的单元编号;nb为桥梁接触单元编号。

以上为ANSYS中考虑路面不平度的车桥耦合设置,其具体流程如图5所示。

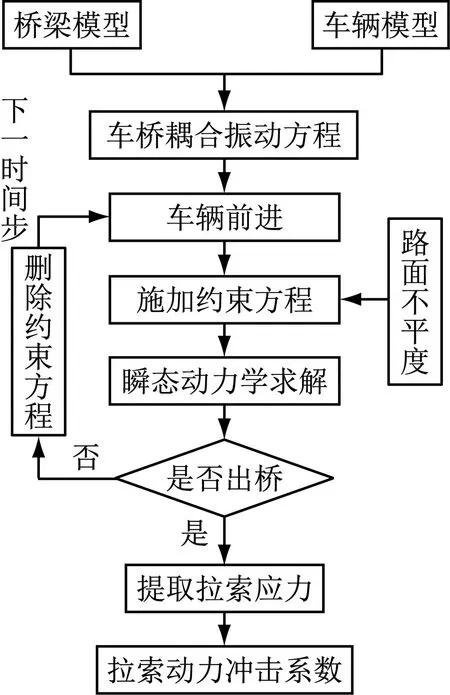
图5 拉索动力冲击系数计算流程Fig.5 Calculation process of cable dynamic impact coefficient

3 数值仿真

3.1 工况介绍

本文主要考虑了路面等级、车道位置、车速三个因素对拉索动力冲击系数的影响,并进行了数值分析,各个影响因素的取值如表4所示。值得注意的是,由于桥型以及荷载施加方式的对称性,在研究单辆车行驶对于拉索动力放大的影响时,仅考虑了车辆单向行驶时的结果与规律。在ANSYS中建立有限元模型并进行车桥耦合分析,提取各种工况下的拉索应力时程并计算动力冲击系数。在表4中,S级即为光滑路面。

表4 计算工况Tab.4 Calculated operating conditions

3.2 仿真结果

根据公路桥涵设计通用规范,冲击系数的计算公式如下

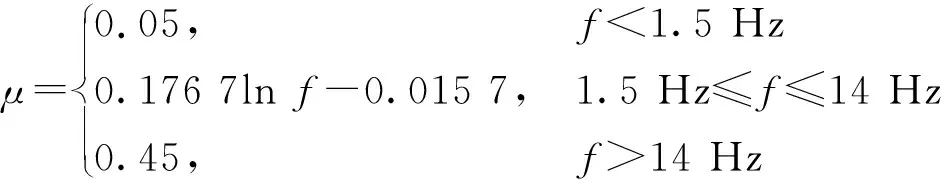
(9)

式中,f为结构基频。

根据式(9)可知,国家规范给定的冲击系数最小值为0.05,最大值为0.45。而本斜拉桥计算出的桥梁自振频率见表1,桥梁1阶振动频率为0.153 Hz,按照规范设计时动力冲击系数应取0.05。

根据式(1)与有限元计算结果,得到所有工况下每根拉索的动力冲击系数,并进行以下分析。

3.2.1 车速的影响

车辆以不同速度行驶在斜拉桥上时,对于桥梁产生的动力响应是不同的,因而对于拉索索力的影响也不相同。将车辆行驶在上行侧时的指定工况下的拉索的动力冲击系数进行汇总,绘制出单侧拉索受到速度变化的动力冲击系数柱状图,如图6所示。

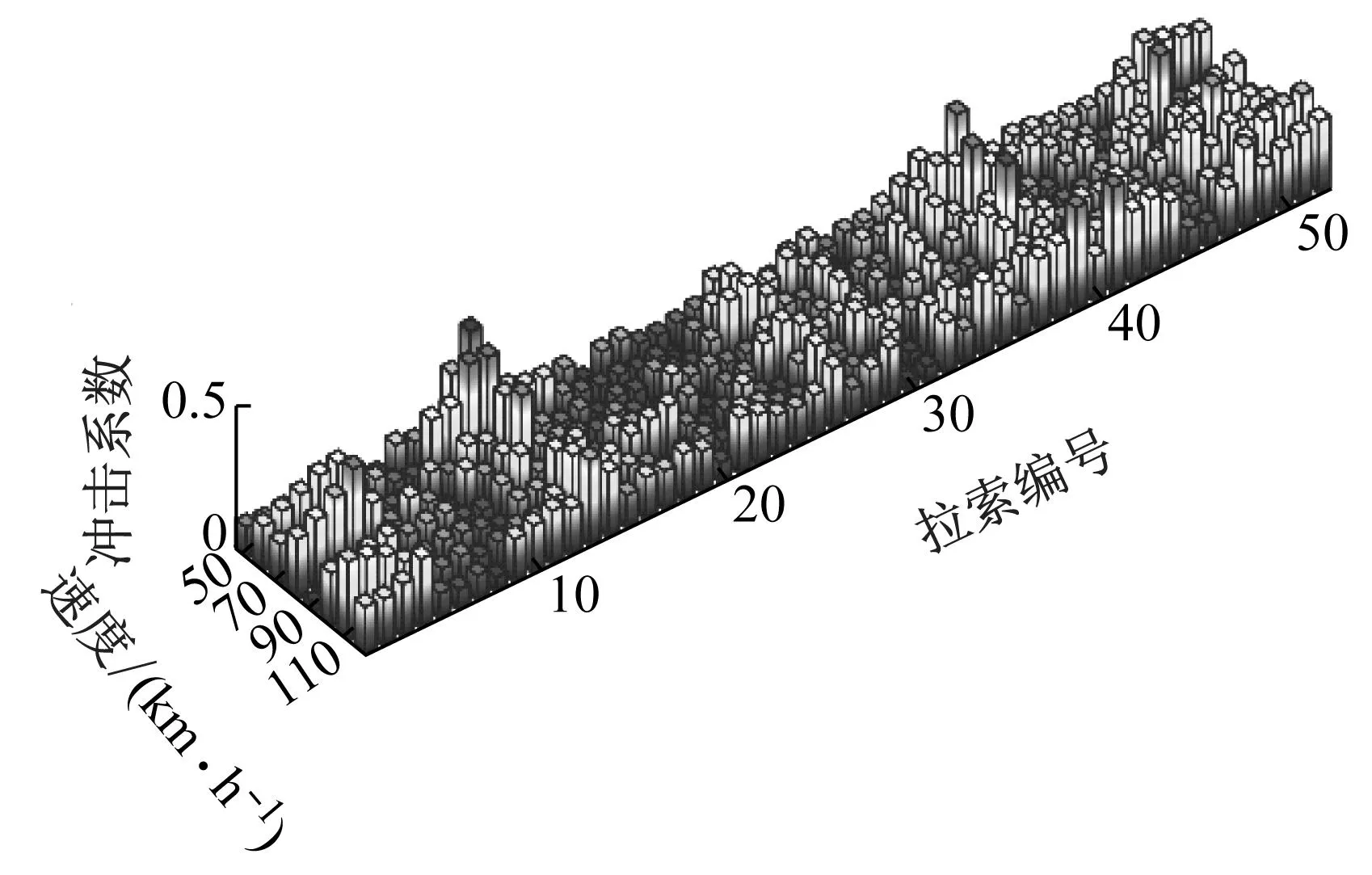
(a) 上行侧拉索动力冲击系数

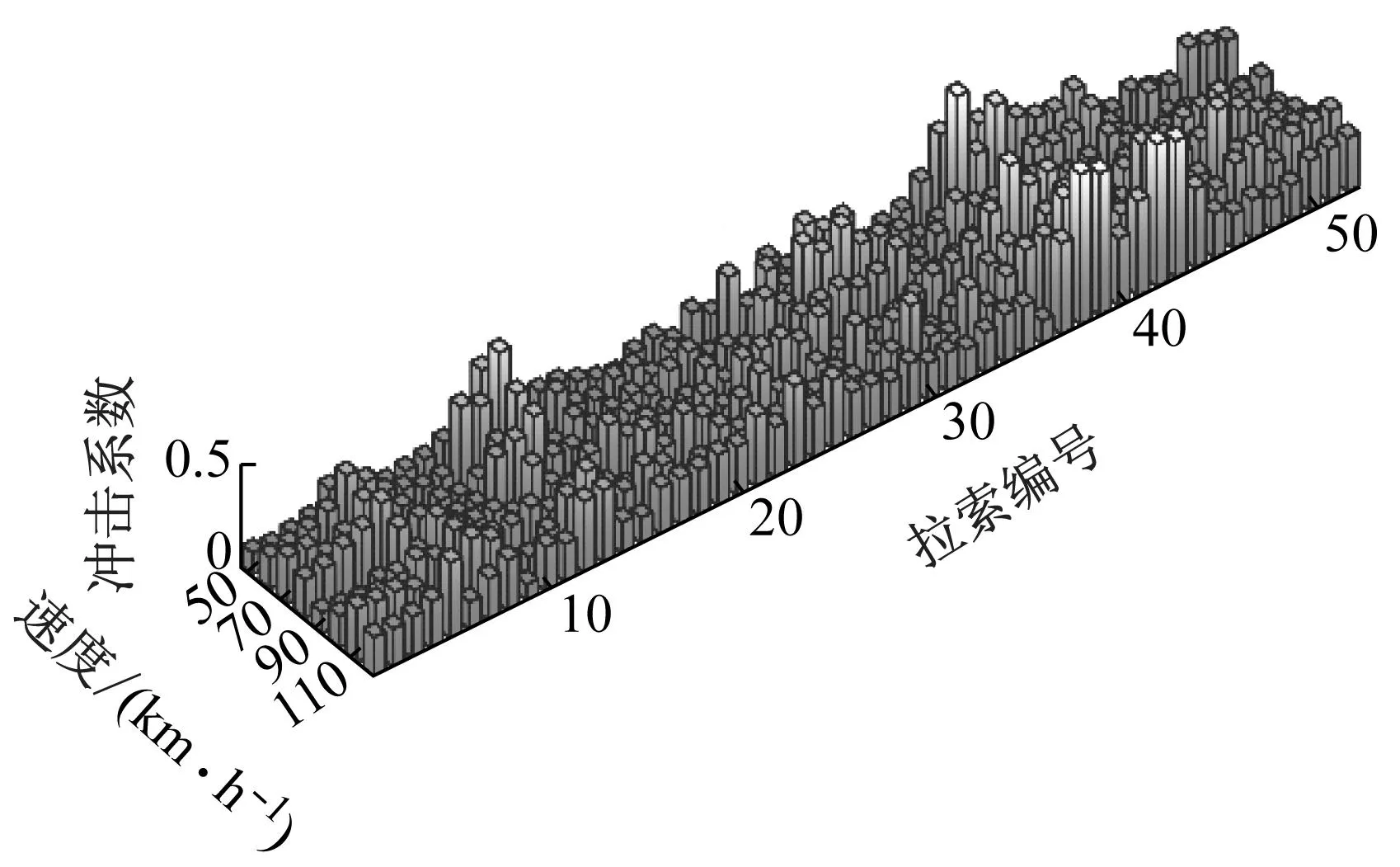
(b) 下行侧拉索动力冲击系数图6 单侧拉索动力冲击系数分布(A级,车道1)Fig.6 Distribution of dynamic impact coefficient of unilateral cable (Class A, Lane 1)

由图6可知,速度对斜拉索的动力冲击系数的影响对于每一根拉索都呈现出不一样的变化,即拉索的动力冲击系数受到速度变化的影响各异,但结合图6(a)、(b)两者发现,动力冲击系数较大的地方一般出现在桥塔短拉索附近,这与短拉索的刚度较大有关。

选取8根具有代表性的拉索,分别为边跨与中跨长拉索、桥塔附近短拉索,在路面等级为A级,车辆行驶车道1的工况下进行分析,结果如图7所示。可以发现该工况下动力冲击系数最大值出现在25号拉索在车速为50 km/h时,达到0.408,最小值出现在1号拉索在车速为90 km/h时,为0.034。

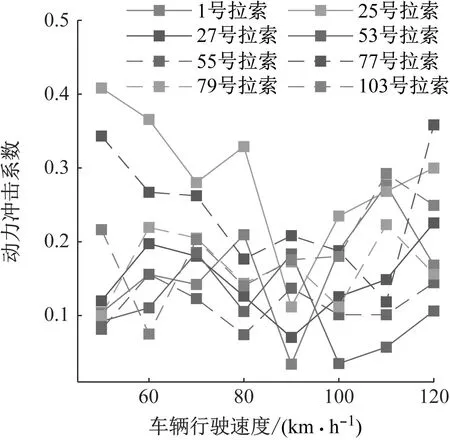
图7 拉索动力冲击系数(A级,车道1)Fig.7 Cable dynamic impact coefficient (Class A, Lane 1)

3.2.2 路面不平度的影响

随着路面不平度的增加,路面的起伏程度也急剧加大,从而车辆行驶过桥梁产生的动力响应也明显增大。对于不同路面等级下,单根拉索的应力时程曲线如图8所示。由图8可知,可知随着路面等级的增加,拉索产生的动力响应也会相应增大。

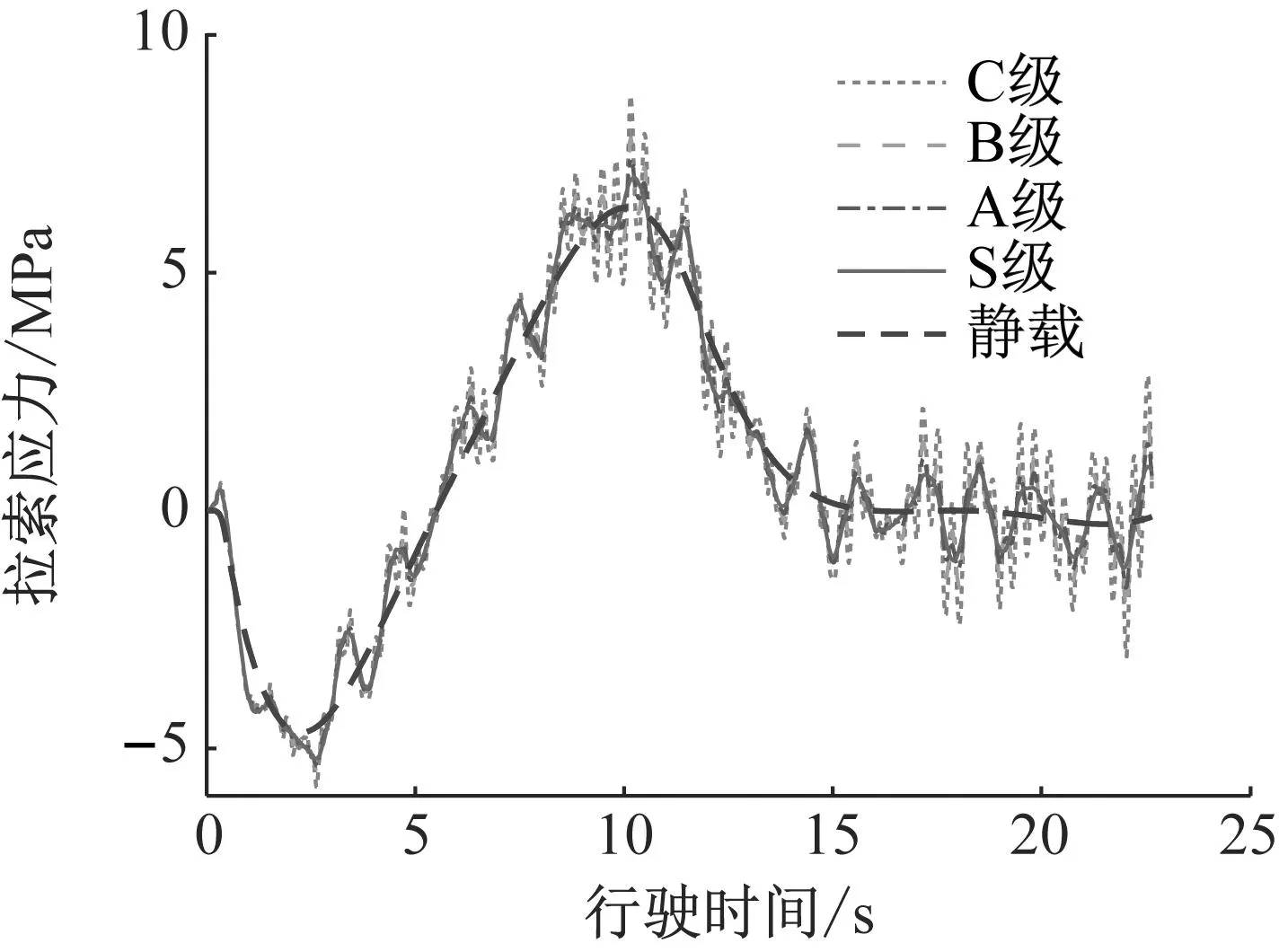
图8 单根拉索的应力时程曲线(120 km/h,车道2)Fig.8 Stress time history curve of a single cable (120 km/h, Lane 2)

对不同速度下,受路面等级变化计算的拉索的动力冲击系数进行汇总,如图9所示。随着路面不平度的增加,拉索的动力冲击系数也有所增加,且随着路面等级的不断增加,路面条件变差,拉索的动力冲击系数增加程度也越大,且在桥塔附近处较为明显。

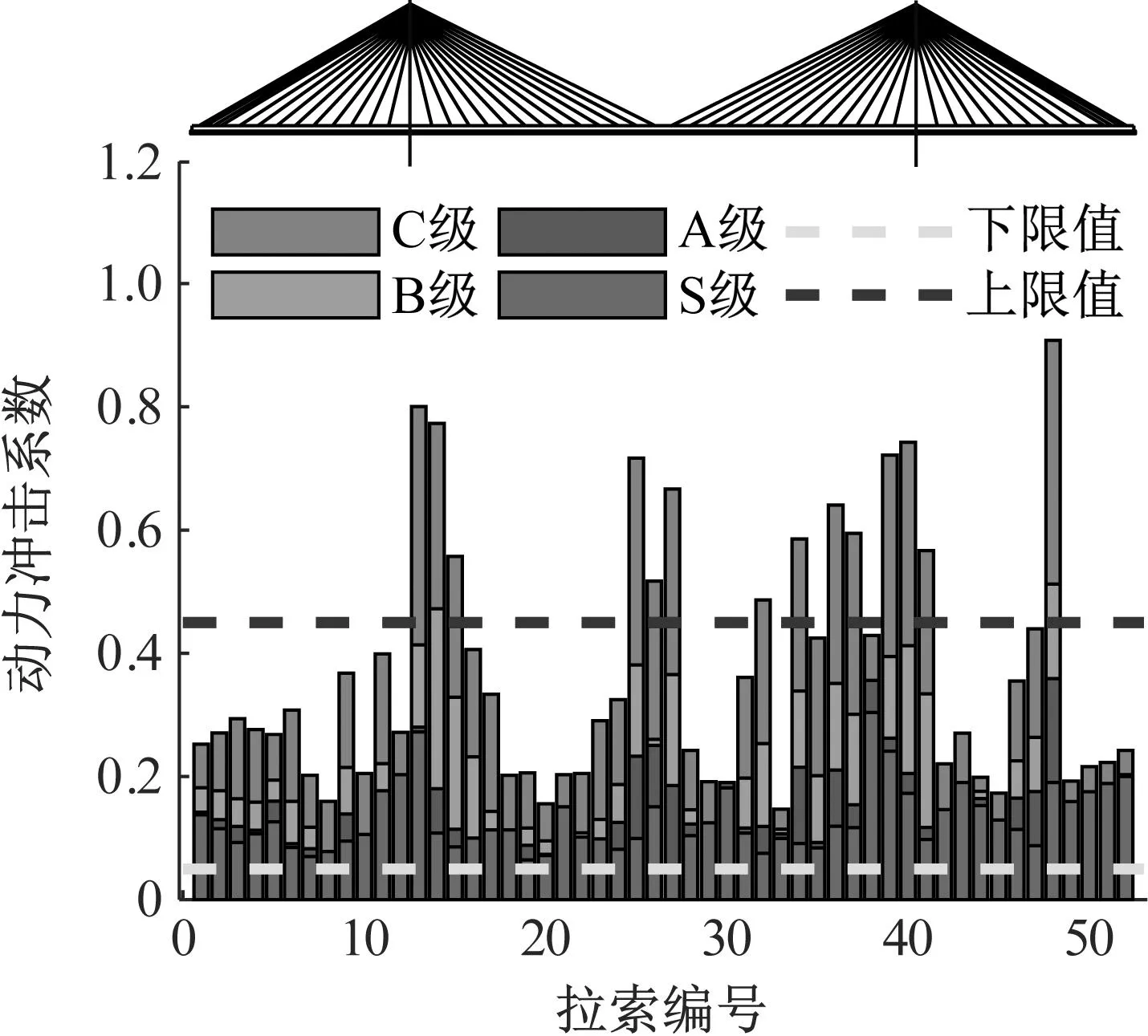
图9 路面等级动力冲击系数分布(80 km/h,车道1)Fig.9 Distribution of dynamic impact coefficient at road level (80 km/h, Lane 1)

相比较国家规范,可以发现,任何一种路面等级下的拉索的动力冲击系数均要大于国家规范给定的下限值0.05,而随着路面等级的不断提高,当达到C级路面时,有接近30%的拉索超过了国家规范给定的上限值0.45。然而由计算可知该斜拉桥的自振频率约为0.153 24 Hz,按照规范,其设计时的动力冲击系数应该取得下限值0.05,小于实际计算所得值,可以发现规范取值偏不安全。

3.2.3 车辆横向位置的影响

单个车辆行驶的横向位置相对于整个桥会产生偏心作用,从而导致拉索冲击系数的变化。因此,对于车辆行驶在不同横向位置产生的动力冲击系数也会发生变化,其计算结果如图10所示。其中箱型图红线表示动力冲击系数中位数,方框上、下边缘分别表示上、下四分位数,上、下横线分别表示数据集的上、下边缘,十字表示该数据集的异常值。

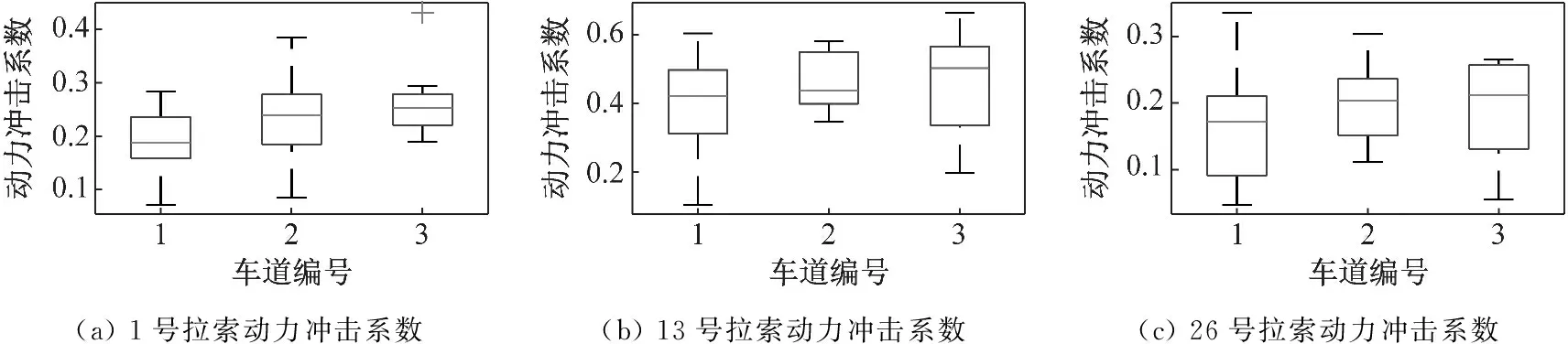
图10 不同车道对于动力冲击系数的影响(B级)Fig.10 The Influence of Different Lanes on the Dynamic Impact Coefficient (Class B)

可以发现,当车辆行驶的位置靠近拉索时,即车道编号从1～3,对拉索产生的动力系数会逐渐增大。比较不同位置处的拉索动力冲击系数可以发现,边跨的长拉索(1与52)在对于不同速度情况统计下的拉索动力冲击系数离散性较小;在桥塔附近的短拉索(13与40)的动力冲击系数中位数大于边跨长拉索位置处(1与52)的动力冲击系数,最大可以达到0.5,且两者都大于跨中长拉索(26和27)的动力冲击系数中位数。比较最大值可以发现,短拉索的动力冲击系数最大值均大于0.35,而长拉索绝大部分均在0.35以下。因此由上分析可知,在选取的典型拉索中,短拉索位置处的动力冲击系数会大于长拉索。

将不同车道下拉索动力冲击系数的分布进行统计,绘制出如图11所示的拉索动力冲击系数分布图。可以发现,在不同的路面等级下,拉索的动力冲击系数均大于规范下限值0.05,随着车辆行驶位置逐渐靠近边缘(从车道1移动到车道3),拉索的动力冲击系数逐渐增大,且部分拉索超过规范上限值0.45。对于A级路面,拉索动力冲击系数基本在规范之内,最大值在车道3时出现,为0.51,而B级路面车辆行驶在车道3时,动力冲击系数最大值0.894,且有15%的拉索动力冲击系数超过规范上限。

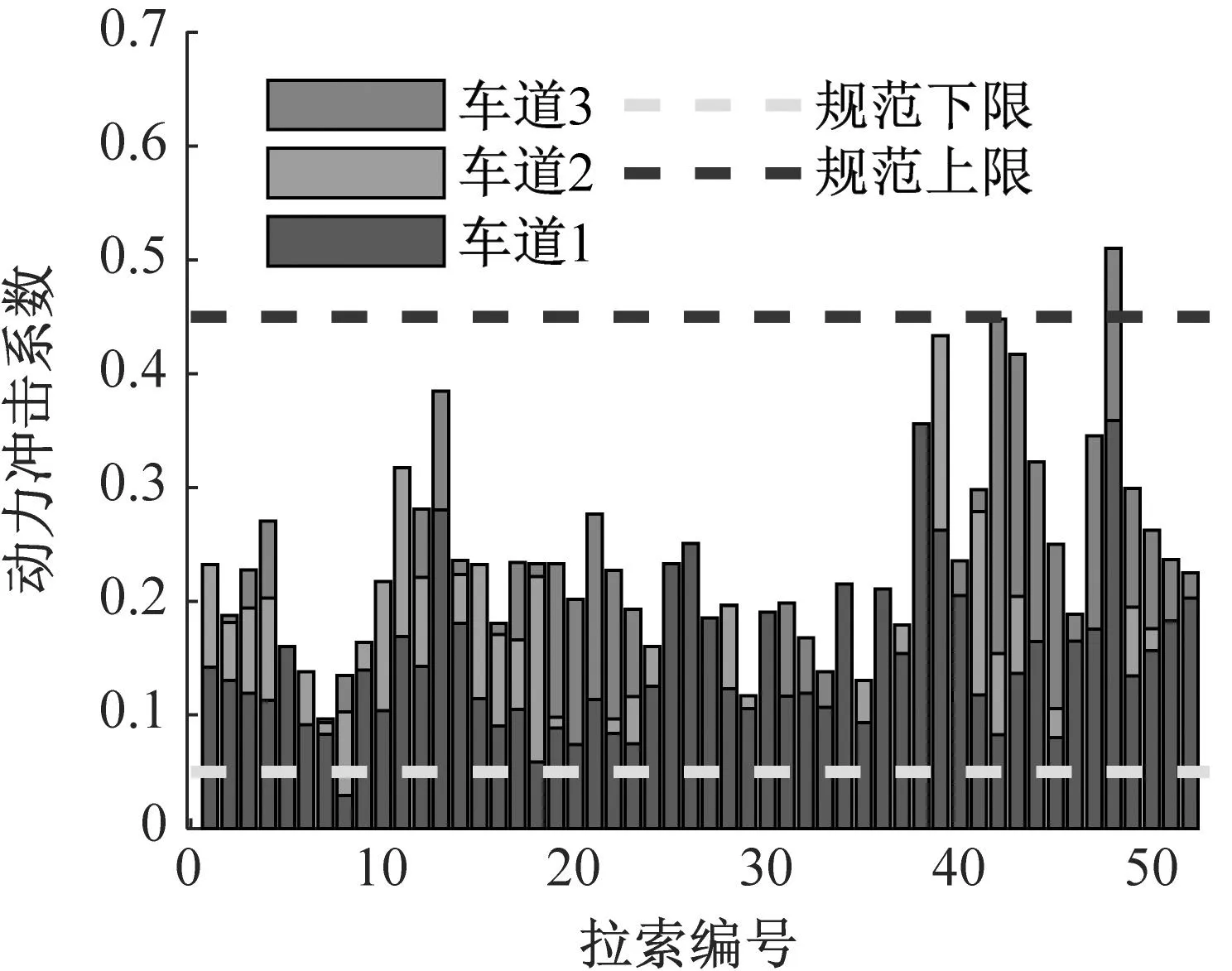
(a) A级路面

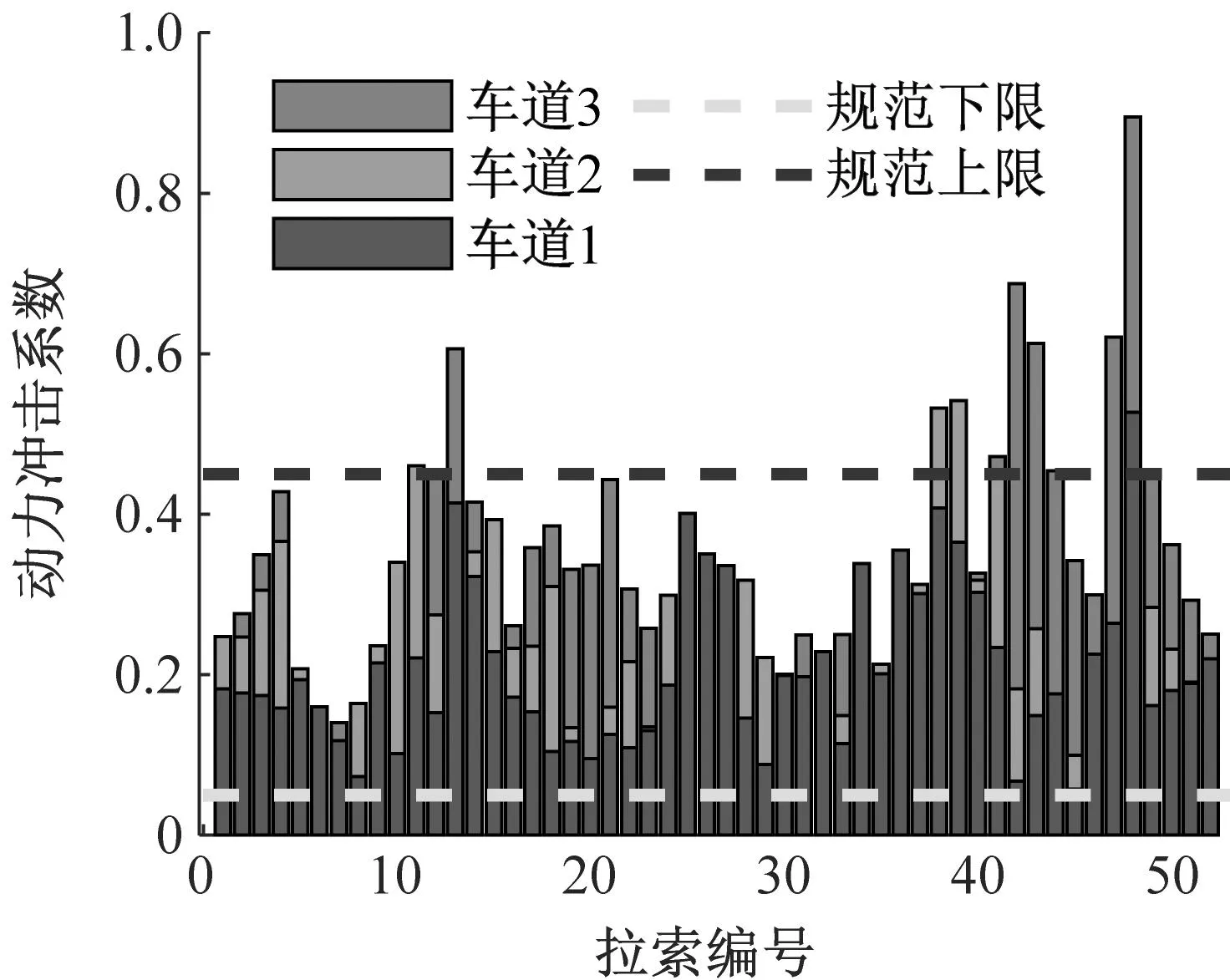
(b) B级路面图11 不同横向位置拉索动力冲击系数分布(80 km/h)Fig.11 Distribution of dynamic impact coefficient of cables at different lateral positions (80 km/h)

同时结合图6可以发现,不同行车方向对于拉索动力冲击系数也会造成影响。就短拉索而言,上游侧(车辆驶入侧)的拉索动力冲击系数要小于下游侧(车辆驶出侧),因此计算时还需考虑车辆行驶方向。

4 结 论

本文以国内某在役斜拉桥和某五轴重车作为研究对象,研究了斜拉桥拉索动力冲击系数。数值案例研究中考虑了不同车速、路面等级以及横向位置等工况,得出以下结论:

(1) 路面等级是影响拉索动力冲击系数的主要因素,随着路面等级的增加,动力冲击系数也加速增大。

(2) 边缘车道上车辆产生的冲击效应大于中间车道的冲击效应,对于短拉索,受外侧车道的影响更为明显。

(3) 经统计分析,发现桥塔附近的短拉索的动力冲击系数较大,是斜拉索维修与养护关注的重点。

(4) 经研究发现国家规范给定的冲击系数(0.05)偏不安全,综合考虑下,建议根据路面等级选取合理的拉索冲击系数,建议值如下:光滑路面取0.08,A级路面可取0.15,B级路面取0.25,C级路面取0.40。对于桥塔附近短拉索设计时可以适当放大。