基于改进经验小波变换的海洋平台结构模态参数自动识别方法

冷建成, 刁凯欣, 庞 哲, 冯慧玉

(1. 东北石油大学 机械科学与工程学院, 黑龙江 大庆 163318;2. 东北石油大学 三亚海洋油气研究院, 海南 三亚 572025)

海洋平台作为油气资源开发的主要设施,长期受到环境、人为、老化因素的影响,会产生不同程度的结构损伤,损伤的不断累积会导致部分结构失效,对平台的安全运营产生极大隐患。为此在平台上布置结构健康监测系统,可以辅助管理人员把握平台的整体结构参数及损伤演化规律,是保障平台健康服役的有效手段之一。由于振动信号易于测量和采集,而且监测过程无需中断结构的正常运行或需要特定的激励设备,可实现实时监测并在整体上评估结构损伤,因此振动监测技术具有很高的应用价值,而模态参数识别是该技术的基础[1]。

模态参数识别是指通过分析结构动力响应数据,获取固有频率、阻尼比、模态振型等参数的过程[2]。海洋平台在环境激励、作业激励、温度变化的作用下,其振动响应信号属于幅值、频率波动的非线性、非平稳信号,以傅里叶变换为基础的频域分析方法处理此类信号具有一定的局限性[3]。

相关学者提出希尔伯特-黄变换(Hilbert-Huang transform,HHT)[4]、小波变换(wavelet transform,WT)[5]等时频域分析方法,在非线性、非平稳信号处理上具有很好的优越性。HHT中经验模态分解(empirical mode decomposition,EMD)算法缺乏理论基础,容易出现端点效应和模态混叠;WT拥有严格的理论基础,但需要设定小波基函数等参数,且容易受到噪声影响,自适应性较差[6]。

Gilles[7]在HHT算法与WT算法的基础上,提出了经验小波变换(empirical wavelet transform,EWT),该方法基于傅里叶频谱划分频带分割边界,并构建小波滤波器将信号分解为若干子频带。由于EWT算法以傅里叶频谱为基础确定分割边界,当信号信噪比较低时,频谱的“毛刺”会影响边界的划分,导致方法失效。万熹等[8]基于Burg算法构造自回归(autoregression, AR)功率谱,用于替换傅里叶频谱进行边界划分,该方法能够抑制噪声对频谱模态峰值的干扰,提高了频谱分割的准确度,成功应用于香港汀九斜拉桥的模态参数识别。Fang等[9]基于Yule-Walker算法构造AR功率谱进行频谱划分,解决了桥梁GNSS数据噪声过大的问题,实现了某桥梁的模态参数识别。Amezquita-Sanchez等[10]使用多信号分类(MUSIC)算法进行频谱分割,并将该方法应用于乐天大厦的模态参数识别。黄书亭等[11]提出了一种结合数学形态学的改进经验小波变换方法,并将该方法应用到南京长江大桥的模态参数识别中。以上算法主要针对频谱进行降噪来提升频谱分割的准确性,但是频谱降噪与边界自动划分的结合方面需要进一步深入研究。

为此,本文基于EMD算法的自适应性及EWT算法的模态分解正交性,引入奇异值谱和尺度空间算法,提出一种改进经验小波变换方法,并结合随机减量技术和希尔伯特变换,以实现环境激励下结构的模态参数自动识别。

1 IEWT方法

1.1 经验小波变换

经验小波变换以傅里叶频谱为基础,确定分割边界,并以此构造小波滤波器组将信号分解为一系列的调幅调频单分量信号,其基本原理如下所述。

首先,预设单分量信号的数目为N,对信号x(t)进行傅里叶变换,并对其进行正则化,获得傅里叶频谱x(ω),其中ω∈[0,π];其次,遍历频谱x(ω)的局部极大值,并对其进行降序,提取前N个极大值,以相邻极大值之间的最小值作为频谱的分割边界x=ωn;再次,根据分割边界,以ωn为中心构造宽度为2τi过渡段,傅里叶频谱被划分为N个连续区间Λn,如式(1)所示,并以此构造经验尺度函数φn(ω)与经验小波函数ψn(ω),如式(2)～式(3)所示;最终,信号x(t)分解为调频调幅组分,如式(4)～式(5)所示。

Λn=[ωn-1,ωn],n=1,2,…,N

(1)

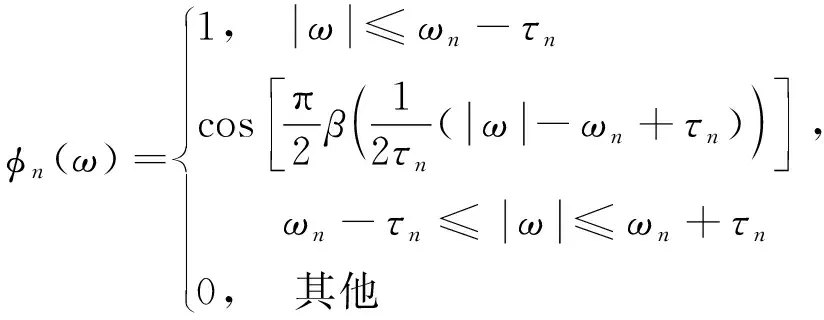
(2)

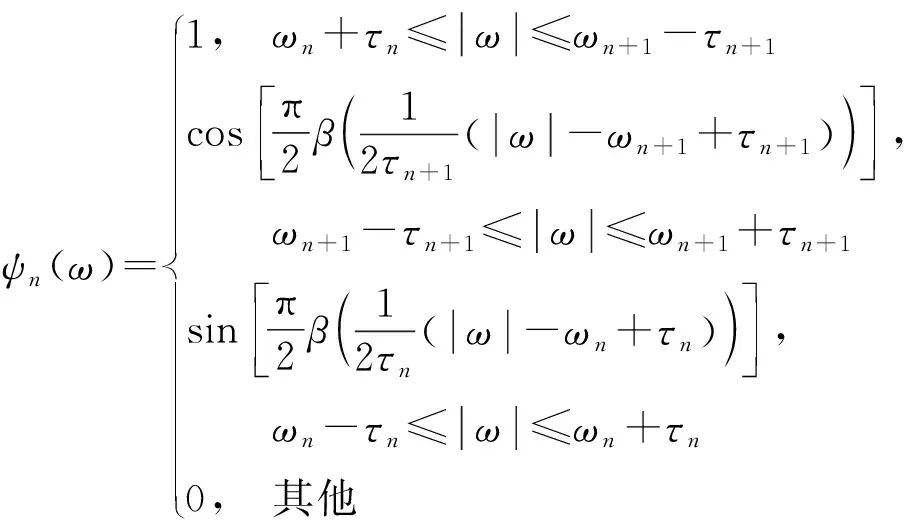
(3)

式中,β(x)=x4(35-84x+70x2-20x3)。

(4)

(5)

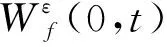
1.2 改进经验小波变换

由上述经验小波变换原理可知,傅里叶频谱的分割边界主要依赖局部极大值的选择,当所测信号信噪比较低,傅里叶频谱中模态峰值附近存在若干紧密分布的“毛刺”,会影响分割边界的确定,导致频谱分割失效。

为减少噪声对信号分解的影响,提出改进经验小波变换(improved empirical wavelet transform,IEWT)方法,该方法结合了奇异值分解法及尺度空间法,在分割边界确定方面对EWT方法进行改进,实现傅里叶频谱降噪和分割边界自适应划分。

(1) 奇异值分解法

根据Brincker等[12]提出的频域分解法,构造待测信号的功率谱密度矩阵,对其进行奇异值分解(singular value decomposition,SVD),如式(6)所示,能够将多自由度系统转换为单自由系统的叠加,在密集模态的模态参数识别中具有较好的效果。

(6)

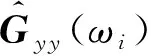
由于奇异值对应单自由度系统的功率谱密度函数,且第一奇异值曲线包含了大量的模态信息,选择该曲线构造奇异值谱,能够有效降低噪声对模态峰值干扰。

(2) 尺度空间法

针对频谱中的模态峰值判定问题,Liutkus[13]提出了尺度空间峰值拾取(scale-space peak picking,SSPP)方法,通过使用不同尺寸的核(加权窗口)平滑数据,以迭代的方法确定峰值。

SSPP方法在迭代过程中,会建立一个C准则用于峰值估计,当发现潜在峰值时,C准则的值会变大,迭代结束后,可基于C准则直接进行峰值拾取,具体步骤如下:

步骤1初始参数输入

设定待测信号v是维数为N×1的列向量,C准则的初始值为N×1的零向量,目标峰值数为K,峰值阈值为ρ,其中ρ∈[0,1]。

步骤2峰值估计准则初始化

检出信号v中所有局部极大值,存储于集合P中,如式(7)所示。若v(n)为局部极大值(n为位置索引),则v(n)应大于相邻数据,如式(8)所示。

P←localmaxima(v)

(7)

v(n)∈P⟺v(n)=max[v(n-1),v(n),v(n+1)]

(8)

由于待测信号v未经平滑处理,包含较多噪声,且集合P中的局部极大值点是基于待测信号v求得,需要进一步处理。在第一次迭代中,将所有的局部极大值存储于C准则中,如式(9)所示。

∀p∈P,C(p)←v(p)

(9)

另外,将所选峰值也存储于集合O中,即O←P。

步骤3峰值迭代求解

选择一个长度尺度s对待测信号v进行平滑,降低噪声对信号的影响,获得新的平滑信号v。在实际应用中,数据平滑可由信号v与加权窗口(如长度为s的标准化汉明窗)的卷积实现。

对信号进行数据平滑后,重新检测局部极大值,得到新的集合P,如式(7)及式(8)所示。将新的局部极大值与集合O中已确定的极大值点相关联,若某些局部极大值点被再次选中,将在后续处理中增加这些点的C准则。

由于数据平滑后,局部极大值点会发生漂移,需要确定集合O中哪些元素最接近集合P,从而建立近邻集合I,如式(10)所示。

(10)

如式(10)所示,确定了集合O与集合P的近邻集合I,该集合即为平滑后的被再次被选中的局部极大值点。依据近邻集合I,增加对应点的C准则,如式(11)及式(12)所示。

∀p∈P, ΔC(I(p))←v(I(p))s2

(11)

∀n,C(n)←C(n)+ΔC(n)

(12)

不断重复上述过程,并每次迭代都增加尺度s,并增加C准则的值,一般迭代30次即可。

步骤4峰值结果输出

将C准则进行降序排序,依据预设的目标峰值数K或峰值阈值ρ进行峰值选择。

若求解峰值数K已知,选取C准则中的前K个值对应的点作为峰值输出结果;若峰值阈值ρ已知,将C准则进行归一化处理,选取大于阈值ρ的点作为峰值输出结果。

通过以上方法的改进,EWT方法中傅里叶频谱被替换为信噪比较高的奇异值谱,尺度空间法自适应地确定模态峰值与分割边界,结合小波滤波器组将信号分解为噪声分量与若干固有模态函数(intrinsic mode function,IMF)分量。

1.3 模态参数自动识别

在对结构进行实时监测分析时,需要重视数据分析的实时性及数据分析的准确性。对于实时监测的数据流,可采用滑动数据窗的形式对数据流进行分段截取,再进行后续的模态分析,其基本原理如图1所示。其中,分析间隔Δt与数据的实时性有关,每次分析数据长度t与该段数据频谱的分辨率有关。选择合适的分析间隔Δt和每次分析数据长度t对于数据的实时性及后续分析的准确性尤为重要。

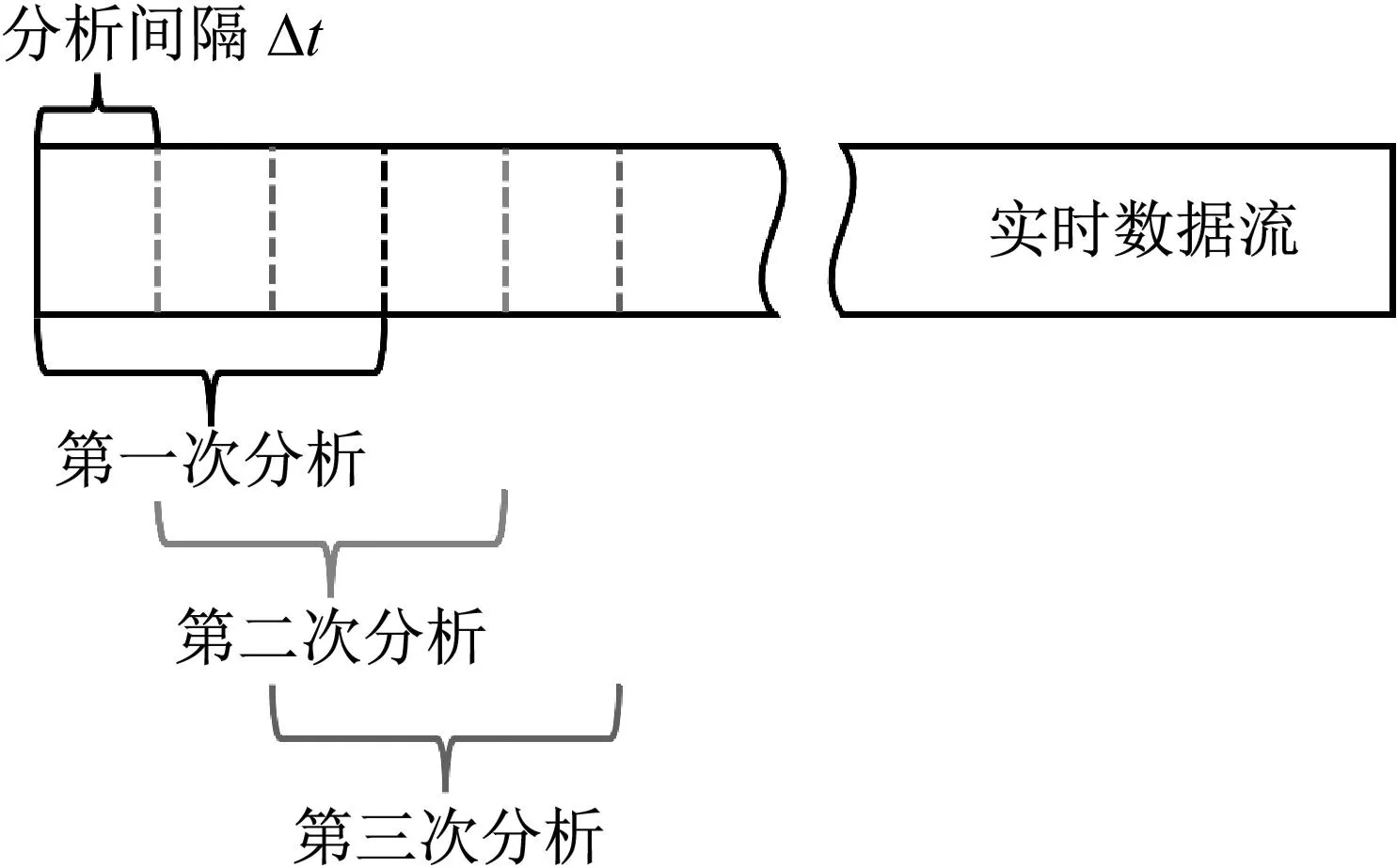
图1 滑动数据窗原理Fig.1 Principle of sliding data window

实时监测数据流经过滑动数据窗分段后,采用IEWT方法获得该段数据的IMF分量,进而采用随机减量技术与希尔伯特变换相结合的方法,实现频率及阻尼比等模态信息的识别。

(1) 随机减量技术

随机减量技术(random decrement technique,RDT)是一种从环境激励下结构响应信号中提取自由衰减响应的处理方法[14]。

设y(t)为随机激励下某线性系统的单自由度振动响应信号,选取一个固定值A对y(t)的幅值进行截取(A的值通常为信号均方差的1.5倍),A与响应信号的交点为ti(i=1,2,…,N),获取N段以ti为起点,长度为s的时间序列。

对以上N段时间序列进行叠加平均即可获得y(t)的自由衰减响应信号x(t),如式(13)所示。

(13)

由于IEWT方法获得的IMF分量只包含单一频率,属于单自由度振动响应信号,可采用RDT方法获取对应的自由衰减响应信号。

(2) 希尔伯特变换

希尔伯特变换(Hilbert transform,HT)可对自由衰减信号进行处理,获得幅值曲线和相位曲线,实现模态频率及阻尼比的识别。

设xj(t)为RDT方法获得的某自由衰减响应信号,如式(14)所示。

xj(t)=A0je-ξjωjtcos(ωdjt+φj)

(14)

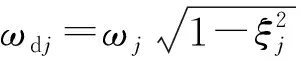
对式(14)进行希尔伯特变换,得到相位函数θj(t)及幅值函数Aj(t),如式(15)～式(16)所示。

θj(t)=ωdjt+φj

(15)

Aj(t)=A0e-ξjωjt

(16)

对相位函数θj(t)求导可得第j阶有阻尼圆频率ωdj,对于实际的工程结构,阻尼比通常小于5%,故ωdj≈ωj,进而获得第j阶模态频率fj,如式(17)所示。

(17)

由于幅值函数Aj(t)为指数函数,构造指数衰减曲线对幅值函数进行拟合,如式(18)所示。

y(t)=A0ebt,b=-2πfjξj

(18)

曲线拟合之后可获得b的取值,进而获得第j阶阻尼比,如式(19)所示。

(19)

综上,提出了基于IEWT的模态参数自动识别方法,基于实时监测工况下的数据流,首先采用滑动数据窗方法进行数据分段;其次采用IEWT将分段数据分解为若干IMF分量;再次采用RDT&HT方法对各IMF分量进行模态参数识别;最终获得信号各阶模态的频率与阻尼比等信息,其基本流程如图2所示。

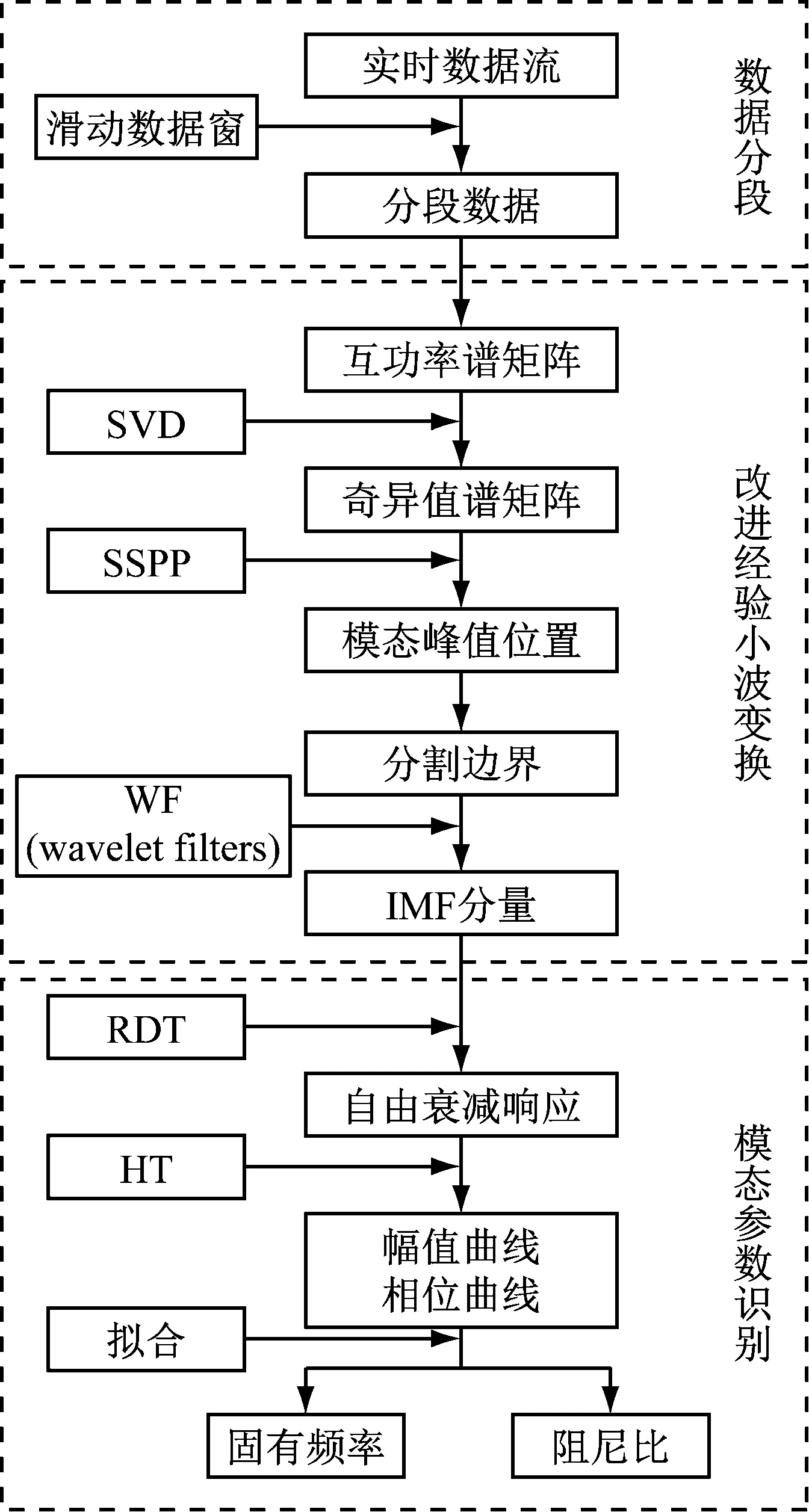
图2 模态参数自动识别流程图Fig.2 Flow chart of automatic identification of modal parameters

2 仿真信号分析

2.1 自由振动响应信号

构造三自由度结构的自由振动响应信号s(t),该信号由三个单分量信号s1(t)、s2(t)、s3(t)及信噪比为10 dB的高斯噪声n(t)组成,如式(20)所示。

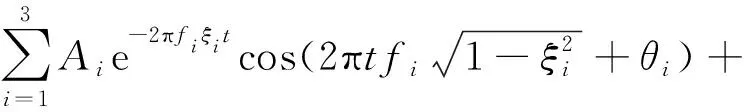
(20)

式中:Ai为幅值;fi为频率;ξi为阻尼比;θi为相角。各单分量信号的具体参数如表1所示。

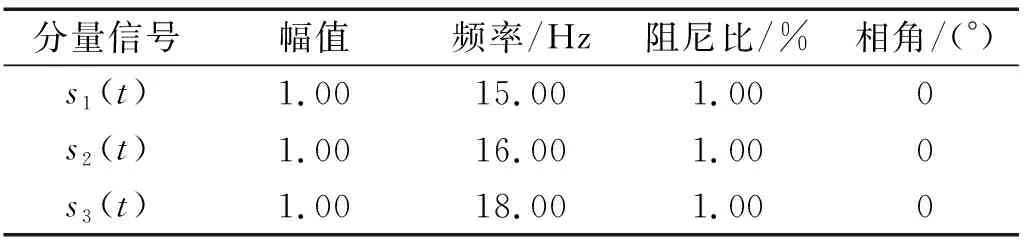
表1 各分量信号参数Tab.1 Signal parameters of each component

以100 Hz的采样频率获取30 s的数据进行波形展示,如图3所示。

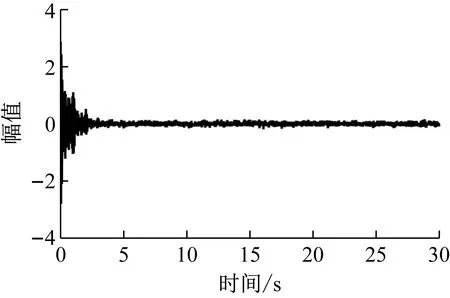
图3 自由振动响应信号时程图Fig.3 Time history chart of free vibration response signal

首先采用EWT算法对自由振动响应信号的傅里叶频谱进行分析,如图4所示。

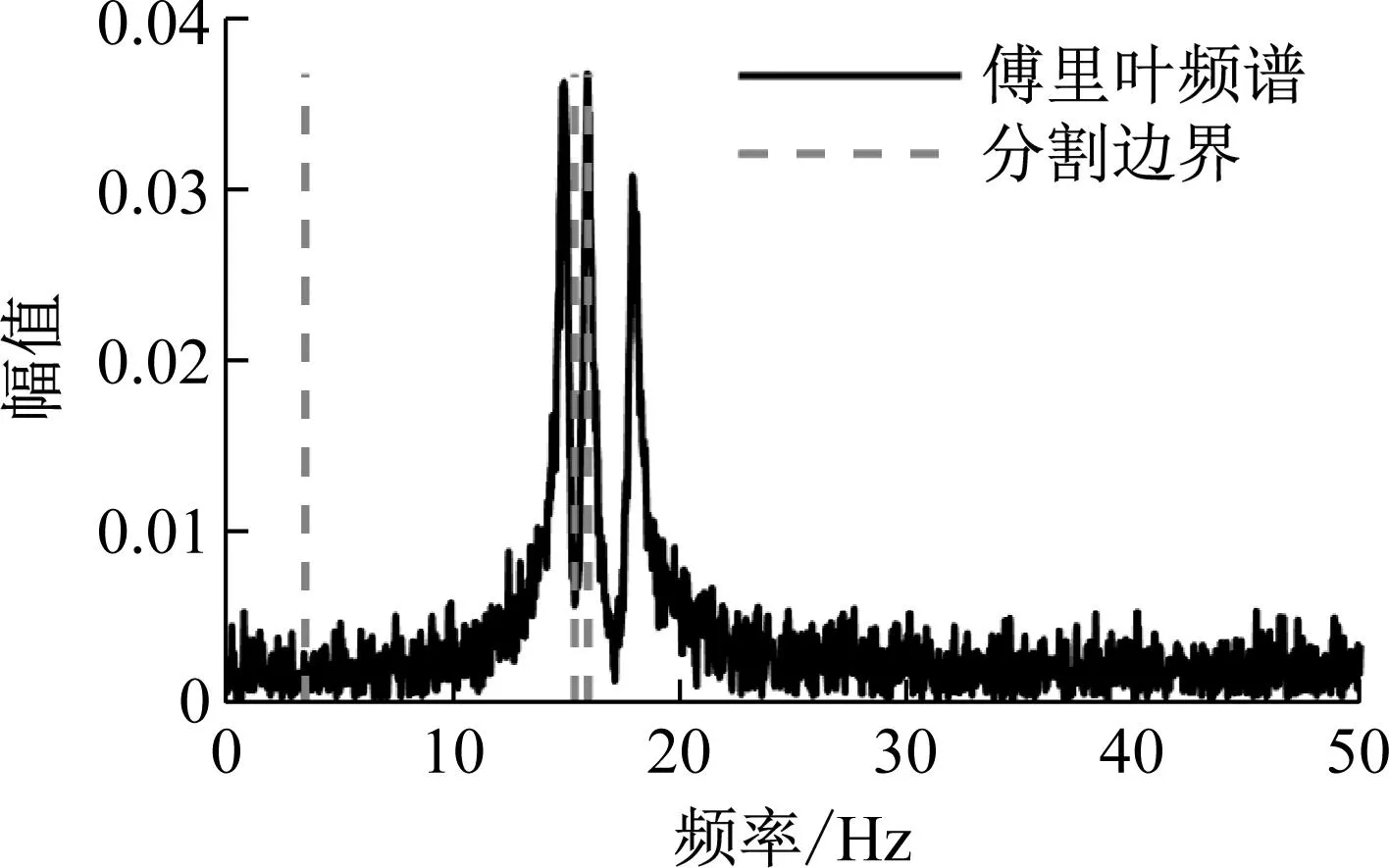
图4 傅里叶频谱分割边界Fig.4 Segmentation boundaries of Fourier spectrum

由图4可见,由于噪声干扰,傅里叶频谱第二个峰值被过度分割,导致频谱分割失效。下面采用IEWT方法进行分析:首先计算信号的互功率谱矩阵,对其进行奇异值分解,获得该信号的奇异值谱;其次,使用尺度空间法对奇异值谱进行峰值识别,并确定频谱的分割边界;最后将分割边界映射至傅里叶频谱中,计算结果如图5和图6所示。

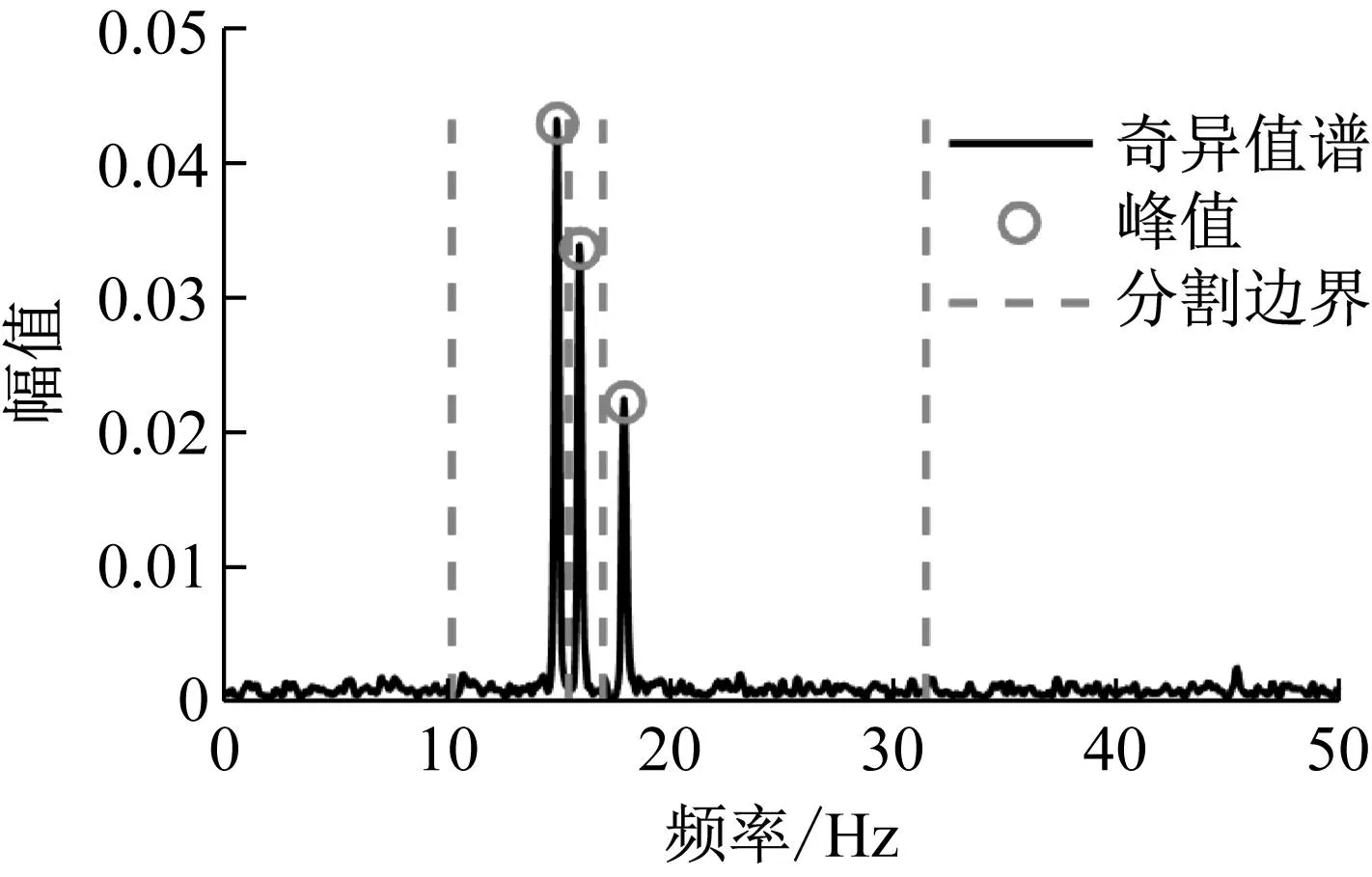
图5 奇异值谱及分割边界Fig.5 Singular value spectrum and boundaries

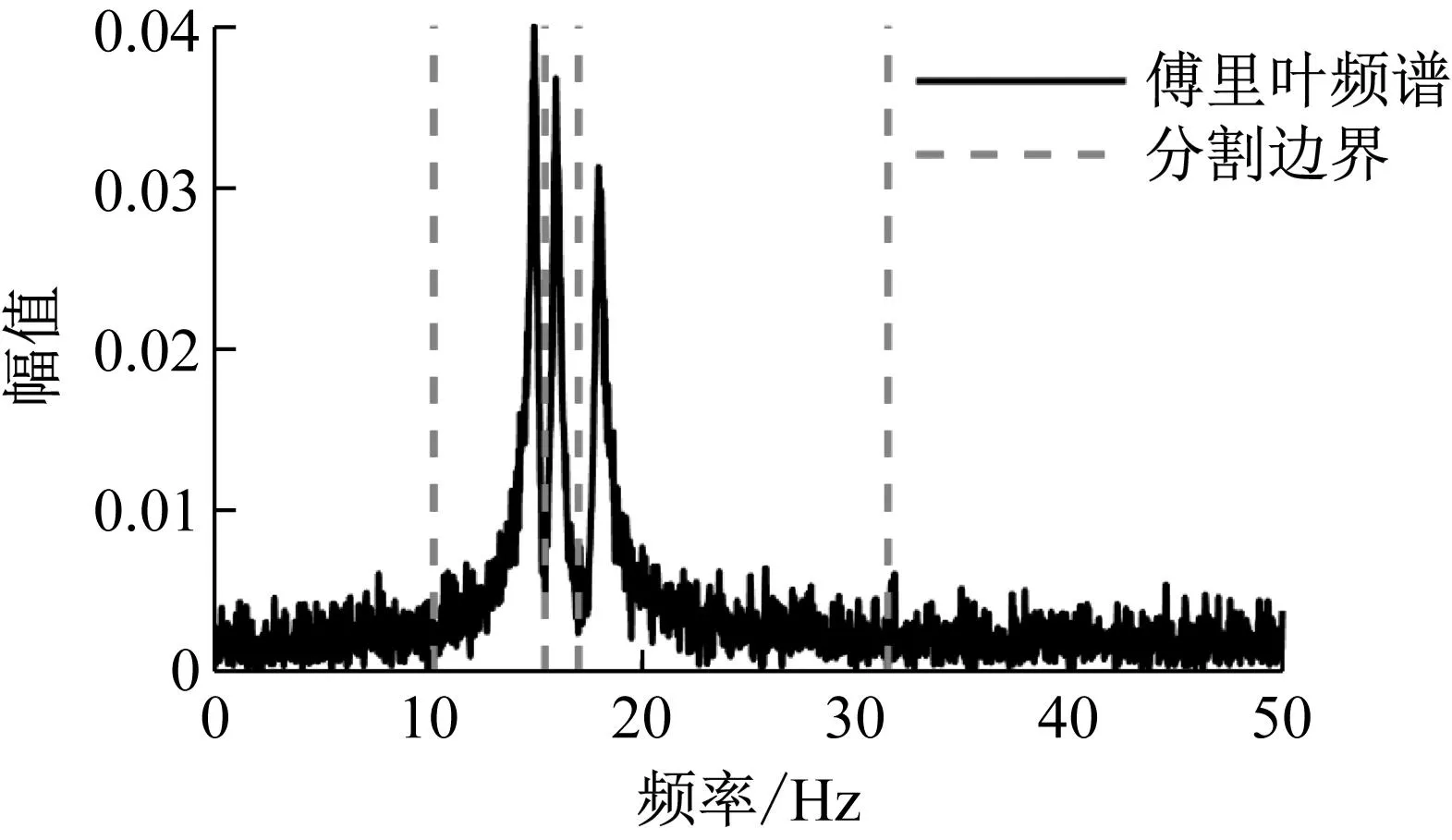
图6 傅里叶频谱分割边界Fig.6 Segmentation boundaries of Fourier spectrum

相比图4中的傅里叶频谱,图5中的奇异值谱噪声较低,各阶模态峰值突出,更便于进行峰值的识别与分割边界的划分。由图6中映射的分割边界可知,傅里叶频谱将被分割边界准确划分,与图4相比可见,IEWT方法具有很好的分割效果。

根据IEWT方法获取的分割边界,构造小波滤波器组对傅里叶频谱进行分割,并对分割结果进行逆傅里叶变换获得三个IMF分量,如图7所示。

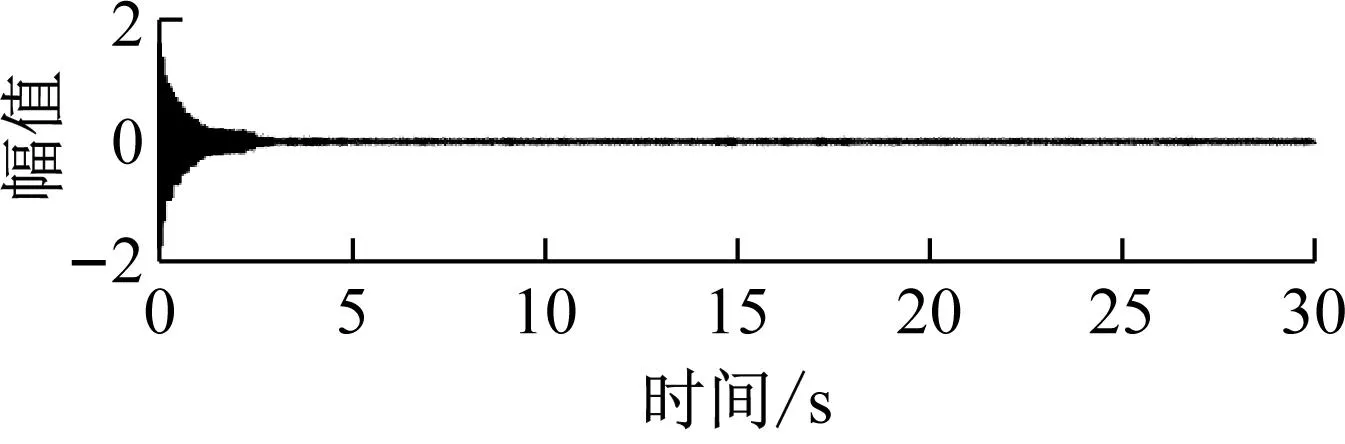
(a) 模态1

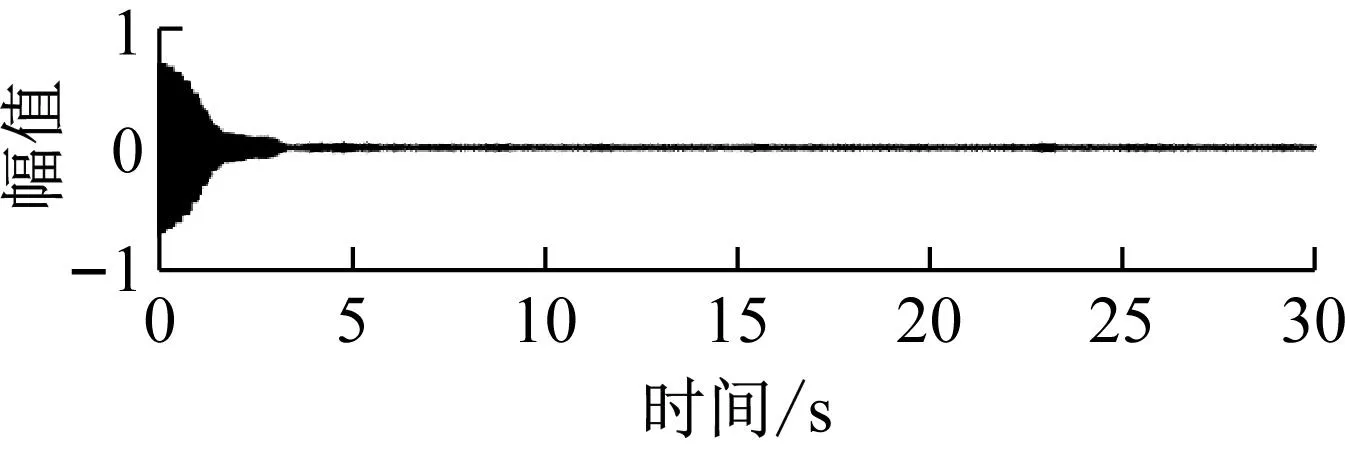
(b) 模态2

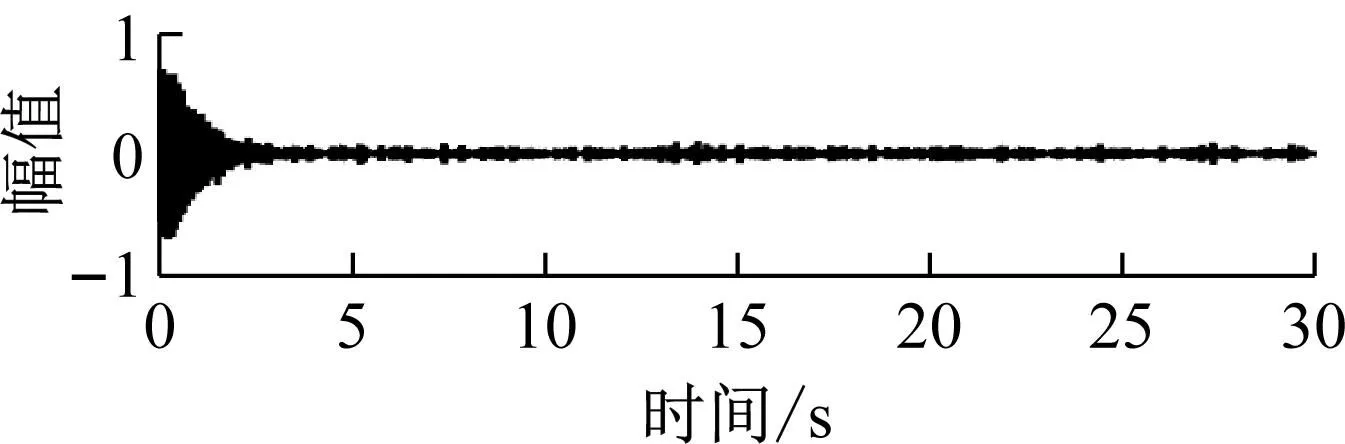
(c) 模态3图7 模态分量Fig.7 Modal components

由以上自由振动响应信号的分析结果可知,IEWT方法能够对低信噪比的密集模态信号进行频谱分割边界的自适应划分,进而精准获取信号的IMF分量。

2.2 ASCE Bechmark模型信号

为进一步评估IEWT方法在多模态信号处理中的效果,采用IASC-ASCE SHM Benchmark模型进行验证[15],该模型为4层2×2跨的钢结构模型。根据参数设置,选用12自由度无损结构进行分析,其中阻尼比为1%,以高斯白噪声模拟外部激励。选取x方向1#、2#、3#及4#传感器数据进行分析,各传感器分别布置于每层桁架的中点处,如图8所示。

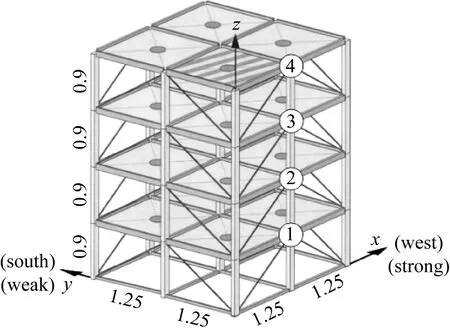
图8 Benchmark模型结构示意图(m)Fig.8 Structure diagram of Benchmark model (m)

基于Johnson等提供的MATLAB程序模拟该结构的动力响应,这里仅分析4#传感器的时程曲线,如图9所示。其中采样频率为1 000 Hz,采样时长为30 s。

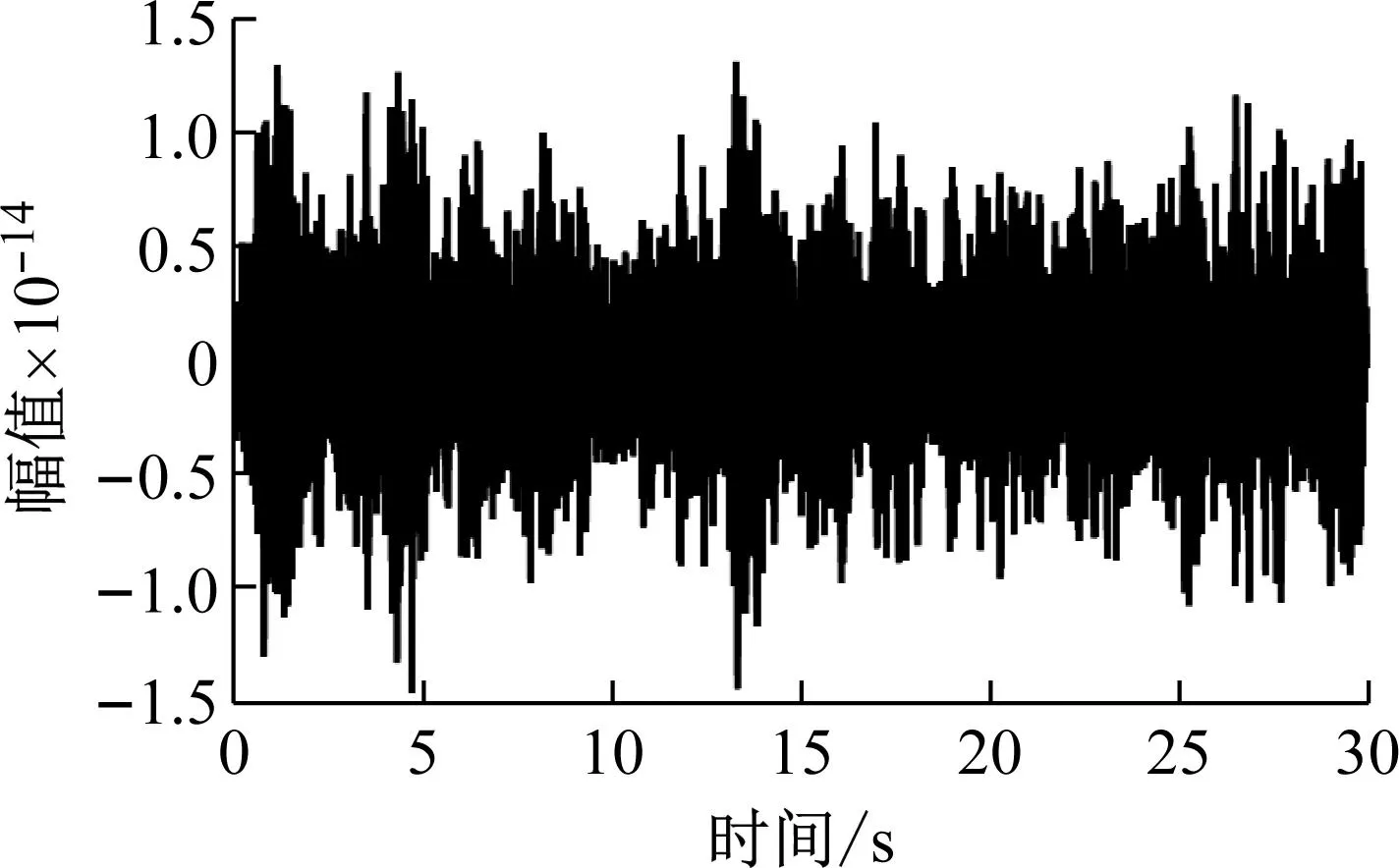
图9 传感器数据时程图Fig.9 Time history chart of sensor data

分别采用EWT方法和IEWT方法对该信号进行处理,其分割边界如图10和图11所示。

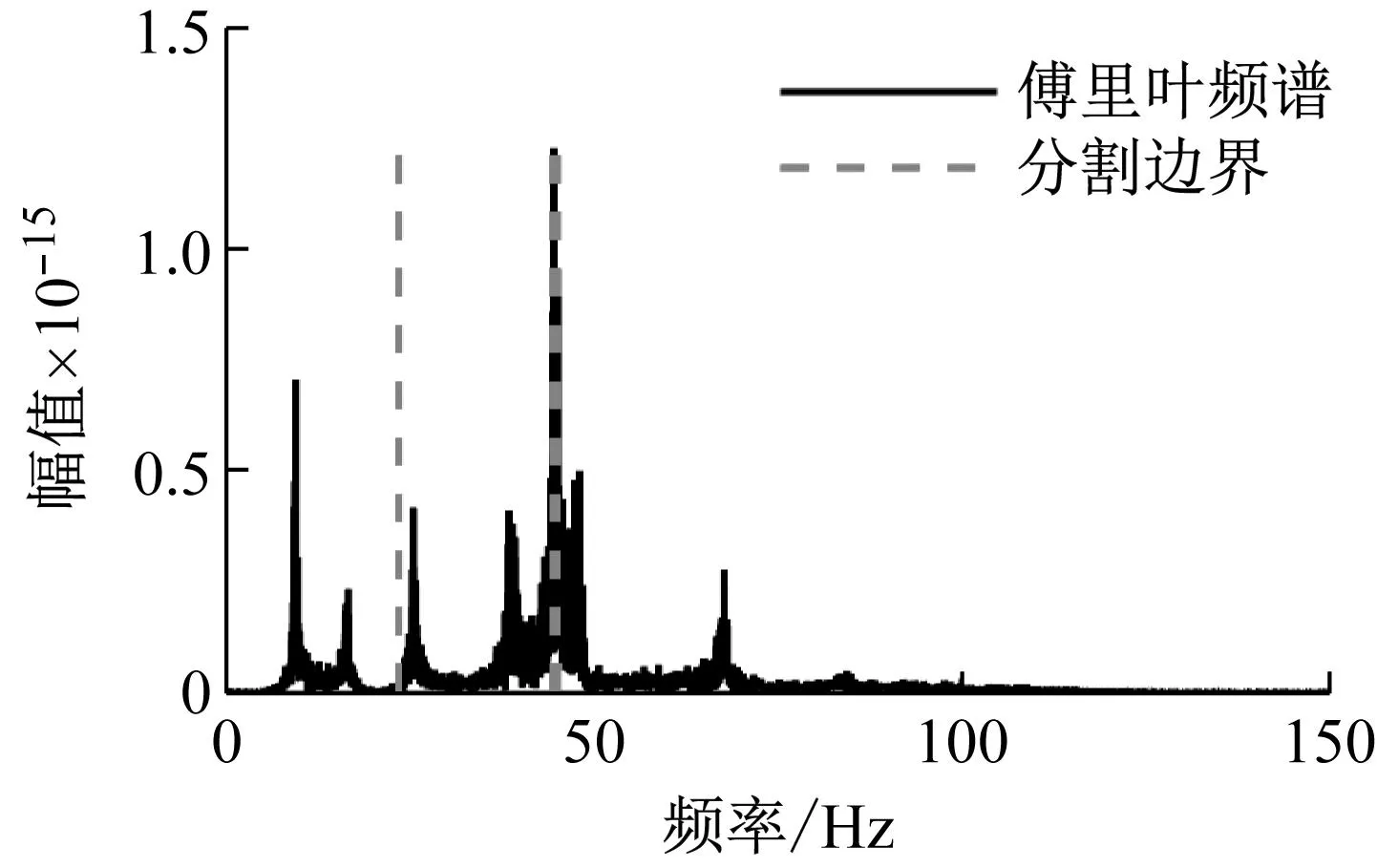
图10 傅里叶频谱分割边界Fig.10 Segmentation boundaries of Fourier spectrum

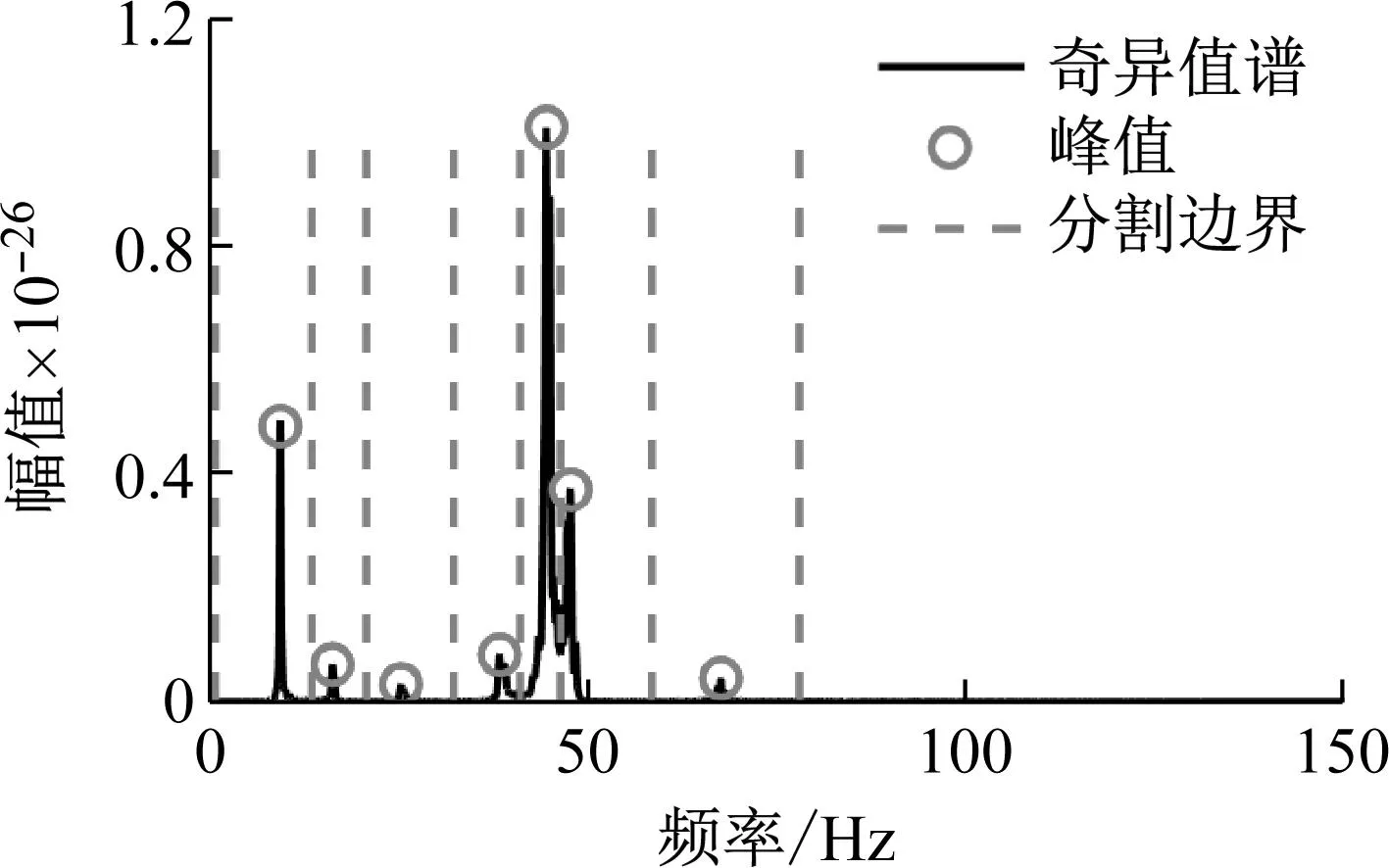
图11 奇异值谱及分割边界Fig.11 Singular value spectrum and boundaries

由图10可见,基于EWT的频谱分割方法无法准确检测到所有边界,其中前两阶频率被划分至同一个区间,发生了模态混叠;在50 Hz附近的频谱中,由于噪声干扰,EWT方法密集在此处划分了若干边界,傅里叶频谱被过度分割出若干无意义的频带。

相对应地,由图11可知,IEWT方法将奇异值谱分割为若干频带区间,各阶频率被准确划分至不同的频带中。第1、9频带用于隔离噪声,不参与模态参数识别。对比图10和图11可知,IEWT方法具有很好的自适应性,能够避免发生模态混叠及过度分割的问题。

将图11中的分割边界映射至傅里叶频谱中,如图12所示。构造小波滤波器组将傅里叶频谱划分至7个模态分量,其中前3阶模态分量如图13所示。

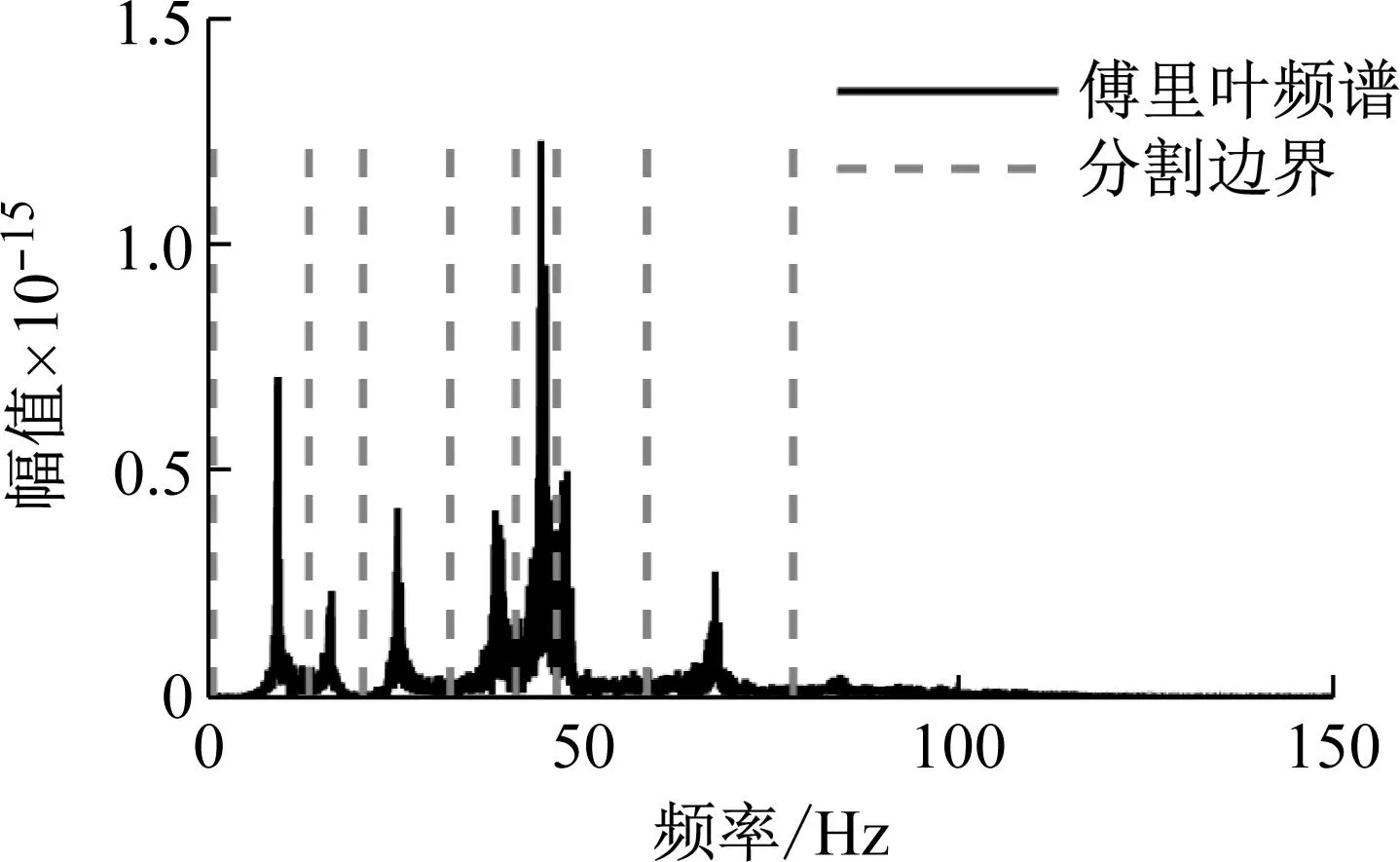
图12 傅里叶谱分割边界Fig.12 Segmentation boundaries of Fourier spectrum

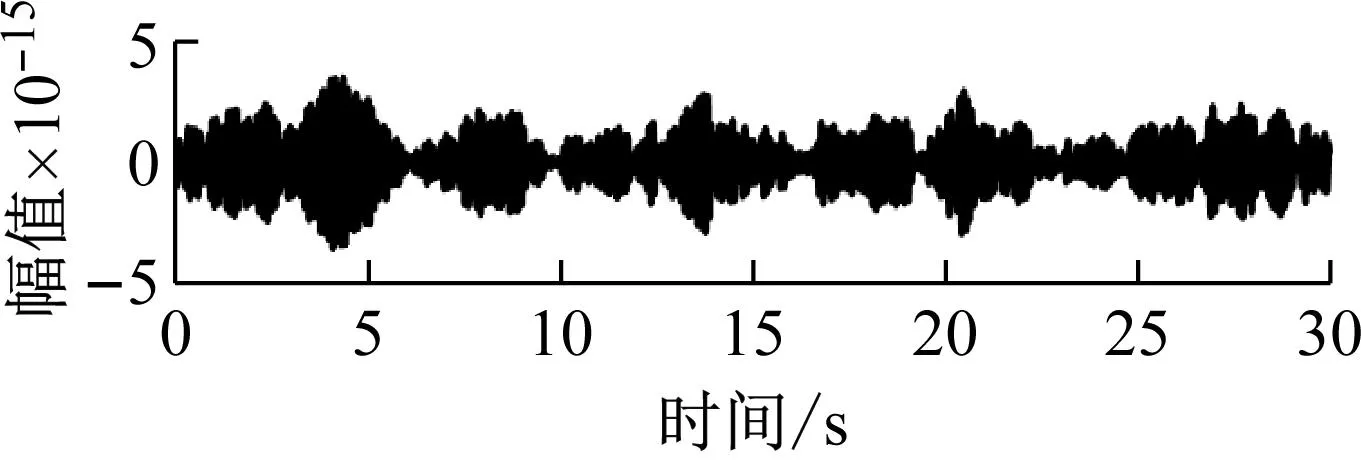
(a) 模态1

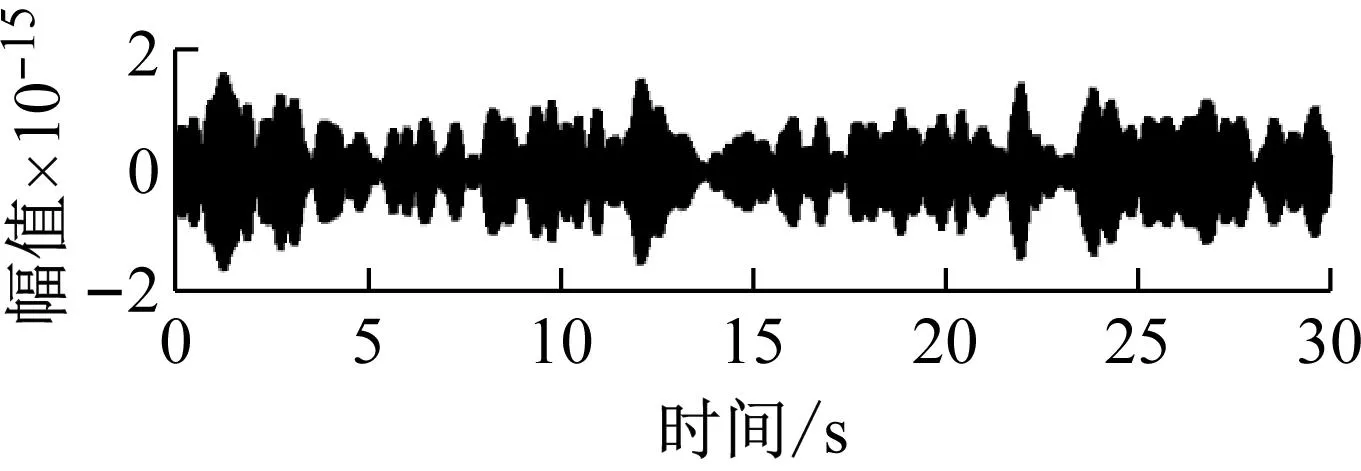
(b) 模态2

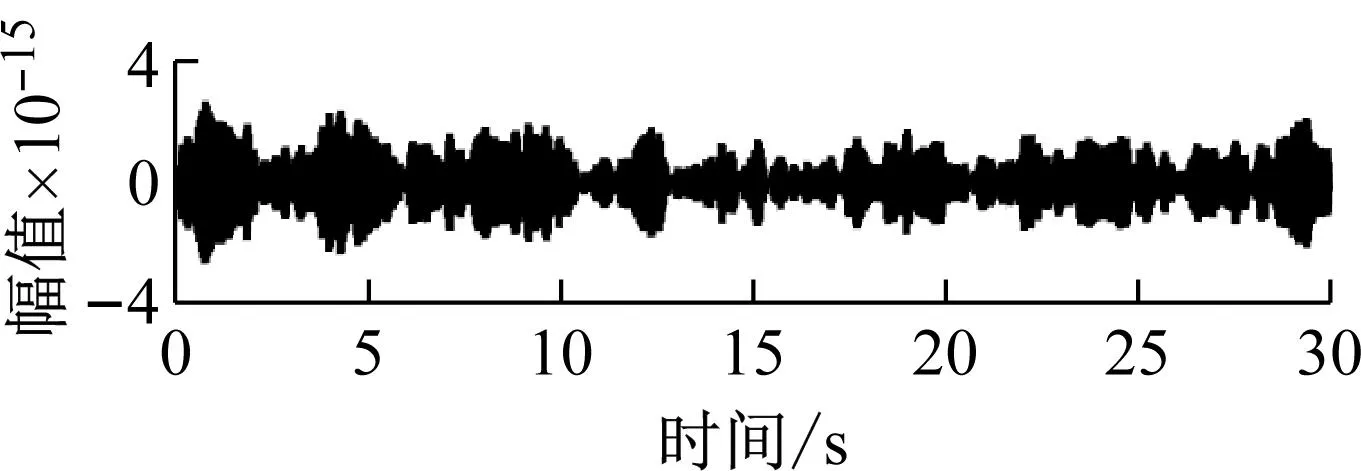
(c) 模态3图13 前三阶模态分量Fig.13 The first three modal components

采用RDT方法获取各阶模态分量的自由衰减响应信号,其中前三阶模态自由衰减响应如图14所示。结合HT获取幅值函数与相位函数,使用指数衰减拟合和直接求导方法得出各阶模态频率及阻尼比参数。

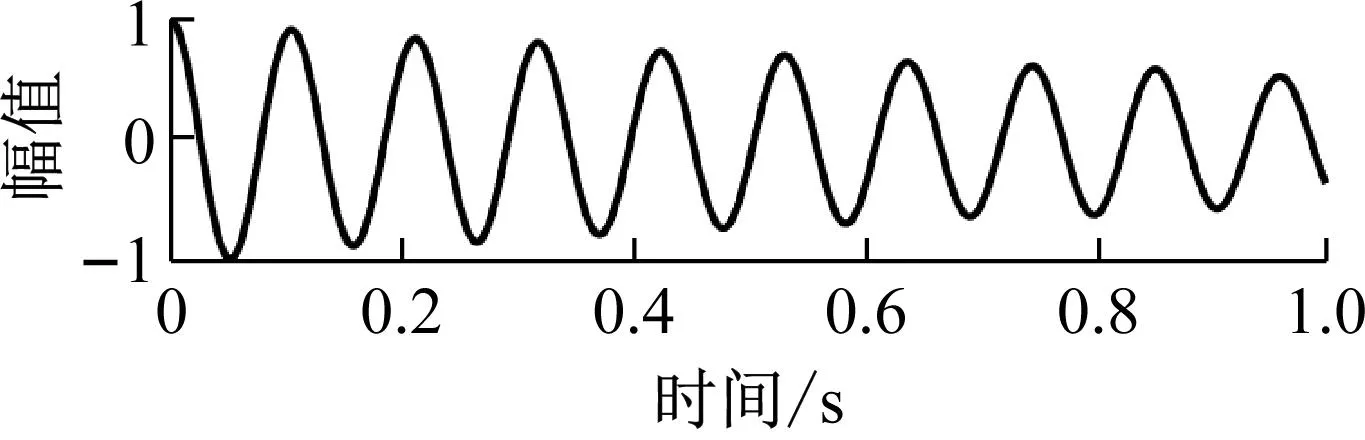
(a) 模态1

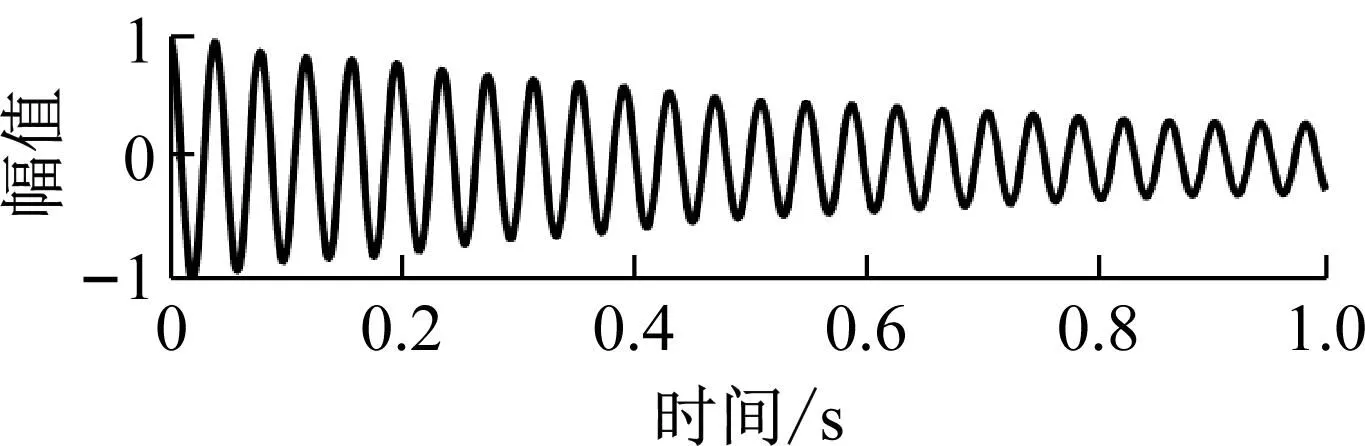
(c) 模态3图14 前三阶模态自由衰减响应Fig.14 Free attenuation response of the first three modals

为验证基于IEWT的模态参数识别方法的准确性,采用WT方法[5]及AR-EWT方法[8]进行横向对比,三种方法的模态参数识别结果汇总于表2中。为进一步评估各方法的模态参数识别精度,使用相对误差对各参数进行评估,如式(21)所示。

(21)

式中:Er为相对误差;x为识别值;X为理论值。

由表2可知,对比WT方法与AR-EWT方法,IEWT方法能够全部准确识别出各阶模态的频率及阻尼比信息。对于固有频率,IEWT方法的相对误差小于1.40%,与理论值基本一致;对于阻尼比,IEWT方法对于前两阶的识别精度较高,且阻尼比识别与理论值较为接近。

3 基于IEWT的海洋平台结构模态参数识别

为验证在实际应用中的可行性,选用实验室自升式海洋平台模型为研究对象,基于IEWT方法对其进行模态参数识别。

3.1 数据采集

该海洋平台模型基于某自升式海洋平台,以1∶40比例几何缩放而成,整体结构由三个桁架桩腿和甲板组成,如图15所示。甲板上布置6个加速度传感器,其中1#、3#、5#传感器对应x方向,2#、4#、6#传感器对应y方向,传感器布置位置如图16所示。

图15 海洋平台模型Fig.15 Offshore platform model

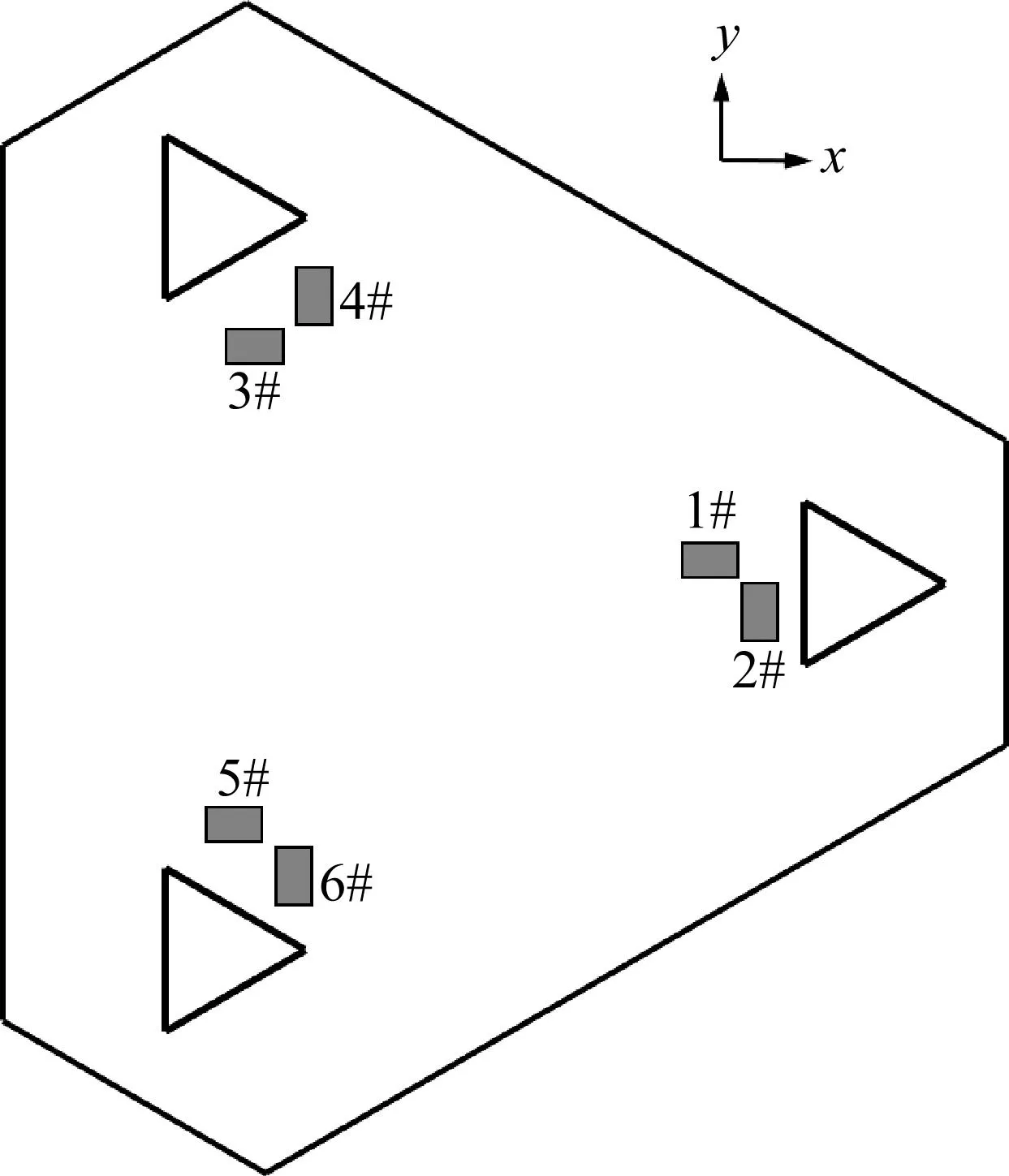
图16 传感器布置图Fig.16 Layout of acceleration sensors

传感器选用891-2型低频拾振器,数据采集设备选用cDAQ-9189机箱与NI 9231采集卡,采样频率为400 Hz。

3.2 模态参数识别

选取x方向传感器数据进行分析,数据截取时长为60 s,其中1#传感器数据如图17所示。

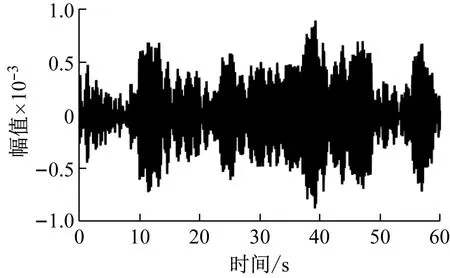
图17 1#传感器数据时程图Fig.17 Time history chart of sensor 1 data

基于IEWT方法获取该信号的奇异值的分割边界,如图18所示。奇异值谱被划分为5个频谱区间,其中第1、5个频谱区间为噪声,对第2、3、4频谱区间为模态区间。

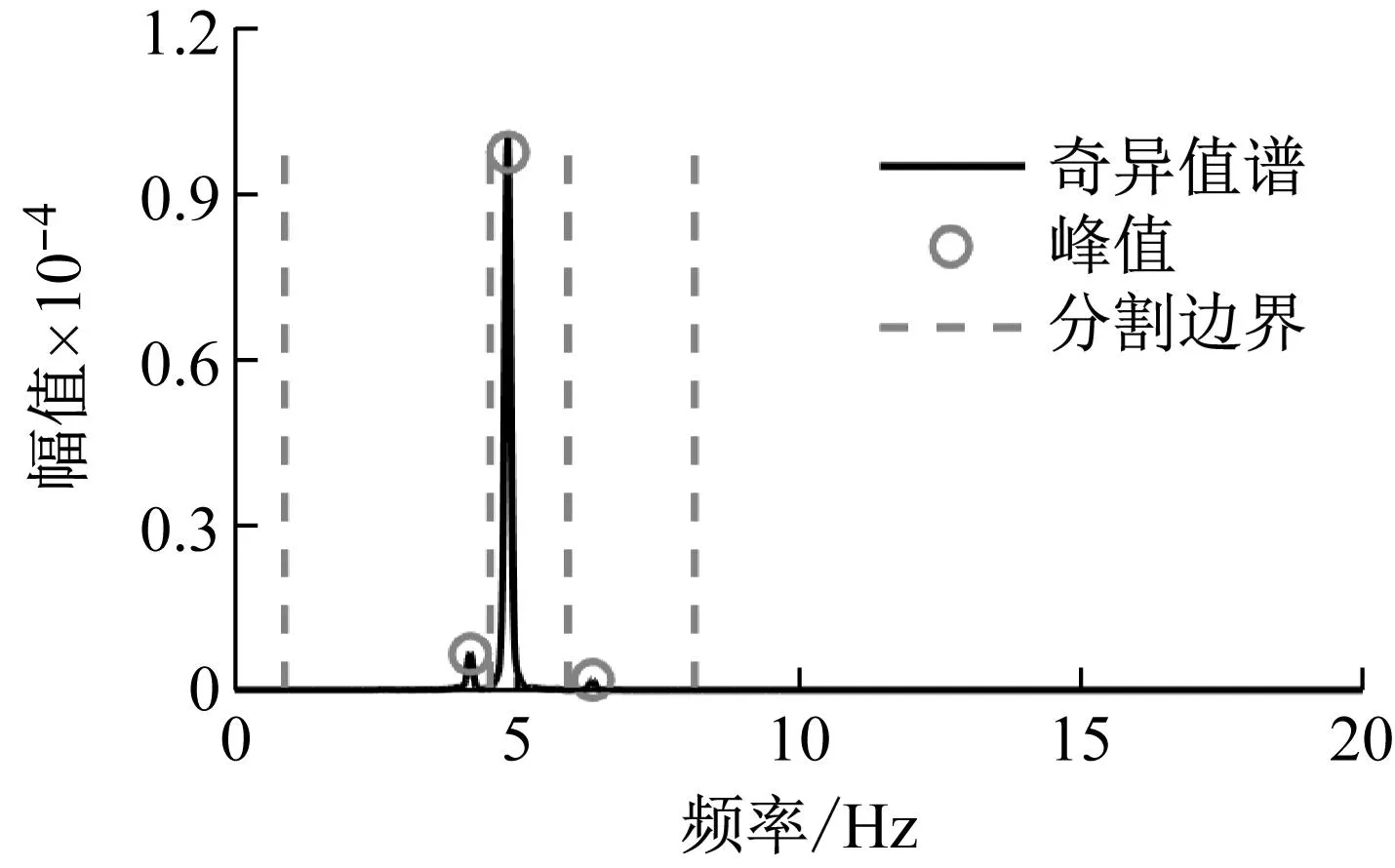
图18 奇异值谱及分割边界Fig.18 Fourier spectrum and boundaries

将奇异值谱中的分割边界映射至傅里叶频谱中,如图19所示。构造小波滤波器组进行频谱分割,获得三个模态分量,结合RDT及HT方法计算各阶模态频率及阻尼比,如表3所示。

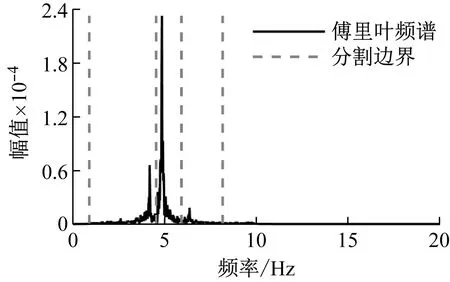
图19 傅里叶谱分割边界Fig.19 Segmentation boundaries of Fourier spectrum

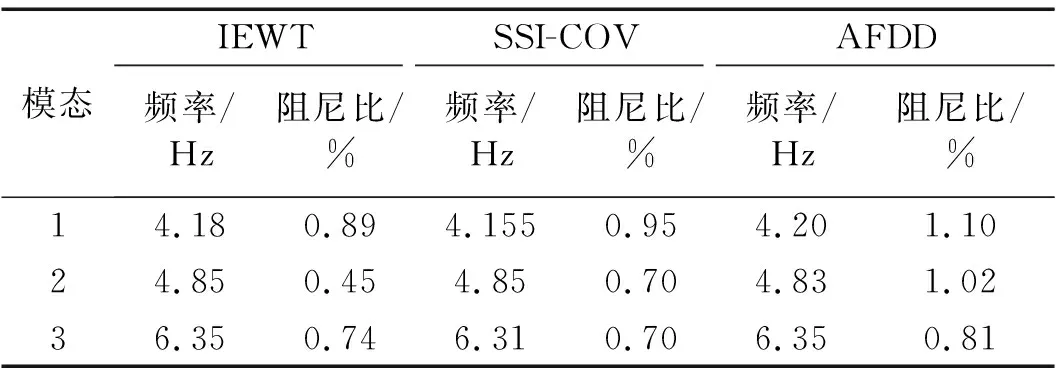
表3 模态参数识别结果Tab.3 Modal parameter identification results

由表3可知,IEWT方法成功识别出了前三阶模态,其中模态频率分别为4.18 Hz、4.85 Hz、6.35 Hz。为验证该方法识别结果的可靠性,使用基于协方差的随机子空间(stochastic subspace identification-covariance, SSI-COV)方法和自动频域分解(automated frequency domain decomposition, AFDD)方法进行对比,不难发现,三种方法对于模态频率的识别结果较为接近,也验证了IEWT方法在实际应用中的可靠性。

海洋平台等大型结构进行模态分析时,通常在环境激励下进行,由于这种分析方法不会中断结构的正常运营,又称工作模态分析。在对结构进行工作模态分析时,结构阻尼比的识别结果会受到环境振动水平及分析时长的影响,具有一定的离散性[16]。目前大型结构的阻尼机理不明确,在低水平环境振动下增大采样时长能够降低阻尼比识别结果的离散性,而实际的海洋平台环境激励较为复杂,难以控制。相较于阻尼比,结构的模态频率识别精度较高、离散性较低、可靠性强,可以作为结构的损伤指标。

此外,与SSI-COV等方法相比,IEWT具有较快的运算速度,完成60 s时长数据的模态参数识别用时仅为0.51 s,因此该方法在结构健康监测中具有较好的应用价值,可用于结构模态参数自动识别,为后续的结构损伤预警及损伤评估提供依据。

4 结 论

针对EWT算法在含噪信号傅里叶频谱中分割边界容易误判的缺陷,本文利用奇异值谱在处理含噪信号中的优势,结合尺度空间算法实现分割边界的自适应划分,对EWT算法进行改进。通过自由振动响应信号、Benchmark模型信号与自升式平台模型实测信号对算法进行验证,得到以下结论:

(1) 基于奇异值谱和尺度空间算法,对EWT算法进行改进,提出一种能够实现模态参数自动识别的IEWT方法。

(2) 通过将IEWT方法应用于三自由度的自由振动响应信号和Benchmark模型信号,并分别与EWT、WT、AR-EWT方法进行对比,结果表明IEWT方法能够实现频谱的自适应划分和模态参数的准确识别。

(3) 基于室内自升式海洋平台模型,将IEWT方法应用到实际数据的模态参数识别中,对比SSI-COV及AFDD方法的识别结果,结果表明IEWT方法在实际应用中具有可靠性强、计算速度快的优点,在其他大型工程结构健康监测中具有一定的推广应用价值。