基于微分法的大跨度桥梁三维颤振敏感性分析

翁祥颖, 董 锐, 葛耀君

(1. 福建理工大学 福建省土木工程新技术与信息化重点实验室, 福州 350118;2. 福州大学 土木工程学院, 福州 350118; 3. 同济大学 土木工程防灾减灾国家重点实验室, 上海 200092)

桥梁颤振是一种灾难性的桥梁风致失稳破坏形式,在设计阶段提升大跨度桥梁的颤振性能对桥梁结构的安全性和经济性具有重要意义。为此,研究人员开展了大量的研究工作,不断探究桥梁结构动力特性和气动外形等设计参数对桥梁颤振性能的影响规律,以期深入了解桥梁颤振机理,为工程实践提供更加有效的指导和支撑。

在大跨度桥梁设计阶段,设计人员需要快速准确地预测桥梁颤振性能对设计变量的响应,从而提出具有理想颤振性能的设计方案。上述各种方法揭示了各类设计参数对桥梁颤振性能的影响规律,但对于设计人员而言,这些方法的实现或应用门槛相对较高,在初步设计阶段的桥梁气动选型时,仍需要花费较大的时间和人力成本。

敏感性指标反映了设计参数变化对系统输出的影响程度,广泛应用于航空、车辆、造船等工业设计过程。敏感性分析常采用有限差分法、直接微分法等手段,其原理简单,计算速度快,尤其适用于设计阶段帮助设计人员快速掌握相关参数变化对桥梁结构颤振性能的影响规律。目前常用的桥梁颤振敏感性分析方法主要是依托于参数化分析的有限差分法,其原理简单,但是随着设计变量增多,该方法将面临计算成本和时间成本问题。此外,有限差分法对数值噪声敏感,要求数值计算精度较高,无疑进一步增加了相关成本。与有限差分法相比,直接微分法计算效率高、计算结果准确,且通用性更强。受限于桥梁颤振相关变量之间复杂的依赖关系,尤其是颤振导数对风速的隐式依赖关系,采用直接微分法研究桥梁颤振敏感性的相关报道较少。

本文从特征值问题敏感性出发,利用桥梁颤振状态矩阵的左右特征向量正交特性,构建了在设计参数小幅摄动时桥梁多模态耦合颤振规格化条件,结合桥梁颤振临界条件,得到了桥梁三维耦合颤振系统的特征值及颤振临界风速对设计参数的敏感性表达式。通过对比有限差分法和参数化计算得到的理想平板断面简支梁桥颤振敏感性,检验本文方法的准确性和高效性。针对一座主跨918 m的悬索桥,运用本文方法研究结构参数和气动参数对桥梁颤振性能的影响规律。本文的研究工作有助于精确且高效地量化相关设计参数对桥梁颤振性能的影响规律,为设计阶段桥梁高效地开展气动选型提供技术支撑。

1 桥梁三维颤振局部敏感性分析方法

以Scanlan[10]自激力模型表述的桥梁三维颤振运动方程为

(1)

式中:M、C和K分别为桥梁结构的模态质量、阻尼和刚度矩阵;列向量q为模态参与向量;ρ为空气密度;B为桥面宽度;U为来流风速;As和Ad分别为广义气动刚度和气动阻尼矩阵。

(2)

(3)

(4)

(5)

式是:K=Bω/U为折算频率;Φ为桥梁模态振型矩阵;diag(*)表示以*为元素的对角矩阵;上标T表示转置运算。

1.1 有限差分法

有限差分法是最简单的敏感性分析方法,通过假定被研究的参数发生小幅扰动,利用差分计算近似得到参数的敏感性。前向差分和中心差分是两种最常用的差分格式,以前向差分为例,其计算过程如下

(6)

式中:r为目标函数;t、θ为变量;Δθ为相对于θ0的小幅扰动。有限差分法用于敏感性分析时具有简单、灵活及通用性强的优点。

以参数化计算为基础,有限差分法常用于研究桥梁结构的动力特性、气动外形、气动导数等参数对桥梁颤振临界风速的影响规律[11-14]。由于有限差分结果对噪声及误差敏感,因此这类研究对计算或模拟过程的精度要求较高,当需要研究的参数数量众多时,有限差分法将需要较高的实施成本。

1.2 微分法

将式(1)扩展为状态空间形式[15]

(7)

其中

记风速U处系统矩阵A的特征值和特征向量分别为Λ和Γ,即特征值λi=-ξiωi±iωi对应于特征向量

(8)

易知λi为式(1)的复特征值,而ψi则为式(1)右特征向量。

假定桥梁颤振影响因子β,则系统的特征值、特征向量、颤振临界风速及系统矩阵均为β的函数。对于自激力作用下的桥梁结构第i阶模态,有

P(λi(β),Uc(β),β)ψi(β)=0

(9)

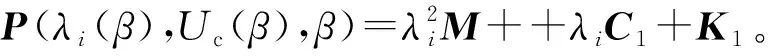
系统矩阵A的左特征向量Π满足

ΛΠT=ΠTA

(10)

其中

由式(10)可得桥梁结构的第j阶模态满足

(11)

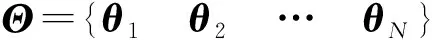
(12)

(13)

文献[16]对模态正交条件采用Taylor展开获取模态规格化条件,此处对式(13)同样采用Taylor展开,并减去式(12)后可得

(14)

对第i阶模态,式(14)中i=j,括号内的表达式简化为∂P/∂β|λ=λi,取左右特征向量使其满足规格化条件

(15)

考虑影响因子β对系统的影响,对i阶模态振动方程式(9)求β的导数

(16)

(17)

当系统处于颤振临界状态时,发散模态的特征值实部Re(λi)=0,因此对于桥梁颤振发散模态有如下实部和虚部方程

(18)

(19)

式中,Re()、lm()分别表示复数的虚部和实部。联合求解式(18)、式(19)便可得敏感性dUc/dβ及dωi/dβ。

式(18)和(19)联合求解时,发现Scanlan自激力模型是U的隐函数,无法直接求解∂P/∂Uc。风洞试验表明,U通过颤振导数改变系统状态,即系统矩阵A是U的函数,为求得∂P/∂Uc引进工程上常用的Roger有理函数近似颤振自激力,即

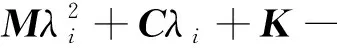
(20)

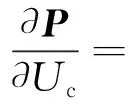
(21)

2 结构参数影响

影响桥梁颤振临界风速的结构参数主要包括模态质量、阻尼比和固有频率。由式(9)有

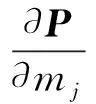
(22)

(23)

(24)

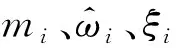
3 气动参数影响

基于桥梁有限元模型,求广义气动刚度和气动阻尼矩阵的偏导数∂As/∂β、∂Ad/∂β

(25)

(26)

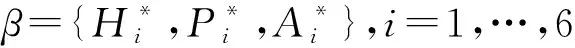
4 大跨度桥梁三维颤振敏感性分析

本章首先针对经典薄平板简支梁桥[17]开展三维颤振敏感性分析,对比有限差分法及参数化分析方法,以评估本文方法的精度和效率。在此基础上,针对一座主跨918 m的双塔三跨悬索桥开展颤振敏感性分析,研究桥梁结构参数和气动参数对实桥颤振性能的影响规律。

4.1 理想薄平板简支梁桥三维颤振敏感性分析

具有薄平板断面的简支梁桥结构参数如表1所示。选取前10阶模态进行多模态耦合颤振分析,相关模态特性如表2所示。

表1 理想薄平板简支梁结构参数Tab.1 Structural characteristics of the simple supported beam with an ideal thin flat section

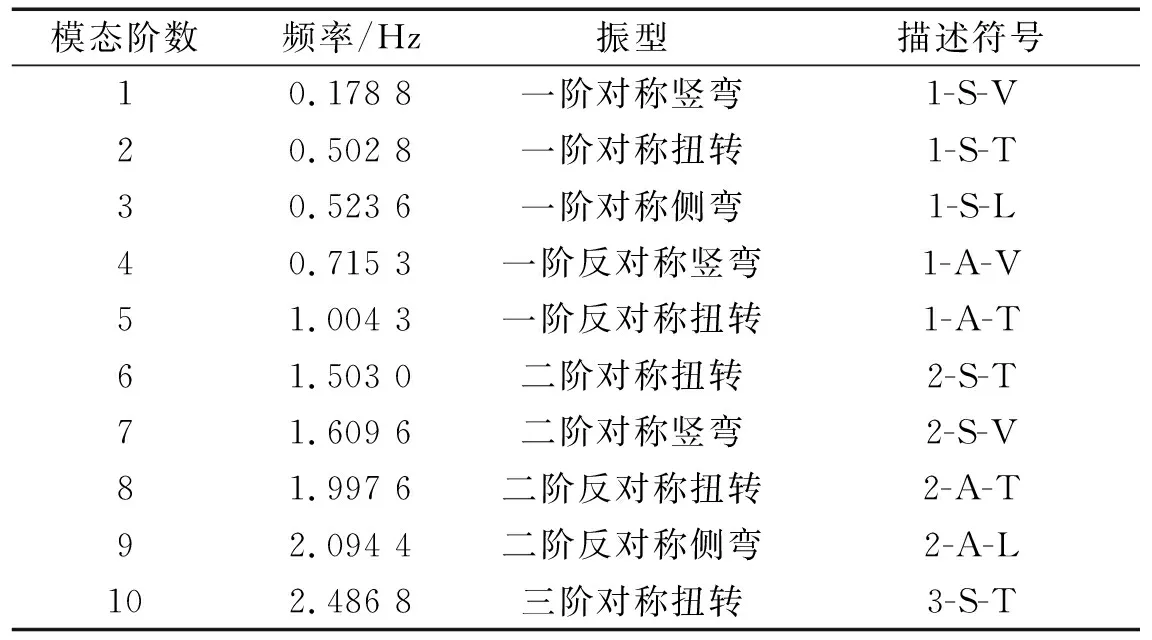
表2 简支梁前10阶模态振型特性Tab.2 Modal characteristics of the first 10 modes of the simple supported beam

薄平板断面的颤振导数由Theodorsen函数及准定常准则确定[18]。

多模态耦合颤振计算结果表明简支梁的颤振临界风速为143.9 m/s,与文献[17]的研究结果吻合。在迭代过程中,对于每一级风速Ui均计算系统特征值的敏感性,用于预测下一级迭代风速Ui+1对应的系统振动频率和阻尼比,预测结果与数值迭代结果对比如图1所示,图中实线代表数值迭代结果,散点表示预测结果,表明二者吻合较好。

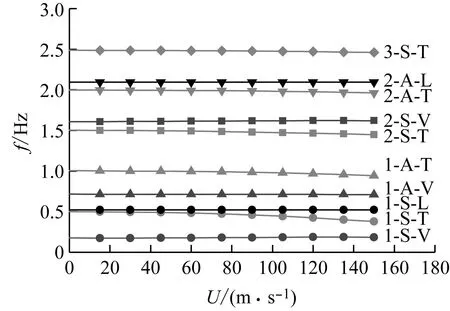
(a) 振动频率

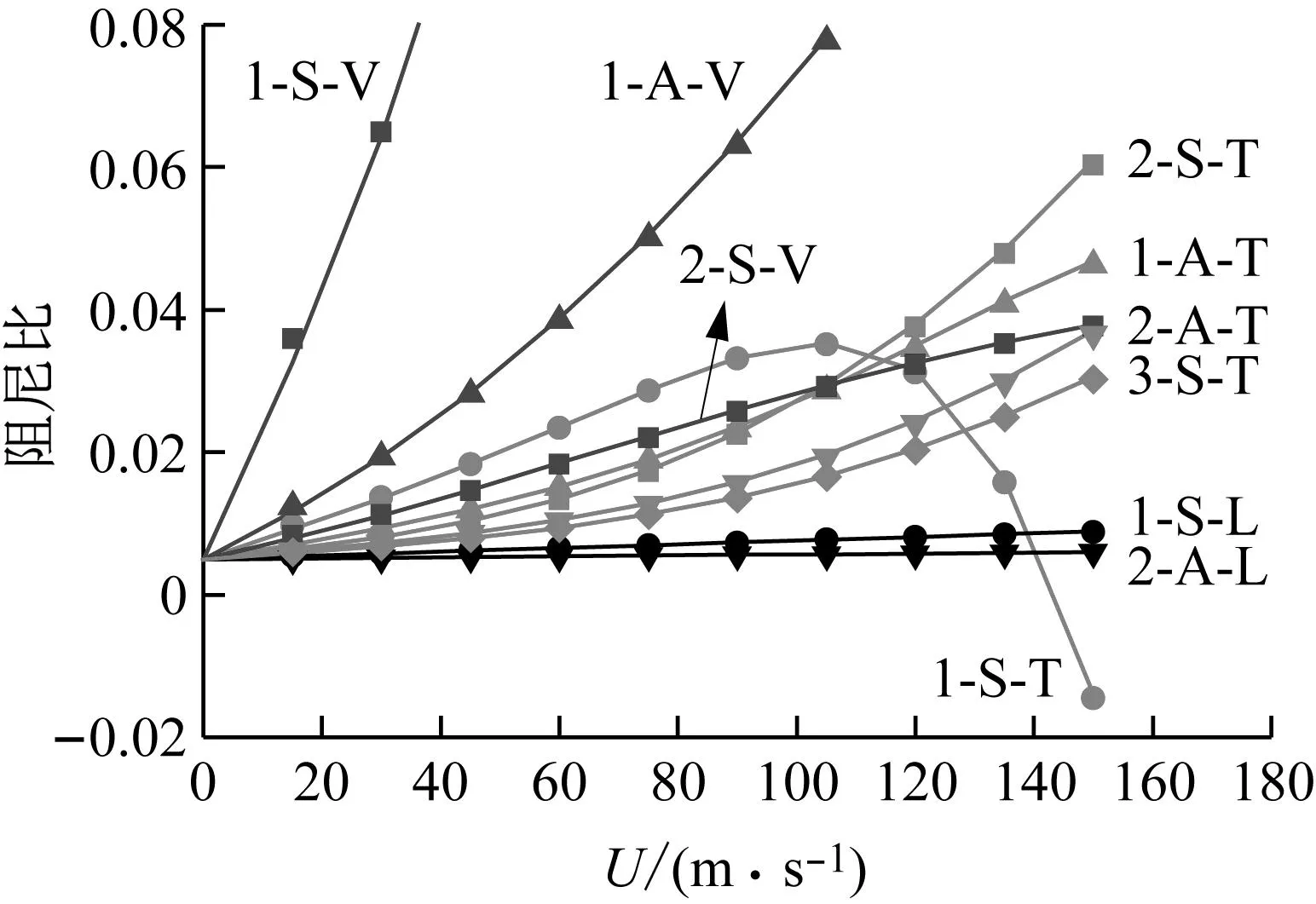
(b) 阻尼比图1 简支梁颤振分析结果比较Fig.1 Comparison of flutter analysis of ratios of the simple supported bridge

图2给出了颤振临界风速对各阶模态参数的敏感性dUc/dβi,横坐标表示模态阶数,dUc/dβi>0表示增大参数βi将提高颤振临界风速Uc,反之dUc/dβi<0则表示增大βi将降低颤振临界风速Uc。由图2可知简支梁的颤振临界风速主要对1-S-V和1-S-T的模态参数敏感,而其它模态的参数变化对Uc的影响十分微弱。结合图1(b)可知,1-S-T为简支梁的颤振发散分支,图2表明颤振临界风速对1-S-T的3个模态参数的敏感性均大于1-S-V对应的模态参数,即该简支梁的颤振发散分支1-S-T的模态参数对桥梁颤振的影响最显著。此外,颤振临界风速对阻尼比最敏感,对模态频率和模态质量的敏感性则大致基本相当。由dUc/dβi的符号可知,增大各模态的阻尼比和模态质量均会提高颤振临界风速。各模态频率对颤振临界风速的影响则不一致,增大一阶扭转频率将提高颤振临界风速,而增大一阶竖弯频率则导致颤振临界风速降低。综合竖弯和扭转频率的影响来看,增大基础扭弯频率比将提高颤振临界风速。

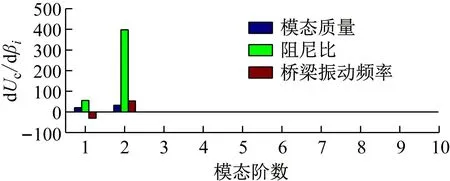
图2 简支梁颤振临界风速对结构模态参数的敏感性Fig.2 Sensitivities of critical flutter wind speed with respect to the simple supported beam modal dynamic characteristics

基于简支梁结构参数敏感性,可预测相关模态参数发生一定变化时简支梁的颤振临界风速。表3对比了本文微分法预测结果和有限差分法、参数化分析方法的计算结果,表明当模态质量和频率的变化幅度在±5%的范围内、结构阻尼比的变化范围在0～200%时,本文微分法预测结果与有限差分法及参数化分析结果均吻合较好。

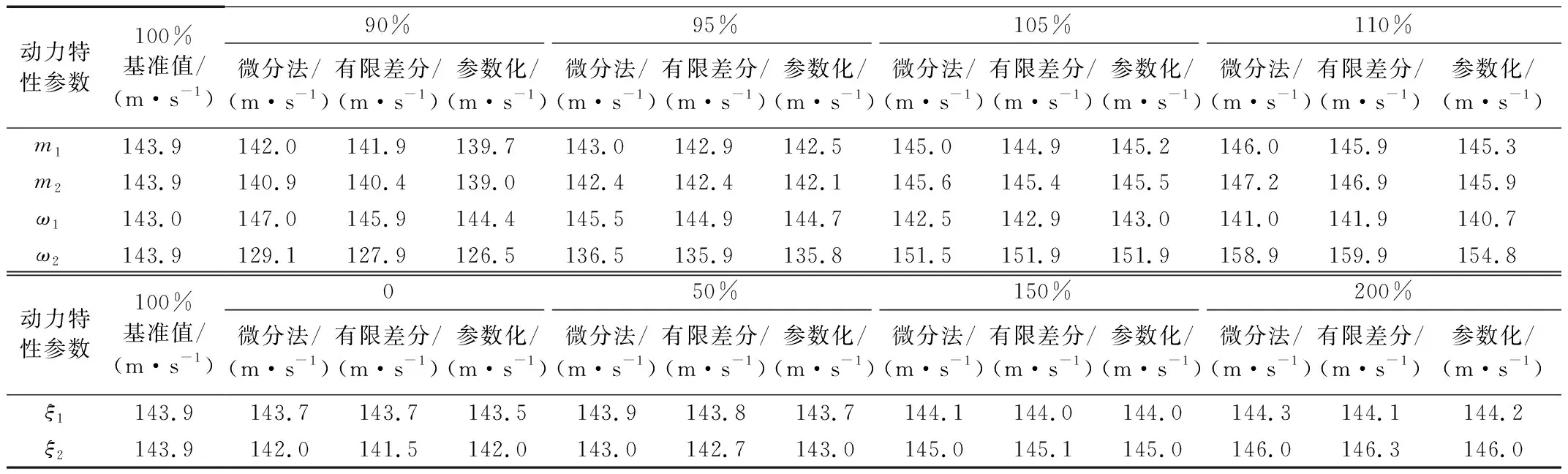
表3 模态参数小幅摄动时简支梁颤振临界风速Tab.3 Critical flutter wind speed of simple supported beam with perturbed modal characteristics

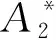
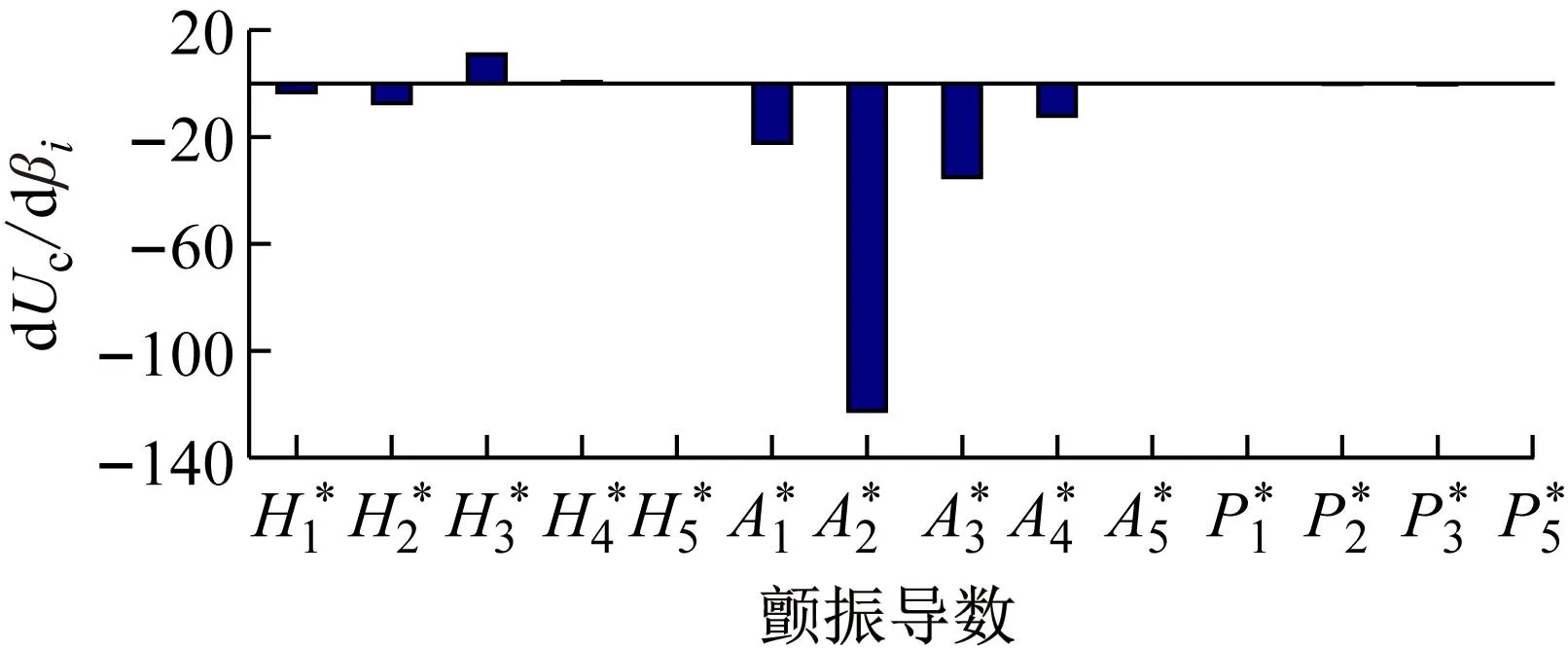
图3 简支梁颤振临界风速对颤振导数的敏感性Fig.3 Sensitivity of critical flutter speed with respect to simple supported beam flutter derivatives

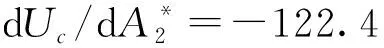
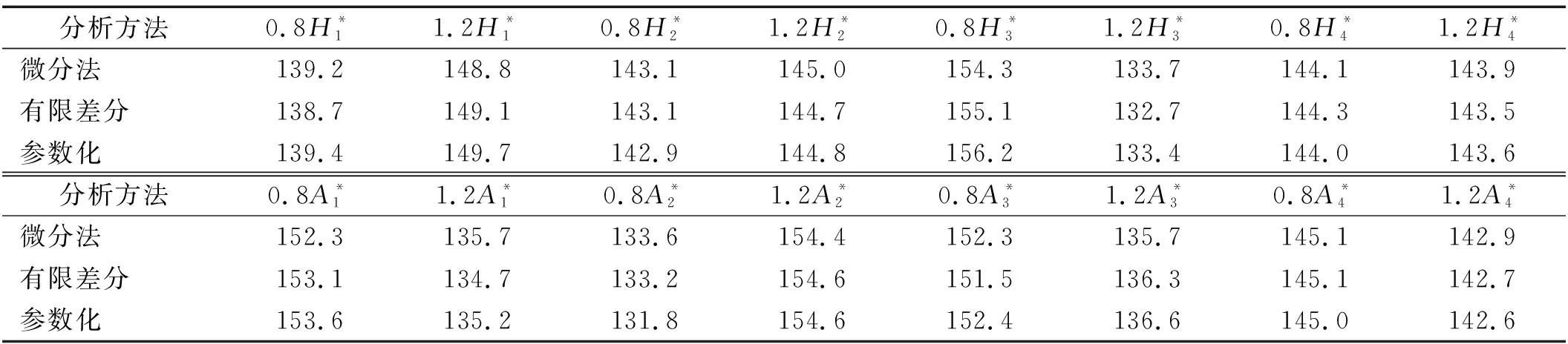
表4 颤振导数摄动时简支梁颤振临界风速Tab.4 Critical flutter wind speed of simple supported beam with perturbed flutter derivatives 单位:m/s

为对比本文微分法和有限差分法进行敏感性分析的计算效率,分别统计了两种方法进行简支梁颤振敏感性分析的计算耗时,如表5所示。分析所用的计算机配置为i7-8560U CPU、16 GB内存。考虑到计算机系统因素对单次计算时间可能造成浮动的现象,表中所给的计算时间均为10次分析的平均计算时间。

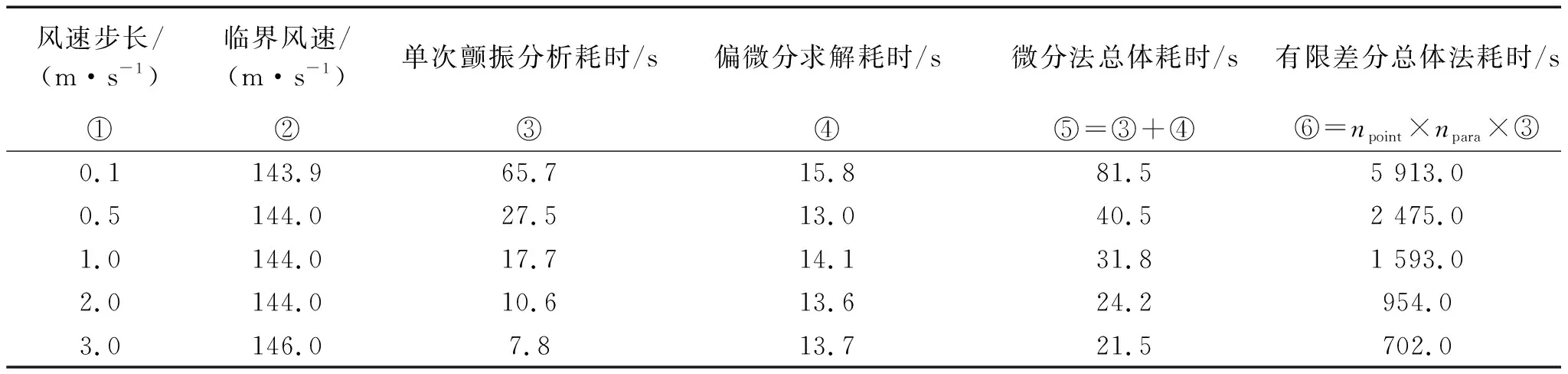
表5 简支梁颤振敏感度分析耗时Tab.5 Time consumed by flutter sensitivity analysis of simple supported beam

表5中:第⑤栏为采用本文微分法分析简支梁所有结构参数和气动参数敏感性所需时间。第⑥栏中npoint为单个参数采用有限差分法计算敏感性需要参数化计算的次数,由式(6)可知,采用一阶前向差分格式计算每个参数的敏感性时npoint取2;npara为待研究的参数数量,本例共有45个,其中10阶模态共30个结构参数,非零气动参数15个。

表5的⑤和⑥两栏对比结果表明,当选取合适的风速步长时,本文微分法的平均计算时间显著小于有限差分法。分析可知,微分法只需要一次颤振分析和一次偏微分求解便能得到所有参数的敏感性;而有限差分法需要进行两次参数化运算才能得到一个参数的敏感性,由此导致其在处理多模态耦合的桥梁颤振系统时,由于有较多的结构模态参数需要评估,导致有限差分法相对于本文微分法存在计算成本和时间成本劣势。

4.2 大跨度悬索桥三维耦合颤振敏感性分析

以图4所示的双塔三跨纵向全漂浮悬索桥为研究对象,该桥跨径布置为264+918+365=1 547 m,主梁采用图5所示的扁平钢箱梁,相关结构参数如表6所示。通过有限元分析获取该桥的动力特性,选取对耦合颤振有较大影响的8阶模态进行颤振敏感性分析,相关模态动力特性如表7所示。

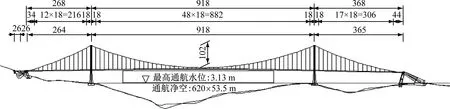
图4 悬索桥跨径布置Fig.4 Schematic description of the suspension bridge

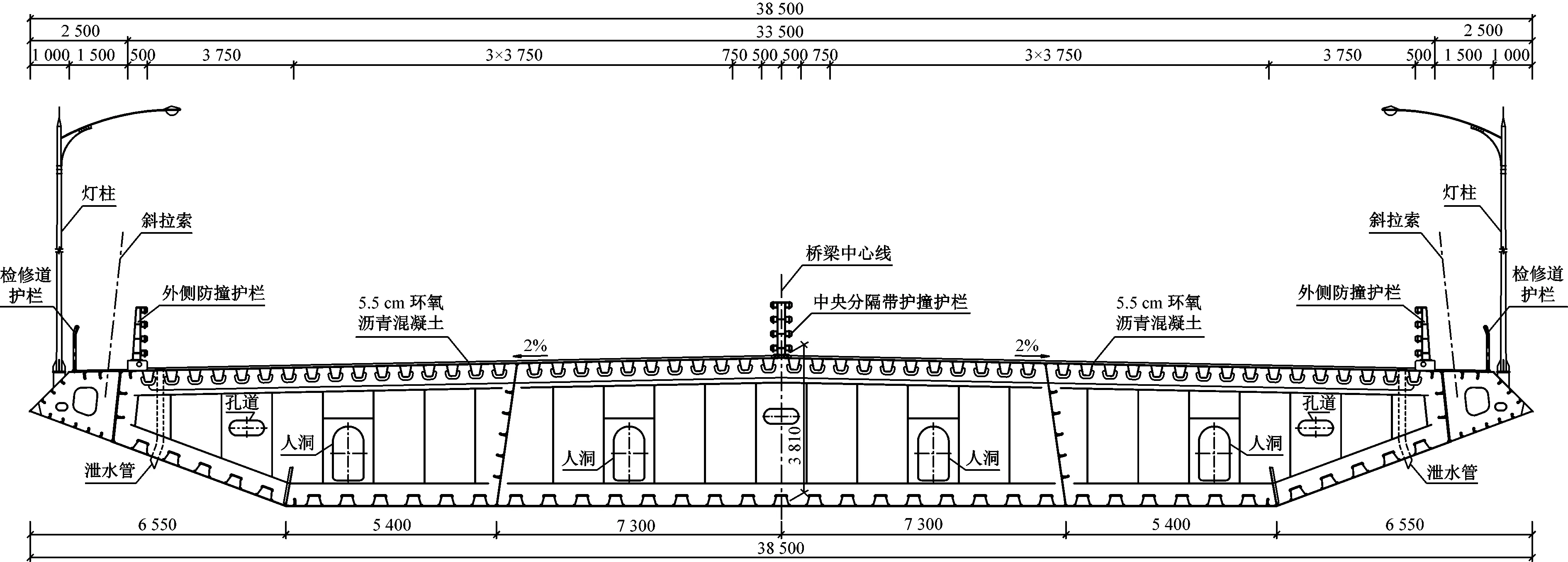
图5 成桥状态加劲梁断面图Fig.5 Cross section of the stiffening girder in operation periods

表6 加劲梁截面主要参数Tab.6 Sectional parameters of the stiffening girder

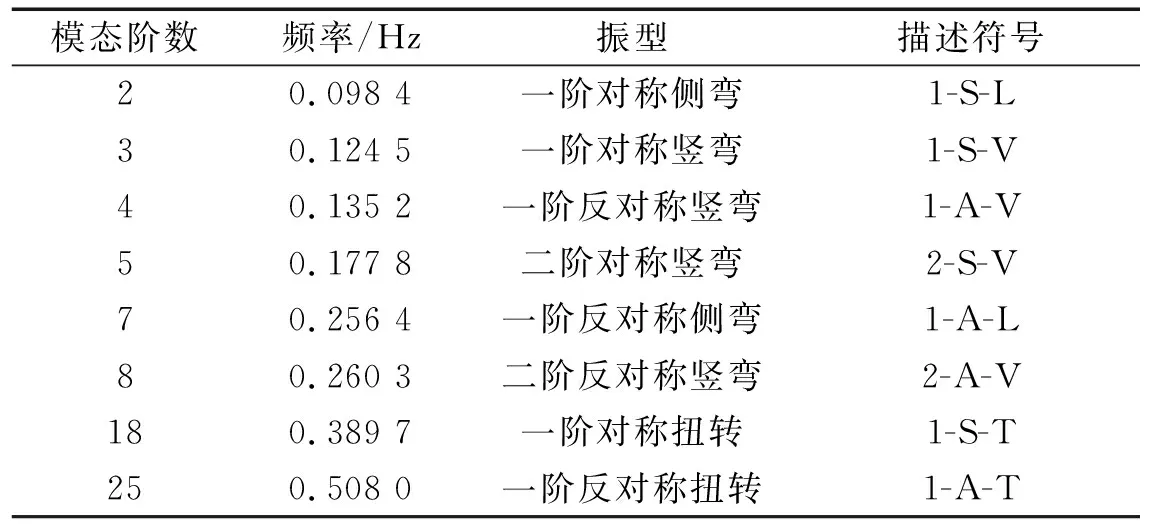
表7 参与耦合颤振分析模态Tab.7 Selected modes to participate coupled flutter analysis

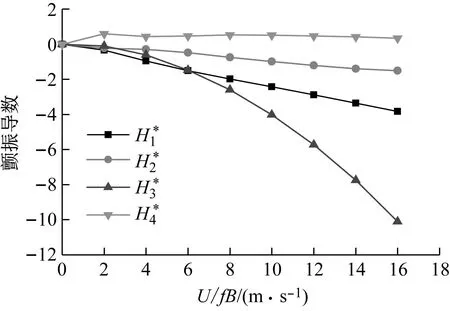
(a) 颤振导数

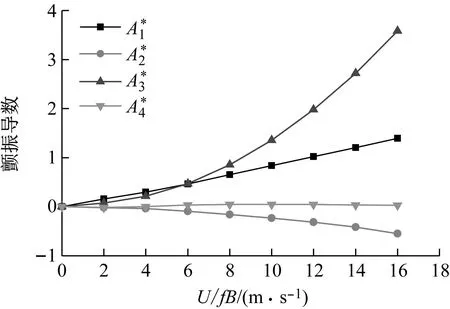
(b) 颤振导数图6 加劲梁断面颤振导数Fig.6 Flutter derivatives of the stiffening girder section

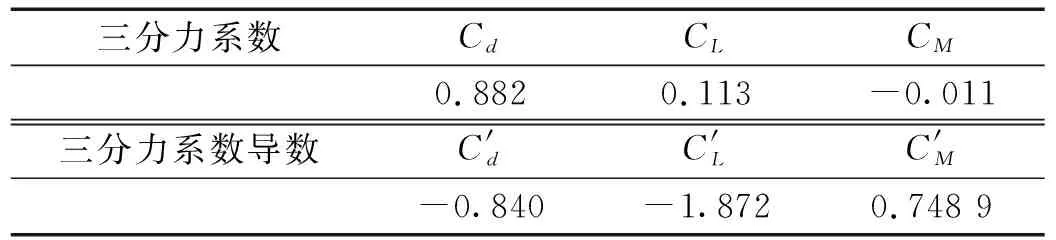
表8 加劲梁0°攻角三分力系数及其导数Tab.8 Force coefficients and their derivatives

该桥的耦合颤振分析结果如图7所示。颤振临界风速为85 m/s,颤振发散分支为1-S-T模态,对应于弯扭耦合扭转分支颤振发散,基于特征值敏感性式(17)预测的各阶模态阻尼比和振动频率与数值迭代结果吻合较好。

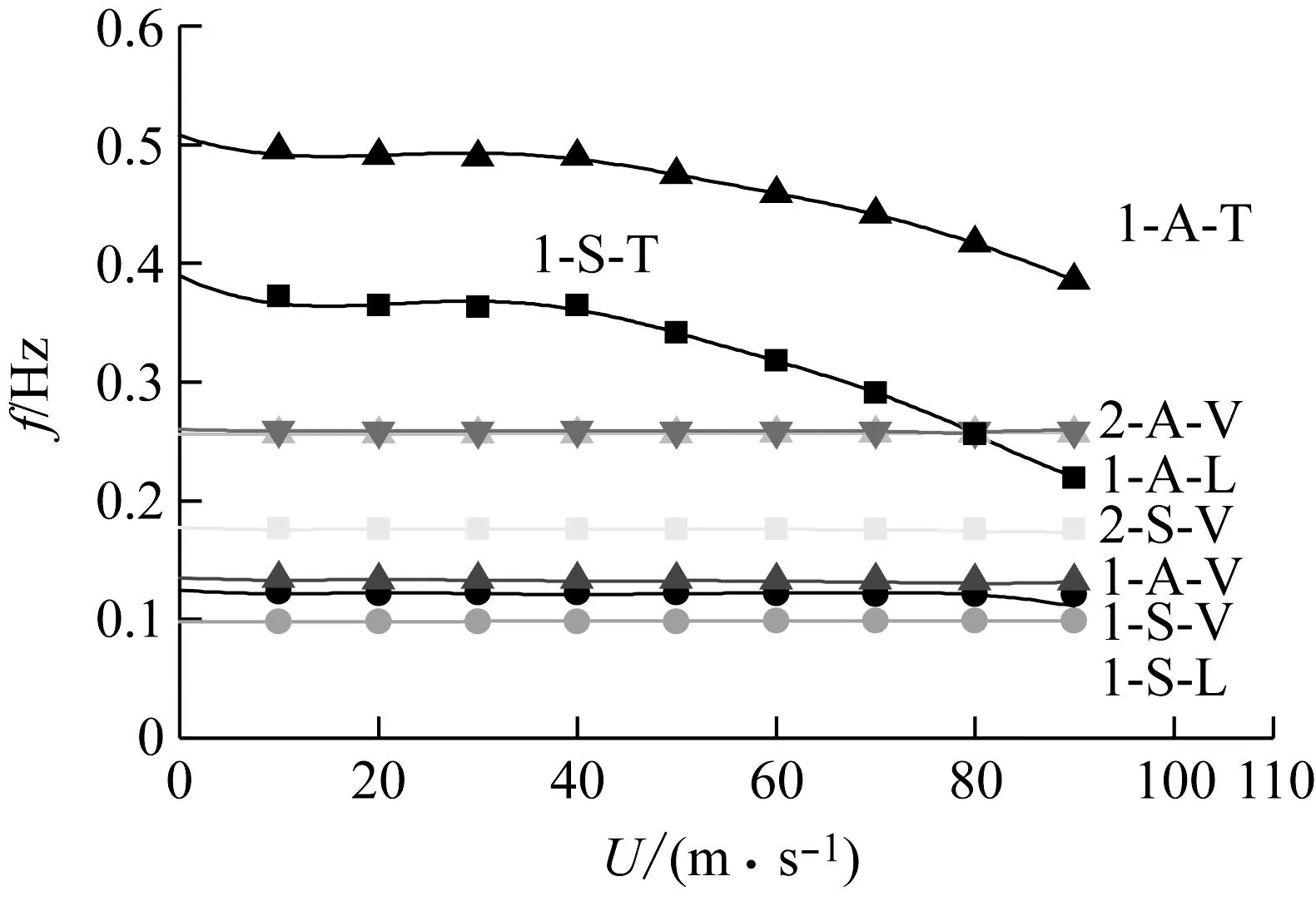
(a) 振动频率

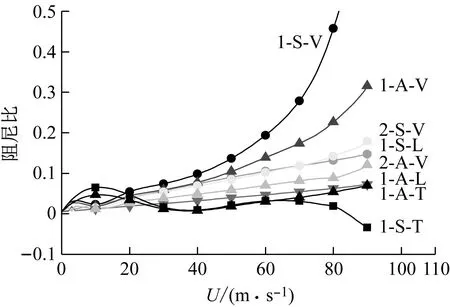
b) 阻尼比图7 悬索桥颤振分析结果比较Fig.7 Comparison of flutter analysis of ratios of the suspension bridge

图8给出了该桥颤振临界风速对各阶模态参数的敏感性。对比图2所示的简支梁敏感性,两桥的主导模态参数均为1-S-V和1-S-T模态参数,其中扭转发散分支1-S-T模态参数的影响更突出;不同的是,该桥的1-A-V和2-S-V模态的动力特性参数对颤振临界风速也有较大影响,表明该桥的模态耦合程度大于前述的简支梁桥。各组模态参数按敏感性由高到低排序依次为阻尼比、模态频率、模态质量。图8的敏感性数值表明,增大阻尼比、模态质量及基础扭弯频率比均会提高颤振临界风速。

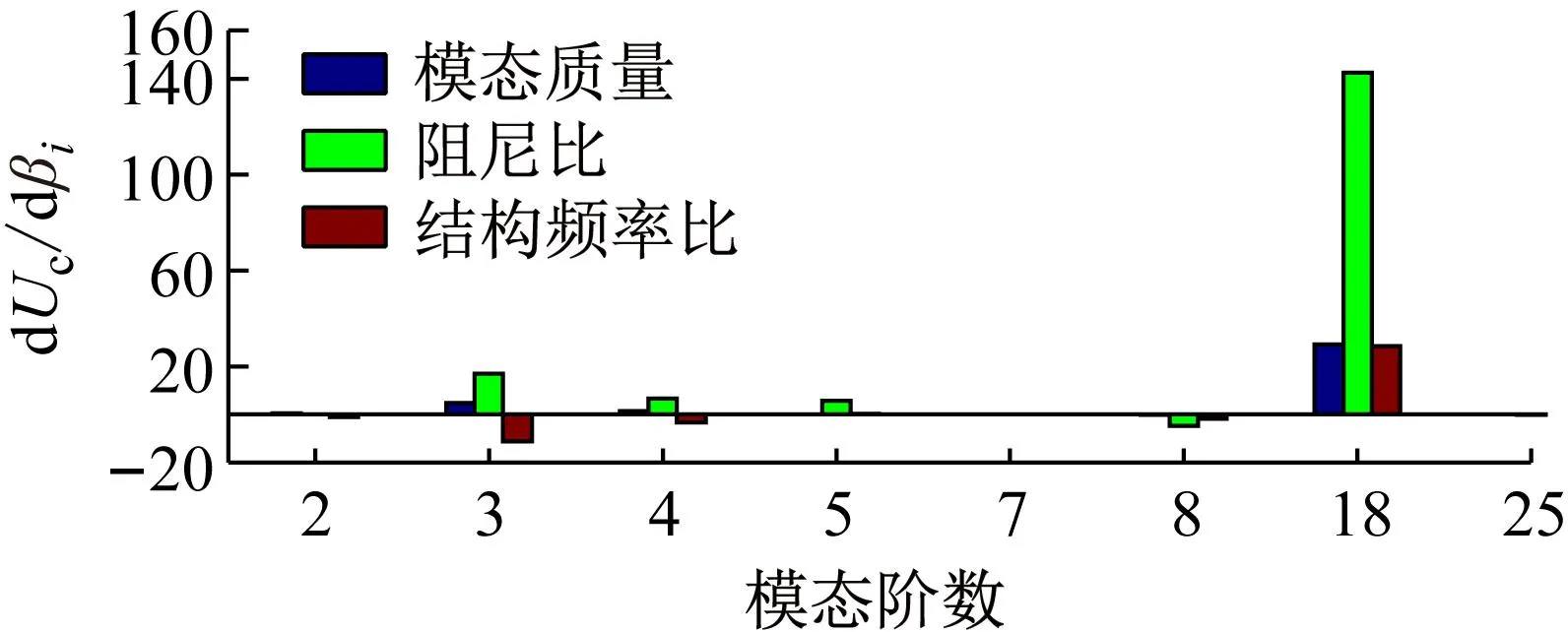
图8 悬索桥颤振临界风速对结构模态参数的敏感性Fig.8 Sensitivities of critical flutter wind speed with respect to the suspension bridge modal dynamic characteristics

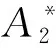
图9 悬索桥颤振临界风速对颤振导数的敏感性Fig.9 Sensitivity of critical flutter speed with respect to suspension bridge stiffening girder section flutter derivatives

5 结 论

本文基于直接微分法提出一种高效便捷的桥梁三维耦合颤振敏感性分析方法,旨在帮助设计人员在设计阶段高效精准地获取结构动力特性及颤振导数对大跨度桥梁颤振性能的影响规律。通过对理想平板断面的简支梁桥和采用流线型主梁断面的悬索桥颤振敏感性分析发现:

(1) 在参与三维耦合颤振分析的桥梁多阶模态中,颤振发散分支对应的模态参数对桥梁耦合颤振性能影响最大。对于采用理想薄平板、闭口钢箱梁等流线型断面的大跨度桥梁,一阶对称扭转模态的动力特性参数对桥梁的颤振临界风速的影响最显著,一阶对称竖弯次之,而其它阶模态参数的影响则相对较弱。

(2) 增大一阶竖弯和一阶扭转模态的模态质量,结构阻尼比及基础扭弯频率均能提高桥梁结构的颤振临界风速,但颤振临界风速对各模态参数的敏感性差异较大,按敏感性由高到低排序依次为阻尼比、模态频率和模态质量。