小净距隧道先行洞爆破开挖对后行洞围岩稳定性影响研究

李旭哲, 李文杰, 毕志刚, 梁 斌

(1.河南科技大学 土木建筑学院,河南 洛阳 471000; 2.中铁十五局集团第一工程有限公司,西安 710018)

随着我国交通系统的发展,小净距隧道的应用越来越广泛。由于小净距隧道左右洞之间距离较小,先行洞爆破施工时若产生较大的振动响应,易对中夹岩柱及后行洞围岩稳定性造成不利影响[1-2],因此开展隧道爆破开挖过程中振动响应分析具有十分重要的意义。

近年来,诸多学者针对小净距隧道爆破振动响应问题进行了大量研究,并取得了一定的成果。Shi等[3]采用量纲分析法研究了深埋小净距隧道爆破振动衰减规律,建立了考虑抵抗线和临空面的萨多夫斯基扩展公式。蒙国往等[4]以福州地铁2号线某区段小净距隧道为工程背景,对循环爆破荷载作用下围岩的累积损伤演化过程进行了研究,发现围岩损伤范围和损伤程度与爆破加载次数成线性增加关系。于丽等[5]将围岩等级、炸药量、净距和交叉角度作为影响因素,对超小净距交叉隧道爆破施工进行了研究分析,依据其结果提出了超小净距交叉隧道爆破的控制标准。刘闽龙等[6]以济南顺河快速路南延工程浅埋暗挖段施工为背景,通过软件LS-DYNA对炮孔周围的损伤范围进行了分析研究,并基于声波测试原理,对施工现场小净距隧道围岩的损伤进行了探测。梁琨等[7]以济南市顺河快速路南延工程为背景,结合数值模拟结果和现场监测数据,针对小净距隧道爆破开挖过程中先行洞在后行洞上台阶爆破作用下的动力响应进行了研究。刘传阳等[8]根据爆破施工现场振动监测数据,研究了隧道分岔段控制爆破振动对相邻隧道的影响,对相邻隧道和后方中隔岩墙在掏槽爆破和预留光爆层爆破条件下的振动影响进行了论证。曹峰等[9]依托六月田分岔隧道为工程背景,采用LS-DYNA有限元软件建立数值模型,分析了循环爆破荷载作用下对小净距隧道中夹岩的影响,并根据损伤区质点振速衰减规律,通过数据拟合,建立一系列爆破变量之间的函数关系。以上学者的研究对小净距隧道实现顺利爆破施工起到了重要作用,然而目前针对先行洞隧道爆破开挖时后行洞隧道围岩的振动速度及应力变化规律研究还较少,有待进一步探索研究。

本文结合浙江义东高速防军小净距隧道工程实际,通过理论分析推导出爆破振动速度与爆心距的关系,运用有限元软件MIDAS GTS NX建立不同净距条件隧道爆破开挖模型,将振速数值模拟结果与理论计算结果进行分析对比,验证理论推导公式的合理性。基于围岩振速及应力两者之间函数关系,提出本隧道爆破控制振速阈值,为本工程及后续类似小净距隧道工程爆破安全施工提供参考。

1 小净距隧道爆破数值模型建立

1.1 工程概况

义东高速防军隧道工程为六车道分离式山岭隧道,左线起于ZK29+047,终于ZK29+557,全长510 m,纵面线形为人字坡,右线起于K29+053,终于K29+562,全长509 m,纵面线形为人字坡。进洞口段位于丘陵斜坡区,地势起伏较大,洞口自然坡度约30°,附近围岩呈松散～碎裂结构,水文地质条件较简单,综合判断进洞口段分布Ⅳ～Ⅴ级围岩。出洞口段位于丘陵斜坡,斜坡自然坡度约20°,表部残破积厚约1.0～2.0 m,其余情况与进洞口类似。隧道洞身段围岩主要为凝灰质砂砾岩夹凝灰质粉砂岩,岩质较软～较坚硬,节理裂隙不发育～较发育,岩石完整性一般～较好,围岩稳定性一般～较好,隧道围岩多为Ⅲ～Ⅳ级。隧道采用钻爆法爆破施工,掏槽采用复式楔形掏槽爆破技术。图1为防军隧道洞口断面设计图。

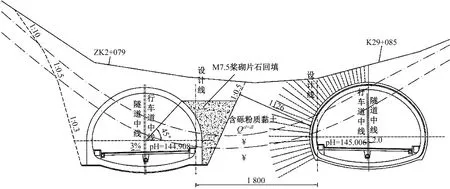
图1 隧道洞口断面设计图Fig.1 Section design of the tunnel entrance

1.2 数值模型

以防军隧道工程为背景,结合工程实际,利用有限元软件MIDAS GTS NX建立三维数值模型,模拟分析时将左洞定义为先行洞,右洞为后行洞,开挖方法采用上下台阶。袁松等[10]认为爆破动力分析时,隧道模型边界大小应取大于等于8倍洞径大小,本文为了合理缩短模型分析时间,保证计算精度,模型X、Y、Z方向大小分别取150 m×150 m×50 m。模型分析时采用单一岩体,通过室内试验得到材料的具体参数取值如表1所示。为分析先行洞爆破开挖对后行洞围岩的影响,建立0.1D、0.5D、D和2D(D为隧道净距14.5 m)隧道净距开挖模型,对围岩的振动速度及应力进行分析研究,数值模型共有20 763个节点,72 707个单元,隧道数值模型如图2所示。

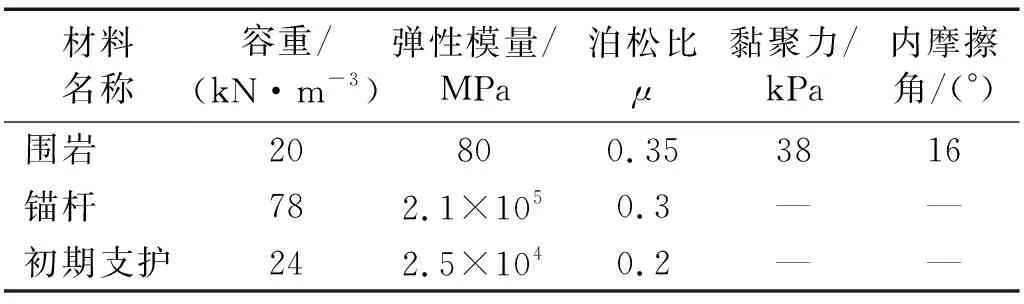
表1 数值模拟材料参数Tab.1 Numerical simulation of material parameters

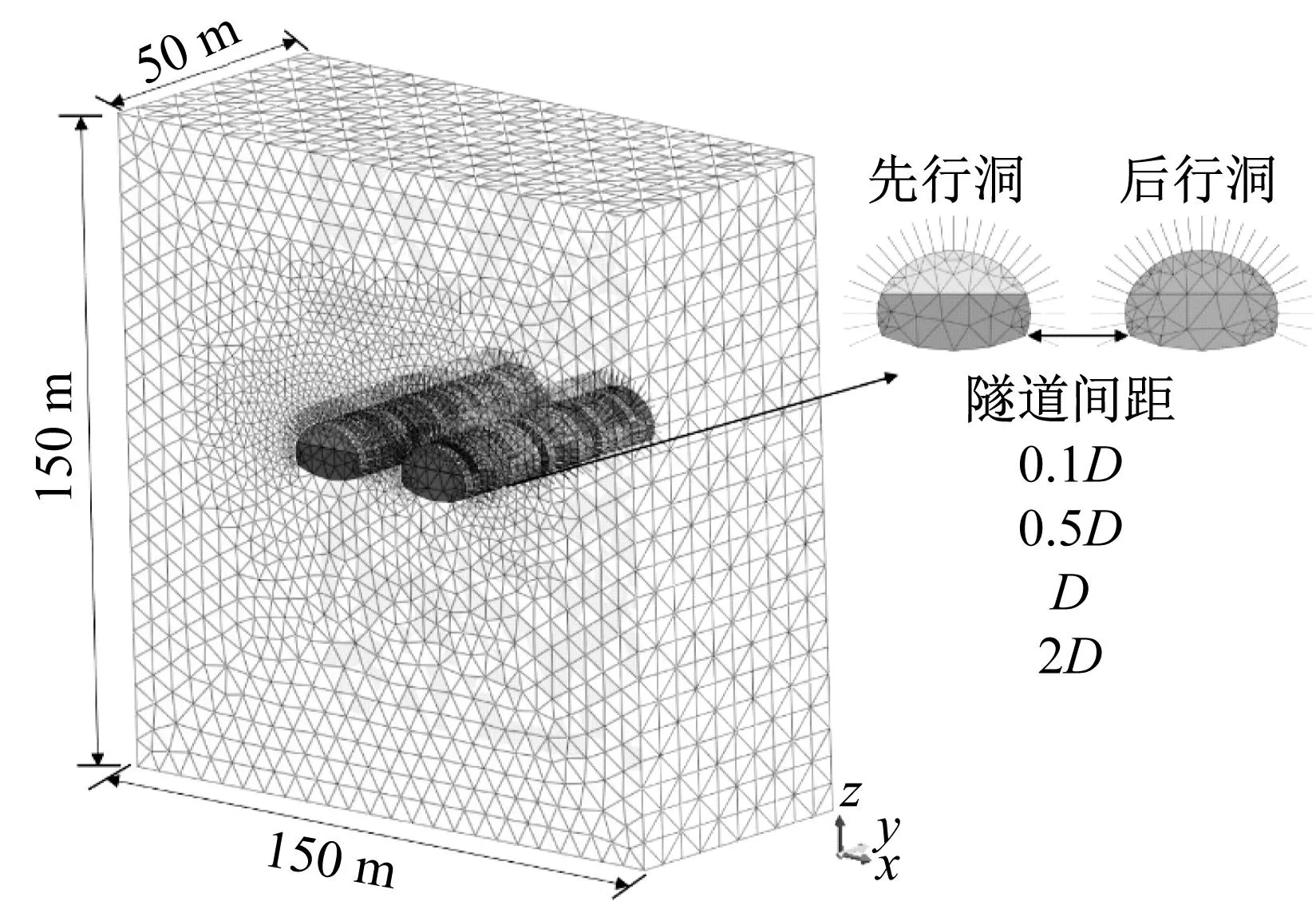
图2 数值计算模型Fig.2 Numerical calculation model

1.3 爆破荷载参数

本文主要研究爆破荷载作用下围岩损伤情况,不考虑其他因素影响,因此将爆破荷载视为均匀地施加在隧道衬砌上,方向垂直作用于洞壁,根据波的传播规律,将爆破荷载形式简化为如图3所示的三角形爆破荷载曲线[11],图中tR荷载升压时间,ts为总作用时间段[12]。模型定义弹性边界条件时曲面弹簧系数由式(1)、(2)求得,所施加的阻尼计算公式如式(3)、(4)所示。

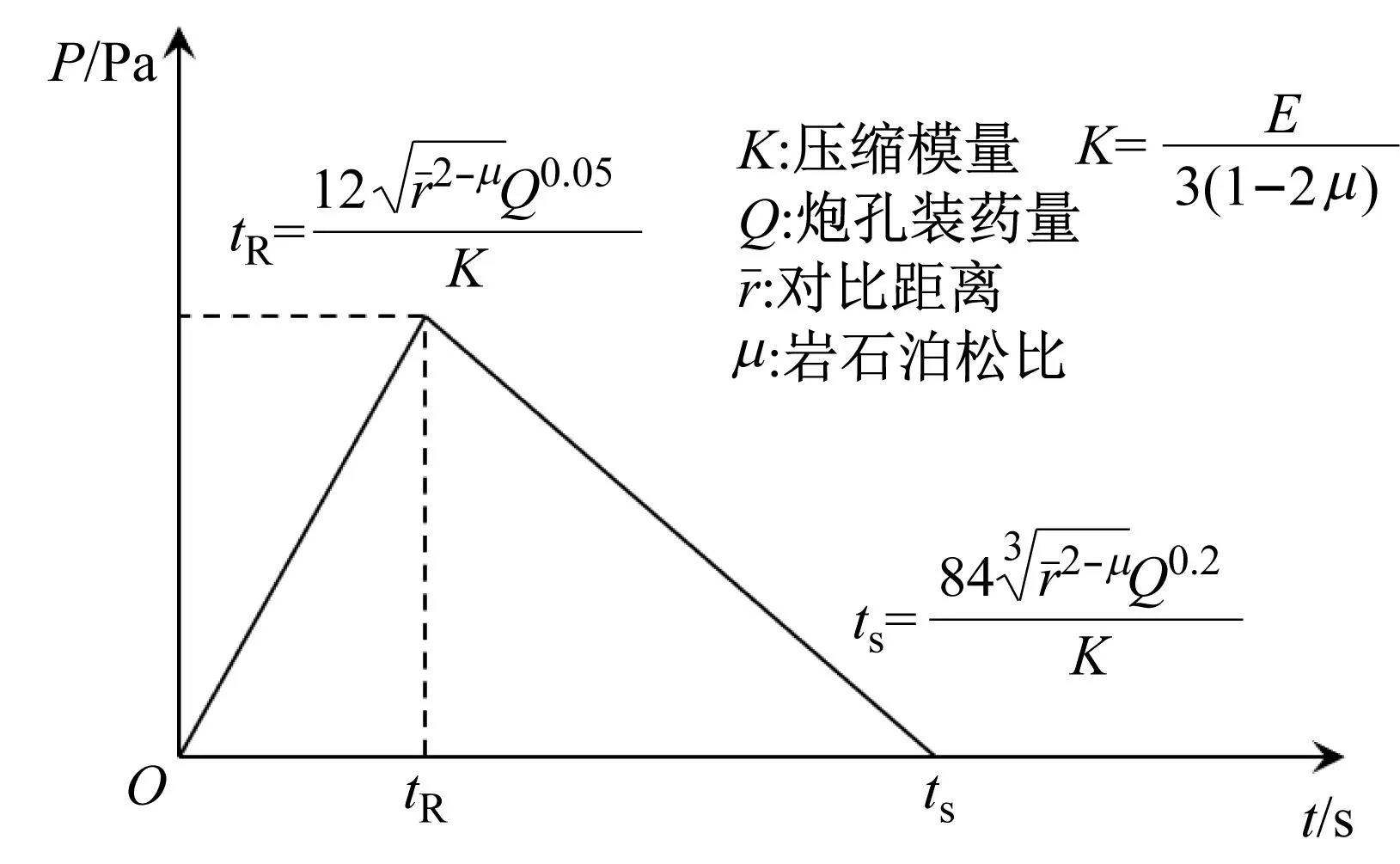
图3 三角形爆破荷载曲线Fig.3 Triangular blast load curve

(1)

(2)

式中:kv0=1/30·α·E0=kh0,Bv=(Av)1/2,Bh=(Ah)1/2,Av和Ah分别是数值模型的竖直方向和水平方向的面积,E0是地基弹性系数,α一般取值1.0[13]。

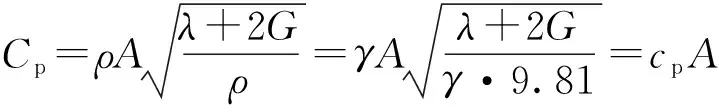
(3)

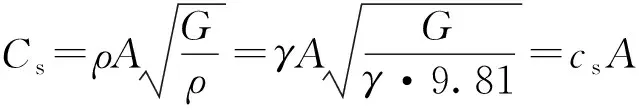
(4)

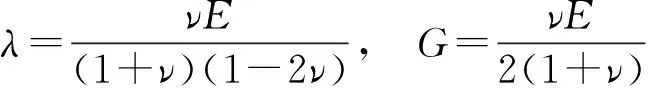
式中:Cp为P波波速(m/s);Cs为S波波速(m/s);A为岩土单元计算面积(m2);E为弹性模量(N/m2);G为剪切模量(N/m2);γ为岩土容重(N/m3);λ为体积模量(N/m2);υ为岩土泊松比;ρ为土层密度(kg/m3)。结合表1与相关文献,计算求得各参数取值分别为A=7 500 m2,G=1.037×107N/m2;λ=6.91×107N/m2,求得土层的阻尼常数为:Cp=359.91 kN·s/m,Cs=137.08 kN·s/m。

防军隧道采用2号岩石乳化炸药,根据其爆破相关参数,模型三角形荷载升压时间取8 ms,卸压时间为92 ms,总时间为100 ms。根据美国National Highway Institute[14]中所运用的式(5)计算爆破荷载峰值大小。式中:db为炮孔直径大小,取db=42 mm;dc为药筒直径,取dc=32 m;Pdet为每kg炸药的爆炸压力(Pa);PB为作用于孔壁的爆破压力(Pa);sge为炸药比重(kg/m3);v为炸药爆速(m/s);工程实际台阶法施工时预计每段最大用药量44.4 kg,炸药比重取1.15 kg/m3,炸药爆速取3 200 m/s,计算防军隧道爆破时每1 kg炸药产生的压力PB=1.13×107Pa,开挖每段压力大小为5.02×108Pa。

(5)

2 小净距隧道后行洞围岩振速理论预测分析

考虑到爆破释放的冲击波在传播过程中具有一定衰减特性,当超过一定范围后,冲击波将转化成具有周期的地震波。由于后行洞隧道围岩距离先行洞爆破中心较远,因此后行洞围岩在先行洞隧道爆破过程中主要受地震波的影响。受各种因素影响的地震波在传播过程中能量不断减少,消耗的能量与传播距离成正比,具体表达如式(6)所示[15]

E=E0e-2βr

(6)

式中:E为地震波传播距离r时的能量;E0为初始能量;r为地震波的传播距离;β为介质对能量的吸收系数。

地震波初始能量E0与炸药总能量Ee之比为能量转换系数η[16-17],其中η=10-3(k·10-2)3/a。

E0=ηEe=10-3(k·10-2)3/aEe

(7)

将式(7)代入式(6)得

E=e-2βr10-3(k·10-2)3/aEe

(8)

隧道爆破时产生的能量与围岩振速平方成正比

(9)

结合式(7)～(9)可得振动速度与爆破距离之间的关系见式(10)

(10)

等式两边开平方得到式(11)

vr=10-3/2·v0(k·10-2)3/(2a)e-βr

(11)

式中:vr为爆心距r时的围岩振速大小;v0为爆破开始时的初始速度,将其视为爆源处岩石的振动速度;k为地形、地质系数;α为衰减指数。β可通过其与振幅之间的关系式(12)拟合计算[18]。

(12)

式中,A为爆破地震波振幅。

防军隧道项目结合场地条件及工程实际,对系数k,α分别取k=150,α=1.5。地震波吸收系数β通过施工现场爆破振速和爆心距监测数据整合处理,进行拟合分析。施工现场对隧道出洞口段邻近水库坝体进行了爆破振动监测,测得质点XYZ三个方向的振速大小。目前通过单方向的振速大小(peak particle velocity, PPV)难以准确描述爆破特征,故引入振速三个方向的矢量和(peak velocity summation, PVS),其表达形式见式(13),文献[19]证明PVS可以提供更加准确的振动速度估算。

(13)

通过CAD设计图纸测得爆破监测点与爆源之间距离,振速大小与爆心距之间关系如图4所示。将振速矢量和PVS与爆心距两者进行拟合分析,结果如图5所示,拟合公式为y=726.584 5e-0.067 52x,R2=0.966 51。结合式(12)及拟合结果,防军隧道岩层介质吸收系数β取0.034。

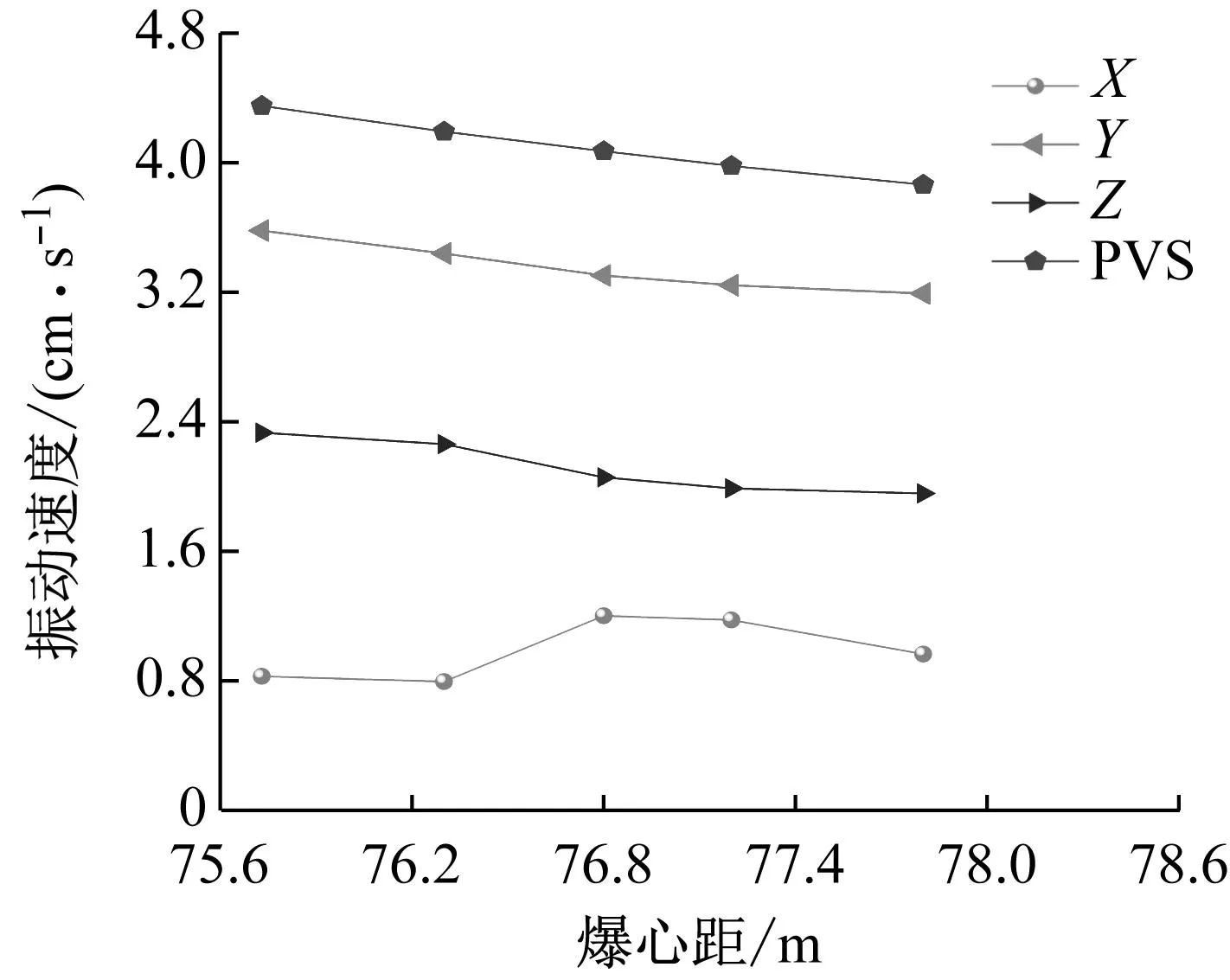
图4 质点各方向振动速度随爆心距变化曲线Fig.4 The curve of particle vibration velocity in each direction with detonation distance

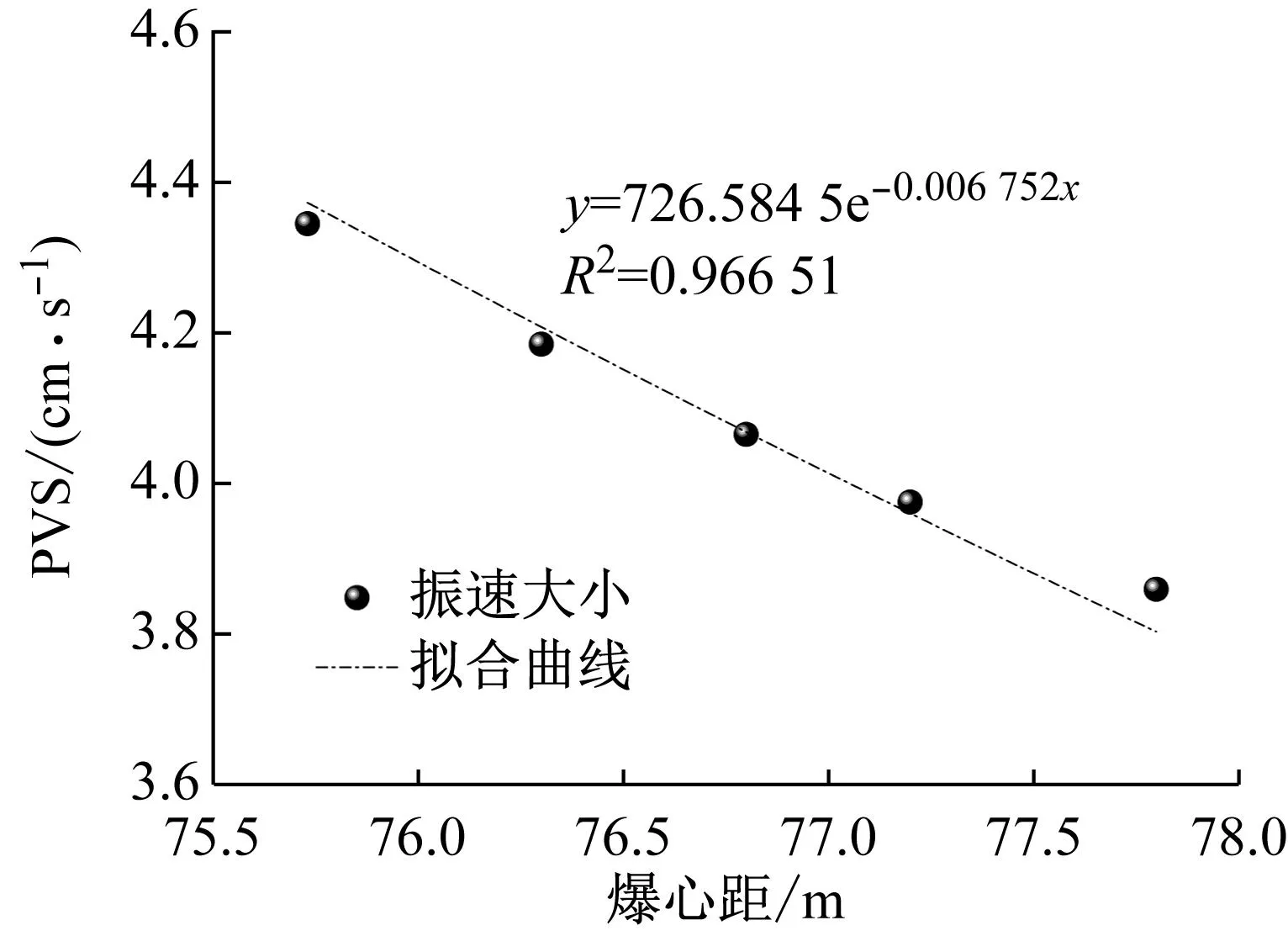
图5 振速矢量和PVS与爆心距拟合分析Fig.5 The fitting analysis of the vibration velocity vector PVS and detonation distance

综合上述分析,将爆破系数k、a、β代入式(11),可得防军隧道工程爆破施工时,地震波在岩石介质传播过程中振速与爆心距之间的关系式为

vr=10-3/2·v0(150·10-2)e-0.034r=

0.047v0e-0.034r

(14)

通过式(14)可对后行洞隧道围岩振速进行预测分析。防军隧道爆破施工时,由于受到施工条件的限制,因此无法通过现场监测获得后行洞隧道预贯通段围岩的应力重分布和破坏形态。为此,根据所建立的数值模型,设置不同工况,对先行洞隧道爆破过程中后行洞隧道围岩振速大小、应力分布情况进行深入分析。

3 数值模拟计算与分析

模型模拟时,采用与工程相同的上下台阶法,选取不同净距条件下相同隧道断面进行分析,左右洞掌子面处于同一平面内。沿隧道开挖轮廓线共布置8个监测点,具体布局如图6所示。其中1～5号监测点位于迎爆侧面,6～8号监测点位于背爆侧面。

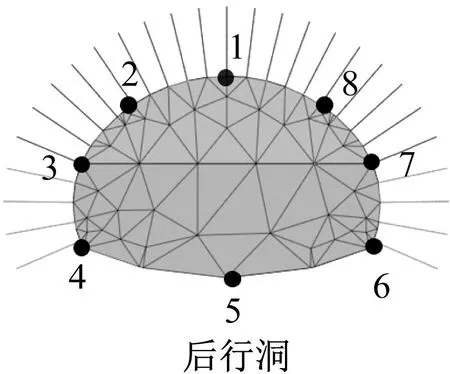
图6 隧道围岩监测点布置图Fig.6 Layout of the tunnel surrounding rock monitoring points

3.1 振动速度分析

图7为不同净距条件下后行洞围岩监测点振速峰值雷达图。

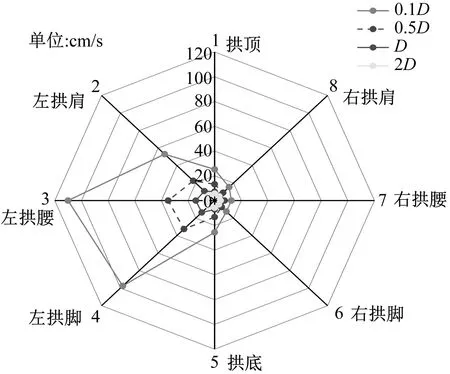
图7 不同净距条件监测点振速雷达图Fig.7 Radar chart of vibration velocity at monitoring points with different clear distance conditions

由图7可知,围岩最大振速始终出现在3号监测点,即拱腰处,拱腰与拱脚两者大小较为接近,围岩振速大小从拱腰→拱脚→拱肩→拱顶(底)逐渐减小,施工时应对隧道拱腰及拱脚处加强监测。随着隧道净距逐渐增大,同一监测点的振速峰值随之减小。

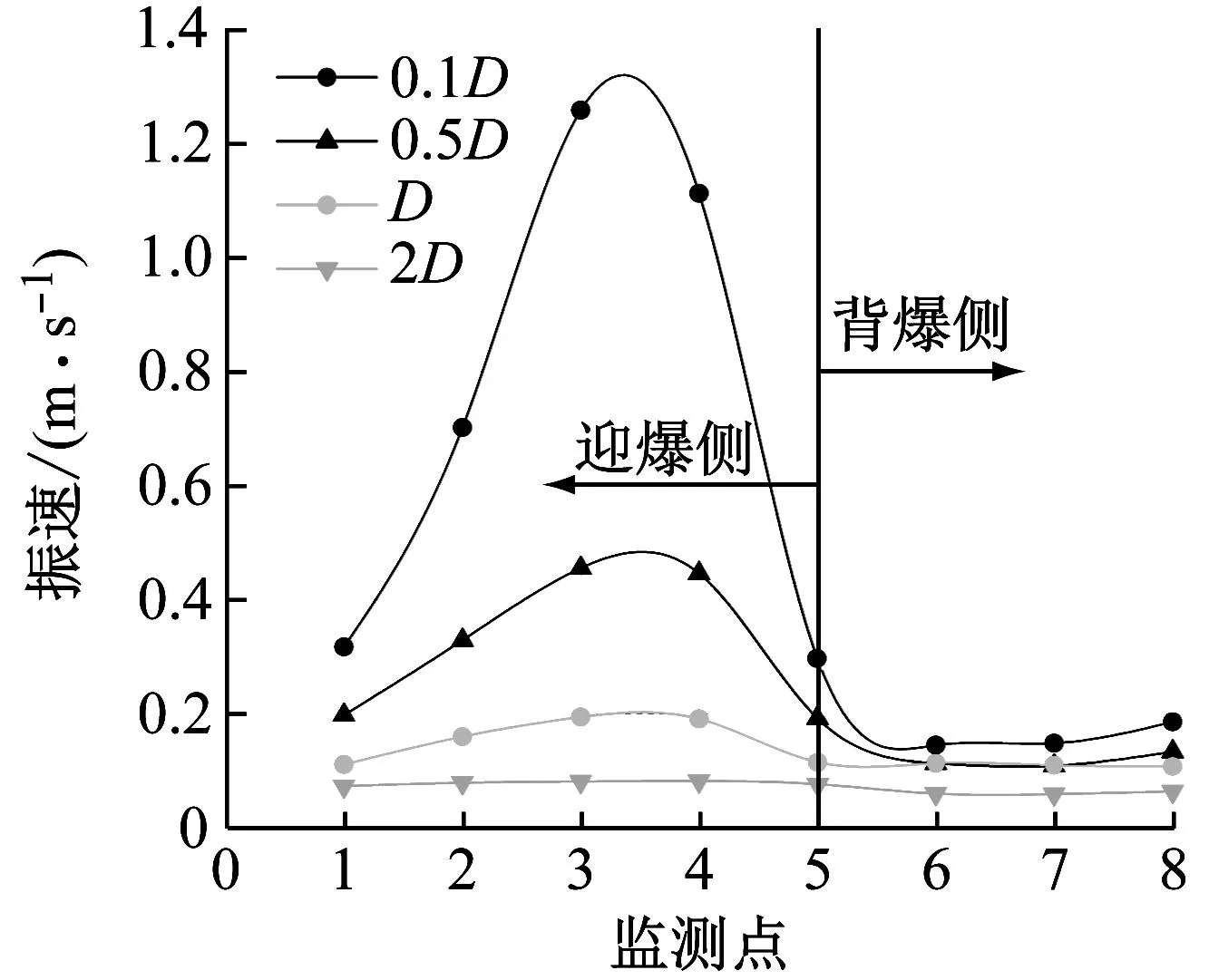
图8(a)、(b)分别为后行洞上台阶与下台阶开挖后围岩监测点振速对比图。

(a) 上台阶开挖

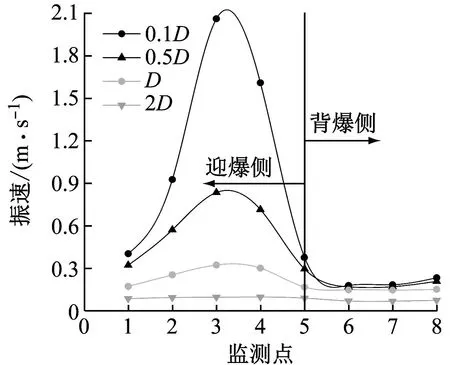
(b) 下台阶开挖图8 不同净距条件监测点振速峰值对比图Fig.8 Comparison of the peak vibration velocity of monitoring points with different clear distance conditions

根据GB 6722—2014 《爆破安全规程》[20]规定交通隧道的质点安全振动速度控制标准为10～20 cm/s,考虑到防军隧道出口邻近水库坝体,为此本文隧道振速安全控制阈值取10 cm/s。由图7可知,在相同净距条件下,迎爆侧监测点振速远大于背爆侧,后者约为前者的0.5倍～0.8倍,且背爆侧监测点振速总体变化趋势较小。由于左右隧道之间围岩的存在消耗了部分爆破产生的能量,故随着隧道净距的增大,同一监测点的振速越小,总体变化曲线逐渐朝直线发展。当隧道净距为0.1D时,后行洞隧道围岩的八个测点最小振速达到了12.47 cm/s,超过了控制标准,此时先行洞隧道爆破振动易对后行洞隧道围岩稳定性造成影响,文献[21]将围岩质点振速大小作为隧道爆破后围岩损伤判据,在最不利工况0.1D净距条件下,下台阶开挖后围岩最大振速峰值为206.4 cm/s,文献[22]中的Bauer和Calder判据认为当振速峰值大于63.5 cm/s小于254 cm/s时,围岩会产生严重的拉伸裂缝及一些径向裂缝,因此后行洞预贯通段应提前采取相应措施,防治爆破对隧道稳定性造成不利影响。当隧道净距大于2D时监测点振速均满足规范要求,结合项目实际情况,将隧道净距2D作为安全净距的分界线。在相同净距条件下,开挖下台阶时隧道同一位置的振动速度大于上台阶,隧道净距越小,两者的振速差值越大。在安全净距2D条件下,上台阶开挖最大振速峰值为8.23 cm/s,下台阶为9.87 cm/s,后者约是前者的1.2倍。

3.2 应力分析

图9～12为不同净距条件下先行洞开挖围岩最大主应力σ1(kN·m2)变化云图。

(a) 上台阶

(b) 下台阶图9 净距0.1D条件下围岩应力分布Fig.9 Stress distribution of surrounding rock with a net distance of 0.1D

(a) 上台阶

(b) 下台阶图10 净距0.5D条件下围岩应力分布Fig.10 Stress distribution of surrounding rock with a net distance of 0.5D

(a) 上台阶

(b) 下台阶图11 净距D条件下围岩应力分布Fig.11 Stress distribution of surrounding rock with a net distance of D

(b) 下台阶图12 净距2D条件下围岩应力分布Fig.12 Stress distribution of surrounding rock with a net distance of 2D

通过图9～12发现,先行洞隧道爆破时,应力变化主要集中在先行洞隧道围岩周围,应力影响范围随着隧道净距的增加而扩大,左右隧道间中隔岩壁的应力大小随着净距的增加而逐渐减小,净距为2D时,提取左右洞间某点,发现其应力大小达到了约0.71 MPa,且后行洞隧道围岩及中隔岩壁的应力值均小于其抗拉强度,表明此时先行洞爆破对其稳定性造成的影响几乎忽略不计,隧道整体处于安全稳定状态。上台阶开挖后,先行洞隧道围岩的最大应力主要分布在下台阶顶部附近,下台阶开挖后,围岩最大应力主要分布在掌子面拱底与拱腰附近,应力分布范围较大,下台阶开挖后的影响范围远大于上台阶,净距为0.1D条件下,上台阶开挖后围岩最大主应力为4.26 MPa,下台阶开挖后为6.13 MPa,最大主应力大于岩石抗拉强度时,会导致隧道局部围岩开裂,严重时造成围岩坍塌。随着净距的增大,围岩应力总体呈减小趋势,先行洞隧道爆破开挖对后行洞隧道围岩的影响逐渐减小,最终趋于稳定状态。

3.3 振速计算理论验证

为了验证振速理论预测公式(14)的合理性,取隧道净距D时振速数值模拟结果与理论计算值进行对比分析。隧道净距为D时左右洞掌子面平行距离为14.5 m,纵向以10 m为一间隔,即爆心距r的取值分别为17.6 m、24.7 m、33.3 m、42.5 m、52 m,将数值模拟中爆源处围岩的振动速度作为v0,其值为1.6 m/s。理论计算值与模拟值对比结果如图13所示。由图13可知,爆破施工过程中振速理论计算结果与模拟结果相对误差较小,最大相对误差为5.7%,通过数值模拟方法的验证,说明本文基于理论推导的振动速度预测公式具有一定合理性。

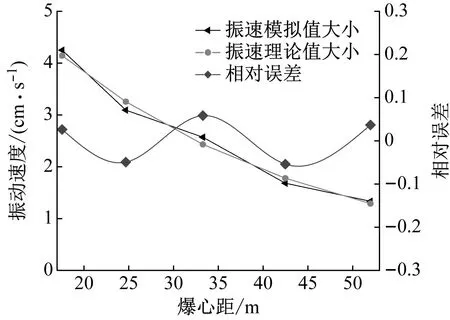
图13 净距D条件下围岩理论计算值与模拟值对比Fig.13 Comparison of theoretical and simulated values of surrounding rock with a clear distance D

4 隧道振动安全标准及工程实例

4.1 振速安全标准

目前,工程实践上对隧道振动速度控制阈值的设定主要依赖于规范要求及施工经验,对振速如何合理取值方面还鲜有研究。先行洞爆破开挖时,后行洞围岩在不同净距条件下的应力峰值和振速峰值变化情况如图14所示。由图14可知,围岩左拱腰及拱脚的振动速度最大,为围岩振动响应的危险处,整体来看,围岩最大应力及振速皆随着净距的增大而减小,从统计学角度出发确立围岩应力峰值与振速峰值两者间函数关系。

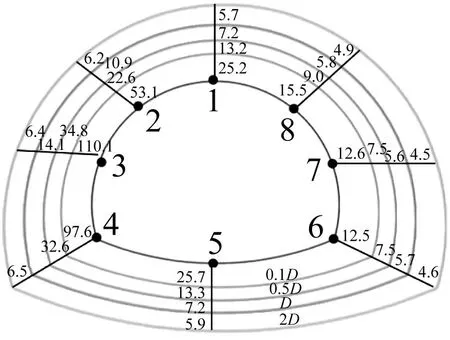
(a) 振速峰值(cm/s)

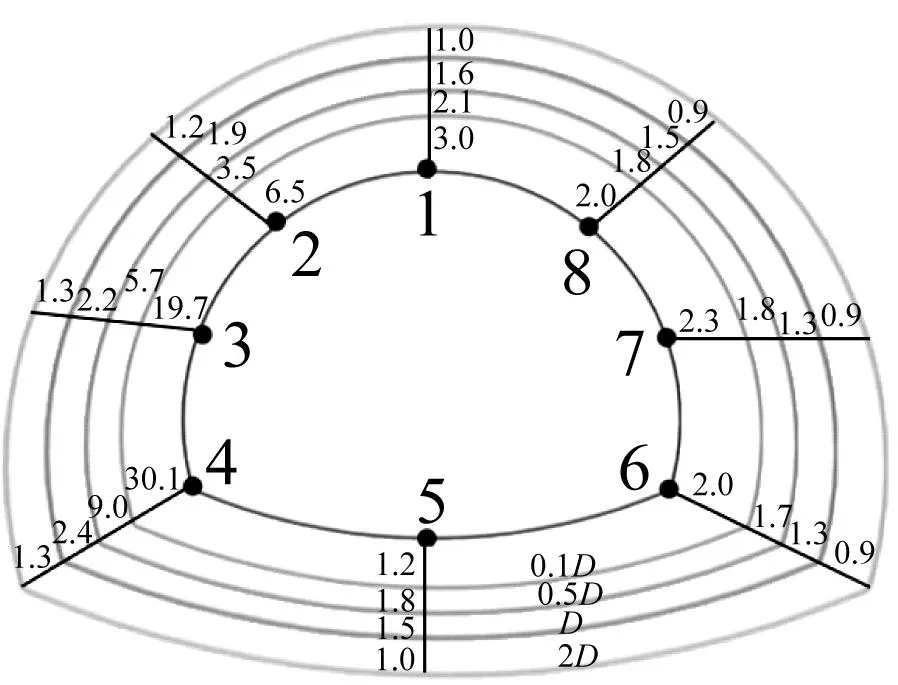
(b) 应力峰值(MPa)图14 围岩在不同净距条件下应力及振速峰值Fig.14 Peak stress and vibration velocity of surrounding rock under different clear distance conditions

图15为隧道振速峰值与应力峰值的统计关系,两者之间的关系表达式为

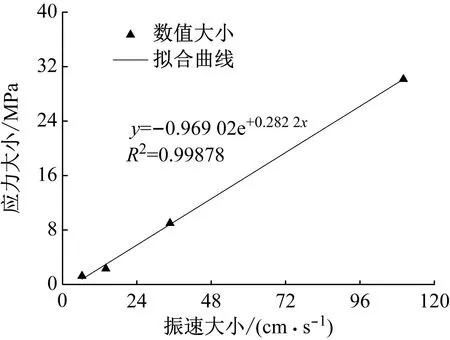
图15 围岩振速大小与应力大小的统计关系Fig.15 Peak velocity and stress fitting analysis of the surrounding rock

σ=-0.969 02+0.282 2v

(15)

式中:σ为应力大小,MPa;v为振速大小,cm/s。在式(15)中,R2=0.998 78,结果表明后行洞隧道应力峰值与振速峰值具有较好的线性关系。当围岩应力小于其抗拉强度时,表明围岩处于安全稳定状态,依据岩石的抗拉强度可计算得到爆破作用下围岩振动速度控制阈值。综合考虑防军隧道地质情况,隧道岩石抗拉强度大小取3.5 MPa,将其代入式(15),计算得到:当围岩振动速度峰值为1.9 cm/s时,所受应力达到其抗拉强度。

4.2 工程案例

根据爆破应力波的传播理论,既有隧道在爆破施工时,为了保证邻近隧道的安全,须对爆破强度进行控制,进而避免对相邻隧道造成不利影响。防军隧道进口段为小净距部分,左右洞掌子面之间距离较小,为了降低爆破扰动影响,防军隧道施工现场根据爆破断面的位置,对爆破震动的影响范围进行初步估计,在其影响范围内的隧道断面上布设L20-N爆破测振仪对围岩振速进行监测。

防军隧道施工现场振动监测如图16所示。进口段围岩振速监测数据如表2所示。通过表2可以得到,隧道桩号K29+075、095、115三者PVS理论大小与现场监测相对误差分别为7%,2.66%,2.58%,结果表明理论研究结果能够较好的应用于实际工程,通过理论计算从而避免爆破施工对围岩稳定性造成不利影响。

图16 施工现场爆破振动监测Fig.16 Construction site blasting vibration monitoring

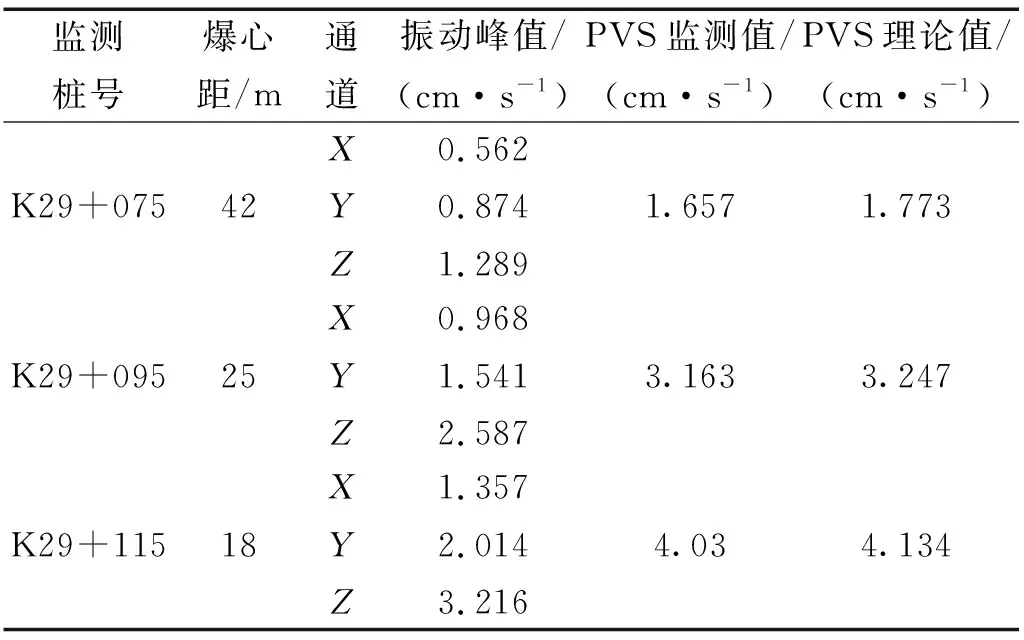
表2 隧道进口段振速监测数据Tab.2 Vibration velocity monitoring data of tunnel entrance section

5 结 论

针对先行洞隧道爆破施工对后行洞围岩稳定性影响问题,本文基于能量衰减理论,结合数值模拟手段,对后行洞隧道围岩振速及应力变化规律进行了研究。主要结论如下:

(1) 围岩振速理论计算值与模拟值最大相对误差为5.7%,与现场监测数据最大相对误差为7%,表明该理论能较好地应用于相应隧道,对隧道爆破安全施工研究具有一定的工程应用价值。

(2) 振速峰值与隧道爆破中心距呈负相关,爆心距越大,对围岩扰动越小。根据振速分析结果,将净距2D定义为最小安全净距,左右洞隧道间距小于2D时,应加强对后行洞隧道围岩的监测。

(3) 隧道后行洞围岩迎爆侧监测点振动速度大于背爆侧,其结果从拱腰→拱脚→拱肩→拱顶(底)逐渐减小,相同净距条件下,同一监测点下台阶爆破时振速峰值大于上台阶。随着净距增大,先行洞爆破对后行洞围岩的扰动逐渐减弱,最终忽略不计。

(4) 不同净距爆破开挖作用下,后行洞隧道围岩的应力峰值与振速峰值具有线性关系,两者随着净距的增大而减小,隧道拱腰及拱脚为易发生破坏的危险点。根据岩石的抗拉强度计算得到防军隧道爆破振动速度安全阈值为1.9 cm/s,为类似工程提供了确定控制振速阈值的方法。