二维声学黑洞应用于压电振动能量收集
陈 兵, 张杨坤, 任 江, 尹忠俊
(北京科技大学 机械工程学院,北京 100083)
声学黑洞(acoustic black holes,ABH)将物理学中的黑洞概念引入到声波和振动领域中,并将其作为一种全新的概念提出。声学黑洞效应通过结构阻抗的变化﹐引起结构中波的相速度和群速度发生变化,在结构局部区域实现波的聚集[1-2]。
近年来,随着物联网技术的不断发展,无线传感器网络、便携式可穿戴设备等低功耗电子产品得到了广泛的应用,电池有限的使用寿命使得低功率电子设备难以维护。机械振动能是最常见的能源,存在于生产车间、车辆、船舶运输、隧道、桥梁施工、人体运动等领域。例如直升机的驾驶舱,直升机在飞行过程中,整个动力传动系统包括主旋翼、尾桨、发动机、传动齿轮及其附属组件,这些旋转部件都会间接或直接向驾驶舱传递振动。由于直升机飞行工况的变化,这种声源的典型频率呈现宽带特性,覆盖200~3 000 Hz范围。其采集的能量可用于供应机内低功耗的电子设备。在压电振动能量回收领域,可以利用ABH结构将高度集中的振动能量转化为电能。
对于简单的ABH结构,如经典的一维和二维结构,主要采用几何声学方法[3-4]和半解析方法[5-7]进行研究,而比较复杂的结构通常采用有限元方法[8-9]进行研究。许多研究人员对各种类型的ABH结构进行了试验研究,进一步证明了ABH在实际应用中的潜力。ABH现象在过去十年中引起了研究者的极大兴趣,使其在弯曲波控制等工程技术中得到了许多应用[10]。例如,用于工业系统中涡轮叶片[11-12]的减振,通过嵌入周期ABH单元[13-15]实现低频减振,为控制面板[16-18]的瞬态响应设置周期ABH单元。本研究可为周期结构和超材料的发展提供参考。近年来,关于压电振动能量采集[19-21]的研究越来越多。在前期探索中,Zhao等[22-23]对简单的一维梁结构和二维薄板结构进行了试验研究,初步证明了ABH结构应用于能量收集的可行性。Deng等[24]提出了一种基于能量的半解析方法来研究一维梁结构的ABH能量收集器。Li等[25]在压电悬臂梁方程中引入压电晶体和外部电路,通过模态机电耦合因子优化每个压电片的最佳位置和尺寸。Zhang等[26]在机电耦合模型中引入了非线性因素,在研究结果中发现了大量的非线性现象。
上述关于压电振动能量采集的研究大多集中在一维梁结构上,对于工程上常见的薄板结构,特别是在保证结构强度的前提下实现压电振动能量采集的研究较少。许多学者发现附加结构对ABH效应有显著影响,但很少有人研究如何在应用中定量描述并且避免这种影响。本文在二维薄板结构的基础上,提出并研究了一种用于压电振动能量收集的环形ABH结构。该结构可以在较宽的频率范围内实现较高的能量采集效率,并在非共振频率下保持较高的功率输出。研究了压电能量收集装置对ABH效应的影响,得到了能获得最佳能量收集效果的压电片(piezoelectric patch, PZT)尺寸范围。仿真和试验表明,该结构性能良好,并为实际应用提供了一定的参考。
1 环形二维声学黑洞能量收集器设计
1.1 弯曲波在声学黑洞中的传播规律
经典一维梁式ABH结构通常由两部分组成:等厚度部分和ABH部分。一维梁式ABH的几何厚度方程为
(1)
式中:h1(x)为梁的厚度;h1为梁均匀部分的厚度;k为ABH区域高度的控制系数;α为幂指数;L为总长度;LABH为ABH部分长度。
根据欧拉-伯努利理论,在一维介质中,弯曲波动方程可表示为
(2)
为了简化方程,局部刚度定义为
D(x)=E(x)h1(x)2/12(1-ν2)。
式中:ρL(x),E(x)和ν分别为介质的密度、弹性模量和泊松比;ω为弹性波的圆频率;w(x)为楔形梁的弯曲位移。
将ABH梁的几何厚度方程代入波动方程,可得到弯曲波周期的表达式
(3)
式中:cgr为弯曲波的群速度;ρ为梁的材料密度;x0,x1为梁在长度L方向上的两点。
当α≥2时,理论上弯曲波传播到尖端时,其周期T趋于无穷,弯曲波的相速度趋于0。弯曲波的能量将集中在ABH结构的尖端,不能被反射。
二维薄板结构中弯曲波的传播方程为
ω2ρh(x,y)w=0
(4)
式中:D(x,y)为二维薄板结构的局部刚度;h为薄板厚度。
弯曲波的波长和薄板厚度的平方根成正比
(5)
当薄板的厚度形状按照指数形式变化时,可形成二维薄板型声学黑洞,振动能量将集中于声学黑洞结构的中心,从而有利于进行能量收集。
1.2 模型建立
本文所设计环形二维声学黑洞能量收集器模型及截面,如图1所示。
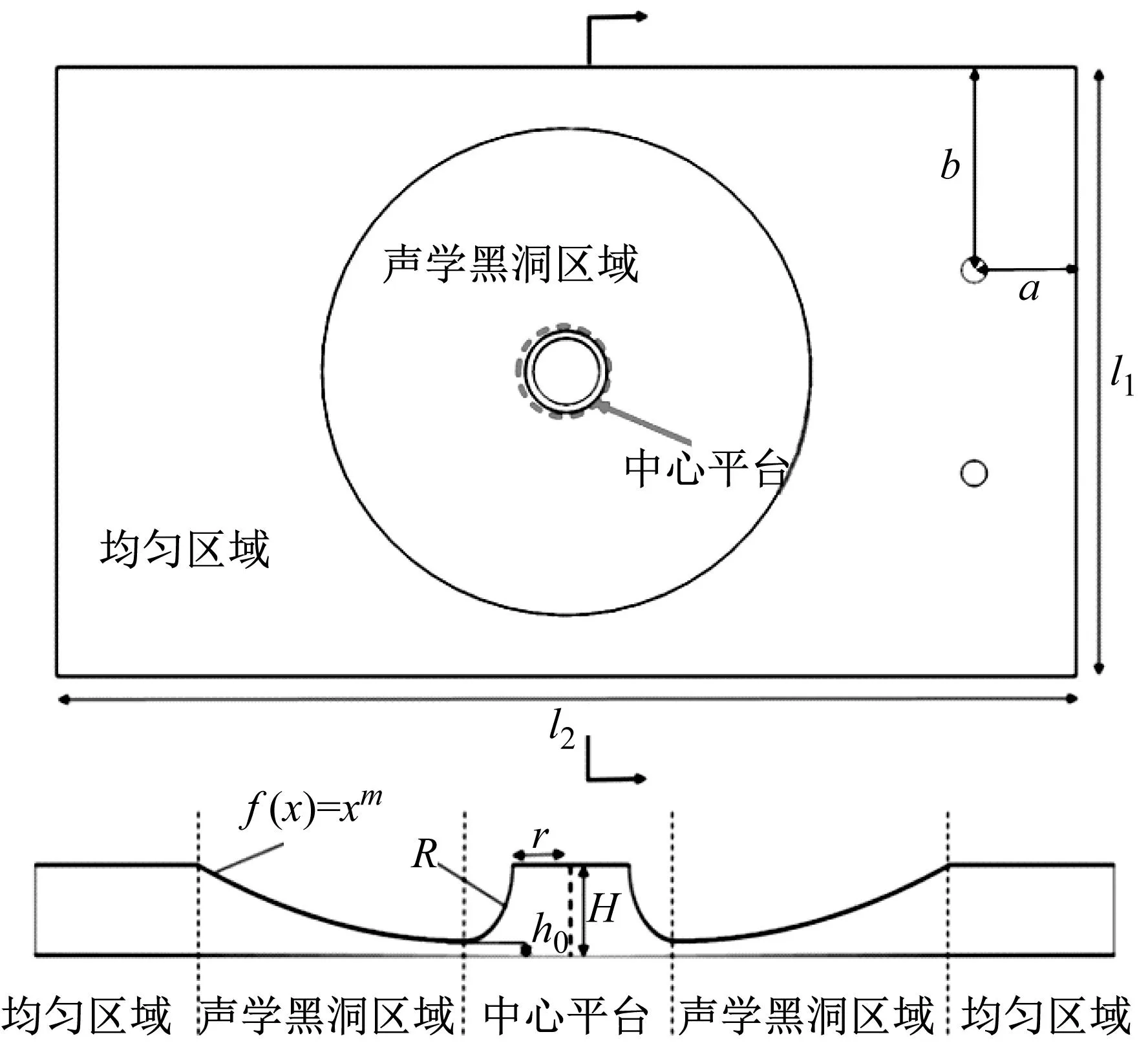
图1 环形二维声学黑洞能量收集器模型及其截面Fig.1 Annular 2-D acoustic black hole energy collector model and its cross section
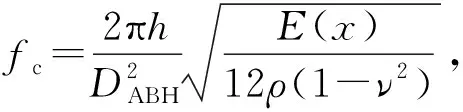
外接电路原理图,如图2所示。压电片布置位置,如图3所示。将四个压电片放置于二维ABH板表面与ABH轮廓相对应的平整一侧,并紧贴中央平台边缘放置。
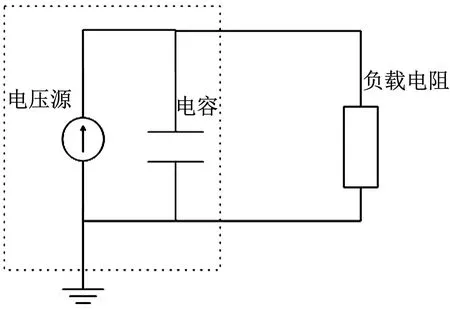
图2 外接电路原理图Fig.2 Schematic diagram of external circuits
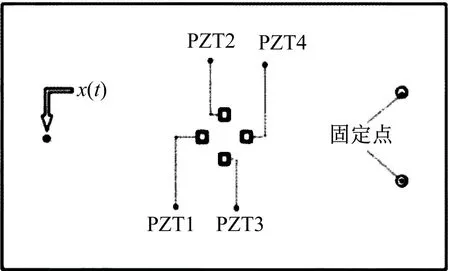
图3 压电片布置位置Fig.3 Placement of piezoelectric patches
根据相关学者的设计经验及试验条件来设计环形ABH板的几何尺寸,使得实际加工的薄板便于进行试验。表1和表2分别为环形ABH板和压电片的几何参数。表3和表4分别为两者的材料参数。
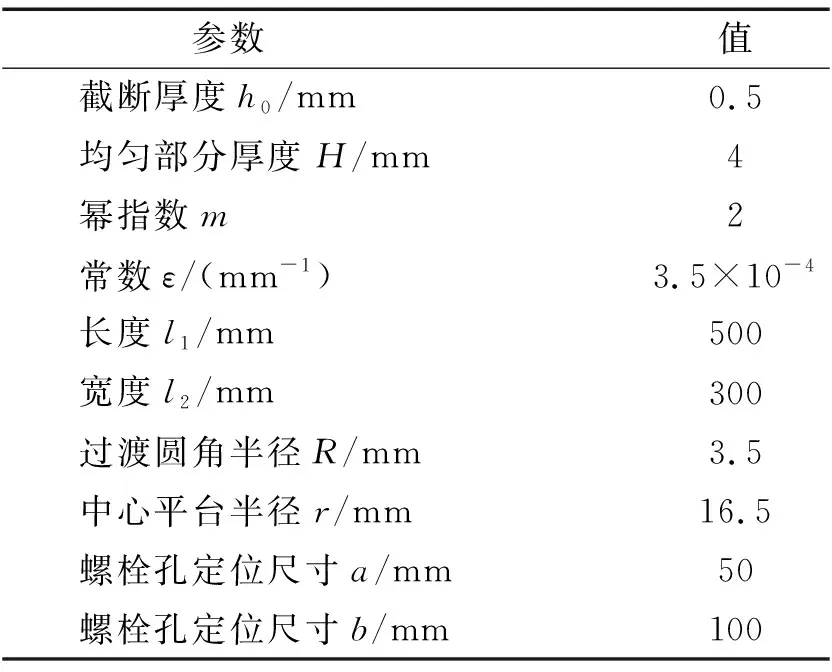
表1 环形ABH板的几何尺寸Tab.1 Geometric dimensions of annular ABH plates

表2 压电片的几何尺寸Tab.2 Geometric dimensions of piezoelectric patches

表3 环形ABH板的材料参数Tab.3 Material parameters of annular ABH plates
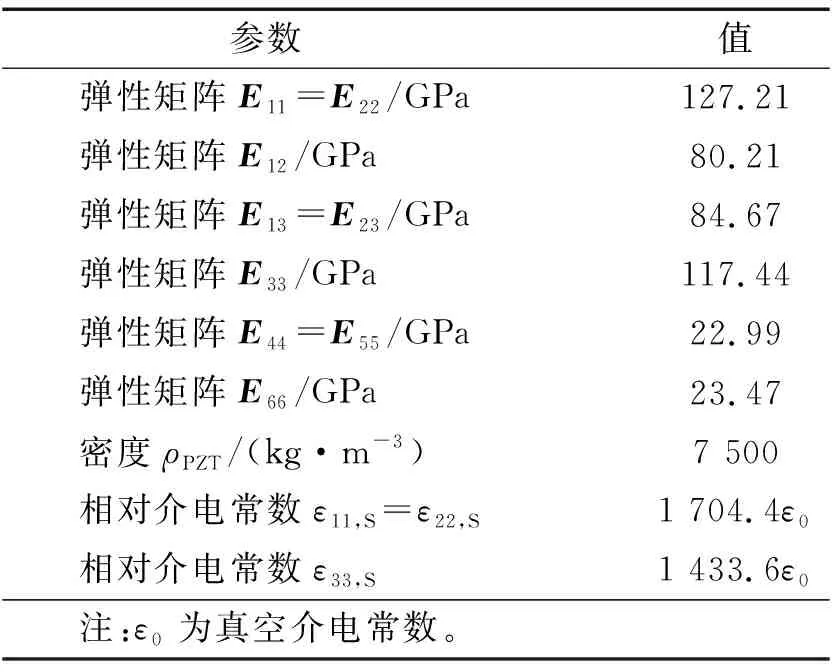
表4 压电片的材料参数Tab.4 Material parameters of piezoelectric patches
2 仿真分析
在实际环境中,激励源的频率组成比较复杂。为了覆盖尽可能多的频域以接近实际环境,本文从两个角度对所设计的能量收集装置进行了仿真研究。从瞬态激励的角度,研究了单激励信号条件下环形二维ABH板的弯曲波传输和能量收集特性。从稳态激励的角度,通过在0~2 000 Hz范围内进行扫频试验,研究了所设计的能量收集装置对多种单频信号的响应特性。
用COMSOL/Multiphysics软件完成仿真。在使用有限元方法研究弯曲波时,网格密度通常需满足每个波长内至少包含10个单元,考虑到波在ABH板中的弯曲以及中心区域的局部厚度变化,为保证精度,在实际划分中每个波长内至少包含40个单元。
2.1 瞬态响应分析
在瞬态响应分析中,只能存在一个激励信号。因此,激励信号应具有较宽的频域。本文采用的激励信号为高斯调制激励,如图4所示。其频域可以完全包括0~2 000 Hz的频率范围,其表达式为
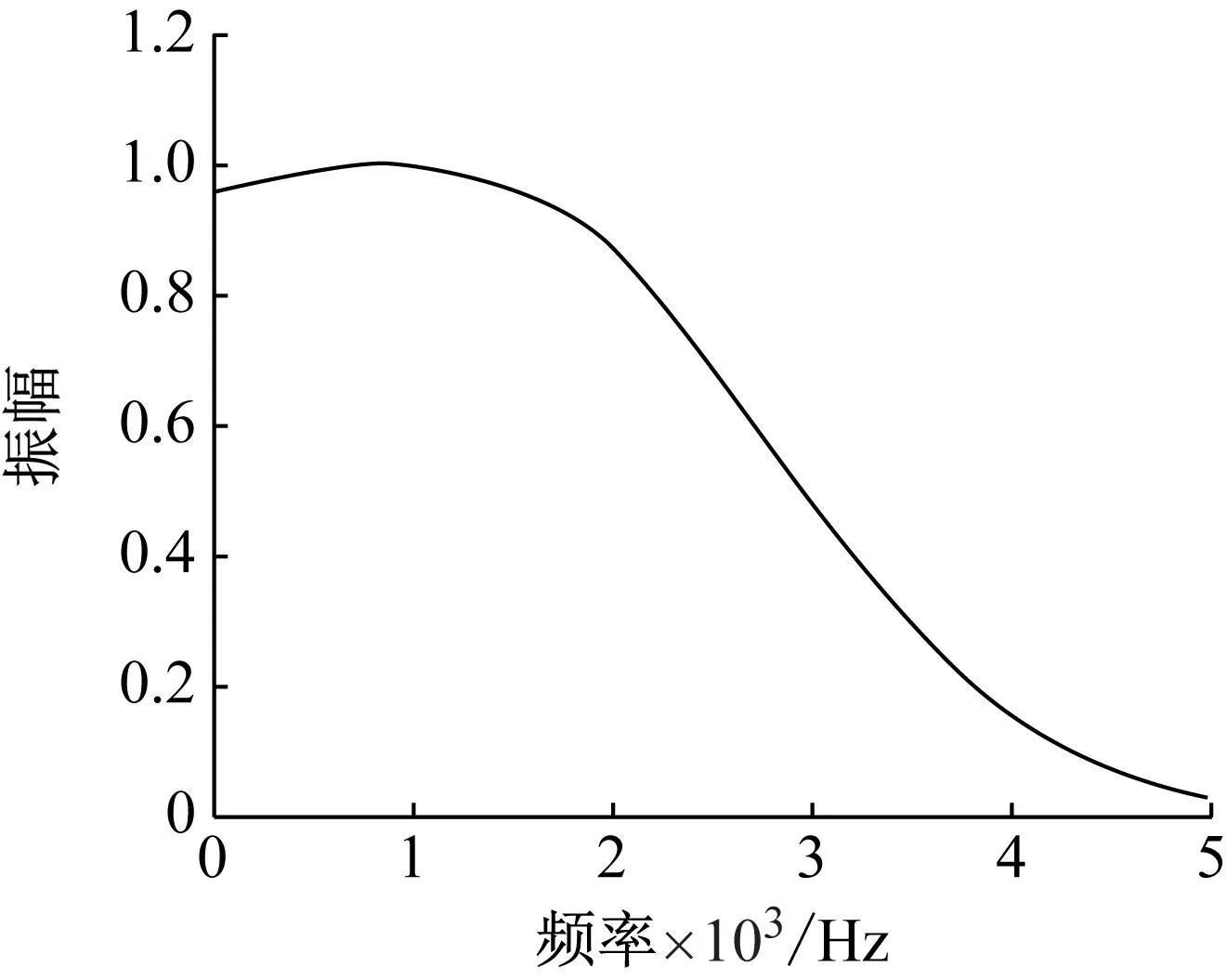
图4 激励信号归一化频谱Fig.4 Normalized spectrum of excitation signals
4.48×10-4))
(6)
位移激励在0~1 ms内施加,1~10 ms为去除位移激励后的响应。时间步长设置为0.001 ms,以保证足够的计算精度。通过对环形ABH板的应变场观测,确定了其振动能量集中效应。如图5所示,获得了两个结构在同一仿真时间(4.3 ms)的第一主应变云图。由图5可知,大应变区域集中在环形ABH板的中心,说明该结构有效地聚集了振动能量。在均匀板作为对照组上,应变分布极为分散,大量振动能量分布在薄板平面上,难以集中利用。随着去激发时间的增加,两者之间的差距逐渐增大,甚至在4.3 ms处达到一个数量级。

(a) 环形ABH板

(b) 均匀板图5 应变张量分布Fig.5 Strain tensor distribution
对所设计的环形ABH能量收集器和均匀板在机电耦合下的能量收集效果进行了测试。将四个位置的压电片的输出功率求和,以评价整体的功率输出能力。研究结果如图6所示。去除位移激励后,环形ABH能量收集器的输出功率明显高于均匀板,且随时间快速衰减。这说明集中在环形ABH板中心的大量振动能量在很短的时间内转化为电能。
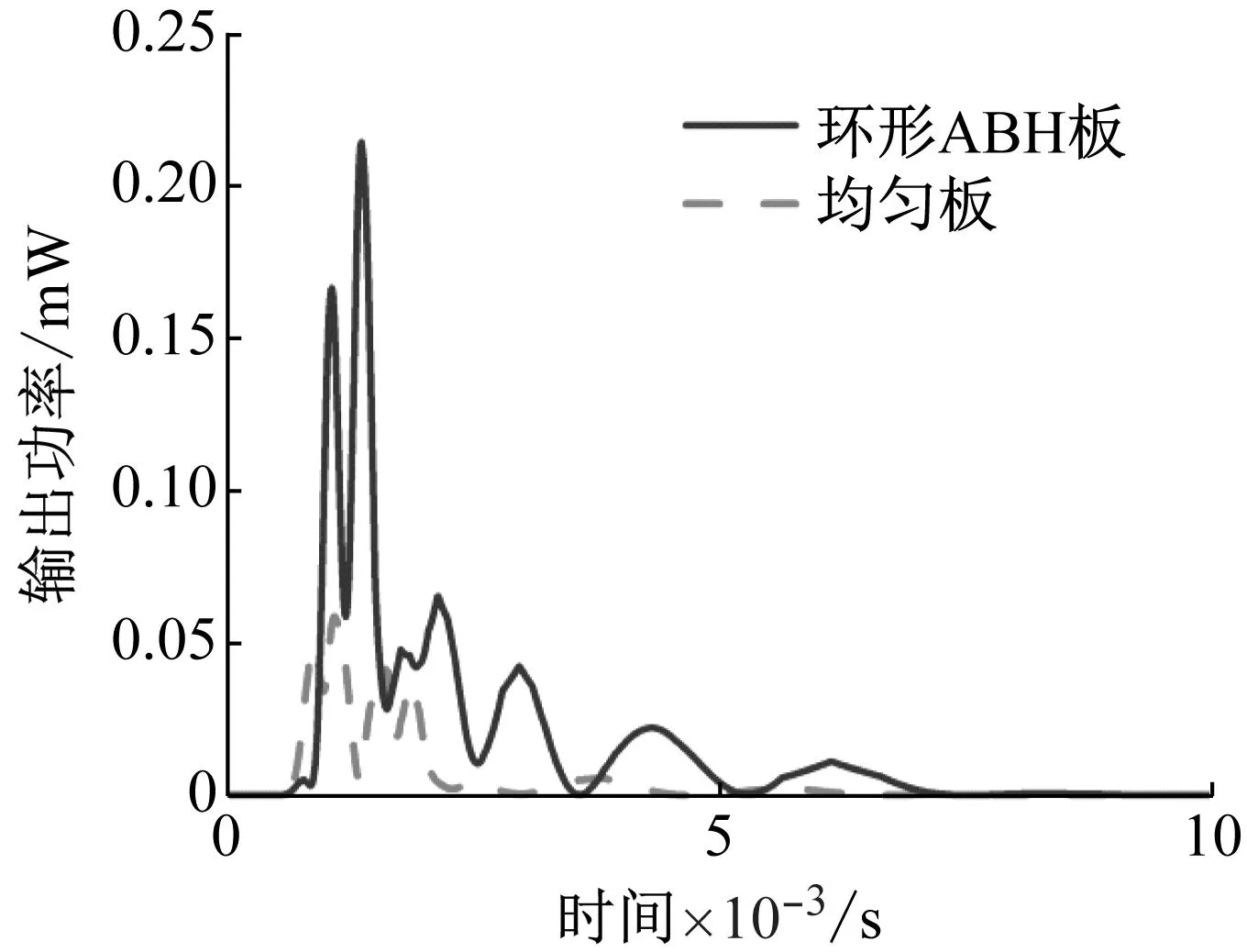
图6 环形ABH板和均匀板的瞬态输出功率Fig.6 Transient output power of annular ABH plate and uniform plate
提取压电片在各位置的输出电压数据,结果如图7所示。每个压电片的对应位置在1.2节中已经提到,由于2号和3号压电片完全对称的布置,曲线2和曲线3几乎完全重叠。根据与激励源距离的不同,四个压电片的输出电压依次出现峰值。首先是离激发源最近的1号,其次是两侧对称分布的2号和3号,最后是离激发源最远的4号。在第一个峰值,1号和4号显著高于2号和3号,1号略高于4号。在第二个峰值,1号和4号之间有时间差,但峰值非常接近。
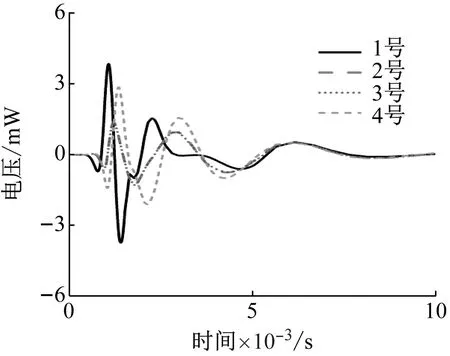
图7 不同位置压电片输出电压Fig.7 Output voltage of piezoelectric patches at different positions
2.2 稳态响应分析
真实环境中的振动激励信号总是连续的。对所设计的能量收集器的频域稳态激励响应进行了研究。与2.1节所使用的高斯调制信号不同,稳态响应研究将激励信号作为施加在相同位置的大小恒定的激励力,此处选取激励力为1 N。在0~2 000 Hz范围内,对两个能量收集器进行频率扫描,频率间隔为10 Hz。同理,将各压电片的输出功率相加得到整体输出功率,结果如图8所示。
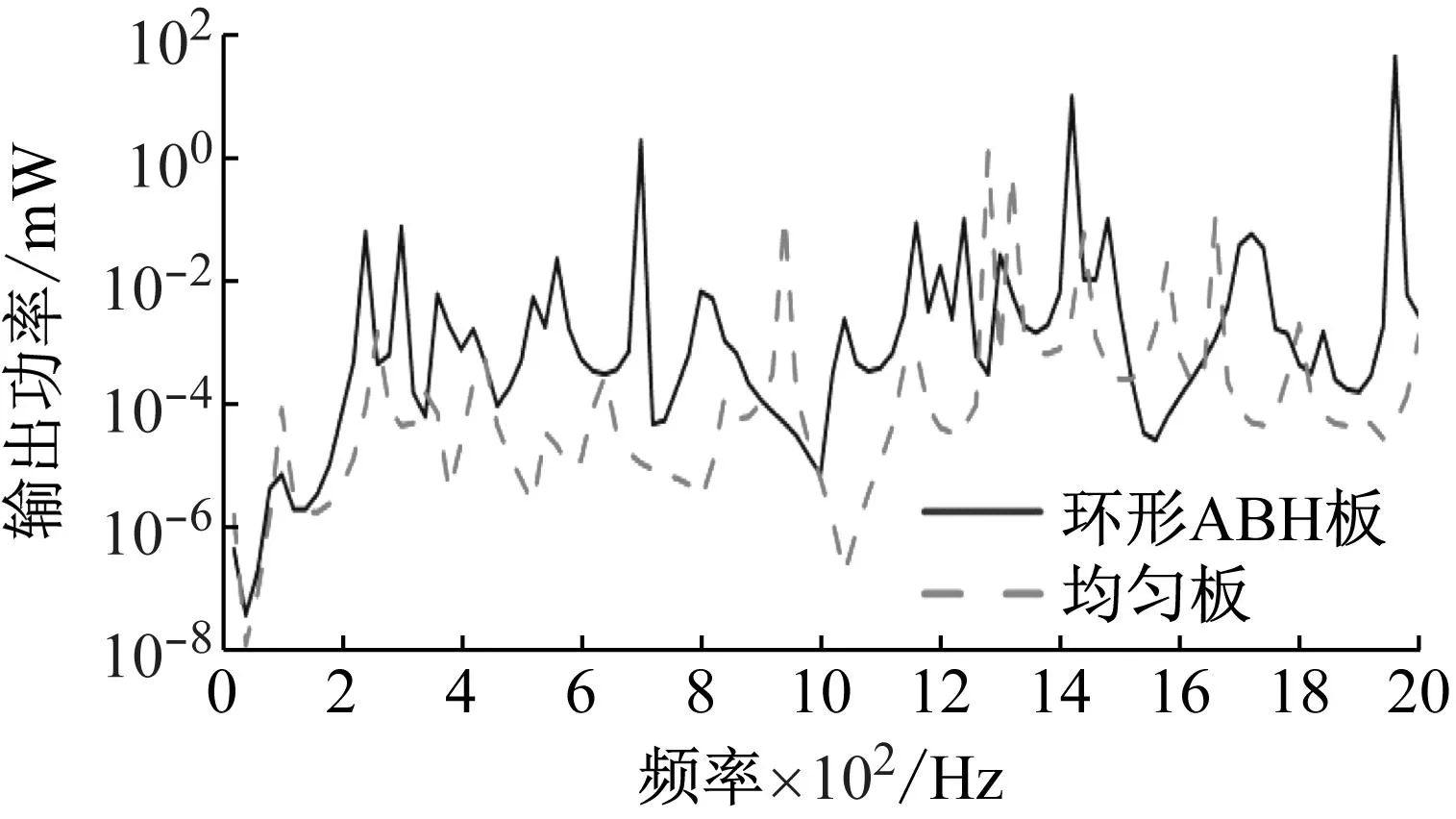
图8 扫频试验:环形ABH板和均匀板Fig.8 Frequency sweep test: annular ABH plate and uniform plate
通过对比两种输出功率曲线,可以看出环形ABH板在大部分频域范围内具有明显的优势。两者在大多数共振频率下均有较高的输出功率,但是环形ABH板在非共振频率时仍具有较高的输出功率。
在ABH末端,即压电片靠近中心平台的位置,标记出参考点,四个参考点的位移均方根可以表示能量聚集程度。结果如图9所示。由于结构和位置的对称性,标记点2和3具有相同的位移均方根,对应的两条曲线重合较好。标记点1和4的位移均方根在整体趋势上是一致的,在整个频域上都高于标记点2和3的位移均方根。标记点4距离激励源最远,所以其振动强度略低于标记点1。
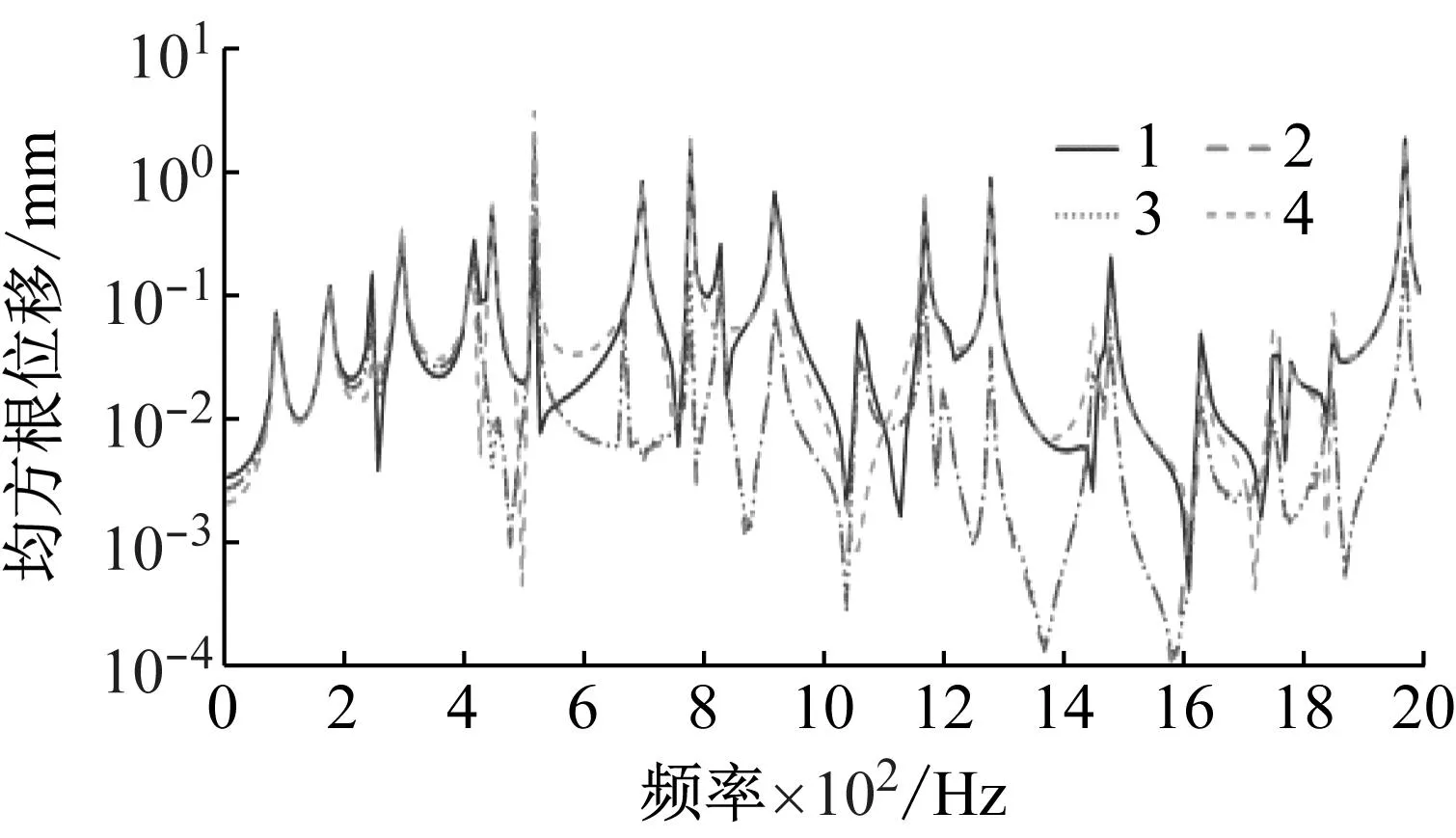
图9 四个点位移的均方根值Fig.9 Root mean square values of displacement at four points
由于标准二维ABH板难以加工,目前的研究多采用带有截断平台的二维ABH结构。这里以黄薇等[27]研究的模型为参考。中心截断圆直径40.0 mm,厚度0.5 mm。输出功率对比如图10所示。可以看出,在所研究的频域内,除个别频率外,环形ABH板的输出功率均高于经典二维ABH板。较小的截面积使环形ABH板具有优异的结构强度和更高的结构可靠性,同时实现能量收集。
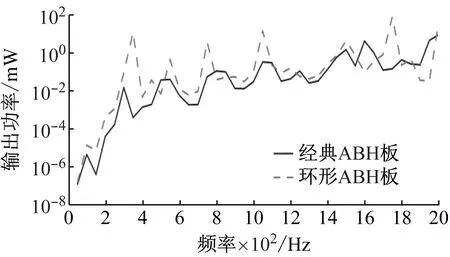
图10 输出功率:环形ABH板与经典ABH板Fig.10 Output power: annular ABH plate and classic ABH plate
3 试验与分析
通过试验方法验证和评价了环形ABH结构振动能量收集系统的能量收集特性。加工了环形ABH板和均匀板。通过对压电能量收集系统测量点的电信号输出进行评估,验证了环形ABH板提高能量回收效率的效果。
试验系统原理图,如图11所示。试验系统主要由压电振动能量收集板、电磁振动台、数字示波器及相关电路组成。根据仿真模型对压电能量收集板几何尺寸进行1∶1处理,如图12所示。其材料参数、几何参数与仿真模型一致,可参考表1、表2。为了尽量减少导线数量,降低电路布置难度,四个压电片共用一个输出端。利用铝合金材料的导电特性,将公共输出端设置在压电振动能量收集板的边缘,最大限度地减少附加导线对ABH结构振动能量收集效果的影响。
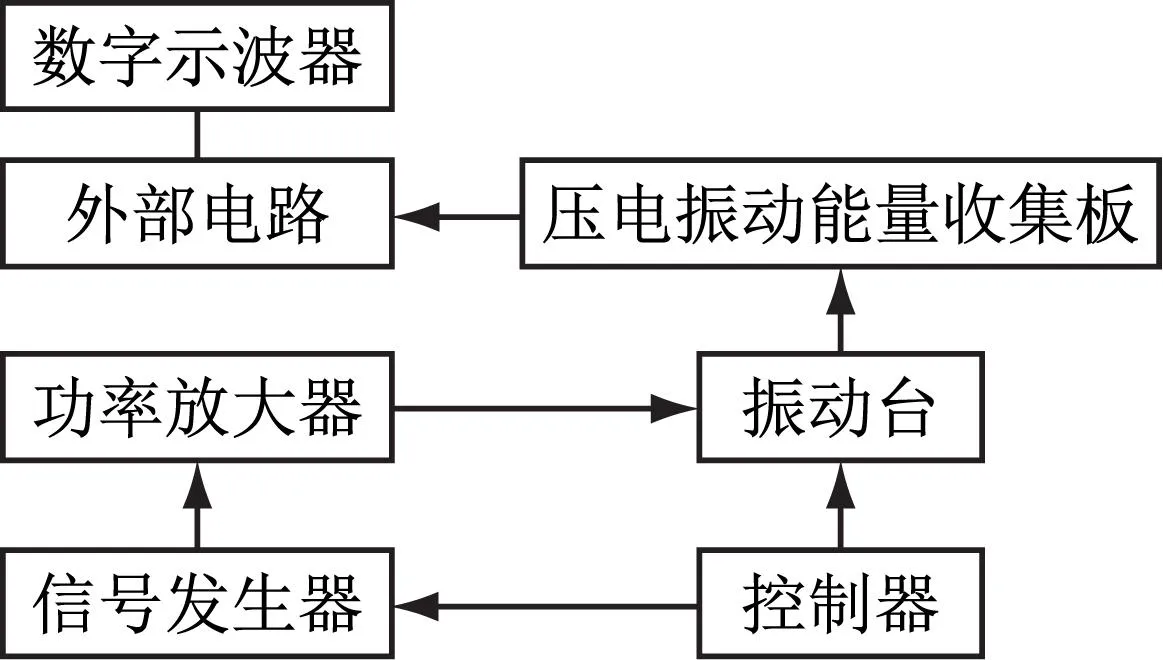
图11 试验系统示意图Fig.11 Test system schematic

图12 环形ABH板Fig.12 Annular ABH plate
用酒精清洗两块板的表面,然后在规划区域放置10.00 mm×10.00 mm×0.31 mm的压电片。在压电片边缘涂强力胶,使压电片固定在铝合金板上,并与铝合金板保持良好接触,以保证两者之间的导电性。试验装置如图13所示,在振动台平面上布置ICP型加速度传感器和电涡流位移传感器,跟踪振动台的输出频率、加速度和位移。
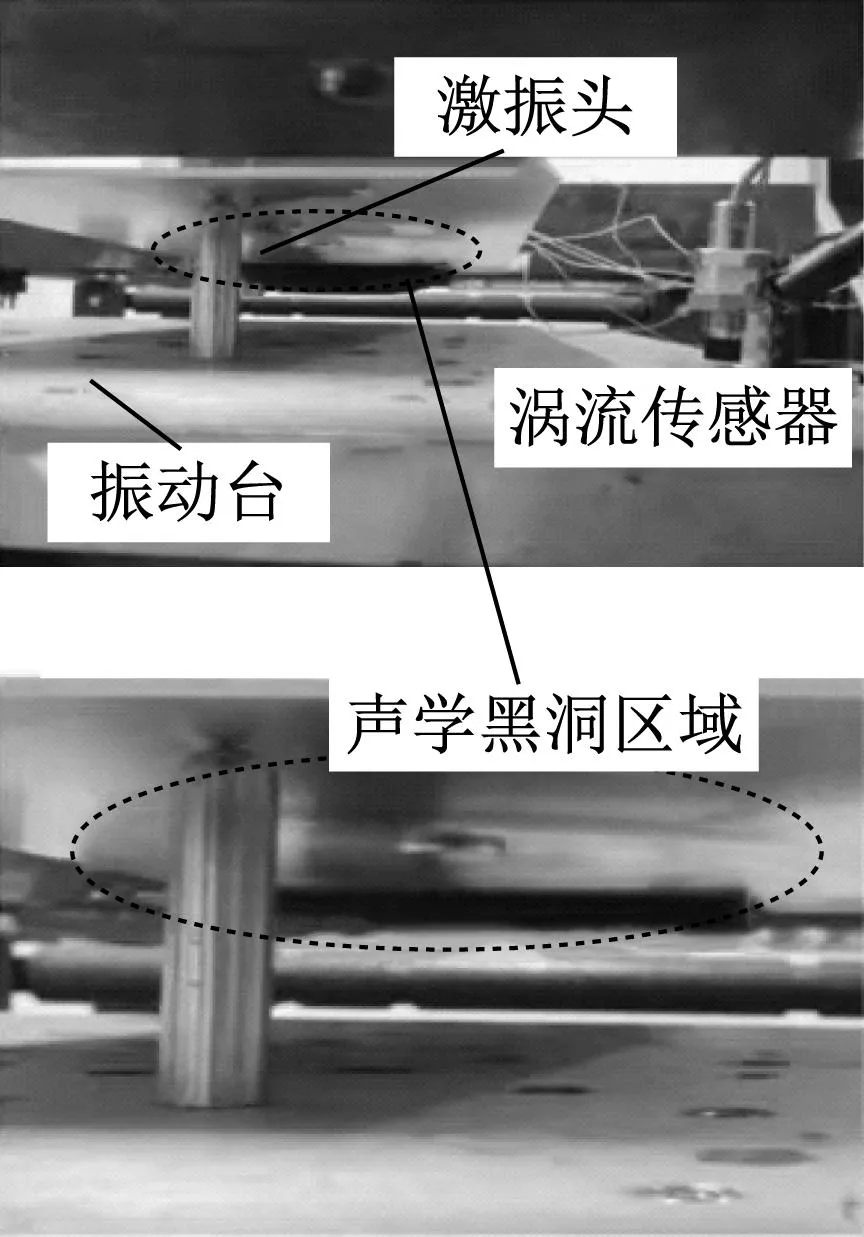
(a) 侧视图

(b) 俯视图

(c) 数据采集与输出图13 试验装置Fig.13 Test device
在100~2 000 Hz范围内,每隔100 Hz进行定频激励,逐个记录每个位置的输出电能。振动台控制软件设置的理论输出位移值分布如图14(a)所示。图14(b)为数字示波器在520 Hz激励下显示的输出电压波形。图14(c)为520 Hz激励下涡流位移传感器输出的位移信号,理论峰值为20 μm。涡流传感器采集的信号表明,振动台位移的峰间值基本保持在20 μm。
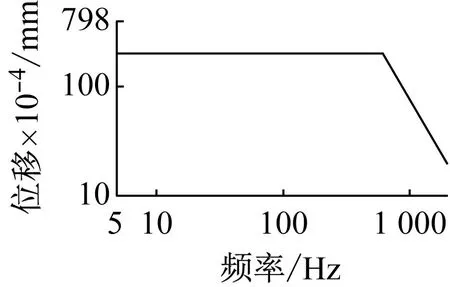
(a) 理论位移
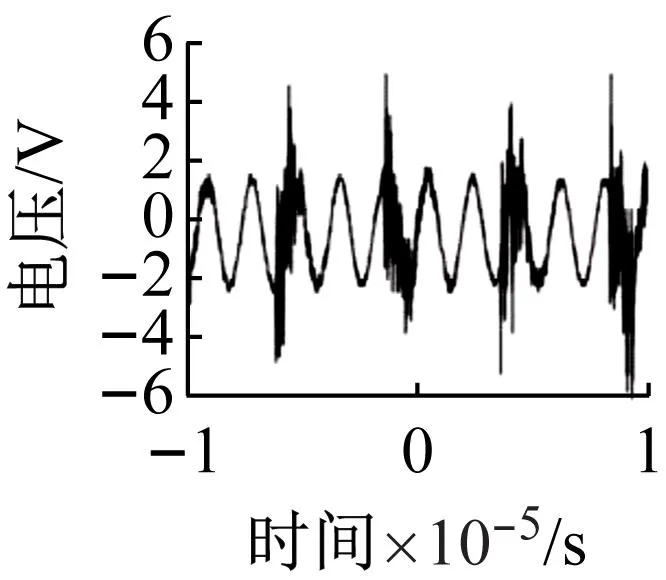
(b) 示波器输出信号
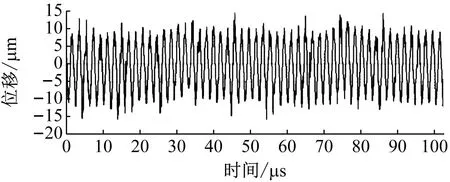
(c) 电涡流传感器输出波形图14 试验数据Fig.14 Test data
记录环形ABH板四个位置的压电片输出功率,结果如图15所示。由图15可知,PZT2和PZT3对应的曲线基本重合,证明试验装置的布置对称性良好。除个别频率外,PZT1和PZT4整体输出功率较高,PZT4略低于PZT1。这可能是PZT4靠近固定端造成的。
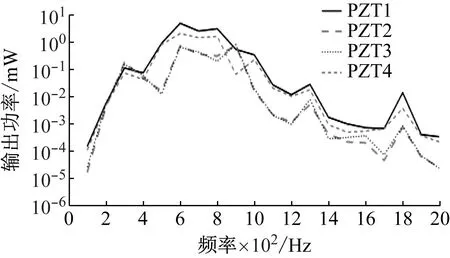
图15 四个压电片的输出功率Fig.15 The output power of four piezoelectric patches
环形ABH板与均匀板的输出功率对比,如图16所示。1号、2号和4号压电片的输出功率明显高于均匀板。环形ABH板在宽频率范围内实现了较好的振动能量回收。
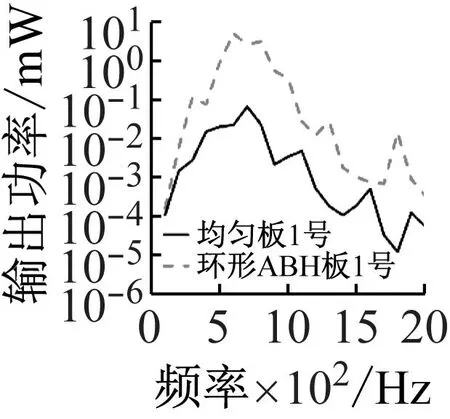
(a) PZT1
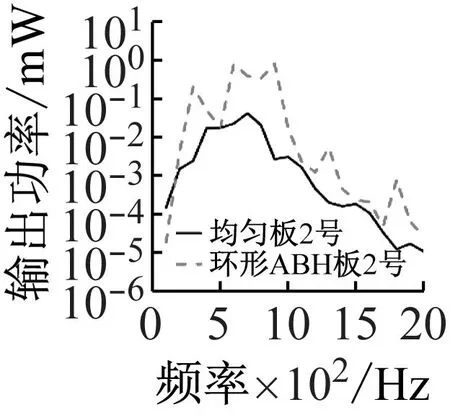
(b) PZT2
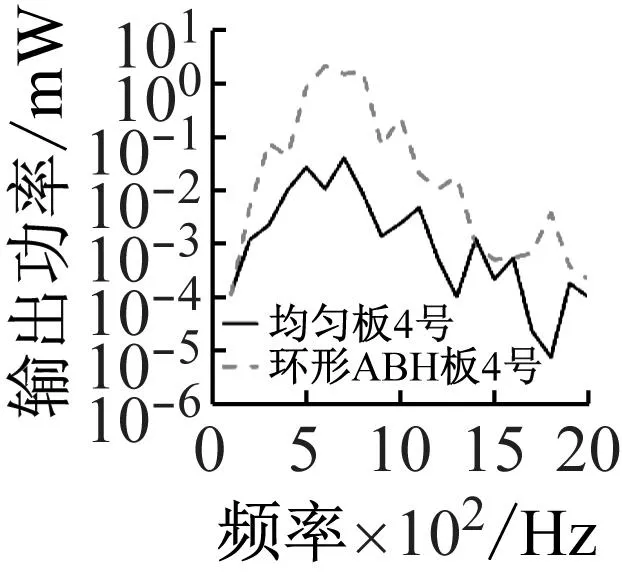
(c) PZT4图16 输出功率:环形ABH板与均匀板Fig.16 Output power: annular ABH plate and uniform plate
按照图14(a)中振动台控制软件设置的理论位移依次进行定频仿真测试,并将结果同试验结果进行对比。其结果如图17所示。仿真和试验数据在趋势上可以较好地吻合,特别是在0~900 Hz;在900 Hz之后,两条曲线的趋势仍然保持一致,但是两者的误差明显增大,这是因为此时振动台的理论输出位移非常小,由于设备安装精度造成的微小差距对实际激振效果的影响被放大,进而导致输出结果的差异。
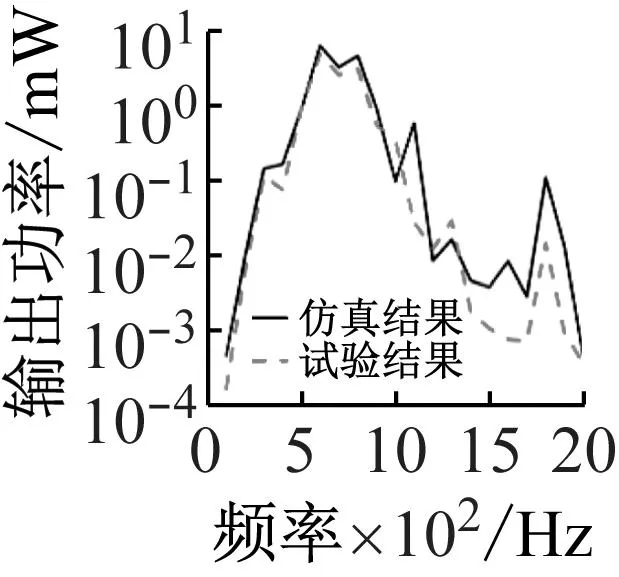
(a) PZT1
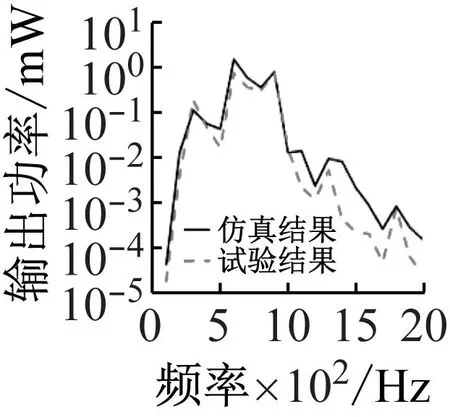
(b) PZT2
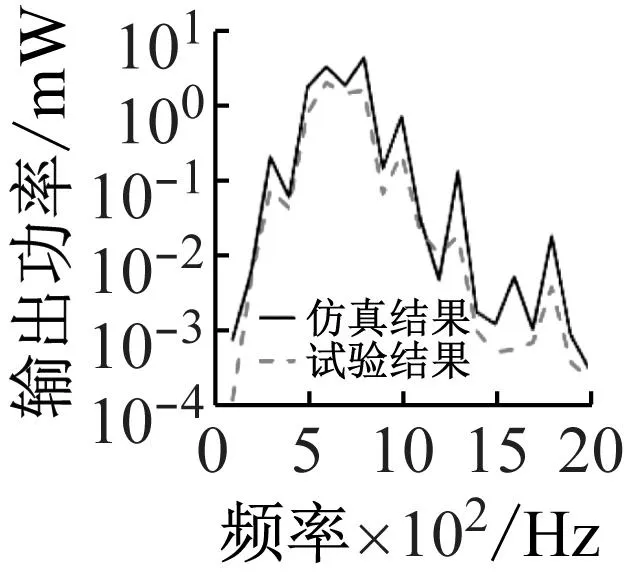
(c) PZT4图17 环形ABH板仿真与试验数据对比Fig.17 Comparison of simulation and test data of annular ABH plate
4 输出特性影响因素分析
通常情况下,较大的压电片面积有利于收集更多的能量,但在应用ABH进行能量收集时,还需要考虑其他因素。现有研究表明,在ABH中添加任何额外的结构都会影响ABH结构的能量集中效应,而且这种负面影响非常明显。因此,我们希望在两者之间找到一些最优的解决方案,使压电片及其附属装置对ABH效应本身的影响最小化,同时收集更多的能量。本文设计了不同几何尺寸的压电片,其宽度为bABH=10.00 mm,厚度为hABH=0.31 mm。仍然使用2.1节中的调制高斯信号作为激励源,取最小波长的5%~75%作为长度lABH的范围。图18(a)为lABH=7.35 mm时的瞬态响应输出功率,图18(b)为该时间范围内的能量输出,图18(c)为相同激励下不同尺寸压电片在0~10 ms内的能量收集情况。
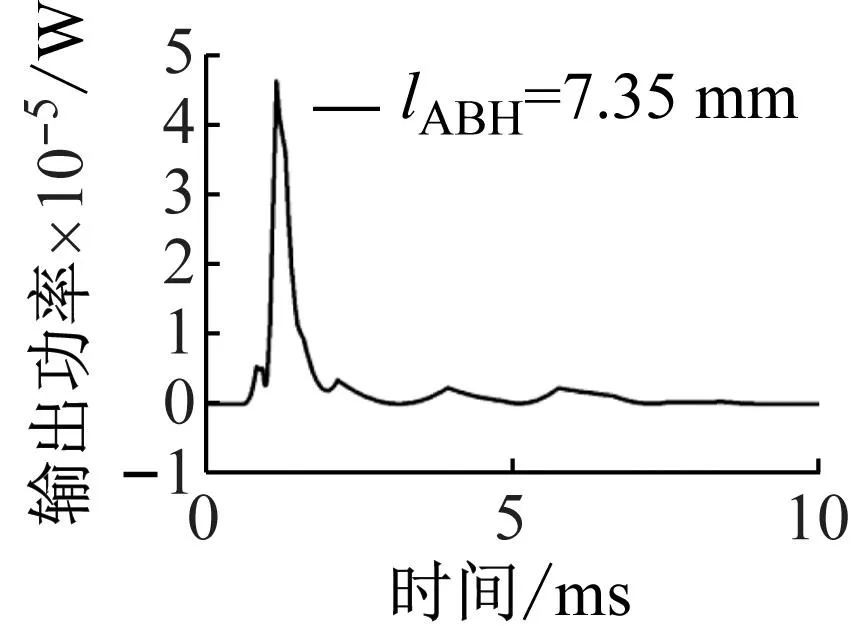
(a) 输出功率
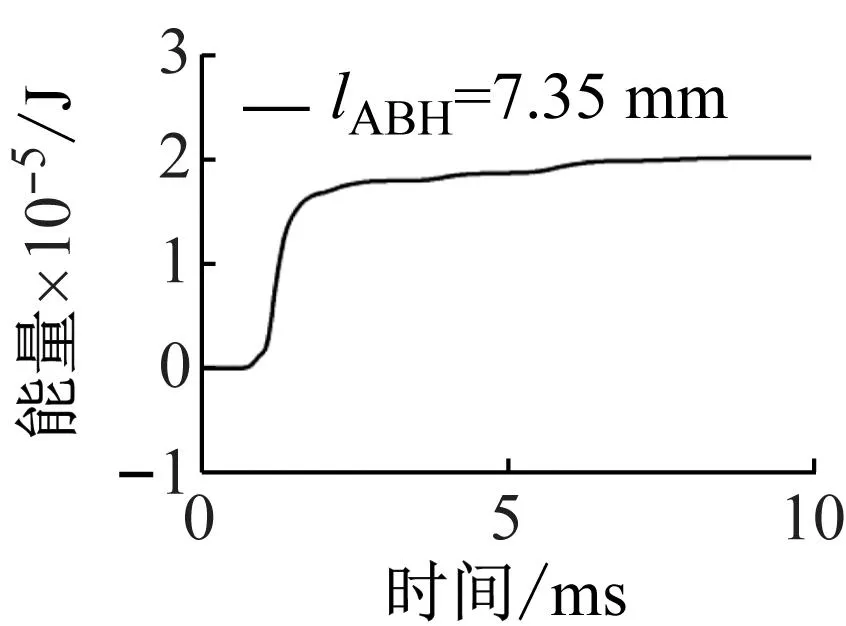
(b) 能量
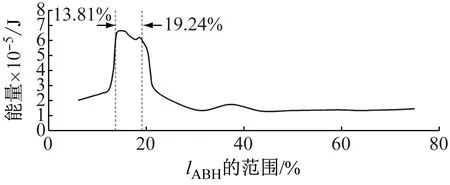
(c) 不同尺寸压电的输出能量图18 lABH=7.35 mm时输出功率、能量和不同尺寸压电片的输出能量Fig.18 When lABH=7.35 mm, output power, energy and output energy of different size PZT
采用改进的贝塞尔法对数据点进行拟合,得到图18(c)所示曲线。在最小波长的13.81%~19.24%范围内,10 ms内收集的能量超过6×10-5J,远高于其他区域。在设计压电能量收集装置时,压电片的几何形状应分布在此范围内,以获得更高的能量收集效率。
为了研究各种因素对输出电能E的综合影响,设计了四因素五水平的正交试验。试验值如表5所示。根据所设计的正交表进行了试验,其试验结果如表6所示。
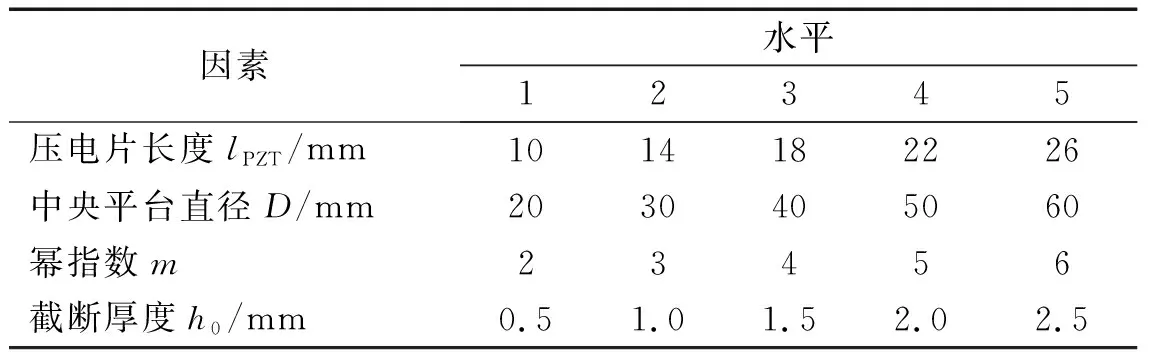
表5 正交试验的因素与水平Tab.5 The factors and levels of orthogonal test
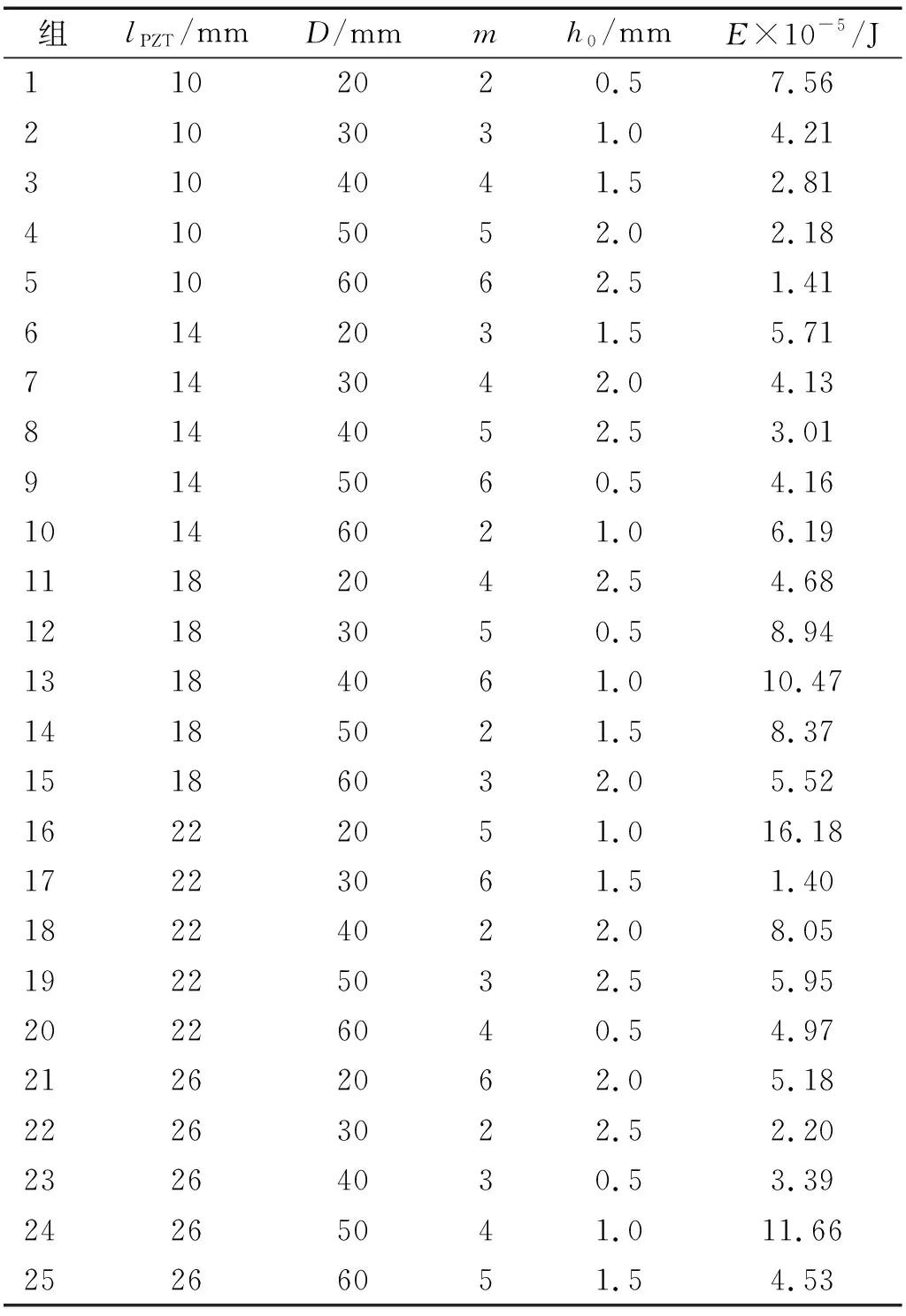
表6 多因素分析结果Tab.6 The results of multivariate analysis
采用极差分析各个参数对四项指标的影响,分析结果如图19所示。
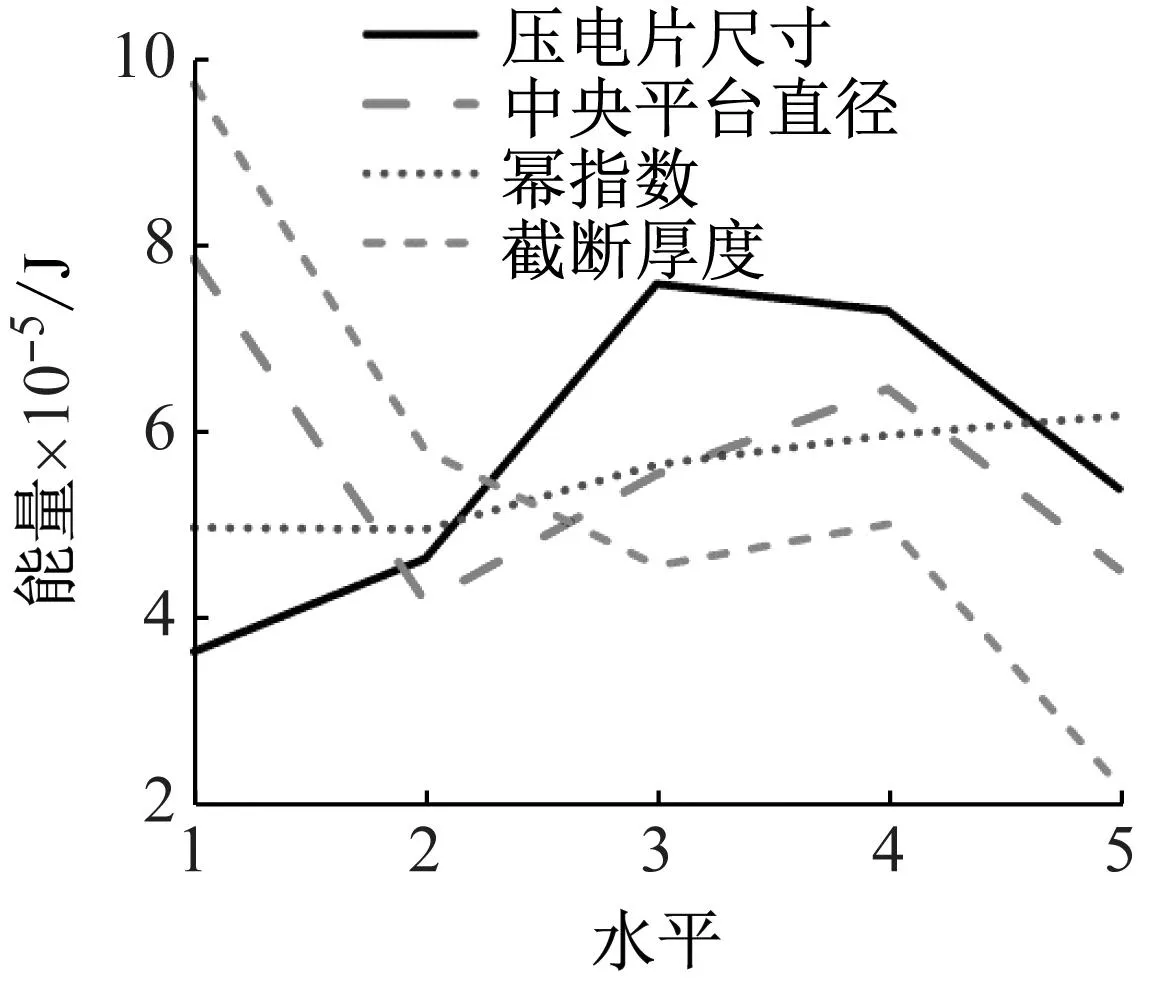
图19 极差分析结果Fig.19 The results of range analysis
由极差分析结果可得,四个因素对输出电能的影响显著程度排序为:截断厚度>压电片尺寸>中央平台直径>幂指数。根据试验结果对各参数重新组合,得到一组最优参数,并对其进行验证。结果如表7所示。

表7 优化结果Tab.7 Optimization results
5 结 论
本文对所设计环形ABH能量收集器进行了数值和试验研究。建立了环形ABH板与压电片及外部电路之间的机电耦合关系,研究了环形ABH板的压电能量收集性能,并通过试验验证了总结出的规律的正确性。主要结论总结如下:
(1) 环形ABH能量收集器可以将振动能量集中并高效收集,将高频率低振幅振动转化为便于收集的高振幅振动,并且在非共振频率下仍有较好的性能。
(2) 与传统的二维ABH结构相比,环形ABH结构具有更好的能量收集效率和更高的结构强度。
(3) 为了研究附加结构对ABH效应的影响,设计了一系列不同长度的压电片,其中在最小波长13.81%~19.24%范围内收集的能量远高于其他区域。
(4) 设计正交试验,通过多因素分析,以揭示所设计能量收集器各参数之间的相对重要性,并根据试验结果得出了具有最佳输出性能的参数组合。

