模块化建筑阵列多调谐质量阻尼系统的实现与减震研究
何晴光, 张释佺, 朱前坤, 洪祺凯
(1.兰州理工大学 甘肃省土木工程防灾减灾重点实验室,兰州 730050;2.西部土木工程防灾减灾教育部工程研究中心,兰州 730050)
作为一种最简单的被动振动控制器,单调谐质量阻尼器(single tuned mass damper,STMD)起源于1909年,Frahm[1]使用质量块和弹簧控制船舶的横摇运动,此装置能够在单一频率激励时将结构振幅减小至接近于零。随后Ormondroyd[2]使用弹簧与黏滞阻尼器并联的技术,在一定程度上拓宽了STMD的工作频带,提高了其对激励频率的鲁棒性。但随着研究的深入,Tuan等[3]通过对台北101大厦的STMD进行研究,发现该装置在风荷载下是有效的,而在远场地震作用下却并不有效。Domizio等[4]的研究表明,在近断层地震激励的主要频率明显高于结构基频时,STMD会失去作用。在地震作用下,STMD并不总是有效是因为地震激励往往是脉冲的,并且其频率成分较多,能够激起结构第一阶和更高阶模态的振动[5-6]。
1980年,Ayorinde等[7]将多调谐质量阻尼器(multiple tuned mass dampers, MTMDs)的概念引入土木工程领域。Bakre等[8]针对谐波激励下的单自由度结构,讨论了1~20个质量块的MTMDs的效率,研究表明其比STMD具有更强的鲁棒性。倪铭等[9]综合考虑成本和调谐效果,提出了一种双调谐质量阻尼器。Anajafi等[10]定量分析了分布式多重调谐质量阻尼器(distributed multiple tuned mass dampers, d-MTMDs)的鲁棒性,发生偏移的量包括主结构刚度、调谐频率比和作为激励的滤波高斯白噪声的频率,并采用遗传算法对d-MTMDs质量块位置参数进行优化。Elias等[11]对比分析了采用多模态控制技术设计的d-MTMDs的效率。
为解决附加质量导致的安全问题和成本问题,一些研究人员提出隔离楼板系统(floor isolation system,FIS),使用隔离楼板充当调谐质量阻尼器(tuned mass damper,TMD)质量块。Bin等[12]研究了在强震作用下,非光滑非线性的FIS中,主结构和隔离楼板之间动态耦合的影响。Casagrande等[13]对比了使用黏滞阻尼器和形状记忆合金阻尼器的FIS的有效性。Xiang等[14-15]研究了使用黏弹性层合材料隔离楼板对单层与双层钢框架结构振动控制的有效性和可行性。
同时,一些研究者对TMD的优化设计方法做出了创新和改进。Salvi等[16]研究了减震STMD性能和结构模态参数的关系,分析了TMD对结构模态的影响,并基于此提出一种分裂有效模态质量平衡的设计理念。Miyamoto等[17]基于线性矩阵不等式形式,提出STMD的鲁棒性设计方法,研究表明此方法设计的STMD系统对结构质量、刚度和阻尼的不确定性具有良好的鲁棒性。Ozturk等[18]为优化d-MTMDs质量块的位置参数,提出微分进化方法。
在大多数MTMDs的研究中,出于成本或安全性的考虑,每层仅布置一个质量块。涉及单层布置多个质量块的研究同样存在局限:①仅讨论了谐波激励;②仅讨论了单自由度的主结构;③仅讨论了质量块数量为20个以内的情况。
本文提出模块化悬挂楼板体系(modularized suspended floors system, MSFS)的概念,每个建筑模块内采用悬挂的方法将楼板与主结构隔离。该类建筑体系能够方便、安全的在每个楼层设置多个TMD对主结构进行调谐。因此,补充研究每层布置20个以上质量块的MTMDs的减震性能是必要的。同时本文提出了将振动控制装置与建筑共同模块化的思想,并基于此开展研究。
1 MSFS的建模
单个悬挂楼板模块的构造如图1(a)所示:悬挂楼板一方面通过弹簧和黏滞阻尼器与模块主结构的地板梁相连;另一方面通过吊索与模块主结构的天花板梁相连。采用这种构造的优点是:①悬挂楼板可以作为质量块发挥TMD的功能,对主结构进行调谐;②与使用隔振垫分隔楼板和主结构相比,这种构造既不会减少建筑使用高度,又使得楼板具有自复位能力。
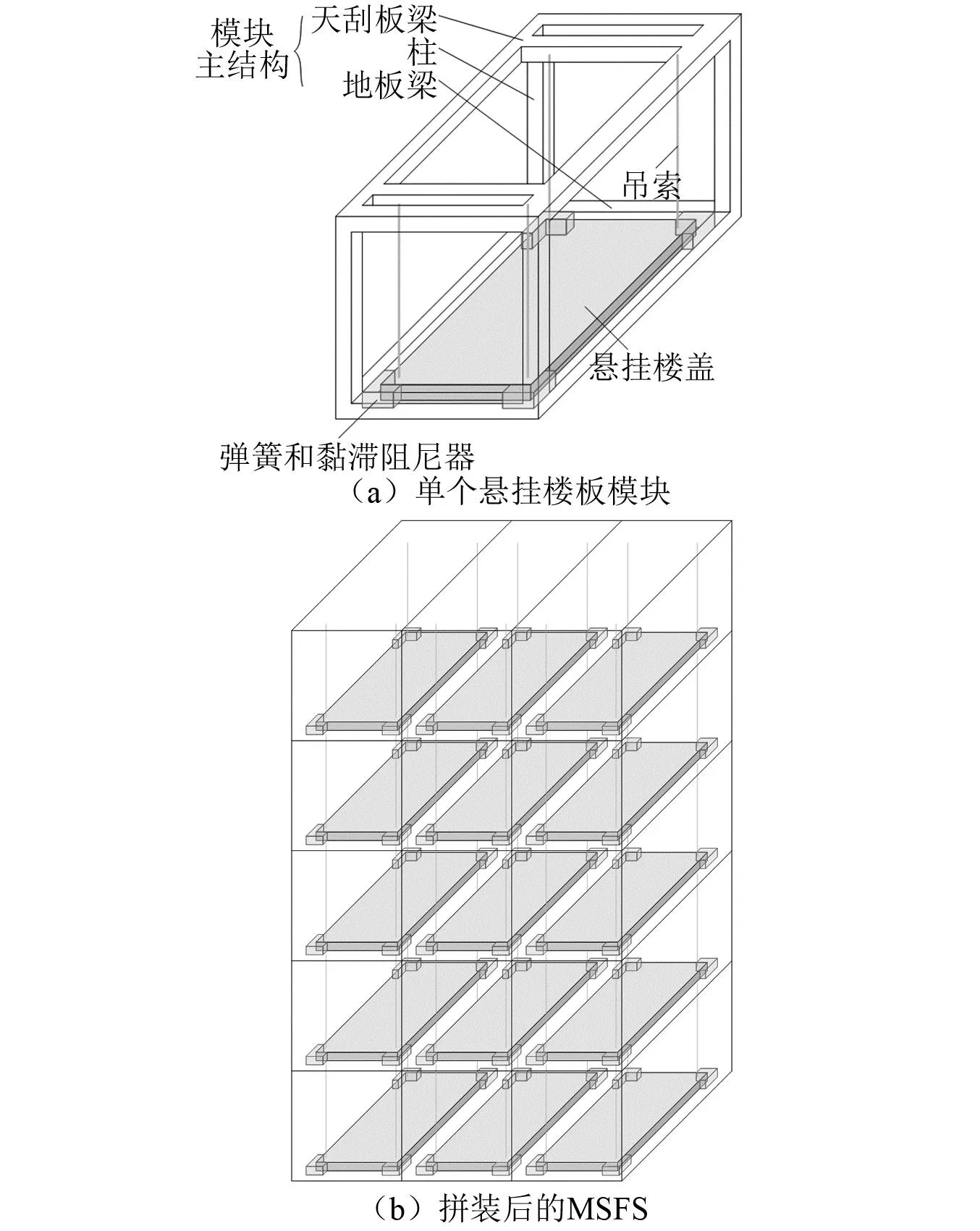
图1 MSFS的构造Fig.1 Construction of MSFS
将多个模块拼装成MSFS,如图1(b)所示。模块化的建筑单元在工厂预制后,运输到施工现场直接拼装。采用这种建造方式的优点包括:①施工方便,周期短,节约人力;②在工厂设置TMD的调谐频率比在施工现场更加准确。本文采用MSFS实现减小主结构振动的原理,仍然是基于将MSFS视作MTMDs系统。当结构面临危险的振动时,允许用悬挂楼板动力响应的增加,换取主结构动力响应的减小。但是,MSFS与仅顶层布置MTMDs或与应用了多模态控制技术的d-MTMDs相比,其最显著的特点是,能够将数量更加庞大的TMD方便、安全地布置在每个楼层,进而将原本较大的调谐质量,离散地分配到更多的调谐频率上,形成质量线性或非线性分布的调谐频带。基于此,本文提出分布阵列多调谐质量阻尼器(distributed array multiple tuned mass dampers, d-array-MTMDs)的概念,用来描述d-MTMDs模块化和空间分布的特征。
为解决楼板周边缝隙的防水、保温和隔音问题,MSFS系统在建筑上采用的处理方案如图2所示。其中,防水膜需要伸入盖板下部固定。然后,再将防水透气膜、保温材料、防潮隔气膜依次固定在盖板下部,膜边缘预留一定宽度后,固定于悬挂楼板外缘。
当悬挂楼板摆动到最大位置时,摩擦材料接触盖板,限制悬挂楼板的位移。当维修弹簧和阻尼器时,取下螺栓,打开盖板进行作业。
本文重点研究装有d-array-MTMDs的结构体系在水平方向上的振动问题,体系的离散质量模型如图3所示。对于楼板竖向荷载的传递方式,仅简单讨论图1(b)所示的上承式d-array-MTMDs的吊索对主结构和悬挂楼板水平位移响应幅值的影响。
本文中,下标“s”为主结构,下标“T”为TMD。图3所示的d-array-MTMDs,设共有p个TMD,编号用下标“i”表示,主结构共有N层,编号用下标“j”表示。根据图3所示的离散质量模型建立装有d-array-MTMDs的结构体系的运动方程,见式(1)。
(1)
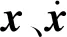
(2)
(3)
(4)
式中:ms、cs和ks为主结构的质量、阻尼和刚度矩阵;mT,i、cT,i和kT,i为第i个TMD的质量、阻尼和刚度;ai和bi为第i个TMD的位置向量,见式(5)~式(6)
(5)
(6)
式中,loci为第i个TMD布置的楼层,物理意义为第i个TMD通过弹簧和黏滞阻尼器与第loci层主结构相连。
本文采用逐步增量法求解体系的动力响应,流程如图4所示。
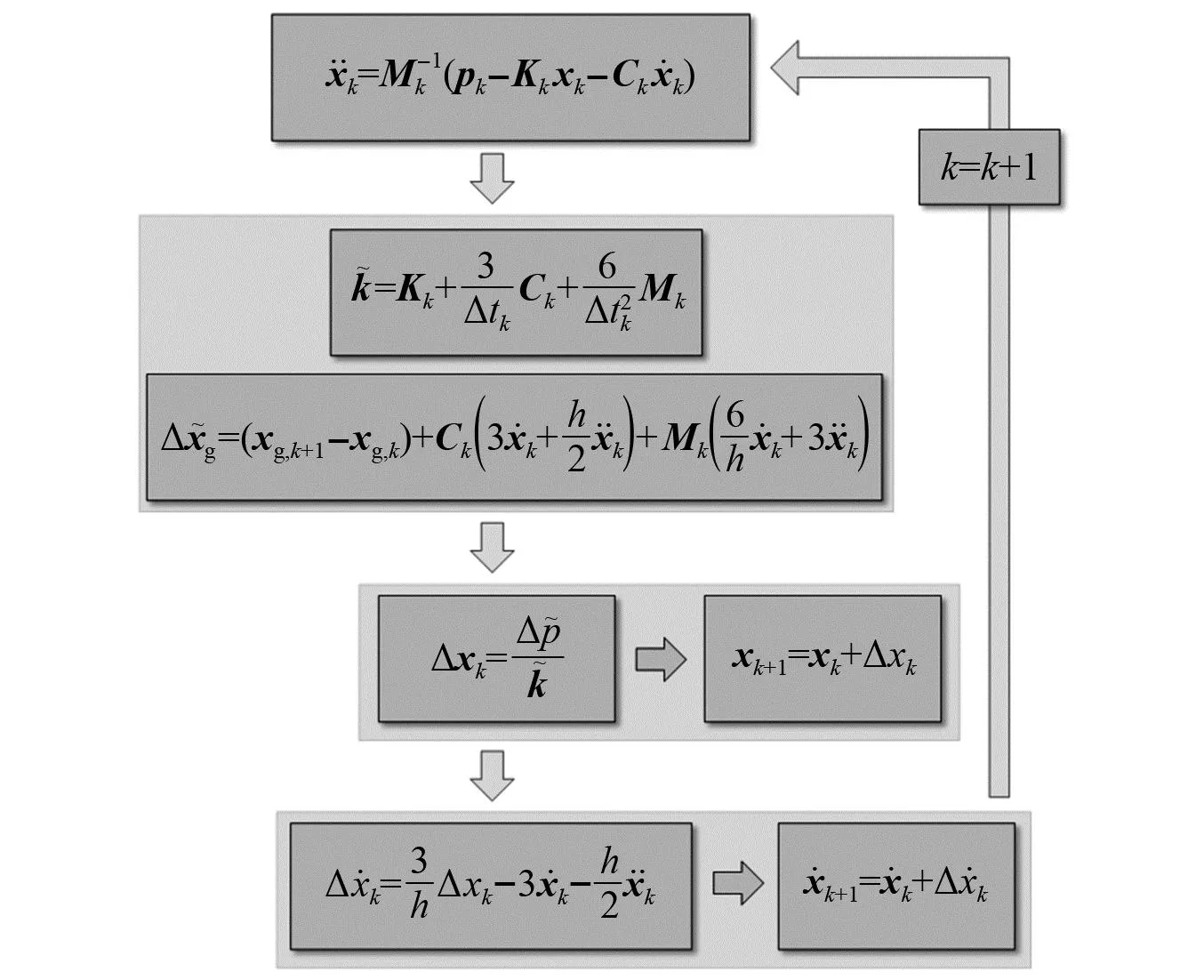
图4 逐步增量法计算流程Fig.4 Step by step incremental method calculation process
图4中:下标“k”为增量步编号,其下限为0表示体系的初始状态,上限为地震动记录的采样点数量;h为增量步的时间步长,由地震动记录给出。
2 悬挂楼板模块建筑的减震效果
2.1 目标函数与d-array-MTMDs系统的参数配置
为优化d-array-MTMDs的参数,将主结构各层间位移的均方根之和作为减震的结构响应指标和目标函数,见式(7)
(7)
式中:下标“c”为受控结构;下标“u”为作为参照的非受控结构。本文研究的d-array-MTMDs体系将楼板作为控制器的质量块。因此,非受控结构中,每层主结构的质量等于受控结构中该层主结构的质量与布置在该层的TMD的质量之和,见式(8)。
(8)
地震激励能够激起结构高阶模态的振动,导致调谐单一频率的STMD的振动控制效果不佳。因此,考虑将同样的调谐质量分配到近似连续的频带内。为了减少d-array-MTMDs的设计参数,每个楼层都布置数量相同的TMD。这样,d-array-MTMDs在每个楼层仅包含4个设计参数:平均调谐频率比η、调谐频带宽度系数β、TMD数量n以及调谐阻尼比ζT。其中,平均调谐频率比η和调谐频带宽度系数β的定义见式(9)~式(12)
(9)
(10)
(11)
(12)
式中:ωs,φ为主结构第φ阶振型频率;ωs,ave为主结构各阶振型频率的平均值;ωT,i为第i个TMD的调谐频率;ωT,ave为楼层各TMD调谐频率的平均值;η、β、n以及ζT作为自变量,通过Bakre等提出的线性插值公式计算每个TMD的调谐频率ωT,i,见式(13)。
(13)
式中,i的取值范围为[1,n]。进一步计算各TMD的阻尼系数cT,i和刚度系数kT,i,见式(14)~式(15)
cT,i=2mT,iζT,iωT,i
(14)
(15)
本文使用式(14)中的调谐阻尼比ζT表征TMD的阻尼系数水平。
质量比μ为各楼层TMD质量之和与主结构质量的比值,通过对图1中的构件质量计算,本文质量比取μ=0.5,各个TMD取相同质量mT,i通过式(16)计算。
(16)
综上可知,当n增大时,d-array-MTMDs调谐的频率点增加,而调谐各个频率点的TMD质量减小。
本文中,非受控结构每层质量取2×107kg、刚度取3.36×107N/m,每个模态的阻尼比取0.02。此外,考虑到柱承重的模块建筑高度的限制,讨论多自由度主结构时,结构层数最大取20层。
2.2 初步分析
建立一个两层结构,每层由3个模块组成。模块参数根据刘洋等[20]的研究选取,主结构的一阶振型频率为7.796 Hz。忽略吊索影响时,结构中只有二层的悬挂楼板对一层主结构具有调谐作用,其中一个悬挂楼板调谐主结构一阶振型频率,另外两个调谐弹簧刚度在其基础上±50%。主结构和悬挂楼板的阻尼比均取0.02。3个悬挂楼板按照调谐频率从低到高分别命名为T1-1、T1-2和T1-3
输入谐波激励进行频域分析,见图5。激励频率等于主结构一阶振型频率。
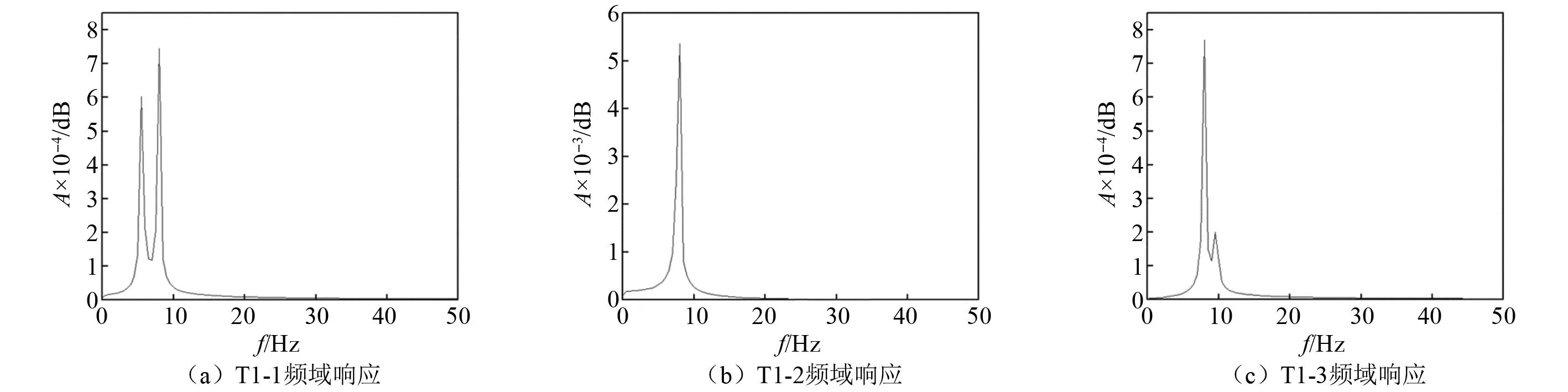
图5 悬挂楼板频域响应Fig.5 Frequency domain response of suspended floors
根据图5可知T1-1和T1-3的位移响应包含两个频率成分,T1-2仅包含一个频率成分,图5中峰值点对应的频率见表1。
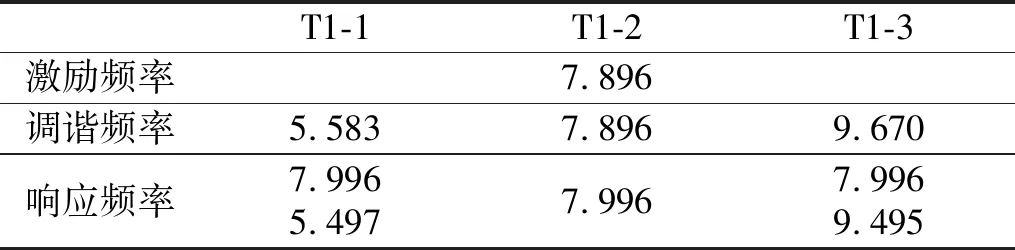
表1 峰值频率Tab.1 Peak frequency 单位:Hz
频域分析表明,结构响应的频率成分包括了激励频率和结构固有频率,并且激励频率(结构一阶振型频率)占主导地位。
考虑到悬挂结构的自振周期一般较长,采用两条频率成分集中在低频段的经典地震动记录作为激励进行初步参数分析。选用激励见表2,其傅里叶谱如图6所示。

表2 地震动记录Tab.2 Ground motion record
图6 激励傅里叶谱Fig.6 Fourier spectrum of excitation
主系统选择单自由度体系,采用图7所示迭代流程对平均调谐频率比η、调谐带宽系数β、TMD数量n以及调谐阻尼比ζT4个参数进行初步分析。根据No.1和No.2地震激励下图8的计算结果,初步确定d-array-MTMDs的基本参数见表3。

表3 d-array-MTMDs参数取值
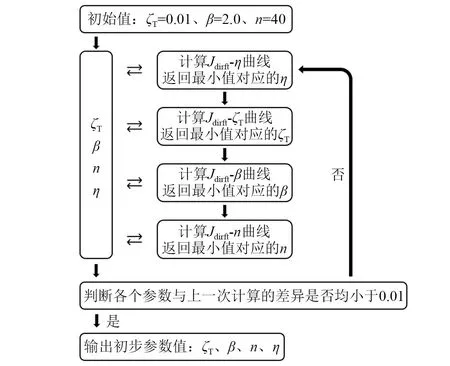
图7 迭代流程Fig.7 Iterative process

图8 SDOF-FIS体系初步参数研究Fig.8 Preliminary parameter research of SDOF-FIS system
迭代过程中,以各个参数的数值误差均小于0.01作为退出循环的条件。
图8(a)表明,当输入不同地震波时,使体系有较好减震效果的η取值不完全相同,但是,当η的取值大于最优值后,目标函数增幅较小且趋于稳定。此外,当η在某些区间内时,d-array-MTMDs对单自由度主结构可能是有害的。
图8(b)表明,ζT的变化对目标函数影响很小,虽然较大的阻尼比会对调谐频率产生一定影响,但是Anajafi等的研究表明MTMDs系统较大的阻尼比会降低体系对结构和激励不确定性的敏感度,使控制系统具有更强的鲁棒性,因此在设计d-array-MTMDs时仍然建议条件允许时采用较大的调谐阻尼比。图8(c)表明,当β取较大值时,d-array-MTMDs的控制效果显著提升。结合式(10)可知,工作频带较宽的d-array-MTMDs具有更好的控制效果。同时,地震激励不同时,d-array-MTMDs的减震效果在相同的β取值时,仍然存在明显差异,这表明d-array-MTMDs需要调谐的频率不仅是主结构固有频率,还应当考虑地震激励的频率成分。
图8(d)表明,在n较小时,d-array-MTMDs的减震效果对n值的变化和地震激励较为敏感,当n大于20后,d-array-MTMDs的减震效果几乎不随n发生变化,表现出稳定且良好的减震性能,可以认为对于模块化建筑应该存在TMD的充分数量值,或者说,布置超过某一数量的TMD带来的边际效应并不明显。
由于d-array-MTMDs中每个TMD的调谐频率均由线性差值确定,故当TMD数量改变时,d-array-MTMDs调谐的频率,除ωT,1和ωT,n外,均发生改变。因此,在图8(d)中,当n小于20时,曲线的波动现象表明,只有当d-array-MTMDs调谐到特定频率时,才会有较好的减震效果。而当n大于20后,曲线的稳定现象则表明,d-array-MTMDs对其调谐频率小范围邻域内的振动同样具有抑制作用。
初步分析对后续分析提出了以下建议:
(1)平均调谐频率比η在[0, 2.5]内进行讨论,调谐频带宽度系数β在[0, 2]内讨论,调谐阻尼比ζT在[0, 0.5]内讨论,TMD数量n在[0, 6]内讨论。
(2)应当注意调谐频率点的离散程度对Jdrift曲线的波动现象的影响。
(3)Jdrift曲线的稳定可能与TMD数量n、调谐阻尼比ζT以及调谐频带宽度有关,需要进一步研究。
2.3 MSFS中吊索的影响
在MSFS中,体系动力方程的变化出现在式(4),见式(17)
(17)
式中,bv,i为第i层吊索的位置向量
(18)
式(17)中的kv,i为第i层吊索的等效刚度,计算方法由单摆模型给出
(19)

Δ(·)=(·)Ti-(·)s(loci-1)
(20)
式(19)表明,kv,i为时间t的函数,这导致式(1)中的矩阵K也是时间的函数,对式(1)进行拉普拉斯变换将更加复杂。因此,本文采用逐步增量法求解体系响应,在每一个增量步开始前,通过体系上一个增量步的位移、速度和加速度重新计算kv,i,更新刚度矩阵后,再进行下一个增量步的计算。
取吊索长度l=3 m,此时吊索长度对应的楼板复位等效刚度约为单个模块主结构侧向刚度的0.3%,换算成调谐频率比为Δη= 0.077。主结构自由度N=2,TMD布置数量n=1,位置loci=1,η、β和ζT采用表3取值。
分别对包含吊索的MSFS与不包含吊索的FIS输入No.1和No.2地震激励,对比主结构和次结构响应的位移时程曲线,如图9所示。

图9 FIS系统与MSFS系统的动力响应对比Fig.9 Comparison of dynamic response of MSFS and FIS
图9显示,当l=3 m时,包含吊索的MSFS与不包含吊索的FIS对比可见,两者振动响应区别较小,且吊索长度对次结构的影响略大于主结构。为MSFS定义指标Jv定量地考察吊索在结构振动过程中提供的恢复力的大小,见式(21)。
(21)
式中,xs,0为地面位移,因本文动力方程选择了地面为参考系,故在任意时刻都有xs,0=0。对No.1和No.2地震激励计算Jv,得到在两次地震下吊索提供的恢复力分别为主结构框架恢复力的18.88%和22.99%。由此可知,当主次结构的质量比为μ=0.5时,吊索提供的恢复力不宜忽略,结合吊索等效刚度的数量级可知,悬挂楼板的相对位移较小时吊索提供的恢复力也较小。本文重点是研究d-array-MTMDs的调谐性能,因此,将吊索长度取为常数后,将FIS和MSFS统一起来进行讨论,TMD布置位置loci在[1,n]内取值。
3 参数分析
初步分析表明,调谐阻尼比和调谐带宽系数的设计值较为明确,而TMD数量和平均调谐频率的设计值与主结构以及地震激励的频率成分有关。因此,将初步分析的部分工作扩展到多自由度主结构,并引入更多地震动记录作为激励是有必要的。本章使用表4所列的地震动记录作为激励,针对平均调谐频率比η、TMD数量n和主结构层数N3个参数进行分析。
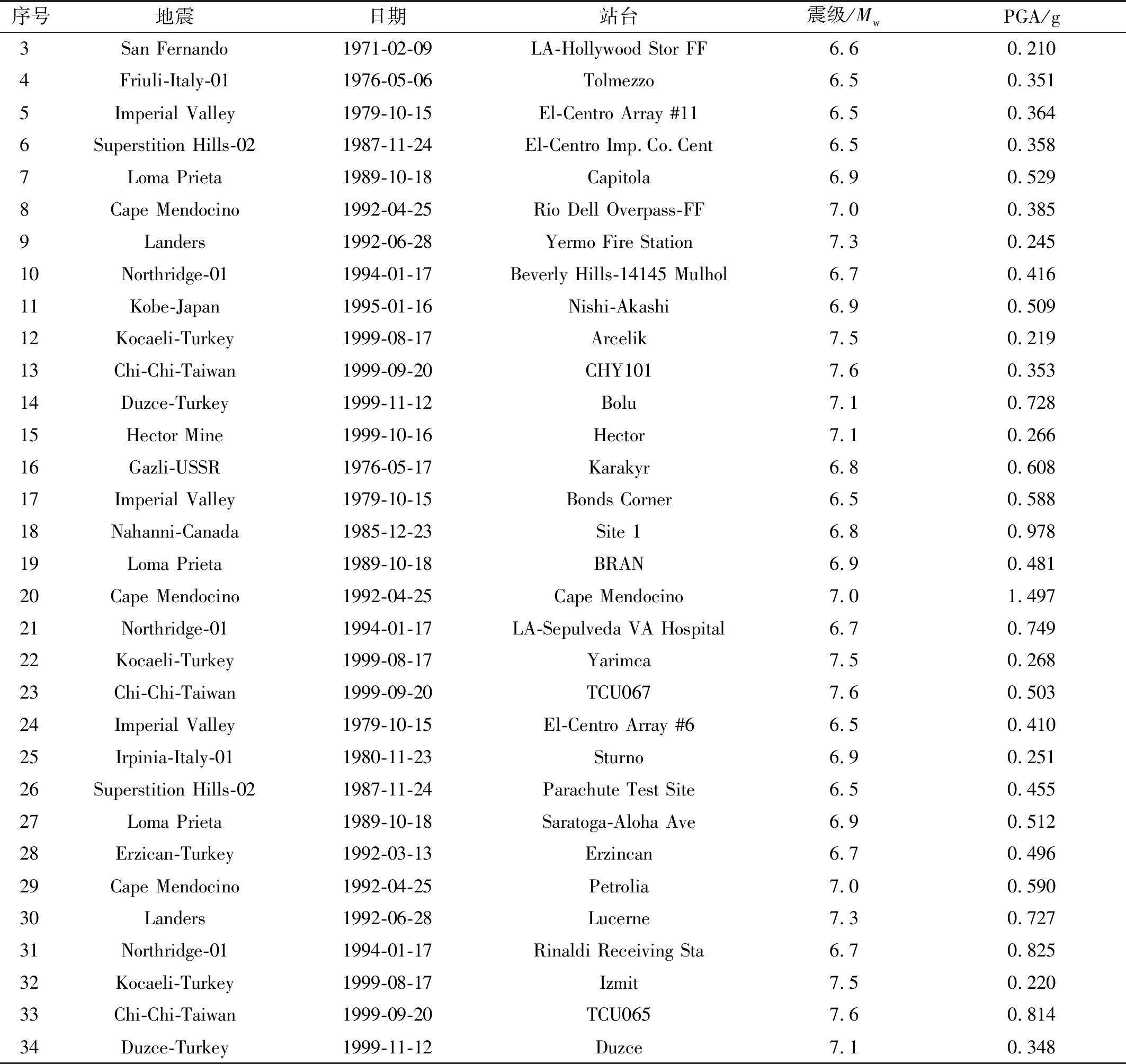
表4 地震动记录Tab.4 Ground motion record
表4中, 3号~15号为远场地震, 16号~23号为近场非脉冲地震,24号~34号为近场脉冲地震。首先对η分析,随后按照分析结果取最优值。
参数ζT、β、n和N不作为自变量时取值见表5。

表5 d-array-MTMDs参数取值Tab.5 Specifies the value of the parameter of d-array-MTMDs
平均调谐频率比η在0~2.5内变化时,结构在远场、近场非脉冲和近场脉冲型地震激励下的响应如图10所示。

图10 不同地震类型下三层主结构响应随η的变化规律Fig.10 Variation of main structure response of three storeies with η under different earthquake types
图10表明,在不同类型的地震作用下,随着η增大,主结构响应均呈现先减小后增大的趋势,曲线的下降段比上升段更加陡峭。d-array-MTMDs的η过小可能会对主结构产生不利影响,最优取值范围为η∈[0.7,1.0]。
当η小于最优值时,d-array-MTMDs的控制效果在近场脉冲型地震作用下最好,远场地震下次之,近场非脉冲型地震下最差,当η大于最优值时,d-array-MTMDs的控制效果在近场非脉冲型地震作用下最好,远场地震下次之,近场脉冲型地震下最差,并且此时主结构响应曲线的增幅趋于平缓,这表明选择较大的η作为设计值,d-array-MTMDs的减震效果更加稳定。
在32次地震激励下,将装有d-array-MTMDs的结构平均响应与每层布置一个TMD的普通MTMDs以及非受控体系进行对比,结果如图11所示。
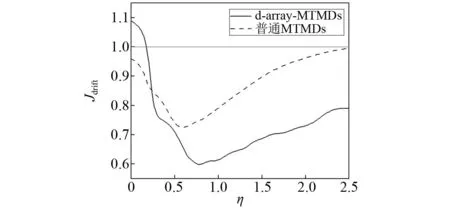
图11 d-array-MTMDs与普通MTMDs系统的对比Fig.11 Comparison between d-array-MTMDs and common MTMDs
图11表明,安装了d-array-MTMDs的结构位移响应平均减少40%,比使用每层布置一个TMD的MTMDs效果更好,这表明将有限的调谐质量分配到更多的调谐频率上的做法是可取的。选择图11中结构响应最小值对应的平均调谐频率值η=0.781,计算结构响应随TMD数量n的变化规律,如图12所示。

图12 不同地震类型下三层主结构响应随n的变化规律Fig.12 Variation of main structure response of three storeies with n under different earthquake types
图12表明,由图8(d)得到的结论可推广到多自由度主结构的情形。随着TMD数量的增加,结构响应曲线呈现出从不稳定逐渐稳定的规律。虽然在不同地震激励下,系统达到稳定状态所需的TMD数量存在较为明显的差异,但绝大多数地震激励下,系统可以在TMD数量大于20个的条件下达到稳定状态。因此,在采用质量比为μ=0.5的d-array-MTMDs控制结构振动时,建议每个楼层布置的TMD的数量大于20个。同时,在图12(a)~图12(c)中,一些地震激励在n=20时还未达到稳定状态,这解释了图10中,当η取较大值时,一些曲线出现的波动现象。
此外,图12(d)表明,d-array-MTMDs在TMD数量n变化的过程中,在远场、近场非脉冲和近场脉冲3种类型的地震激励下具有近似相同的减震效果。为了更深入地讨论d-array-MTMDs系统稳定状态所需的最小TMD数量nmin的影响因素,还需要补充nmin与η和ζT的关系。基于控制变量法,选取图10中波动现象最明显的两条地震动记录18号和23号作为激励展开研究。经过试算,将n每增加10,Jdrift的变化范围小于0.02作为体系处于稳定状态的判据,定义此时的TMD数量为nmin。计算nmin随η和ζT的变化规律,如图13所示。
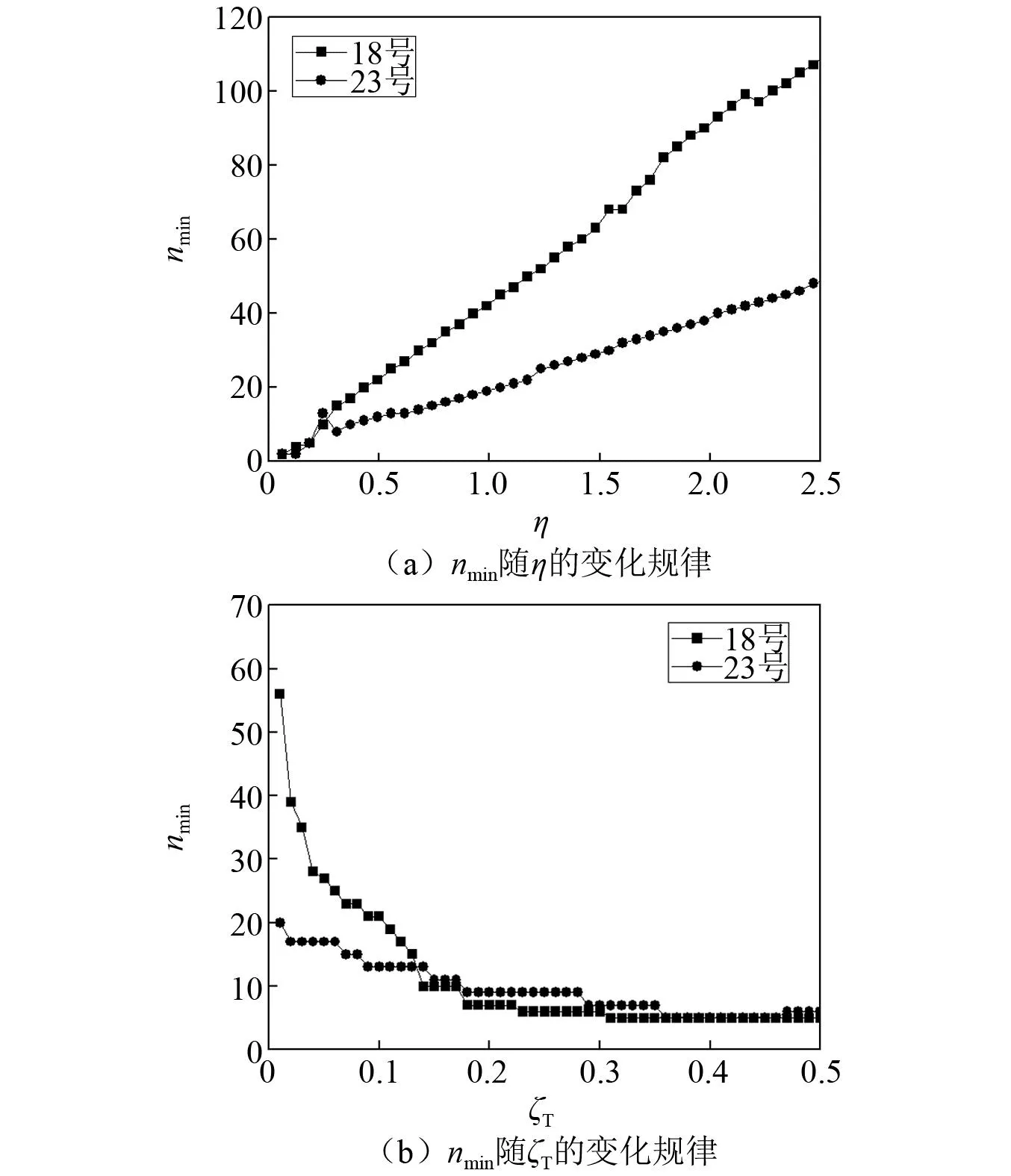
图13 nmin随η和ζT的变化规律Fig.13 Variation of nmin with η and ζT
图13表明,η在0~2.5内,nmin与η正相关,斜率与地震特性有关;ζT在0~0.5内,nmin单调递减。一方面,虽然选择较大的平均调谐频率比η能够在更多地震激励下,保持d-array-MTMDs较好的减震性能,但较大的η使系统需要更多TMD才能达到稳定状态,根据本文研究数据,建议η在0.7~1.0内取值;在另一方面,虽然较大的调谐阻尼比ζT可能小幅降低系统的减震效果,见图8(b),但却能明显减小系统稳定状态所需的TMD数量,故建议在成本允许的条件下,为d-array-MTMDs选取较大的ζT值。
除调谐参数外,为了避免d-array-MTMDs对主结构的作用力存在较大偏心距,不同调谐频率的TMD在建筑平面中的布置位置也需要被考虑。为此,在N=1、n=40并且忽略阻尼力作用的情况下,在时程分析的过程中用主结构受到的水平剪力对每个TMD对主结构的作用力进行归一化处理,建立量化指标JF,i如式(22)所示。
(22)
在3种类型的地震作用下,不同TMD对主结构的作用力JF,i如图14所示,其中TMD编号i与TMD调谐频率ωi成正比。

图14 d-array-MTMDs对主结构的作用力分布Fig.14 Force distribution of d-array-MTMDs on the main structure
图14表明,编号从0~20的TMD对主结构的作用逐渐增大,编号为21~25的TMD对结构的作用力出现一个峰值,编号为40的TMD对结构的作用力出现另一个峰值,编号为26~39的TMD对结构的作用力维持在略小于峰值的较高水平。d-array-MTMDs对主结构的作用力主要由调谐频率较大的TMD提供。
图14(d)表明,不同类型的地震作用下,d-array-MTMDs对主结构的作用力分布呈现一致的规律,其中,近场非脉冲型地震作用下,d-array-MTMDs对主结构的作用力分布在不同TMD之间的变化最剧烈,远场地震次之,在近场脉冲型地震作用下最平稳。
综上所述,在设计d-array-MTMDs时,宜优先将调谐频率ωi大于平均调谐频率ωT,ave的TMD均匀布置在建筑平面中,再布置调谐频率较小的TMD。若仅仅将TMD顺序排列在建筑平面中,会造成d-array-MTMDs对结构的偏心作用。
最后,研究主结构层数变化对d-array-MTMDs减震效果的影响。计算主结构从1层逐渐增加至20层的过程中,结构响应指标Jdrift随主结构层数N的变化规律,如图15所示。

图15 不同地震类型下主结构响应随N的变化规律Fig.15 Variation of main structure response with N under different earthquake types
图15表明,主结构层数的增加使d-array-MTMDs的减震效果逐渐趋于稳定,同时在20层以下,d-array-MTMDs均表现出平均减震48%的良好效果。此外,随着模块建筑层数的增加,d-array-MTMDs也能维持较好的减震效果,这表明d-array-MTMDs系统能够用于主结构层数较高的情况。
4 结 论
基于建筑的模块化,将普通MTMDs中的调谐质量分割并调谐到一定频带宽度内的多个频率点上,提出一种d-array-MTMDs方案,并对d-array-MTMDs进行参数分析得到如下结论:
(1)d-array-MTMDs系统的减震效果主要受平均调谐频率比η、调谐频带宽度系数β以及TMD数量n的影响,调谐阻尼比ζT和主结构层数N对系统减震效果影响较小。
(2)d-array-MTMDs系统的η建议在0.7~1.0内取值,当η小于最优值时,d-array-MTMDs的控制效果在近场脉冲型地震作用下最好,远场地震下次之,近场非脉冲型地震下最差,当η大于最优值时,d-array-MTMDs的控制效果在近场非脉冲型地震作用下最好,远场地震下次之,近场脉冲型地震下最差。
(3)当β取较大值时,d-array-MTMDs的控制效果显著提升,换言之,工作频带较宽的d-array-MTMDs具有更好的控制效果。不同地震激励下,d-array-MTMDs的减震效果在相同的β取值时,仍然存在明显差异。综合考虑,β建议取2.0。
(4)随着TMD数量n的增加,体系的减震效应会从不稳定状态变化到稳定状态,稳定状态下d-array-MTMDs的减震效果不再随n发生明显变化,并且在不同类型的地震作用下,结构减震效应呈现出高度的一致性。根据本文的研究,TMD数量建议取值为n>20。此外,达到稳定状态所需最少TMD数量nmin与η呈线性线性递增关系,与ζT呈非线性单调递减关系,故综合考虑,ζT建议在成本允许的范围内取较大值。
(5)d-array-MTMDs对主结构的作用力主要来自于调谐频率较大的TMD,故布置d-array-MTMDs中的TMD时,宜优先将调谐频率较大的TMD在建筑平面中均匀布置。
(6)主结构从1层增加至20层的过程中,安装了d-array-MTMDs的结构位移响应平均减小48%。同时,d-array-MTMDs系统更加适合但不局限于主结构较高的情况。

