网格吊索结构对拱桥强健性的影响分析

■邱宏彬

(福州路信公路设计有限公司，福州 350007)

0 引言

中、下承式拱桥一般由拱肋、横撑、吊杆和纵横梁桥面组成[1]。其中吊杆作为中、下承式拱桥的主要受力构件，主要的功能是通过吊杆自身的拉伸受荷，将桥面系上的荷载，传递到拱肋，由拱肋承载，因此拱桥的安全与吊杆的健康状况密切相关[2]。在现在中、下承式拱桥的建设中，吊杆越来越多地采用高强钢索(简称吊索)[3]。数十年来，桥梁拉索骤断乃至垮桥的实例，一直没有杜绝[4]。国内外统计表明，桥梁拉索的寿命不长，国内为3～16年[5]，很少超过20年，仅是桥梁设计时限的1/20～1/4。因此，在中、下承式拱桥的设计使用年限内，吊索有可能多次断裂或拆换。由于吊索构件的非永久性，《公路桥涵设计通用规范》(JTGD60—2015)[6]和《公路钢管混凝土拱桥设计规范》(JTG/TD65-06—2015)[7]都规定吊索为可更换部件，设计使用年限不应低于20年。有些早期设计的吊索往往达不到这个使用寿命。达到使用寿命时未及时更换，设计、施工和养护不当等引起的吊索腐蚀、疲劳以及交互作用引起的承载力下降未能及时发现、超重荷载、车辆碰撞等偶然事件等等，都可能导致吊索事故的发生。一些桥梁在发生吊索断裂之后，由于其自身的结构悬吊桥面系的强健性较弱，后续引起了桥梁结构的连续性破坏，造成桥面垮塌、交通中断，甚至严重的车毁人亡交通事故，如四川省宜宾市金沙江小南门桥[8]、攀枝花市金沙江大桥[9]等。

汤国栋[10]等针对吊索断裂问题，进行了破损安全桥梁拉索及其系统研究，提出了不同的吊索安全破损系统，并对吊索系统进行验算分析，讨论了需要换索的工况下受力性能。但该分析仅是静力作用，并未针对该类吊索进行断索模拟动力研究，若在使用过程中突发断索意外，无法判断拱桥是否有足够的强健性。

所谓强健性，即鲁棒性(Robustness)，它主要是指结构在遭受爆炸、火灾、冲击、罕见的强烈度地震、灾难性洪水、人为失误等极端事件时，不会造成损害与原始动因不成比例的能力。结构强健性设计，要求整体结构对局部破坏不敏感，且具有抵抗连续破坏的能力。当前的结构设计理念已从传统的“结构在设计荷载作用下不破坏”的安全性原则，向“结构在局部构件失效时，仍具有足够的整体牢固性”的强健性原则转变。

因此本文以一座下承式刚架系杆拱桥为对象，进行平行吊索与网格吊索断裂后，受力性能的分析与对比研究。

1 工程实例与有限元介绍

1.1 项目工程实例

图1为某下承式刚架系杆拱桥的设计，跨径为85m，矢跨比为1/5，拱轴线为二次抛物线。拱肋截面设计为哑铃型，高度为2.1m。拱肋弦管材料为Q345，规格采用900×14mm无缝钢管，管内填充C50混凝土。桥面宽度为3m人行道+1.5m纵梁+15m行车道+1.5m纵梁+3m人行道，其中拱肋间距为16.5m。设计荷载为公路一级，双向四车道。其立面图与平面图如图1所示。

1.2 有限元模型

图1 某跨径85m的下承式刚架系杆拱桥(单位：cm)

利用ANSYS/LS-DYNA显式动力分析程序建立试验缩尺模型的有限元模型进行分析计算，得到吊索断裂后，剩余拱桥结构的动力性能变化程度。目前在涉及到动碰撞、冲击等高度非线性的动力学问题时，大多数都使用LS-DYNA的显示分析程序，这是当前世界上最著名的显式动力分析程序。除显示分析外，LS-DYNA兼有隐式求解功能；因此即可分析动力问题，也可对静力问题进行计算。ANSYS/LS-DYNA将ANSYS前后处理器与LS-DYNA求解器结合，利用ANSYS建立几何模型，再用LS-DYNA求解，从而得到分析结果。

本文主要利用ANSYS/LS-DYNA中的接触碰撞处理的功能来实现吊杆的断裂。当柔性吊杆受到横向碰撞时，吊杆内力将会增加，通过控制碰撞体的速度，可以让吊杆内力在较短的时间内达到某一个最大值。吊杆内力的增大将对拱肋及桥面产生扰动的作用，导致拱肋及桥面产生一定的竖向冲击的作用，如果在碰撞过程中吊杆的内力达到某一个值时断裂，则相当于在对吊杆处施加了一个相应的断索冲击力的作用。

试验缩尺模型的ANSYS/LS-DYNA有限元模型采用Link167单元，质量采用Mass166单元，其余构件均采用beam161单元模拟。其中各材料的密度、弹性模量等实常数根据图纸取值。

为了更好地描述分析结果，将刚架系杆拱桥进行编号。对于吊索，以一侧拱脚短吊索到另一侧短吊索编号依次为11#～15#，一根横梁两端的吊索采用相同的编号，吊索所在的纵梁截面编号与吊索相同，编号见图1(a)。模型如图2所示。

2 吊索断裂方法与断裂吊索选取

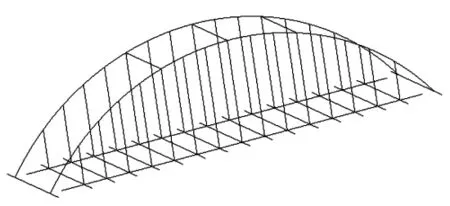
图2 有限元模型

文献[11]指出在进行中、下承式拱桥断索分析时，主要考虑长、短吊索断裂时全桥的受力状态。短吊索处于拱肋和系梁的交接区域，该区域受收缩徐变和升降温交替变化影响引起的变位最为突出，从而使得拱脚附近的短吊索相比长吊索更容易发生断裂的危险。但由于最短吊索在桥梁运营阶段往往以受弯矩破坏为主，内力较小，在最短索断裂时引起的剩余结构振动不突出。并且在发生过断索事故的工程中，主要是由于次短吊索断裂引起的，因此本文选取次短吊索断裂进行分析。吊索断裂对桥面的影响远大于拱肋，吊索断裂最不利吊索为与断裂吊索相邻的吊索，文献[11]还得出最不利纵梁截面为吊索断裂处的纵梁截面。因此本文仅对吊索断裂后的最不利剩余吊索与纵梁截面进行研究分析。

3 有限元结果分析

3.1 平行吊索

3.1.1 吊点位移

当吊索断裂时，断裂产生的能量第一时间由断裂吊点处的拱肋及桥面系共同承担。图3示出了吊索断裂时，断裂吊索处拱肋及桥面系吊点的位移时程曲线。其中位移以向上为正，向下为负。可以看出，2#吊索断裂时，桥面系最大位移为10.99mm，发生在断索后约0.91s，拱肋最大位移为5.01mm，发生在断索后约1.09s；纵梁位移与拱肋位移的比值为2.19。

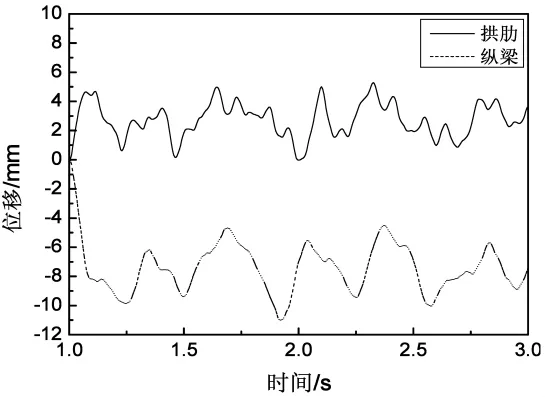
图3 2#断裂吊索吊点位移时程曲线

3.1.2 吊索

对于跨径85m下承式刚架系杆拱桥，在次短吊索断裂时的冲击荷载作用下，断裂吊索相邻3#吊索处于最不利的受力状态。图4给出了断裂短吊索相邻的3#吊索的轴力时程曲线。可以看出，3#吊索初始轴力为1315.24kN，在断索冲击作用下轴力最大值1784.09kN，发生在吊索断裂后约0.885s。轴力变化比为36.6%。

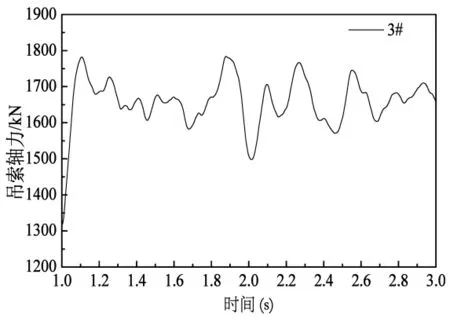
图4 3#吊索轴力时程曲线

3.1.3 纵梁

在次短吊索断裂时的冲击荷载作用下，吊索断裂处纵梁截面(2#)处于最不利的受力状态。图5给出了吊索断裂处纵梁截面(2#)的应力时程曲线。可以看出，吊索断裂处纵梁截面(2#)的初始应力为6.137MPa，在断索冲击作用下应力最大值为13.039MPa，发生在吊索断裂后约0.935s。应力变化比为112.5%。

图5 2#纵梁截面应力时程曲线

3.2 网格吊索

将该刚架系杆拱桥的平行吊索替换为网格吊索，替换规律为拱肋的n#吊点与(n+1)#，(n-1)#纵梁吊点连接，替换后的立面图如图6所示。断裂吊索选取连接3#拱肋吊点与2#纵梁吊点的吊索。

图6 网格吊索拱桥

3.2.1 断索吊点位移

图7给出了各个工况相应吊索断裂时，断裂吊索处拱肋及桥面系吊点的位移时程曲线。可以看出，2#吊索断裂时，桥面系最大位移为7.10mm，发生在断索后约1.34s，拱肋最大位移为4.78mm，发生在断索后约1.93s；纵梁位移与拱肋位移的比值为1.49。

由上述分析可知，网格结构吊索在发生吊索断裂后，在冲击作用下纵梁吊点的位移小于平行吊索拱桥发生吊索断裂时纵梁吊点的位移，并且纵梁位移与拱肋位移的比值也小于平行吊索拱桥，因此网格结构吊索拱桥在发生吊索断裂时，对纵梁与拱肋的影响程度比小于平行吊索拱桥，即平行吊索对纵梁影响程度更大，而网格吊索对纵梁影响程度小。

图7 2#纵梁吊点与3#拱肋吊点位移时程曲线

3.2.2 吊索

对于网格结构吊索的跨径85m下承式刚架系杆拱桥，在次短吊索断裂时的冲击荷载作用下，断裂吊索相邻3#吊索处于最不利的受力状态。图8给出了断裂短吊索相邻的吊索的轴力时程曲线。可以看出，3#吊索初始轴力为937.07kN，在断索冲击作用下轴力最大值1331.82kN，发生在吊索断裂后约1.410s。轴力变化比为42.13%，大于平行吊索的36.6%。

图8 2#纵梁吊点处另一吊索轴力时程曲线

3.2.3 纵梁

在次短吊索断裂时的冲击荷载作用下，吊索断裂处纵梁截面(2#)处于最不利的受力状态。图9给出了吊索断裂处纵梁截面(2#)的应力时程曲线。可以看出，吊索断裂处纵梁截面(2#)的初始应力为4.071MPa，在断索冲击作用下应力最大值为6.386MPa，发生在吊索断裂后约1.405s。应力变化比为56.9%，小于平行吊索的112.5%。

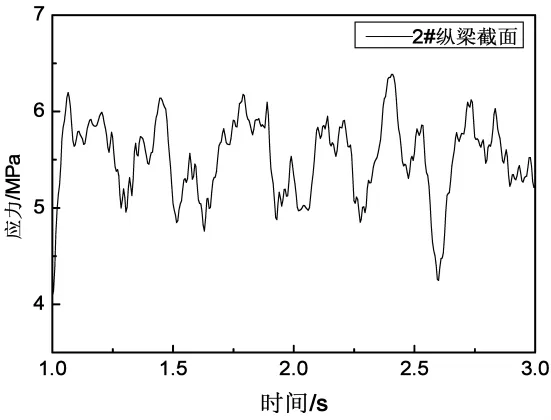
图9 2#纵梁截面应力时程曲线

由上述分析可得，设有网格状吊索的拱桥相较于平行吊索拱桥而言，由于吊索数量增加，因此初始索力较小，断索后断裂吊索所在的拱肋吊点与纵梁吊点位移也较小，在最不利位置出现的吊索轴力极大值与纵梁应力也较小。并且网格结构吊索在发生吊索断裂时，对拱肋与桥面系的影响分化程度也不如平行吊索拱桥。由于网格状吊索在同一纵梁吊点处有两根不同的吊索，因此当一根吊索断裂时，另一根将会对纵梁起到限制位移的作用，该吊索同时受到纵梁的冲击拉伸作用，因此会出现吊索轴力变化比大于平行吊索拱桥，而纵梁应力变化比小于平行吊索拱桥的情况。吊索断裂造成桥面系垮塌的主要原因在于桥面系的受力情况与抗力大小，网状结构吊索断裂后，对纵梁的受力变化不如平行吊索拱桥，因此网状拱桥结构的桥面系强健性大于平行吊索拱桥。

4 结论

(1)网格结构吊索断裂后，桥面系位移大于拱肋位移，因此网格吊索断裂对桥面系的影响大于拱肋。

(2)与平行吊索结构相比，网格吊索对桥面系与拱肋的影响分化程度较小，即平行结构吊索断裂对桥面系更不利。

(3)网状结构吊索断裂后，对纵梁的受力变化不如平行吊索拱桥，因此网状拱桥结构的桥面系强健性大于平行吊索拱桥。