基于带外生变量自回归模型的福建省交通工程材料价格预测研究

■丘永宜

(福建省交通工程造价管理站，福州 350001)

0 引言

交通工程建设过程中工程造价管理贯穿于项目始终，材料费属于建筑安装工程费中的重要组成部分，通常占整个工程项目造价的55%～70%比重，而构成建筑主体的主要材料的材料费占总造价比重往往可以达到50%～60%左右。交通工程项目建设具有周期长的特点，期间工程材料的价格波动对工程建设成本有着重大的影响，施工周期中价格变化难以有效确定，尤其是施工期间和投标期间的价格也可能存在较大的变化。然而，当前造价主管部门制定的指导价价格也主要以每月月底的市场调查统计结果进行整理并发布，其价格数据均存在一定的滞后性，因此探索形成定量化的价格预测模型，进而准确把握建筑材料市场价格的动态变化则成为接下来项目工程造价管控的重要方向。

陈可嘉等运用灰色关联分析法对影响交通工程材料价格的重要影响因素进行了关联度分析并排序，在一定程度上研究确定了各影响因素的量化重要程度，为建设项目各参与方更好的掌握材料价格的变化趋势提供了依据[2]。井霞霞等在其文献中采用考虑外生变量的基于分数差分的预测模型对石油价格进行线性自回归研究，通过模型得到了比较准确的石油预期价格[3]。Antonio在研究中短期内专利申请商标注册的发展趋势时使用了带有外生变量的时间序列模型，通过对比其他方法，发现考虑以GDP、工业生产指数等作为外生变量带入时间序列模型中能大大提高预期结果的准确度[4]。本文提出将影响价格变动的重要影响因素作为外生变量与材料价格自回归预测模型相结合的方法，用于福建省交通工程材料价格预测的实证研究当中。

1 带外生变量的自回归模型

1.1 模型介绍

(1)自回归模型AR(p)

自回归模型[1](AutoregressiveModel)是用自身做回归变量的过程，即利用前期若干时刻的随机变量的线性组合来描述以后某时刻随机变量的线性回归模型，它是时间序列中的一种常见形式。P阶自回归模型记作AR(p)，满足下面的方程：

式中 c 为常数；φ1，φ2.....φp是自回归模型系数；p 为自回归模型阶数；εt是均值为0的扰动项，方差σ2为白噪声序列。对于任意 s＜t，有 E(xsεt)=0，即意味着当前扰动项的值与过去的时间序列值无关。

(2)带外生变量的自回归模型

通常情况下数据具有自我记忆性，但是也受到外部因素的影响，具有外生变量的自回归模型将往期数据和外生变量同时引入自回归模型中进行回归分析，基本模型方程形式见公式2：

其中yt、zt为代表影响因素的外生变量。

1.2 福建省交通工程材料价格预测定价模型的构建

基于带外生变量的自回归模型的福建省交通工程材料价格预测定价模型的构建具体包括以下几个步骤：

(1)影响因素分析及外生变量的选取

根据相关文献以及实际工作角度，选择对交通工程材料价格存在潜在影响的相关因素作为外生变量的初步选择项。主要考虑从交通工程材料的整体影响因素结合需要分析研究的材料本身属性进行分析和选取，例如带肋钢筋属于钢材的一类，钢材价格的影响因素也直接对带肋钢筋价格产生影响。外生变量数据的获取必须考虑材料的共性影响因素结合自身的特性进行分析，涉及影响因素指标各有不同，一般包括国内宏观经济、材料成本、进出口量，国际市场环境指标等。关于材料价格影响因素指标的数据搜集主要从国家统计局网站、美国能源情报署官方网及前瞻网数据库等获得。

(2)历史指导价数据的平稳性检验

通过对所要研究数据序列本身的平稳性进行检验，来判断数据序列能否使用自回归模型，只有通过平稳性分析的材料价格序列才能进行下一步的自回归分析。本文形成的自回归预测模型，对所要研究的交通工程材料历史指导价数据的时间序列采用ADF检验方法。

ADF检验(AugmentedDickey-FullerTest)方法通过在回归方程右边加入拟选用时间段的材料价格数据作为因变量yt的滞后差分项来控制高阶序列相关，包括3种形式的回归模型：

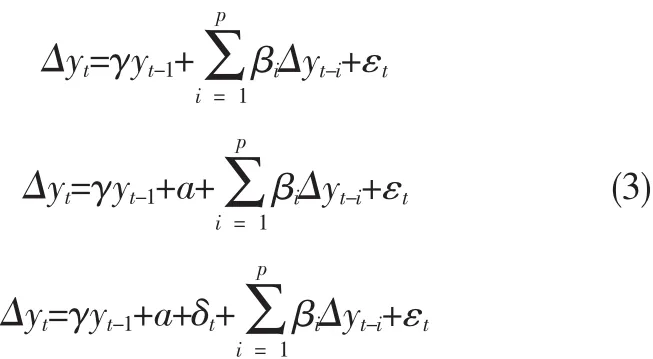
原假设 H0：γ=0，备选假设为 HI：γ＜0，即原假设为：序列存在一个单位根；备选假设为：不存在单位根，序列可能还包含常数项和时间趋势项。通过比较γ的估计值γˆ的t统计量与设定的1%、5%和10%显著性水平下t统计量的临界值，从而判断是接受原假设，还是拒绝原假设、接受备选假设。只有将材料价格时间序列带入假设中所对应的1%、5%、10%临界值，在1%、5%、10%的水平下拒绝原时间序列存在单位根的原假设，该材料价格序列才通过了平稳时间序列。

(3)历史指导价数据自相关性检验与模型阶数的确定

进行序列自相关性检验的方法有：自相关系数AC及偏自相关系数PAC和Ljung-BoxQ统计量。自相关系数可以部分地刻画一个随机过程的性质，其在于表明时间序列{μt}的邻近数据之间是否存在相关性；偏自相关系数是指在给定 μt-1，μt-2，......，μt-k-1的条件下，μt与 μt-k之间的条件相关性。通过时间序列的自相关图，可以直观地判断自相关系数与偏自相关系数的拖尾或截尾特征，以及相关系数是否显著异于0，若相关系数显著异于0则表明序列存在自相关性。而Q统计量在某一滞后阶数显著不为零大于显著水平下的临界值，且伴随概率值小于显著水平时，可说明该时间序列存在某种程度上的自相关性。

将材料价格的时间序列设为Xt、Xt-1……Xt-p，对于自相关性检验方法，本文提出通过自相关图，根据AR模型识别的自相关性函数和偏相关函数的特性进行检验并确定阶数：

1)平稳材料价格序列的AR(p)模型有两个显著的性质：一是拖尾性，即自相关系数ρk始终存在着非零的取值，当k大于某一常数之后其就恒等于0的情况不会出现；二是自相关函数呈正弦振荡形式衰减或指数衰减。自相关函数公式：

2)由材料时间序列构成的平稳AR(p)模型偏自相关函数(见公式5)具有p步截尾的特性。当k≤p时，，φkk≠0;当k＞p时，φkk=0。实际使用中，对带入材料价格的阶数判断，利用偏自相关函数的截尾性特性，通过软件形成自相关图，来识别AR(p)模型的阶数。

(4)材料价格影响因素带入自回归模型并进行显著性检验

将相关影响因素作为外生变量带入已完成阶数识别的AR(p)模型中，构建带外生变量的自回归模型(公式2)，对变量重复进行显著性检验，未能通过显著性检验的从模型中剔除，直到变量均通过显著性检验，此时根据最终得到方程即为该种材料预期指导价定价模型公式。

(5)形成定价模型的应用评价

根据以上方法形成的材料价格预测模型的精度可以根据该模型计算出的预测价格(预期值)，取数期(通常取三期)进行计算检验，通过将得到预测价格与实际价格差值的绝对值与实际价格的比值大小来对模型精度进行衡量和分析，评价模型的准确度检验公式：

式中：x′为预测价格；x为实际指导价价格。

2 实证研究

本节利用E-Views软件作为建模工具，分别以水泥(42.5级)、钢筋(带肋)和石油沥青(进口)为例作为具有代表性的交通工程主材，选取福建省交通工程材料价格信息数据库中时间跨度为2008年1月至2017年12月的福州市历史指导价数据组成时间序列进行模型应用分析，每一个变量共120个观测值，考虑价格波动的自我记忆性，通过采用自回归模型将往期材料指导价价格和外生影响因素进行共同考量，得到各主材的预测价格计算式。

2.1 水泥价格预测定价模型

(1)影响因素分析及外生变量的选取

水泥作为“建筑工业的粮食”也是交通工程的基本材料之一，使用量大、投资成本占比高。而影响水泥价格的因素很多，归纳起来主要有四个方面的影响因素：宏观经济、供求关系、汇率影响、生产成本[2]。本文将美元对人民币汇率指数、水泥销量、水泥产量、居民消费价格指数、国内生产总值、固定资产投资、煤炭产量7种作为相关影响因素纳入到对水泥价格预测的定价模型中。

(2)水泥价格时间序列的平稳性检验

水泥主要分为32.5级水泥和42.5级水泥两种类型，考虑到研究方法上的一致性，本节仅选择一种水泥类型来进行分析。选取2008年1月至2017年12月42.5级水泥价格、美元对人民币汇率指数、水泥销量、水泥产量、居民消费价格指数、国内生产总值、固定资产投资、煤炭产量的月度数据为研究对象，将研究所涉及到的8组时间序列分别记为：{Yt}、{αt}、{βt}、{χt}、{δt}、{ηt}、{φt}、{γt}。

对于42.5级水泥的价格序列 {Yt}，经单位根检验(ADF检验)(表1)可知ADF检验值均小于所对应的1%、5%、10%的临界值，因此在1%、5%、10%的水平下拒绝原时间序列存在单位根的原假设，得{Yt}为平稳时间序列。

表1 42.5级水泥价格序列{Yt}的ADF检验结果

(3)42.5级水泥价格序列自相关性检验与模型阶数的确定

对于由带肋钢筋历史指导价数据构成的时间序列，进行自相关系数AC及偏自相关系数PAC和Ljung-BoxQ统计量检验，通过软件计算可得序列{Yt}的相关图(见图1)：

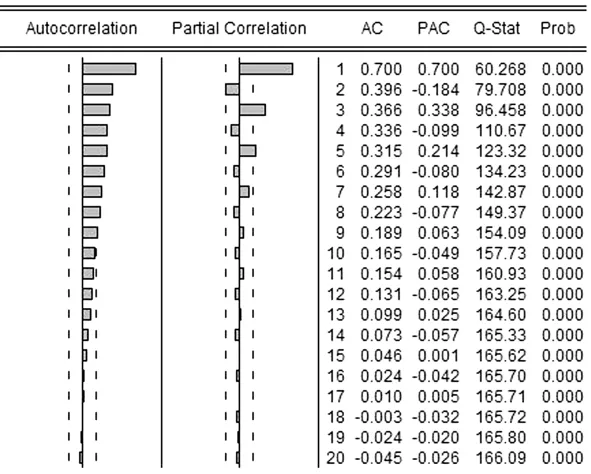
图142 .5级水泥价格序列{Yt}的相关图

从图1可以看出序列{Yt}的自相关系数是拖尾的，偏自相关系数在3阶截尾，42.5级水泥价格序列满足AR(3)的过程。

(4)外生变量带入自回归模型并进行显著性检验

为更准确地对42.5级水泥价格进行预测，将美元对人民币汇率指数序列{αt}、水泥产量序列{βt}、水泥销量序列{χt}、居民消费价格指数序列{δt}、国内生产总值序列{ηt}、固定资产投资额序列{φt}以及煤炭产量序列{γt}作为外生变量带入到自回归预测模型中，得到回归估计结果如表2所示。

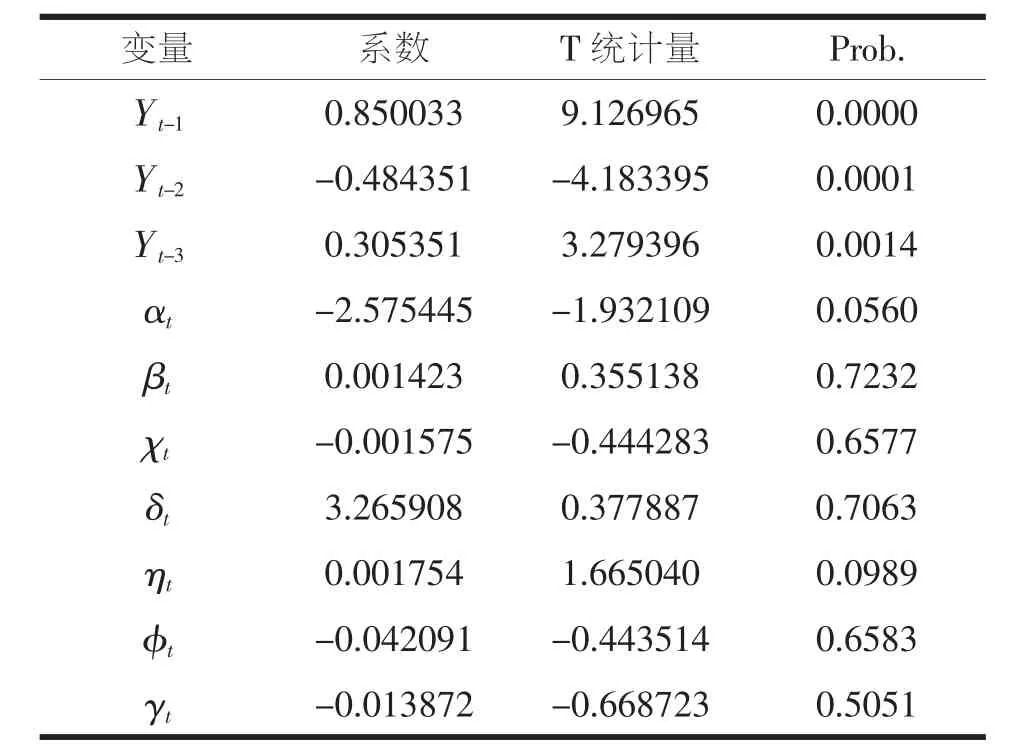
表2 考虑外生变量的自回归定价模型估计结果

通过表 2 可知：变量 βt、 χt、 δt、 φt、 γt未能通过 10%的显著性检验，因此将它们从模型中剔除，仅保留其他通过显著性检验的变量，将保留的变量再次带入自回归模型可得模型估计结果，如表3：

表3 考虑通过显著性检验的外生变量的自回归定价模型估计结果

通过表3可知，所有保留变量均通过显著性检验，εt为扰动项，故可得42.5级水泥价格预测的计算式如下：

该定价公式，从下图2显示的回归方程的残差序列的自相关系数和偏自相关系数可以看到不存在序列相关，说明模型可以较好地拟合序列{Yt}。

图2 序列{Yt}方程残差序列的相关图

2.2 钢筋价格预测定价模型

带肋钢筋属于钢材的一类，钢材价格的影响因素也直接会对带肋钢筋价格产生影响。相关影响因素可以总体分为三大类：宏观经济、生产成本和国际市场的影响。

选取的主要影响因素为：固定资产投资额、居民消费水平支出、国内生产总值、焦炭产量、粗钢产量、铁矿石产量、高炉生铁产量、国际钢铁价格指数等8种[2]。结合2008年1月至2017年12月间带肋钢筋的价格，时间序列分别记为：{Yt}、{αt}、{βt}、{χt}、{δt}、{ηt}、{φt}、{γt}、{ρt}。 通过模型计算检验步骤，得到带肋钢筋价格预测的计算式：

2.3 石油沥青价格预测定价模型

石油沥青是原油加工过程的附属产品，在工程建设项目上主要作为高速公路、大型水利工程和大型建筑工程的路面和防水项目中的基础建设材料，在交通运输(道路、铁路、航空等)工程项目投资成本占比巨大。

选取的主要影响因素为：美元对人民币汇率、美元指数、美国商品研究局指数(CRB指数)、世界原油库存量以及世界石油产量等5种[2]，结合2008年1月至2017年12月间进口石油沥青的价格，时间序列分别记为：{Yt}、{αt}、{βt}、{χt}、{δt}、{ηt}。 通过模型计算检验步骤，得到进口石油沥青价格预测的计算式：

2.4 价格预测定价模型的评价

根据上述模型计算出2018年1月到3月42.5级水泥、带肋钢筋和进口石油沥青的预测价格，并将其与实际值进行比较(公式6)，以评估价格预测定价模型的精度。

表4 根据预测定价模型计算的预测价格与实际价格的比较

从表4可以看到，就短期预测价格的精度而言均在10%以内，考虑到2008年以来交通工程材料价格所表现出的较大的波动性，本文结合影响因素分析所得的价格预测定价模型计算的价格具有较好的预期把握能力。其中，模型对于带肋钢筋价格的预测精度较高，均控制在3%以内。

3 结语

在实际应用当中，通过模型进行价格预测可以从纵向的维度对当期交通工程材料指导价的制定进行考量，起到与传统的定价方法互相弥补和支撑的作用。较为准确有效的价格预测机制有助于把握市场涨跌幅度的预期，使交通工程材料指导价在制定过程中得到有效修正。