基于混合裁剪失衡数据增强与SwinNet网络的滚动轴承故障诊断

火久元, 李宇峰, 常 琛, 李超杰, 许继豪

(1. 兰州交通大学 电子与信息工程学院,兰州 730070;2. 兰州瑞智元信息技术有限责任公司,兰州 730070)

目前,故障诊断技术已逐渐成为提升机械系统可靠性和安全性的关键手段[1]。优秀的故障诊断方法可以准确判断故障发生的位置,辨识发生故障的类型,避免造成严重的经济损失和人身伤害[2]。滚动轴承作为旋转机械系统关键部件之一,在各个行业中都有非常广泛的应用[3],是影响机械设备能否安全运行的重要因素[4]。因此,开展滚动轴承故障诊断研究对提高机械设备运行效率,实现机械设备健康管理具有重要意义。

对滚动轴承进行故障诊断的方法通常分为4类,分别是基于模型的、基于经验的、基于传统机器学习的与基于深度学习的[5]。但是由于现代工业设备比较复杂并且缺乏足量的先验知识,因此通过基于模型的或者基于经验的故障诊断方法存在一些限制条件[6]。传统的机器学习方法已经被广泛的应用于故障诊断领域。Van 等[7]使用经验模态分解对信号进行分解,然后利用支持向量机算法来对轴承故障进行分类,取得了显著的分类效果,但其需要手动进行特征提取与特征选择,存在一定的局限性。He等[8]提出了一种利用多尺度随机共振谱图来对轴承进行故障制度的方法,但是此方法在处理大量振动信号时计算难度大,且过度依赖于研究人员的专业知识。

近年来,深度学习方法由于其具有自适应地从监测数据中进行故障特征学习的优势,得到越来越广泛的关注。如吴春志等[9]设计出了一种一维卷积神经网络,以原始振动信号作为模型输入完成了对齿轮箱的故障诊断。张立智等[10]提出了一种利用短时傅里叶变换结合卷积神经网络模型进行故障诊断的方法,该模型具有强大的特征提取能力。Han等[11]提出了一种将卷积神经网络的特征处理能力与支持向量机的泛化能力相结合的方法,解决了小样本数据集难以训练复杂模型的问题。此外,一些学者在故障诊断模型中引入了注意力机制来增强卷积神经网络处理长距离依赖关系等方面的能力。Li等[12]引入了一种注意力机制来辅助单位信息数据段,提取输入的判别特征来完成滚动轴承的故障诊断。Ding等[13]构建了一种拥有全新的注意力机制的TransFormer结构,实现了滚动轴承端到端的故障诊断。

在理想的环境中,各种故障诊断方法都能够取得出色的效果,尤其是在大量故障样本和健康样本进行训练的情况下对滚动轴承进行故障诊断。这样的训练数据确保了算法具备足够的准确性。如果在没有环境噪声和人为噪声干扰的情况下,这些方法甚至可以实现接近100%的故障诊断精度。然而,机械设备通常处于正常服役状态,其故障样本数量往往远少于正常样本数量[14]。此外,大多数滚动轴承密闭于机械系统内部,受到电磁干扰的影响会让采集到的振动信号中不可避免地包含噪声[15]。同时,在对故障数据进行标记时可能会出现人为的操作失误而导致真实标签与标记标签不符的情况发生[16]。这些情况的出现都会大幅度降低故障诊断模型的诊断精度。因此,本文提出了一种基于混合裁剪失衡数据增强与SwinNet网络相结合的故障诊断模型,利用混合裁剪失衡数据增强算法来解决故障类别失衡问题,同时有效地结合SwinNet网络,完成在有噪声干扰与在有噪声标签干扰时对滚动轴承的故障诊断。

1 理论基础

1.1 小波变换

相较于一维信号,二维图像是更强大的信息表达方式。小波变换是一种信号处理技术,它能够将信号分解为不同尺度和频率成分。在低频段,小波变换能够提供更高的频率分辨率和更低的时间分辨率,在高频段,小波变换能够提供更高的时间分辨率和更低的频率分辨率,这与信号变换的特性相符[17]。因此,本文使用小波变换来将滚动轴承振动信号转换为二维时频图像,从而能够同时显示全局的低频信息和局部的高频特征,更好地揭示故障信号的本质特征[18]。小波变换操作如式(1)所示

(1)

式中:a为尺度参数,a>0;b为时间平移量;P(b)为原始的故障信号;φ为母小波;Wp(a,b)为连续小波变换。

1.2 卷积神经网络

卷积神经网络(convolutional neural networks, CNN)是一种常见的深度学习神经网络模型,常用于图像和视频等数据的分类和处理。CNN的基本结构大多由卷积层、池化层和全连接层组成。

卷积层是CNN中最重要的层级之一,它的主要目的是从输入数据中提取特征[19]。一般的卷积计算如式(2)所示

Mi+1=[Mi⊗Wi]+d

(2)

式中:Mi+1为第i层的特征输出图;Mi为第i层的特征张量;Wi为第i层感受器的权值向量;d为第i层的偏置向量; ⊗为卷积计算。

池化层是一种常用的降采样技术,用于减少卷积层输出的特征图的大小[20]。主要池化操作有最大池化和平均池化,如式(3)、式(4)所示

(3)

(4)

式中:uP(i,t)为第p层中第i个特征张量的第t个神经元;w为卷积核宽度;j为第j个池化层。

全连接层是将前面的卷积层和池化层的输出连接成一个全连接的神经网络层,用于对输入特征进行分类或者回归。如式(5)所示

q(x)=f(wx+c)

(5)

式中:x为全连接层的输入;w为权重;c为偏置;f为激活函数。

1.3 Transformer

随着Transformer模型在自然语言处理领域的成功应用,研究人员开始将其引入到了图像处理领域。最早的工作是将Transformer应用于图像分类任务中,这些模型通常被称为ViT(vision transformer)[21]。ViT将图像的像素数据视为一维序列,通过将像素转换为一组向量后送入到对应模块中进行分类。为解决ViT在处理图像时需要大量的计算和内存资源的问题,提出了一种Swin Transformer网络作为可行解决方案,其拥有类似于金字塔形式的架构,可以大大降低模型对于计算和内存的要求[22]。传统的Swin Transformer块结构如图1所示。

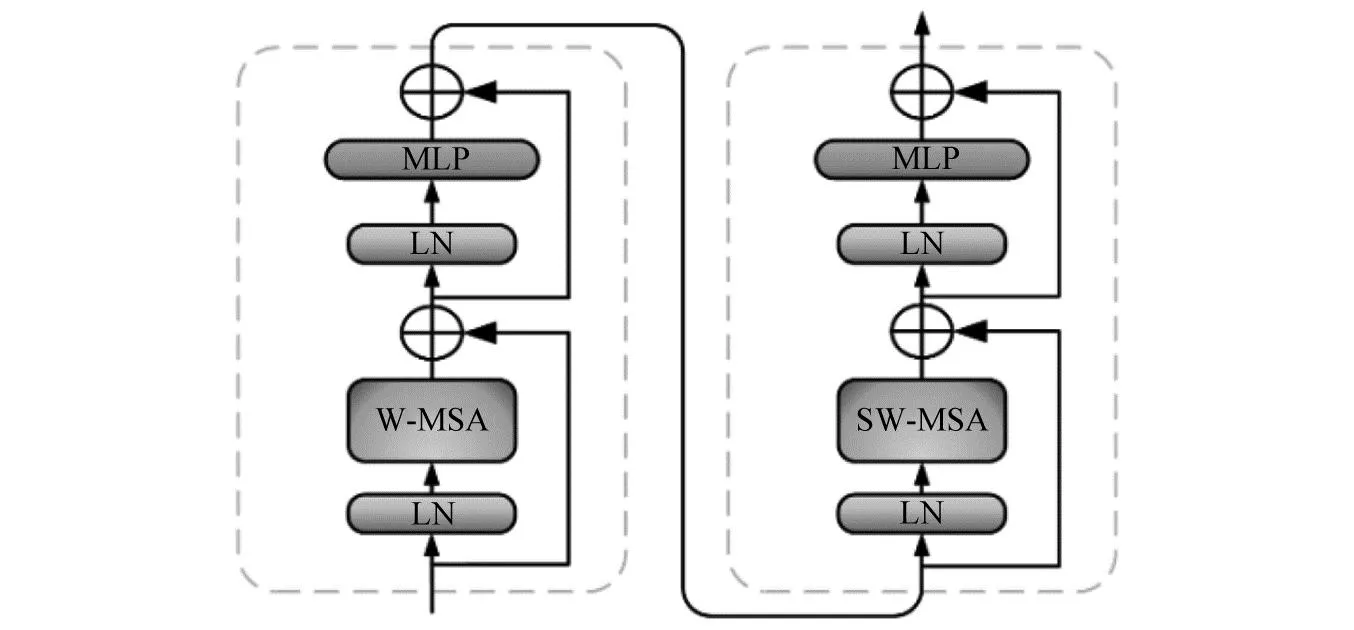
图1 Swin Transformer块结构Fig.1 Swin Transformer block structure

图1中,Swin Transformer采用了一种窗口化的自注意力机制,将输入的特征图分割成多个大小相同的窗口,每个窗口内部进行多头注意力机制的计算。通过这种方式,模型可以仅对每个窗口内的信息进行关注和计算,避免了对整个图像的计算。此外,为了使信息在窗口之间进行传递,Swin Transformer还采用了一种移动窗口的自注意力运算机制,该机制可以将注意力权重向左或向右偏移一定距离,以实现窗口间的信息交流。

2 基于混合裁剪失衡数据增强与SwinNet网络的故障诊断模型

2.1 混合裁剪失衡数据增强算法

在实际工况下,正常样本数量通常远远多于故障样本数量,这往往会导致故障诊断模型诊断能力降低以及泛化能力不够等问题。受到Bai等[23]提出的数据增强算法启发,通过借鉴图像裁剪的数据增强思想,本文提出了一种混合裁剪失衡数据增强(mixed-cutout imbalanced data augmentation,MCIDA)算法,如式(6)所示

(6)

式中:S为通过一次MCIDA算法进行扩充后的样本数;M为数据集原始时间序列长度;N为数据样本长度;K为需要对原始数据集进行扩充的倍数;i的取值为1～K的整数。

当数据失衡的情况发生时,为生成足够多的数据来作为故障诊断模型的输入,对于失衡的故障数据类别通过MCIDA算法进行样本扩充,保证扩充后的故障类别样本数尽量与滚动轴承健康状况下的样本数相同。以对失衡的故障类别进行5倍混合裁剪失衡数据增强为例,其原理如图2所示,对应的算法原理伪代码如表1所示。

表1 算法原理伪代码Tab.1 Pseudocode for algorithm principle

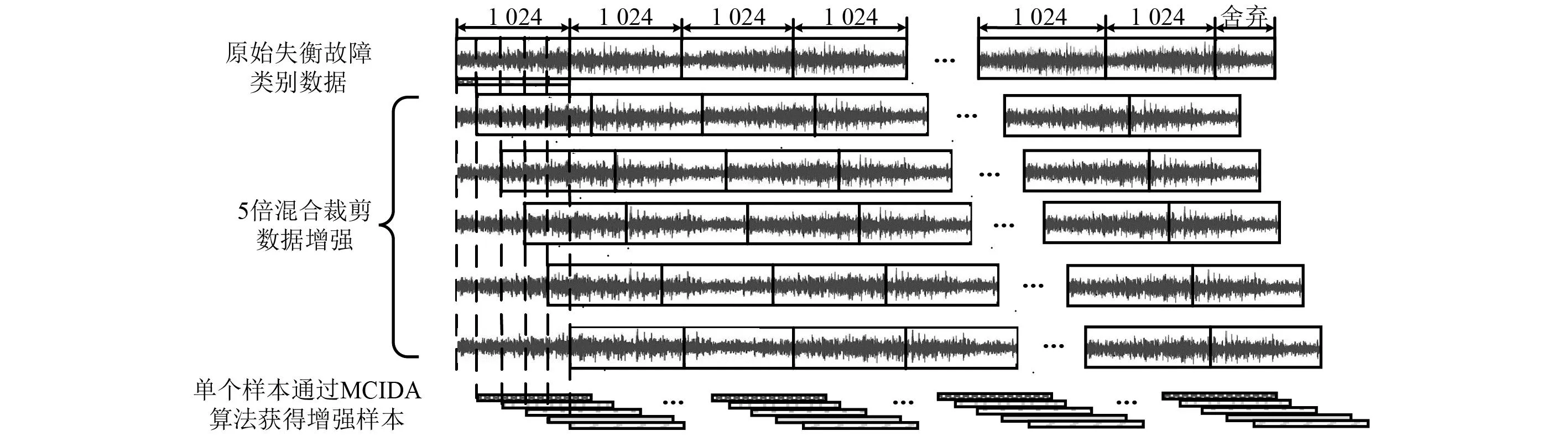
图2 5倍混合裁剪失衡数据增强Fig.2 5 times mixed cropping imbalanced data augmentation

结合图2与见表1,原始数据集的失衡类别样本按照该算法最终可以获得5组样本集,将这5组样本集进行混合就可以获得最后的增强数据集。

通过MCIDA算法进行重新划分获得的样本集中的各个样本一定不会发生重复,并且增强数据集中的任何一个样本也不会与原始数据集失衡类别中的样本相同。

2.2 SwinNet网络

滚动轴承的故障特征受到振动耦合的影响往往会表现出多尺度性质[24]。基于传统CNN的故障特征提取方法已无法适用于较为复杂的滚动轴承故障诊断场景中,为提高故障诊断模型的性能,需要获取更加全面的故障特征,因此,本文将CNN与Swin Transformer编码器相结合设计出了以时频图像作为输入的SwinNet网络模型。该SwinNet网络结构如图3所示。

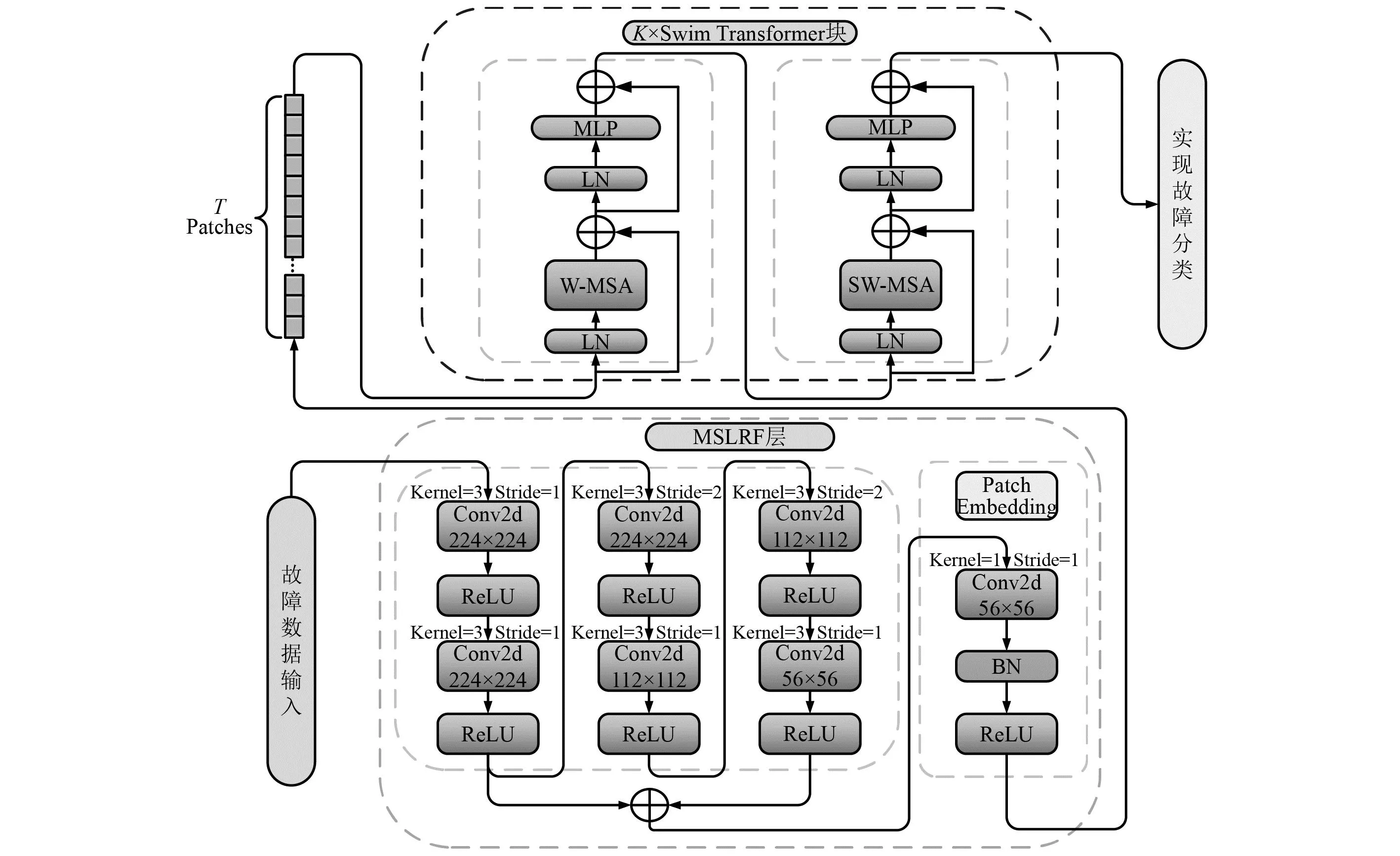
图3 SwinNet网络模型结构Fig.3 SwinNet network model architecture

该网络包含了一个多尺度局部感受野特征提取(multi-scale local receptive field feature extraction,MSLRF)层和多个Swin Transformer编码器。首先,借助卷积核的带通滤波特性,利用MSLRF 层中的卷积模块提取图像的低维特征,保证每个卷积层可以捕获不同尺度和方向的局部信息。然后,利用MSLRF层中的Patch Embedding能力将每一张图片分解为多个小块,从而更好地表示图像中的局部信息。最后,将提取到的每个小块中的局部窗口特征传递到Swin Transformer编码器中实现跨窗口交互捕捉全局信息,从而进一步提高特征提取能力。总之,SwinNet网络可以将CNN的归纳偏置能力与Swin Transformer编码器的移动窗口多头注意力机制进行结合从而完成滚动轴承故障的高效诊断。

2.3 故障诊断流程

基于MCIDA-SwinNet方法的故障诊断整体流程如图4所示。具体过程如下:

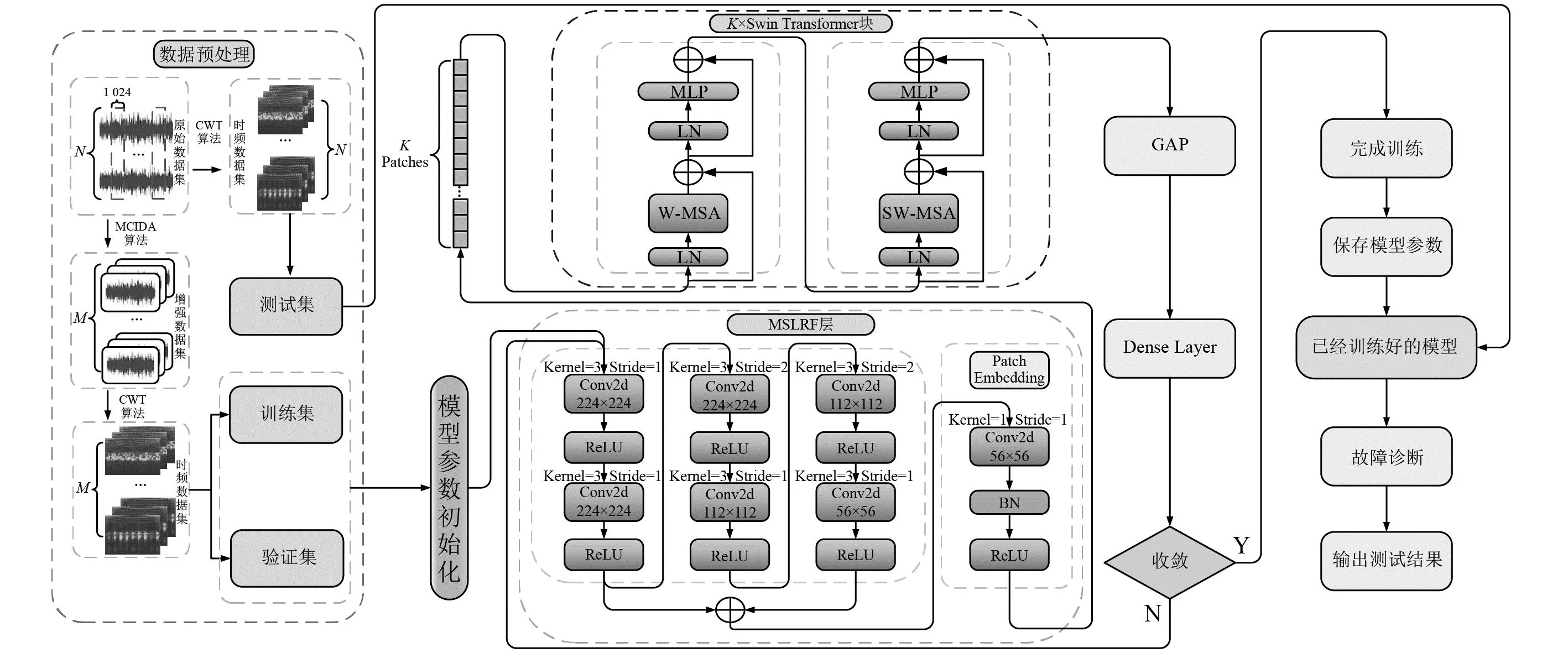
图4 基于MCIDA-SwinNet方法的故障诊断流程Fig.4 Thefault diagnosis process based on MCIDA-SwinNet method

(1) 对原始的振动信号数据进行样本的划分,将需要进行数据增强的失衡数据集按照MCIDA算法进行数据增强。通过小波变换算法对增强数据集与原始数据集进行时频图像的转换,并且将增强数据集按照比例划分为训练集与验证集,原始数据集作为测试集。

(2) 对SwinNet网络的参数进行初始化,设置SwinNet网络的drop_rate参数为0.1,droppath参数为0.2,使模型在训练过程中随机丢弃网络中的某些连接,减少不同层之间的耦合和复杂性,从而增加模型的鲁棒性和泛化能力,防止过拟合的产生。此外,设置SGD(stochastic gradient descent)优化算法来更新网络超参数,将学习率初始化为0.001,根据验证集的损失函数值动态更新学习率,并且设置权重衰减参数进一步减小过拟合的风险。

(3) 网络进行训练,首先,输入数据经过MSLRF层和多个Swin Transformer块得到表示图像信息的特征向量。然后,特征向量输入到全局池化层中得到完整的图像语义表示。最后,通过全连接层进行故障分类。当验证集的损失函数值不再下降时,保存收敛后的模型。将测试集输入到训练好的模型之中,最终得到故障诊断分类结果,完成故障诊断流程。

3 试验验证与分析

为验证所提出的故障诊断方法的诊断性能,本文使用美国凯斯西储大学(Case Western Reserve University,CWRU)电击轴承采集的公开数据集进行试验。采用的深度学习框架为Pytorch,在Windows Server 2016上利用python语言进行编程。计算机的配置为:Inter(R) Xeon(R) Silver 4210R CPU @ 2.40 GHz 2.39 GHz,NVIDIA Tesla T4显卡,64 GB内存。为客观反映试验的有效性并且排除偶然性,每组试验都重复多次,然后取平均值作为最终结果。

3.1 数据说明

本试验进行诊断的轴承型号为SKF6205[25],该轴承存在3种故障损伤的位置,分别是轴承滚动体故障、外圈故障与内圈故障。3种故障损伤的损伤直径大小分别为0.177 8 mm、0.355 6 mm、0.533 4 mm。每一种故障数据可以分别通过驱动端、风扇端、底座端的加速度计来收集到。本文所使用的故障数据是当电机转速为1 772 r/min,采样频率为12 kHz时,从驱动端的传感器获得的轴承振动信号数据。按照该轴承故障位置与故障直径进行轴承状态类别划分,其状态类别可以划分为10类。将该轴承振动信号数据以1 024个样本点为1个样本进行样本划分,得到不同状态类别的时域波形图像与频域波形图像如图5所示。

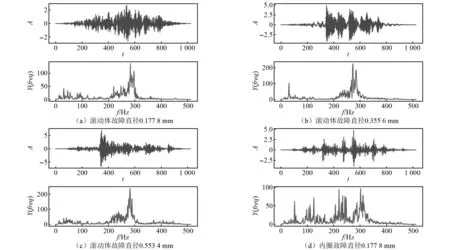
图5 不同状态类别的时域波形图与频域波形图Fig.5 Time-domain waveform and frequency-domain waveform images of different state categories

3.2 基于MCIDA算法的数据增强试验

本试验依据滚动轴承不同状态类别的失衡样本数量的失衡比值(imbalance ratio,IR)构造了4组失衡数据集。其失衡样本数量的比值如式(7)所示。

IR=X∶Y

(7)

式中:X为故障样本的数量;Y为健康样本的数量。IR分别设置为1∶20、1∶10、1∶5、1∶2,4组失衡数据集的9种故障状态与1种健康状态的样本数量如表2所示。设置每组失衡数据集的健康样本数量为200个,故障类别样本数量分别设置为10、20、40、100个。得到划分后的4组失衡数据集的样本总数分别为290、380、560、1 100个。

基于MCIDA算法来构造增强数据集,对第1组失衡数据集进行增强,每一类的失衡故障样本数将由10个扩增到180个。同样的使用该MCIDA算法可以分别将第2、3、4组的失衡故障样本数扩充到190、195和198个。这样最后获得的4组增强数据集的样本总数分别为1 820、1 910、1 955、1 982个。自此一共得到8组数据集,即4组原始失衡数据集与4组增强数据集。

使用小波变换算法将8组数据集的振动信号数据样本转换为二维时频图像数据样本,以此图像数据作为SwinNet网络的输入数据。考虑到较小尺寸时频图像信号的某些部分会纠缠到一起导致无法区分,而根据奈奎斯特-香农采样定理,适当的增加图像尺寸可以改善这一问题[26]。综合考虑使用尺寸为224×224的时频图像作为网络模型的输入数据。该滚动轴承10种不同状态类别下的二维时频图像,如图6所示。由图6(a)～图6(c)可知,不同直径的滚动体故障呈现出周期性的、分离的特征,其周期性特征与故障直径相关; 由图6(d)～图6(f)可知,不同直径的内圈故障在特定频率上展现出独特的时域反射特征强度;而由图6(g)～图6(i)可知,不同直径的外圈故障在不同频率和时域上会表现出短时能量集中的特征;只有图6(j)所展示的健康轴承状态的二维时频图像呈现出了均匀且较为平滑的特征。

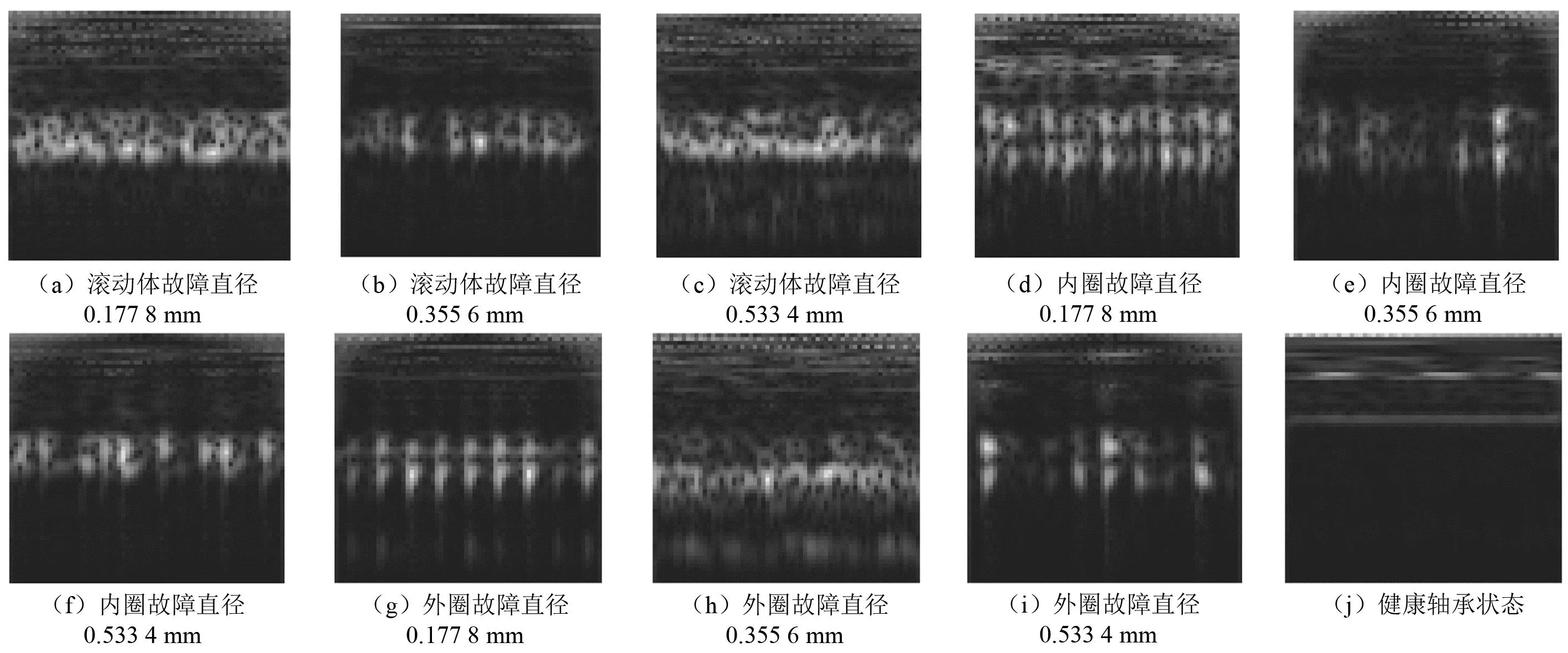
图6 二维时频图像Fig.6 Two dimensional time-frequency images

使用失衡数据集按照7∶3的比例划分出训练集和验证集进行SwinNet网络训练的训练情况如图7(a)所示,unba_10、unba_20、unba_40、unba_100分别代表的是使用4组失衡数据集进行训练的曲线。由于失衡数据集故障样本较少,正常样本较多,这导致网络训练曲线波动性较大,稳定性不够。随着类失衡程度加剧,SwinNet网络的特征提取能力减弱,其在IR为1∶20时的训练精度只能达到94.12%左右。为了验证MCIDA算法不仅能够提高网络训练的稳定性,还可以提高网络的特征提取能力,针对每一组增强数据集按照7∶3的比例划分出训练集和验证集,而将原始的失衡数据集作为测试集。SwinNet网络使用增强数据集训练的情况如图7(b)所示,ba_10、ba_20、ba_40、ba_100分别代表的是使用4组增强数据集进行训练的曲线。可以发现使用增强数据集进行训练的曲线波动非常小,具有较强的稳定性,当迭代到第50次后,所有的训练曲线都达到收敛状态。最后4组增强数据集的训练集平均收敛精度都可以达到98.7%左右。

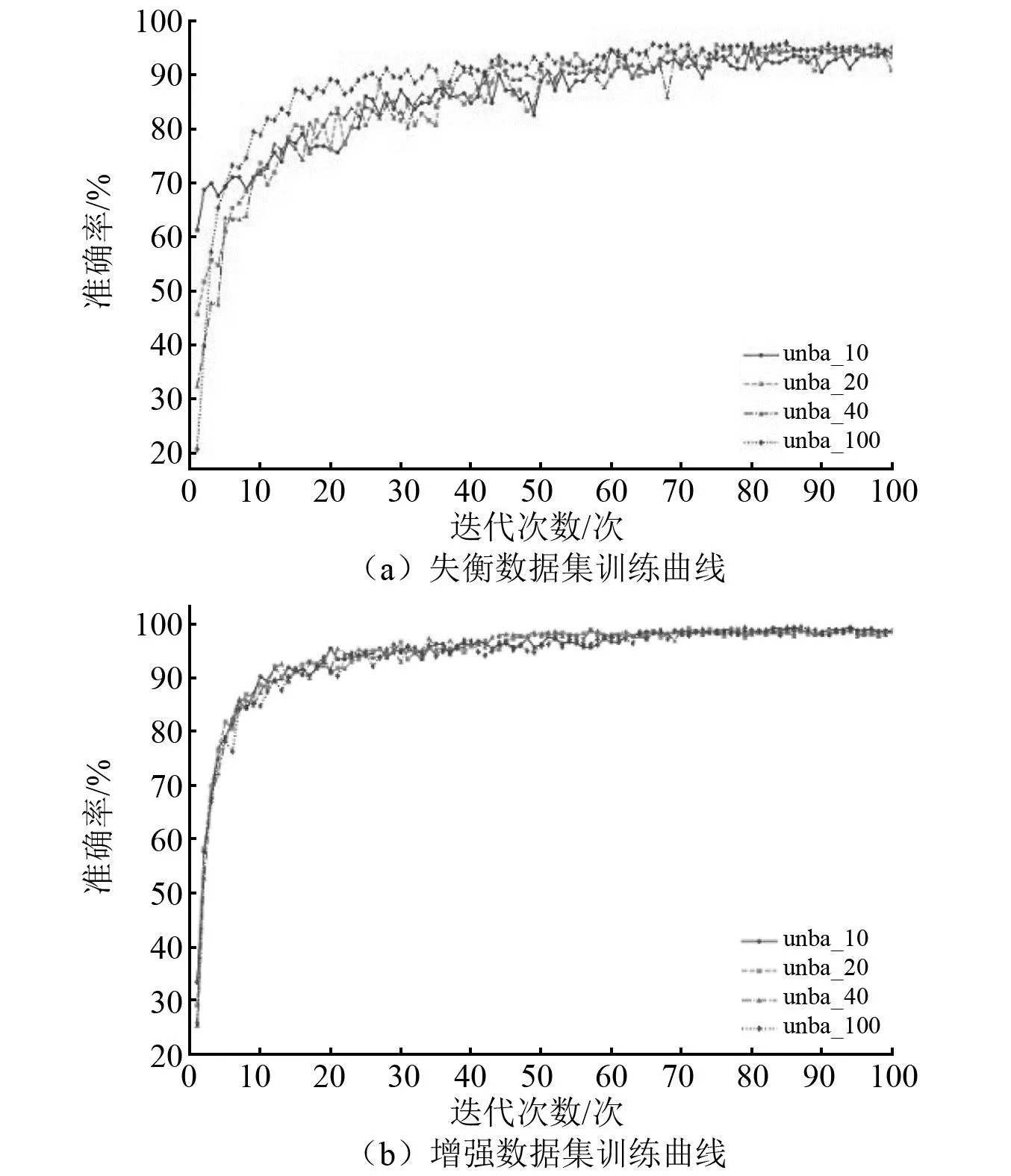
图7 SwinNet网络训练曲线Fig.7 SwinNet network training curves

为了验证MCIDA算法拥有较强的泛化能力,使用4组增强数据集来对AlexNet、ResNet、M1DCNN[27]、MTSC-CNN[28]故障诊断模型进行训练,使用原始数据集来作为测试集。本文提出的SwinNet网络与其他4种对比算法的测试集结果如表3所示。

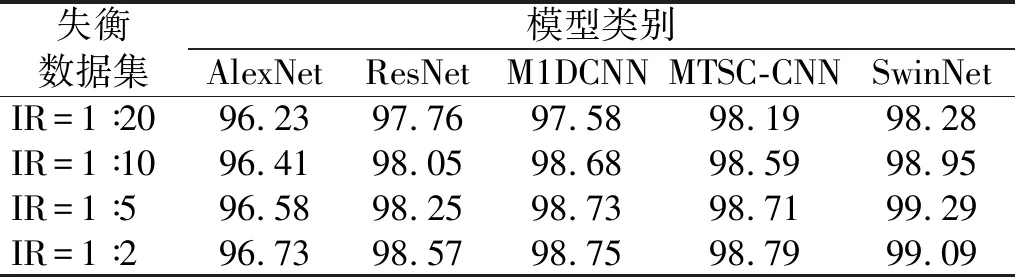
表3 不同故障诊断模型的测试集精度Tab.3 Test set accuracy of different fault diagnosis models

由表3可知所有模型使用测试集进行测试的诊断精度均能够达到96%以上,这充分证明了MCIDA算法的普适性,大多数深度学习故障诊断模型通过该增强算法增强后的增强数据集进行训练后都可以获得不错的故障诊断精度,其中SwinNet网络在第3、第4组测试集中的精度更是达到了99%以上。

SwinNet网络模型的测试集分类结果可以通过图8的混淆矩阵更加直观的展示。结合数据集的描述可以发现SwinNet网络在4组不同测试集进行测试的结果中分别只有5、5、4、10个状态类别被错误的分类。

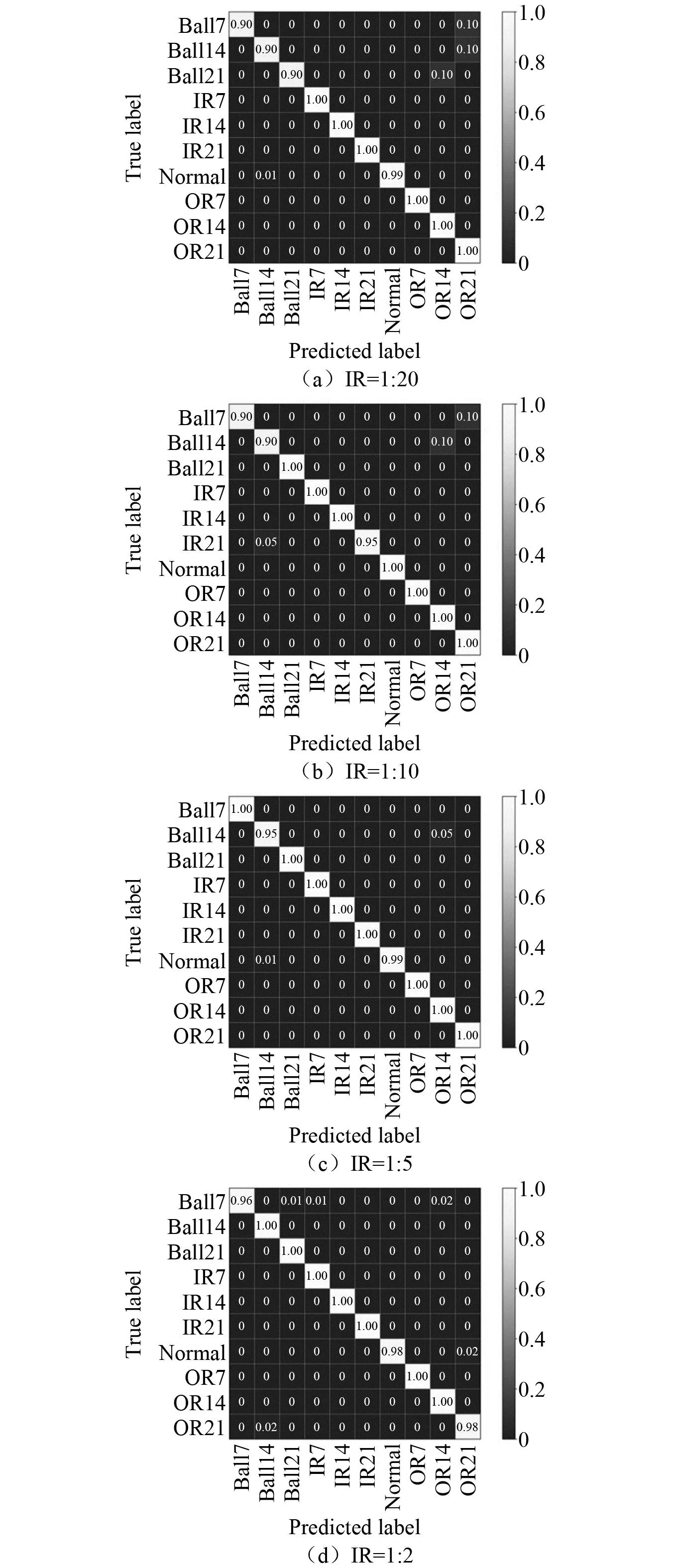
图8 4组测试集混淆矩阵Fig.8 Confusion matrices for the 4 test sets

3.3 噪声环境测试

机械设备在实际运行过程中通过传感器采集到的振动信号往往携带环境噪声,而CWRU数据集的振动信号所包含的噪声级别还达不到“强噪声”的程度。考虑到机械设备运行环境中,许多噪声源的统计特性近似为高斯分布,而高斯白噪声作为一种随机噪声能够涵盖多种频率范围内噪声成分,因此使用高斯白噪声来模拟真实环境中的复杂噪声是一种较为有效的方式。为了评估SwinNet网络在噪声环境下的诊断性能,在4组原始失衡数据集中分别添加信噪比为-4～12 dB的高斯白噪声,然后使用通过4组增强数据集进行训练的模型来进行抗噪试验。通过增强数据集训练的模型的抗噪测试验证结果如图9所示。

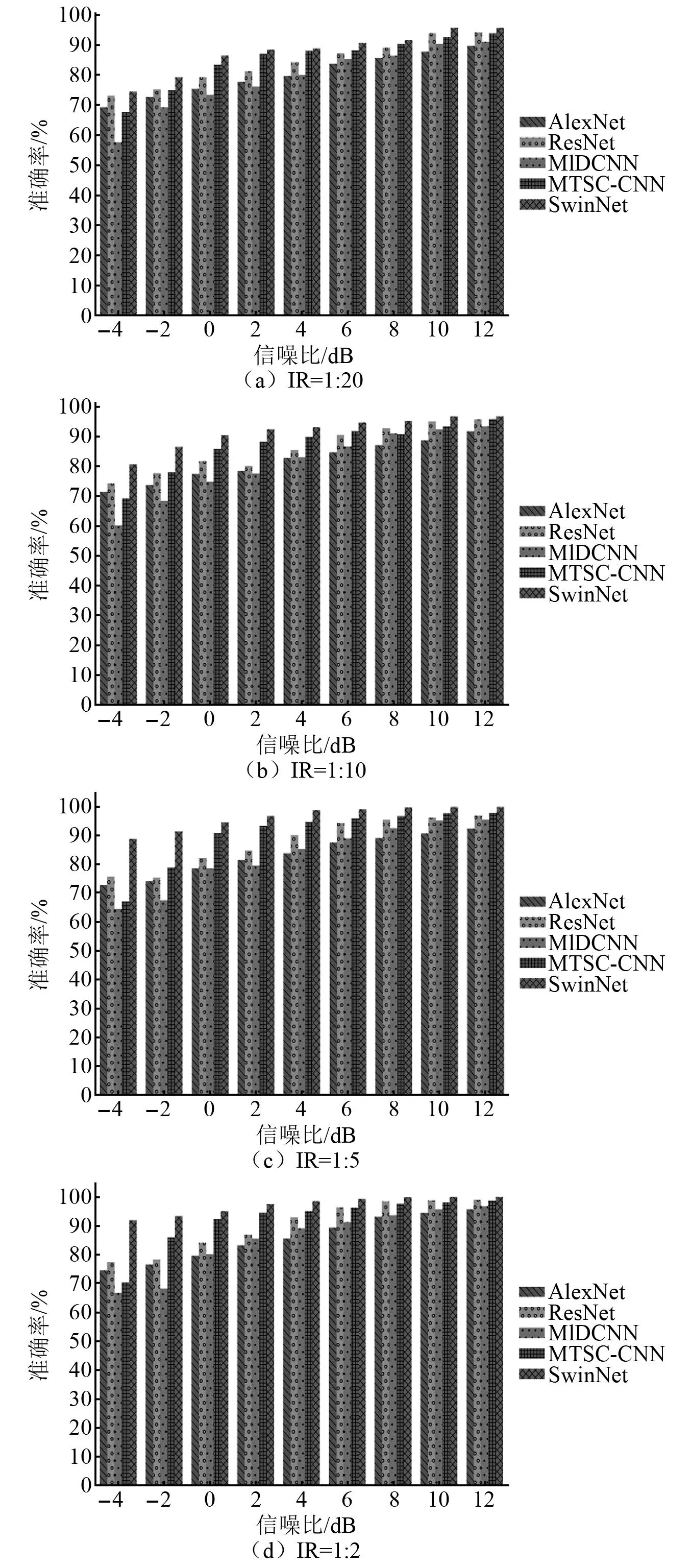
图9 噪声测试验证结果Fig.9 The results of noise testing verification

使用MCIDA算法增强IR为1∶20的失衡数据集,通过该增强数据集进行训练的模型抗噪测试具体值如表4所示。

表4 增强IR为1∶20的数据集训练的模型的噪声测试结果Tab.4 Noisy test results for a model trained on a dataset with an augmentation imbalance ratio of 1∶20

由图9(d)可知,通过MCIDA算法对轻微失衡数据集进行数据增强后再训练得到的模型的抗噪测试准确率最高,其中本文所提出的SwinNet网络在信噪比为-4 dB时可以获得超过90%的准确率,精度远远超过其他模型。随着失衡数据集的失衡程度升高,虽然所有诊断算法可以通过使用MCIDA算法来增强其故障诊断精度,但是模型在“强噪声”的影响下其精度还是会有不同程度的下降,通过图9(a)再结合表4数据可知本文所提出的SwinNet网络的故障诊断稳定性比其他所有模型都好。即使受到原始数据类别严重失衡与噪声环境干扰的双重影响,SwinNet网络的诊断精度仍然高于其他模型,达到了74.45%。

为了验证SwinNet网络在更加极端的噪声环境中诊断的有效范围,针对失衡比值为1∶5与1∶2的原始数据集进行数据增强后进行训练的SwinNet网络进行更多信噪比场景下的抗噪测试,其结果如图10所示。

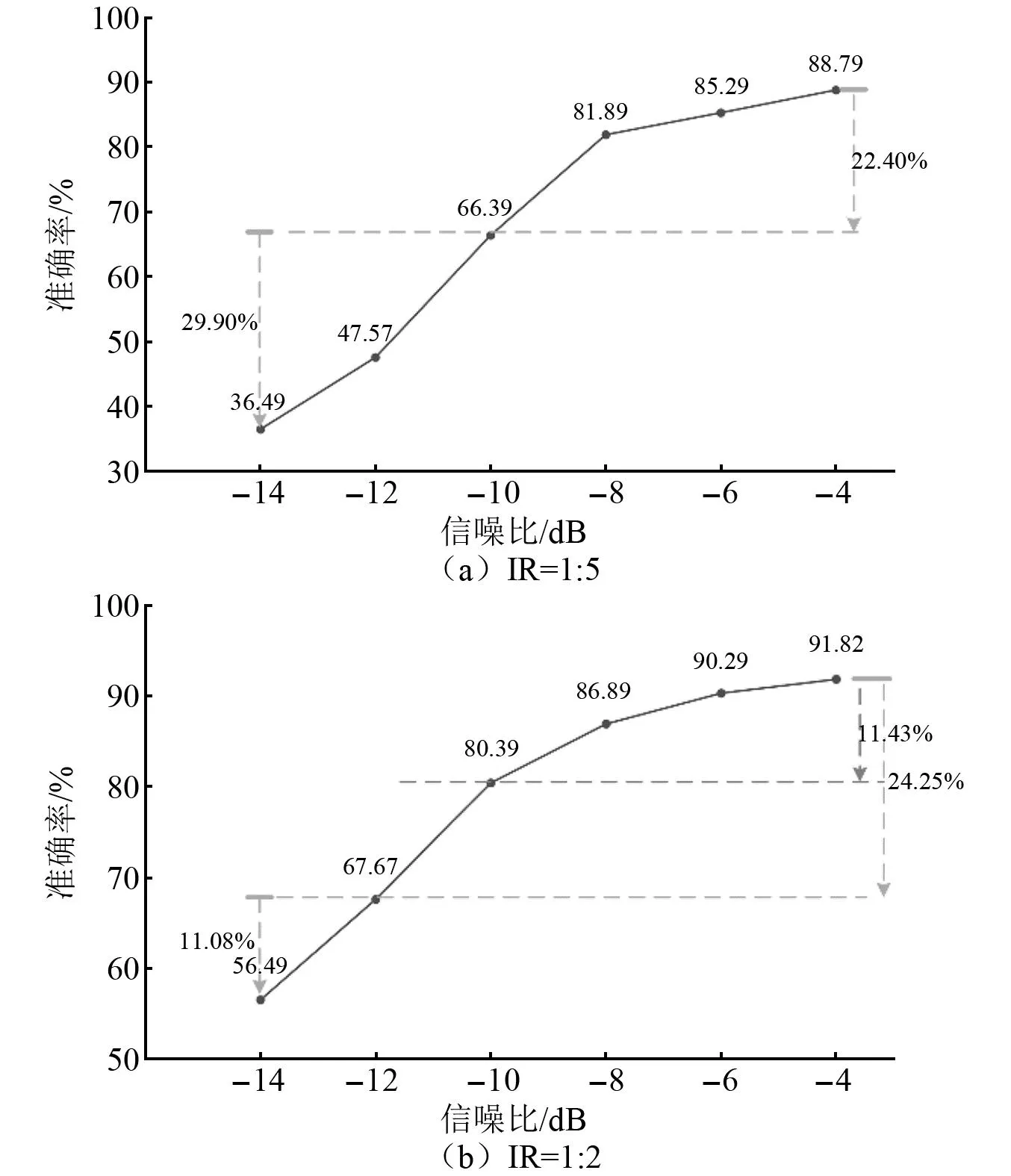
图10 SwinNet网络极端噪声环境测试结果Fig.10 Testing results of SwinNet network under extreme noise environment

由图10(a)可知,随着噪声的增加,SwinNet对故障信号的提取能力减弱。当信噪比为-10 dB时,其诊断精度相比于信噪比为-4 dB时下降了22.4%,但此时的精度可以达到66.39%,仍然是可以接受的水平,随着信噪比下降到-14 dB,其诊断精度迅速下降了29.9%,可以认为此时SwinNet网络不再具备故障诊断能力。由图10(b)可知当原始数据集只有轻微失衡时,使用数据增强后再训练获得的SwinNet网络在信噪比为-12 dB时的诊断精度为67.57%,仍然具有较强的诊断能力。究其原因是因为SwinNet模型拥有MSLRF层可以充分的提取二维时频图像的低维特征,同时拥有Swin Transformer编码器的局部窗口机制与移动窗口机制,可以更加关注当前像素点相邻的像素点,减少对噪声或者异常数据点的关注,进一步提高模型的泛化能力。

3.4 噪声标签测试

在实际的故障数据采集过程中,经常由于人为操作失误导致某些样本被标记上错误的标签,这种错误标签被称为噪声标签。为了验证SwinNet网络在样本集轻微失衡且混入了噪声标签的情况下仍然具有很好的诊断精度,使用3.2节中的失衡比值为1∶2的失衡数据集来作为该试验的原始数据集。由于实际故障诊断中不可能出现某类样本集存在大量噪声标签的情况,因此在这里对原始数据集按照3∶1∶1的比例划分出训练集、验证集、测试集后,将不添加噪声标签的训练集记为A,而按照5%、8%、10%的噪声标签率(Label Noise Rates,LNR)对训练集中的样本进行替换后获得的3组含有噪声标签的训练集记为B、C、D,具体划分细节由表5给出。

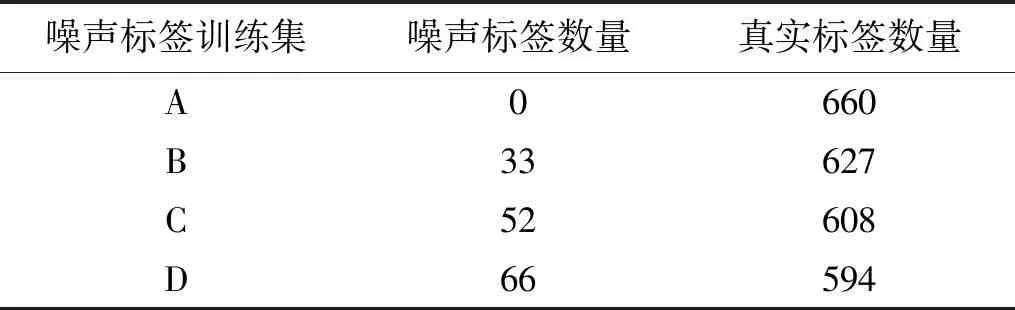
表5 4组噪声标签训练集具体划分展示Tab.5 4 sets of noise label training set specific division display

将SwinNet网络与对比模型在4组含有不同噪声标签数量的训练集中进行训练,使用不含噪声标签的测试集对网络模型进行测试,各个模型的测试集对比结果如表6所示。从表6中的结果可知在样本集轻微失衡的情况下,错误的标签占比确实会在一定程度上影响模型的故障诊断精度。随着训练集中噪声标签数量的增加,各个模型的诊断精度都呈现明显的下降趋势。结合图11与表6可知,本文所提出的SwinNet网络在样本集轻微失衡且训练集中混入了噪声标签的情况下诊断性能仍然表现优异。即使在训练集噪声标签率为10%的情况下,其诊断精度仍然达到了98.12%,远超过了其他的故障诊断模型的诊断精度。

表6 不同噪声标签率下训练的模型的测试集对比结果

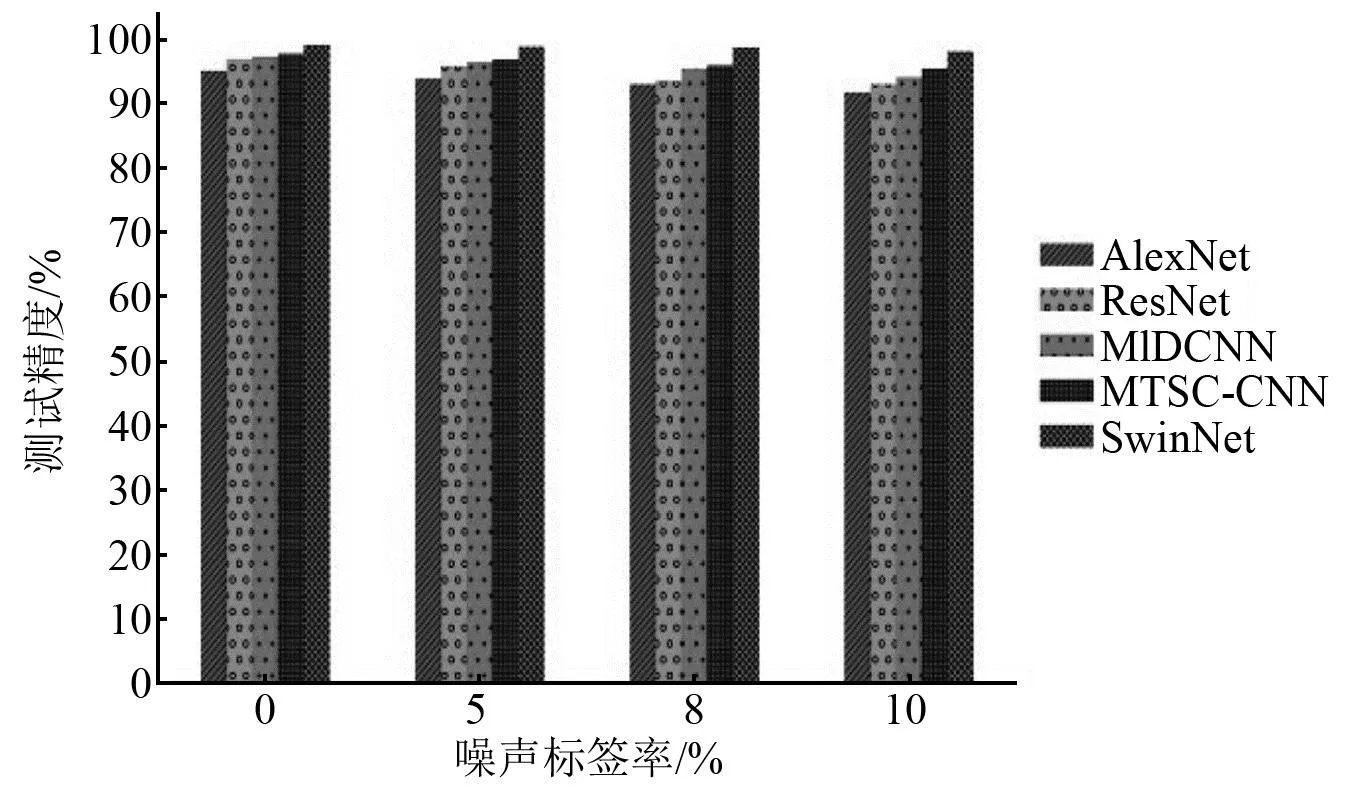
图11 不同噪声标签率结果对比Fig.11 Comparison of results with different noise label rates

为了更加直观地观察SwinNet网络的故障诊断效果,采用t-SNE技术可视化处理测试集样本,获得测试集的样本特征分布如图12所示。其中,图12(a)是使用不含噪声标签训练集训练的SwinNet网络对测试集进行分类后的可视化特征分布情况,图12(b)～图12(d)分别是使用噪声标签率为5%、8%、10%的训练集训练的SwinNet网络对测试集进行分类后的可视化特征分布情况。

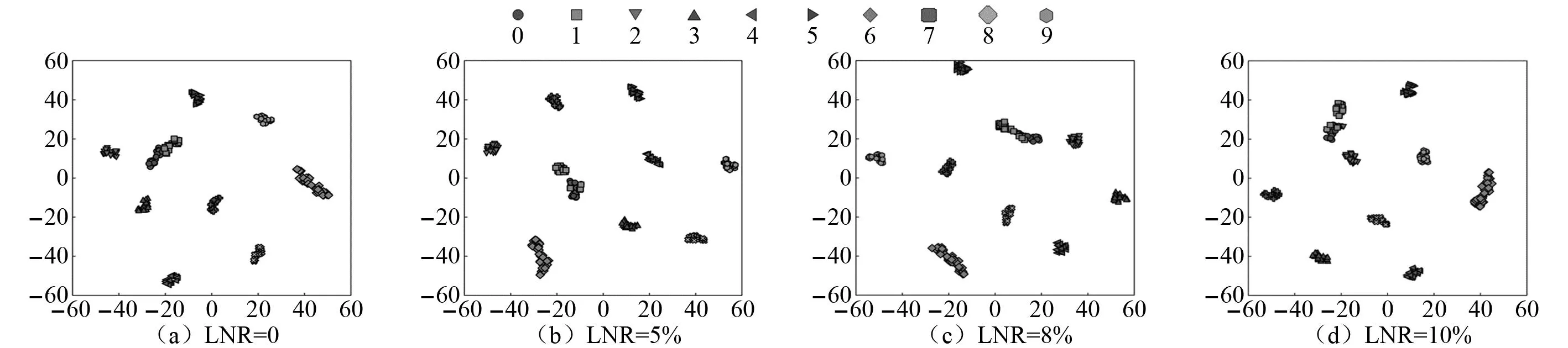
图12 不同噪声标签率下t-SNE特征可视化显示Fig.12 t-SNE feature visualization display under different noise label rates

由图12可知,在样本集轻微失衡且训练集含有噪声标签的情况下,本文所提出的SwinNet网络仍然可以将测试集中的样本特征进行很好的分割。这充分说明了SwinNet网络优秀的故障诊断能力,该网络利用MSLRF 层对二维时频信号进行特征提取后,借助移动窗口自注意力机制对输入的图像特征进行全局信息的建模,让模型可以更好地学习到鲁棒的特征表示,从而进一步提高模型的鲁棒性。

4 结 论

针对在较为复杂的环境中对滚动轴承进行高精度的故障诊断问题,本文提出了一种将混合裁剪失衡数据增强算法与SwinNet网络进行结合的故障诊断方法。具体结论如下:

(1) 提出了一种混合裁剪失衡数据增强(MCIDA)算法,利用该算法可以很好地解决滚动轴承故障诊断领域存在的故障数据类别失衡问题。

(2) 提出了一种SwinNet故障诊断网络,该网络与MCIDA算法进行结合使用能够很好地应对诊断中存在的环境噪声干扰与噪声标签干扰问题。

(3) 本文在公开数据集上做了大量仿真测试。结果表明,与现有方法相比本文所提出的方法故障诊断精度相对更高。

虽然本文所提方法在一定程度上提高了滚动轴承的故障诊断效果,但是在针对变负载条件下滚动轴承故障诊断方面还要做进一步研究。