非堆积型多颗粒阻尼器等效力学模型及其减振性能分析
李小军, 田超杰, 黄绪宏
(1. 北京工业大学 城市与工程安全减灾教育部重点实验室,北京 100124;2. 青岛理工大学 土木工程学院,山东 青岛 266520)
作为一种无源的被动控制装置,颗粒阻尼技术最早起源于航空及机械振动控制领域,其通过将多个金属或非金属颗粒材料按某一填充率放入受控结构的特定空腔内进行构造。当结构发生振动时,通过颗粒之间及颗粒与容器之间碰撞、摩擦,消耗、存储并传递振动能量,以此达到结构减振控制的目的。因其具有减振效果好、作用频带宽、造价低廉等优点,有望在工程结构振动控制领域中得到较好的应用。
虽然颗粒阻尼技术具有较好的应用前景,然而对其复杂的非线性特性认识不足限制了其在实际工程结构中的推广应用,深入揭示其减振性能及影响因素成为研究的关键。Papalou等[1-2]设计进行了简谐激励及随机振动下颗粒大小、附加质量比、容器尺寸及外部激励强度对减振性能影响的振动台试验。研究结果表明,相较于单颗粒冲击阻尼器,多颗粒形式明显降低了噪音,并改善了阻尼器减振效果受外部激励影响的鲁棒性。闫维明等[3-5]系统分析了多颗粒阻尼器 (multi-particle damper, M-PD)物理参数对振动控制效果的影响规律,并对其在多层框架结构、多跨连续桥梁及沉管隧道中的应用进行了探索。通过试验研究,其进一步指出M-PD在土木工程领域宜采用非堆积形态进行构造,即非堆积型多颗粒阻尼器(non-packed particle damper, NPPD)。Papalou等[6]通过开展大理石柱缩尺模型振动台试验,讨论了附加质量比、阻尼器布置位置、颗粒大小等参数对M-PD减震性能的影响。鲁正等[7-8]对附加缓冲材料的M-PD减震性能进行了讨论,并与悬吊式调谐质量阻尼器减震性能进行对比,试验结果表明,同等条件下M-PD的减震性能优于悬吊式调谐质量阻尼器。Fu等[9-10]进行了不同颗粒级配下M-PD减振效果试验研究,并与调谐液体质量阻尼器进行对比,结果显示颗粒阻尼器作用频带宽度更广。上述试验研究初步探明了M-PD减振性能及机理,为数值分析及相关研究提供了试验数据及支撑。
在试验基础上,开展力学模型研究,进行数值仿真分析是进一步明确M-PD减振性能的重要手段。Yao等[11]采用近似线性化的方式将竖向激励下调谐型颗粒阻尼器等效为竖向双重调谐质量阻尼器,并对该力学模型进行了试验验证,结果表明该力学模型能够合理预测阻尼器减振性能。许维炳等将调谐型颗粒阻尼器等效为双重调谐质量阻尼器,并基于该模型进行了参数分析及阻尼器优化设计,优化后阻尼器被应用到多跨连续桥梁当中。上述采用近似线性化所建立的等效力学模型一定程度上反映了M-PD减振性能,但其并不能较好地反映颗粒群与结构碰撞过程中的非线性特性,为此部分学者引入碰撞间距建立对应力学模型。基于等效前后质量及空隙率相等且材料特性及形状不发生变化的原则,鲁正等[12]基于接触单元法将M-PD等效为单颗粒力学模型,在随机激励下讨论了碰撞间距、附加质量比及碰撞阻尼系数等对减振性能的影响规律。采用相似的等效原则,Yan等[13]通过引入碰撞恢复系数考虑颗粒群与容器之间的碰撞效应,建立应对的力学模型,并基于该模型进行了参数影响分析及耗能机理分析。黄绪宏等[14]在上述等效单颗粒力学模型研究基础上,进一步引入惯容元件,考虑颗粒群滚动对M-PD减振效果的影响,建立了考虑惯容的等效单颗粒模型(equivalent inertia single-particle model, EISM),并基于EISM进行了自由振动、简谐激励及地震作用下减振效果分析及能量变化规律分析。
上述考虑碰撞效应所建立的力学模型进一步明晰了M-PD非线性特性,然而目前所建立的力学模型仍然存在不足之处,包括基于碰撞恢复系数所建立的力学模型并不能反映颗粒群与结构碰撞时的时间效应,且现有商业有限元软件尚未给出与其对应的数值仿真分析方法,限制了该模型的应用;基于接触单元法建立的力学模型并不完善,尚未考虑颗粒群的惯容属性,且其物理参数取值原则并未明确。
为进一步揭示M-PD的减振机理和性能特征,本文以NPPD作为研究对象,在现有EISM研究基础上,建立基于接触单元法的等效惯性单颗粒力学模型(equivalent inertia single-particle model based on contact element method, EISM-CE),并基于Runge-Kutta算法给出对应数值仿真分析流程。设计进行NPPD-单层钢框架模型振动台试验,提出对应EISM-CE的参数取值原则,并进行等效模型试验验证及对比分析。最后,在最优填充率下对比分析NPPD减振性能及能量变化规律。
1 基于接触单元法的等效单颗粒模型
1.1 等效单颗粒模型的提出
假设运动过程中颗粒群集中排布,考虑非碰撞阶段颗粒群滚动及其他非线性特性对NPPD(如图1所示)减振性能的影响,黄绪宏等引入惯容元件建立对应EISM,见图1(b)。其中:q为惯容系数,q越大,表明颗粒群与结构之间越难发生相对运动;d为颗粒群等效集中质量m1与结构之间的碰撞间距;e为碰撞恢复系数。
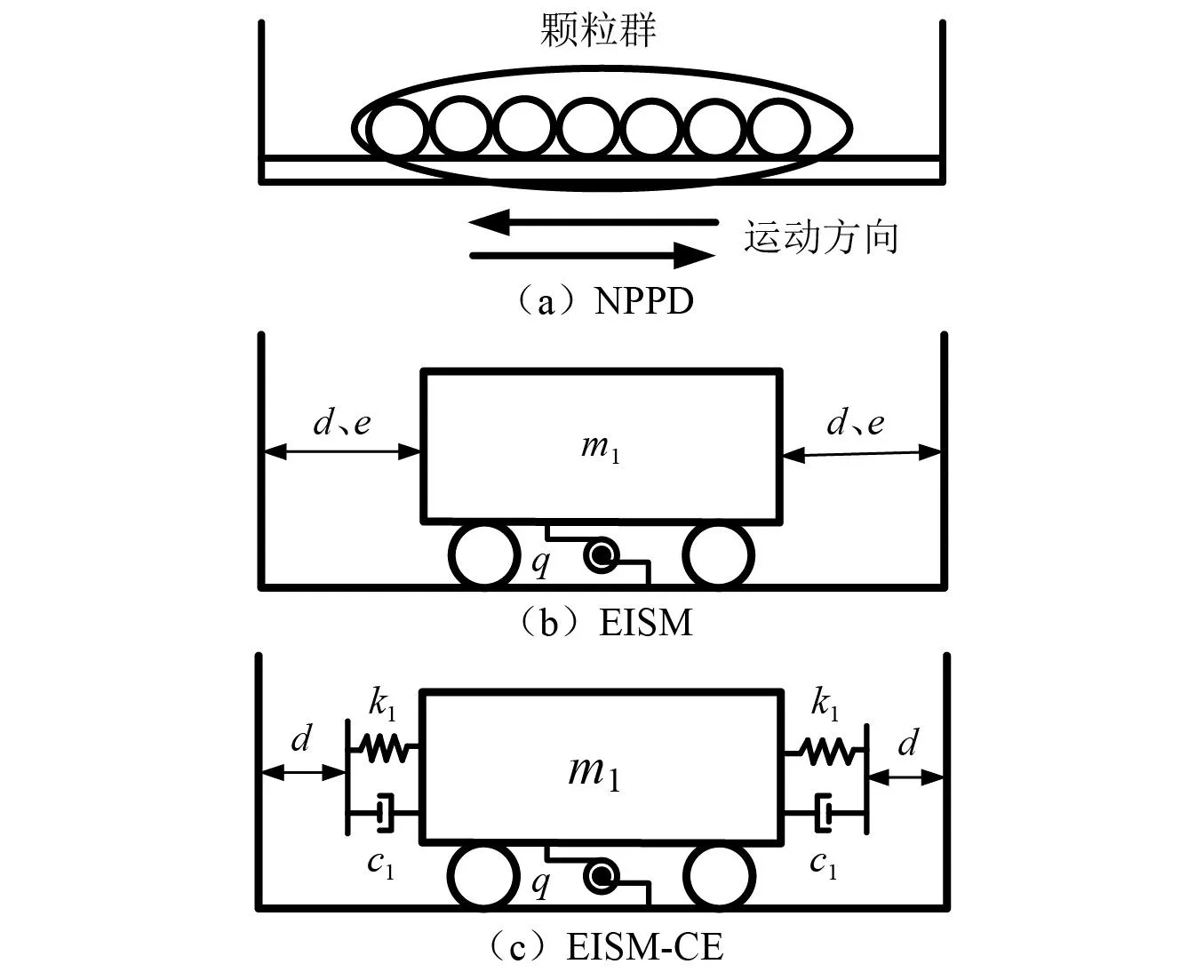
图1 等效单颗粒力学模型Fig.1 Equivalent single particle model
为进一步考虑碰撞过程中的时间效应,在EISM研究基础上,本文基于接触单元法提出对应EISM-CE模型,见图1(c)。与EISM相比,EISM-CE通过等效碰撞刚度k1及等效碰撞阻尼c1考虑碰撞过程中的颗粒群与结构之间的相互作用,其中k1反映碰撞过程中颗粒群与容器之间动量交换的能力,c1反映碰撞过程颗粒群与容器之间碰撞、摩擦所具有的耗能能力。
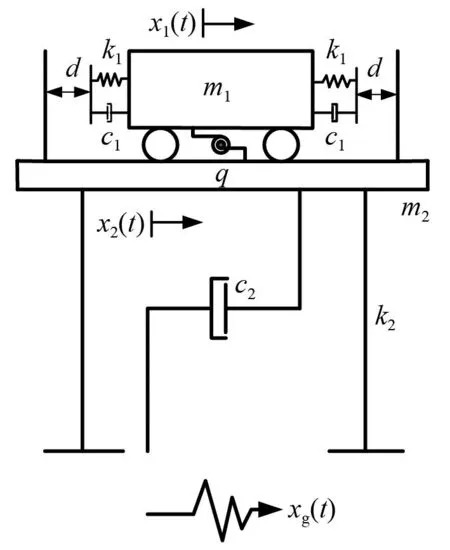
图2 单自由度EISM-CEFig.2 Single degree of freedom EISM-CE
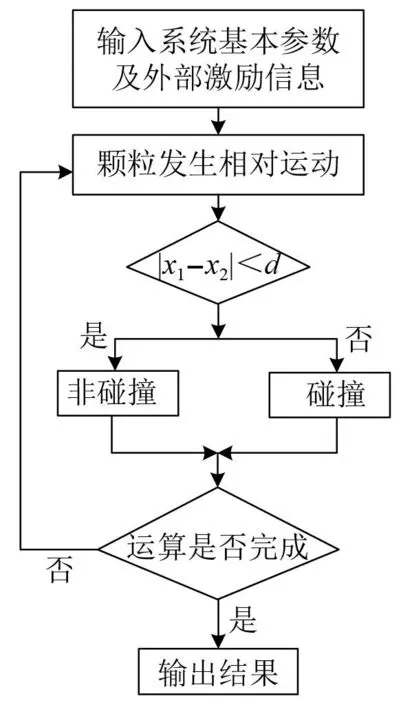
图3 数值仿真流程Fig.3 Flow chart of simulation
1.2 未碰撞阶段体系运动方程
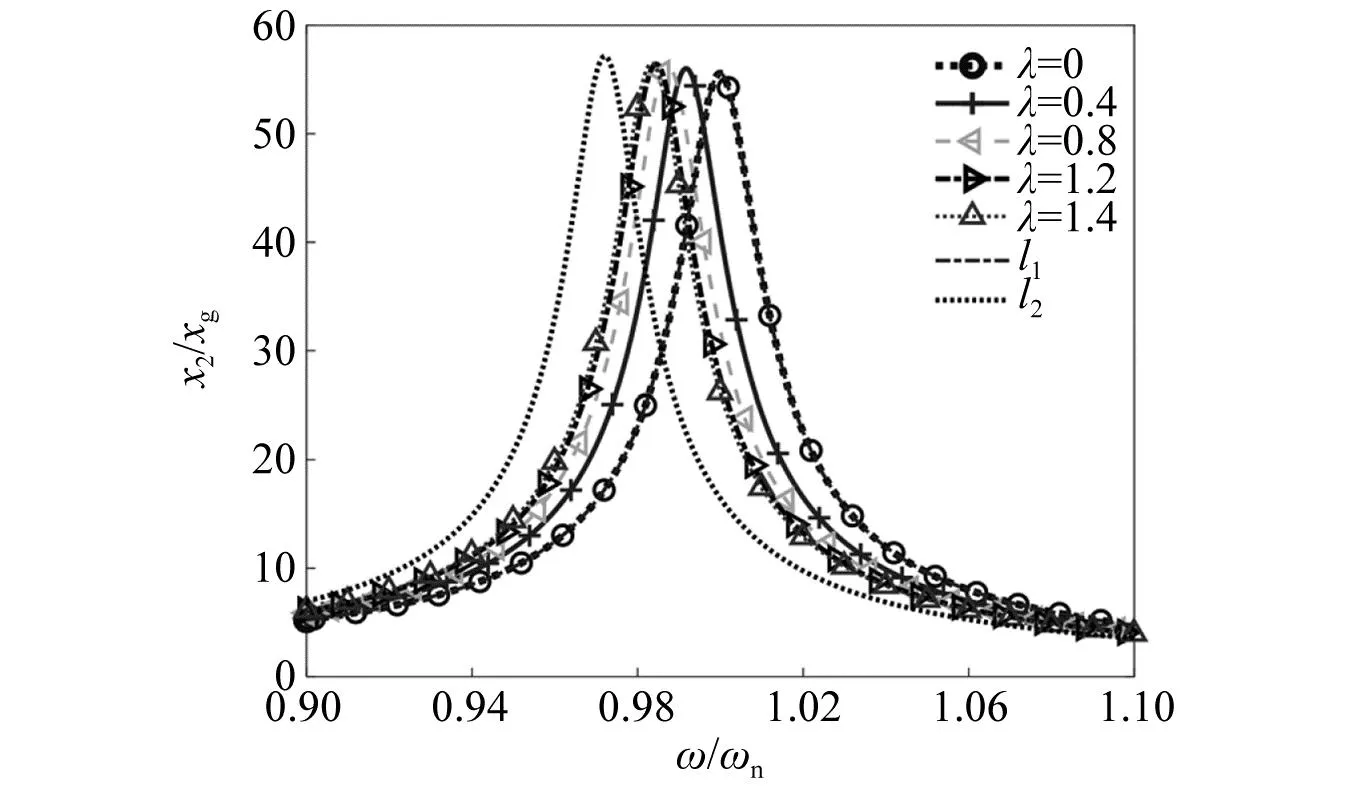
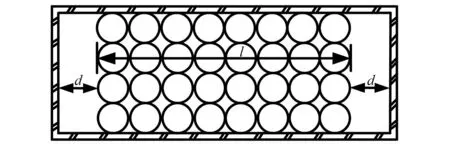
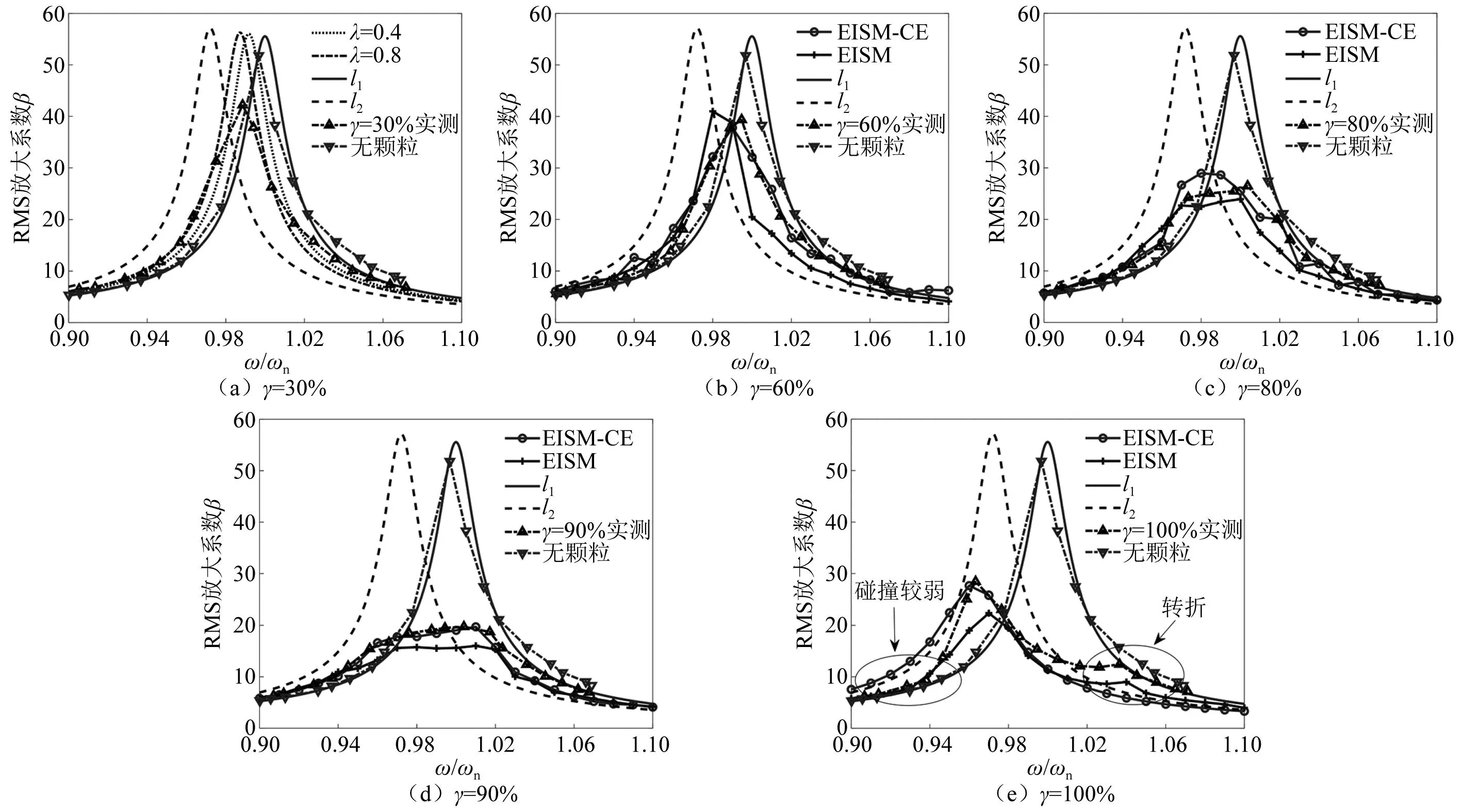
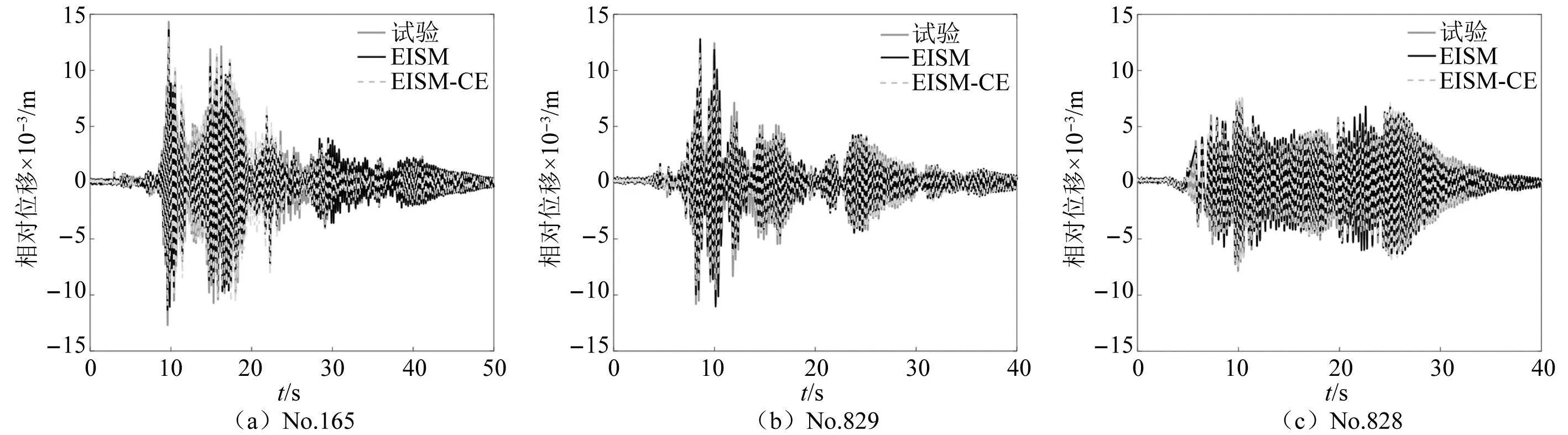
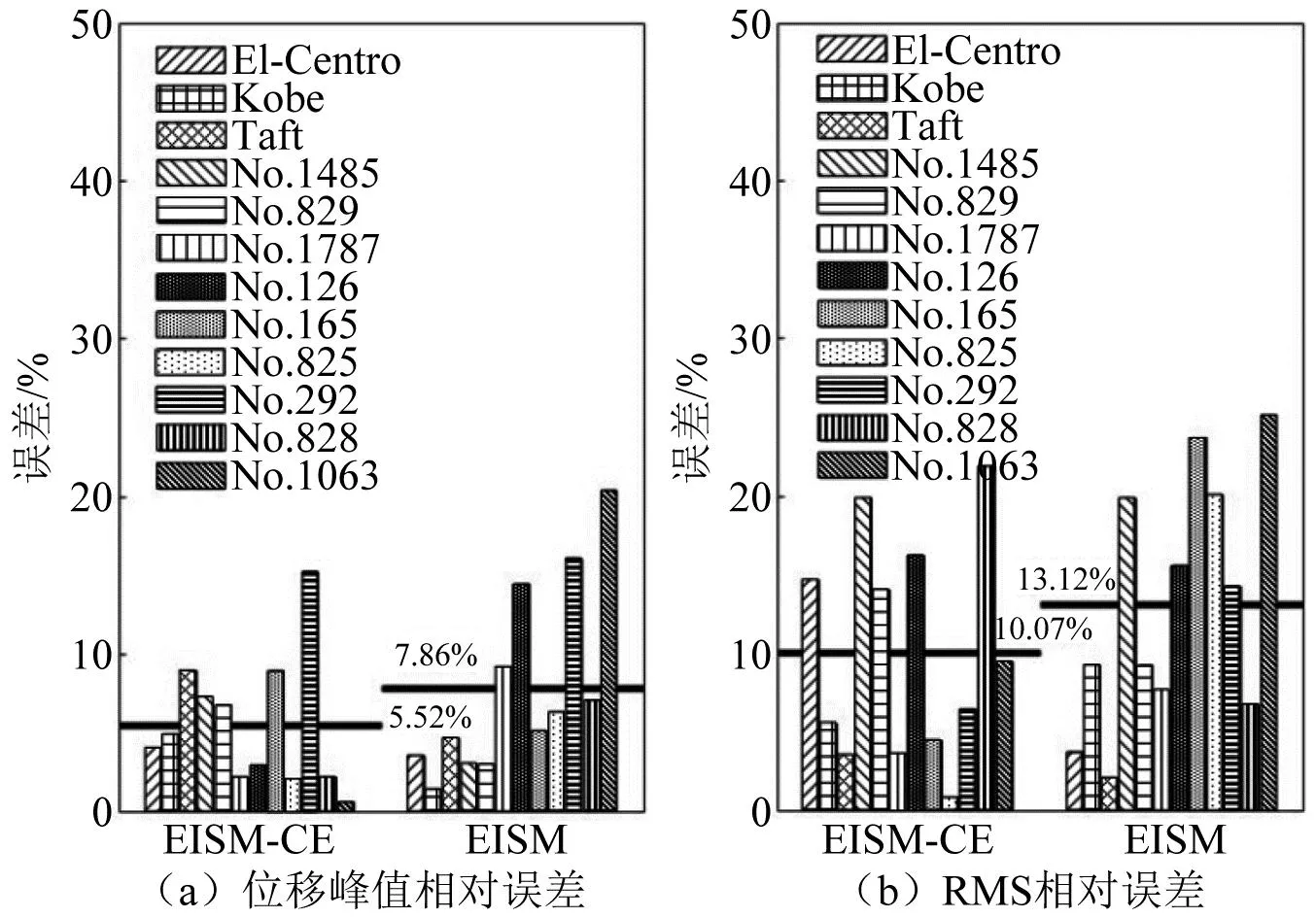
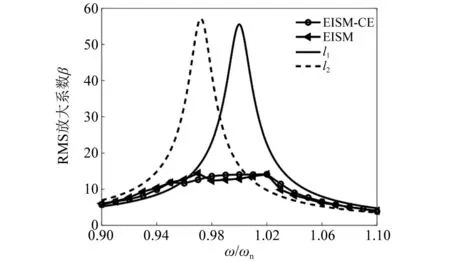
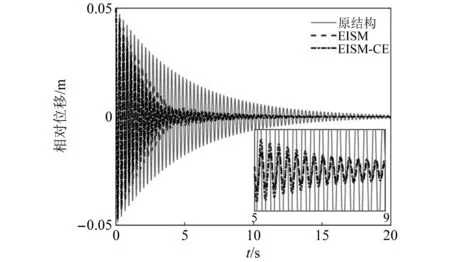
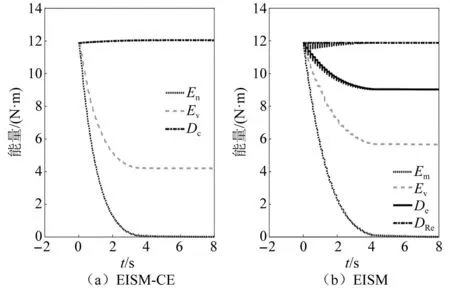
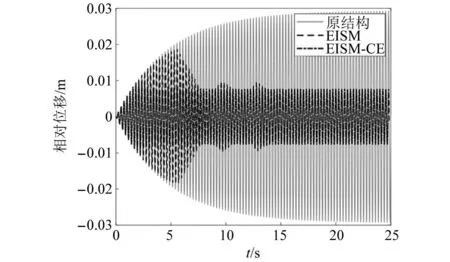
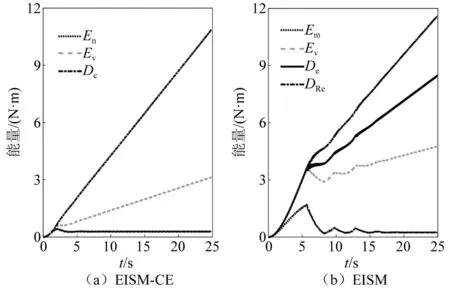
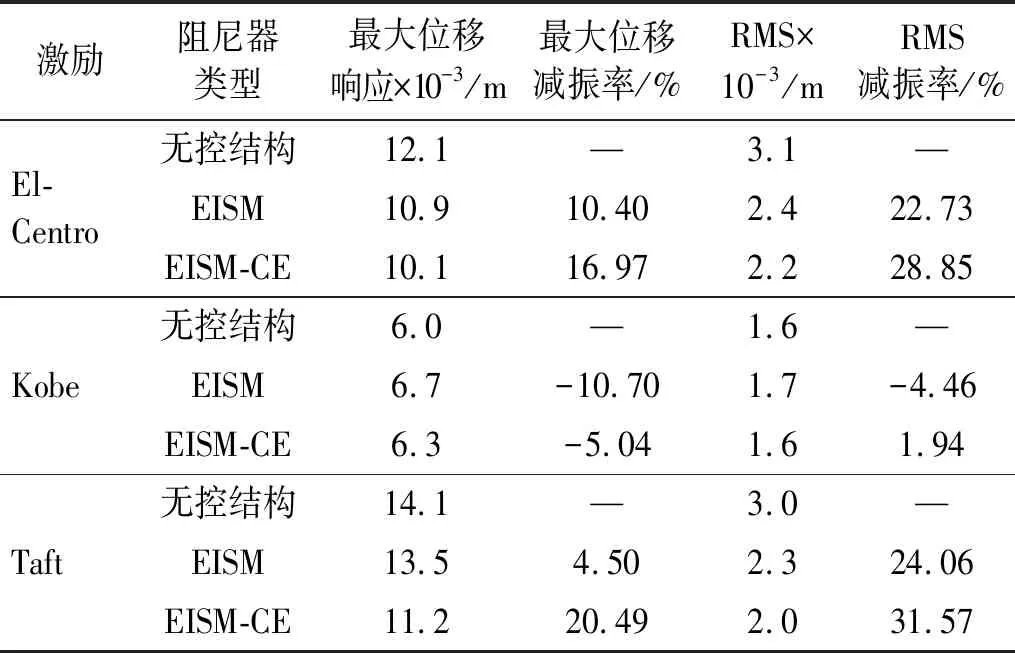
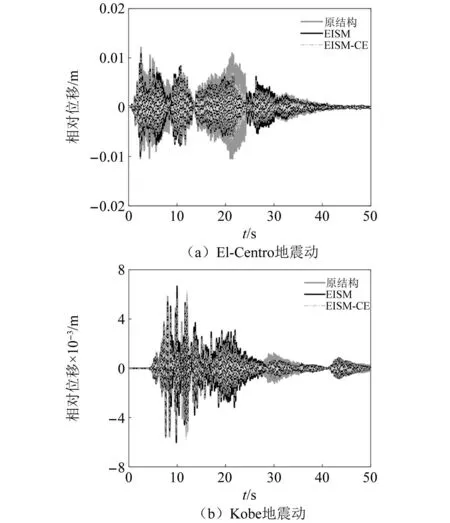
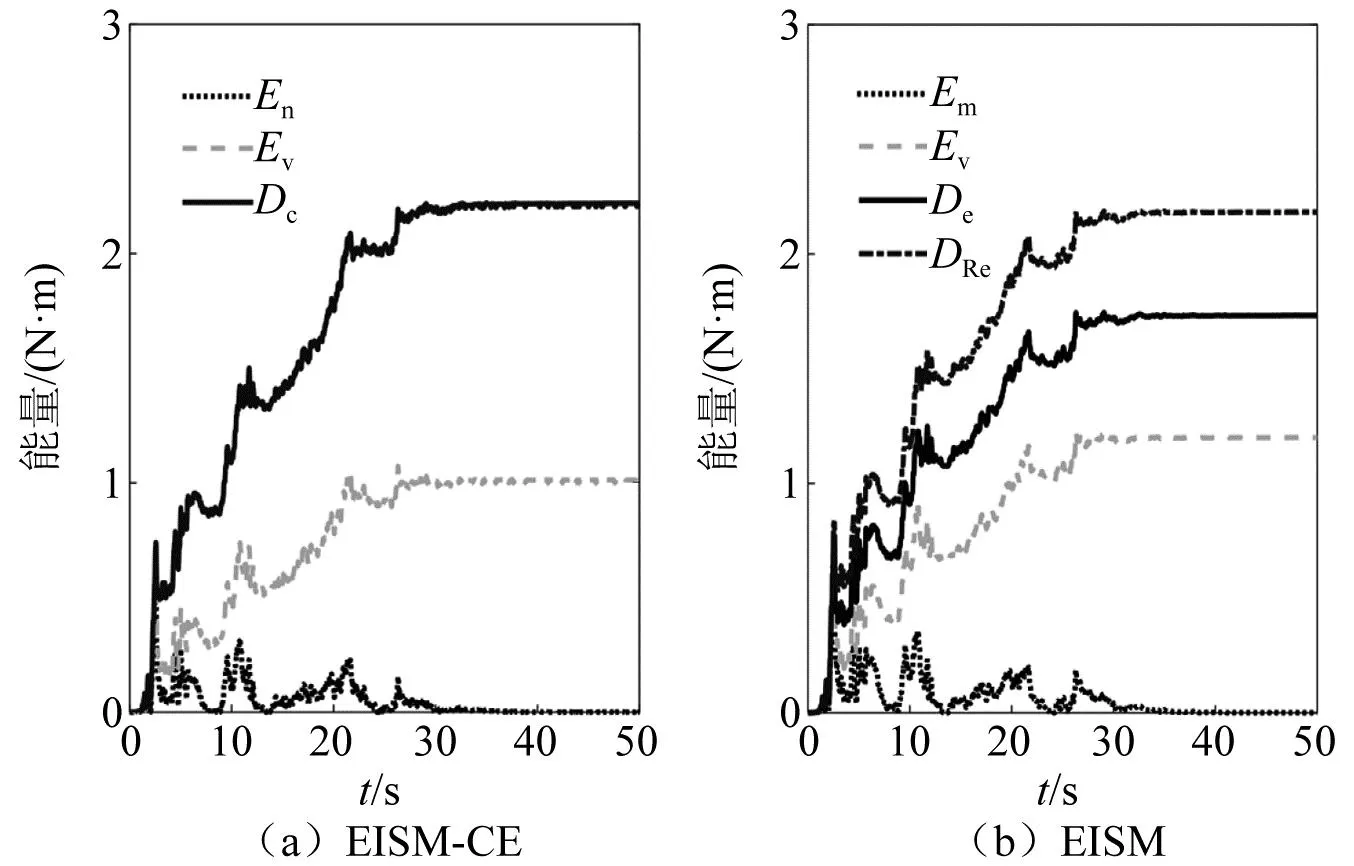
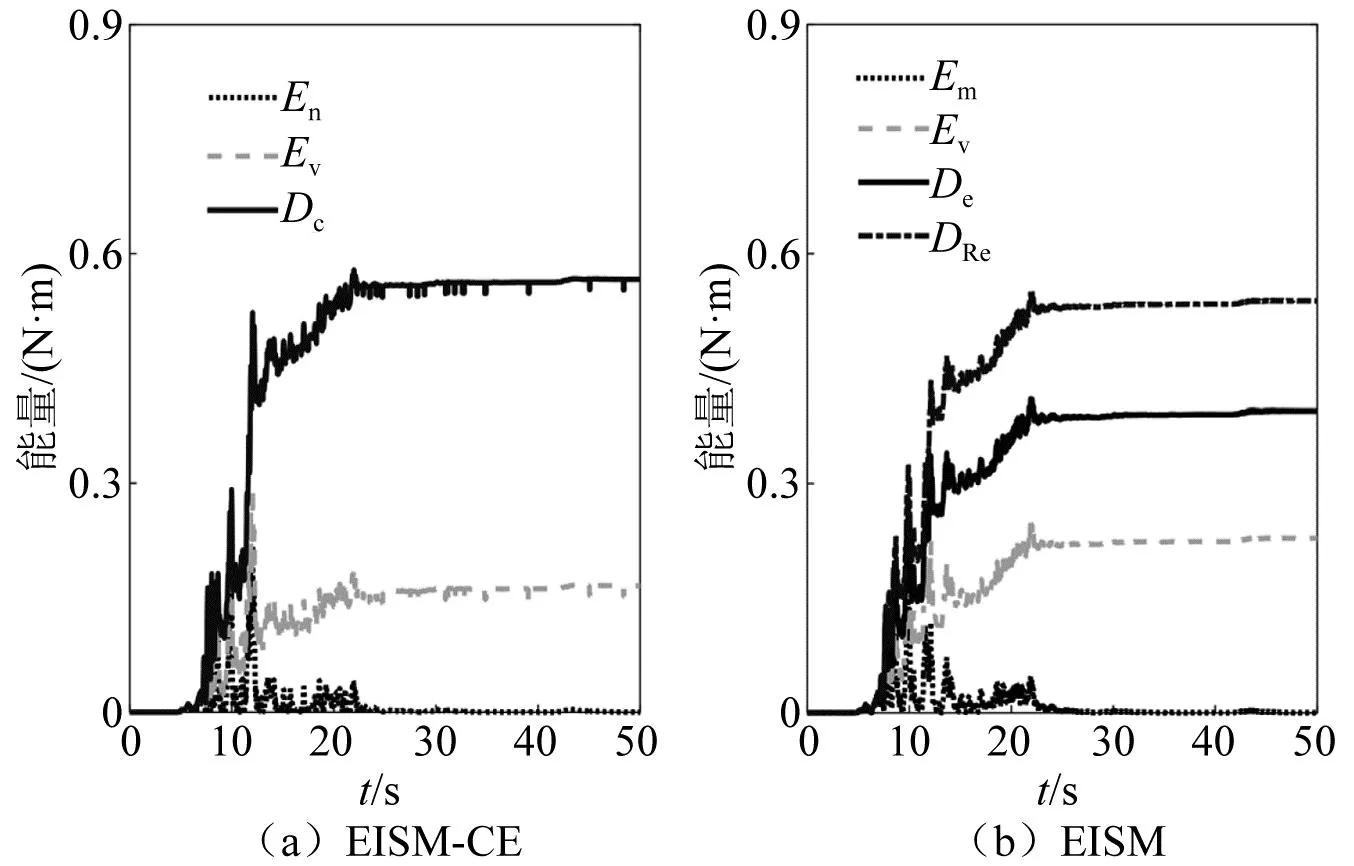
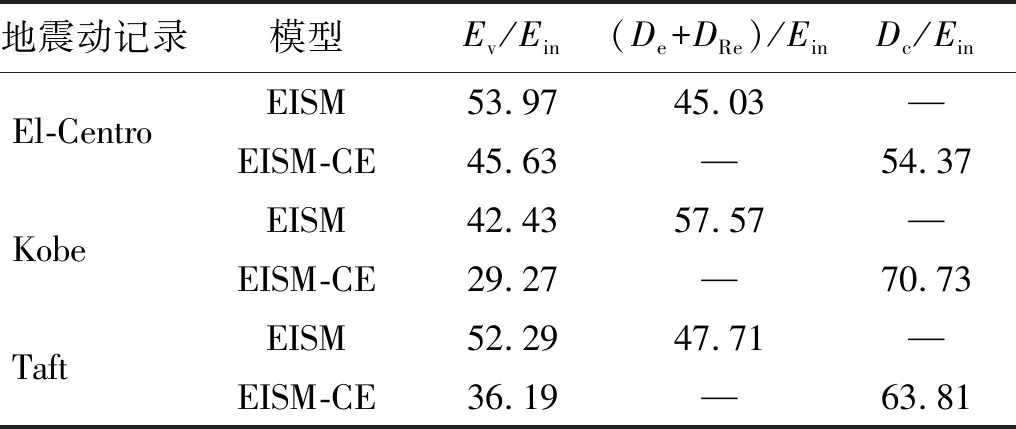
当阻尼颗粒与结构未发生碰撞时时(|x1-x2| (1) 进行拉普拉斯变换可得结构响应放大系数 (2) (3) 取μ=5.8%,λ对结构绝对位移放大系数频响曲线的影响如图4所示。图4中:l1对应原结构位移放大频响曲线;l2对应附加质量比5.8%所对应的位移放大频响曲线。由图4可知,随着λ的增加,结构位移放大系数频响曲线逐渐向较低频率移动,且受λ增加影响的灵敏度逐渐降低。当λ趋于无穷大时,位移放大系数频响曲线与l2重合,此时认为颗粒与结构同为一体,不发生相对滚动。 图4 结构位移频响曲线Fig.4 Frequency response curve of structural displacement 结构碰撞是一种高度复杂的非线性过程。本文采用接触单元法模拟颗粒与容器壁之间的碰撞过程,当冲击质量块m1与结构m2发生碰撞后(|x1-x2|≥d),由D’Alembert可得 (4) 式中, sign(·)为符号函数,其满足 (5) 为验证力学模型的合理性,清晰NPPD减振性能,本文设计进行NPPD-单层钢框架模型振动台试验,试验装置布置如图5所示。振动台的各项性能参数指标如表1所示。结合振动台台面尺寸,并考虑假定的结构基本自振周期需求,本试验设计框架顶部钢板尺寸为500 mm×500 mm×5 mm;柱高为800 mm,横截面尺寸为50 mm×5 mm,并沿柱高包裹高聚合物材料以提高框架阻尼比;顶板上放置颗粒腔体,腔体与顶板采用8 mm螺栓进行固接,腔体垂直于振动方向宽为300 mm,沿振动长度设置滑道以调节两侧碰撞板的间距,进而控制颗粒填充率。实测钢框架质量为17.2 kg,结构基本频率ω0=3.75 Hz,结构附加阻尼比为0.9%。试验中,阻尼颗粒取直径8 mm钢珠,μ=5.8%,依次进行简谐激励及地震动作用下的振动台试验研究。 图5 振动台与试验结构模型Fig.5 Shaking table and test structure model 基于等效前后质量相等,材料及形状保持一致的原则,Papalou等[15-16]提出M-PD对应等效单颗粒力学模型的等效原则,然而该种等效方法可能并不适应于NPPD。为此黄绪宏等依据颗粒等边三角形排列的形式计算两侧碰撞间距。为充分考虑颗粒群碰撞过程中的时间效应,借鉴上述等效原则,假设颗粒群按照四边形集中排布如图6所示,计算两侧d。图6中,l为集中排布后颗粒群长度。以本文对应的NPPD为例,不同填充率γ对应d取值如表2所示,其中γ取颗粒有序正方形排列投影面积与容器底面积之比。 表2 d取值Tab.2 Parameter values of d 单位:mm 图6 颗粒排布规则Fig.6 Particle arrangement rules 参考EISM,本文引入惯容元件考虑非碰撞阶段颗粒群滚动及其他非线性特性对NPPD减振性能的影响。由图4可知,λ对颗粒群运动过程中的非碰撞阶段影响显著,因此可以通过对比非碰撞阶段频响曲线确定λ值。当不考虑γ对λ的影响时,可近似通过低填充率下NPPD-SODF位移放大系数频响曲线确定λ的取值。 EISM-CE中k1及c1对NPPD减振性能具有显著的影响。k1能够近似反映碰撞过程中颗粒群与结构之间动量交换的能力,然而由于多颗粒复杂的非线性特性,目前仍未见k1详细的理论推导。在试验研究基础上,Huang等[17]提出了等效连体颗粒质量模型,并给出当γ=100%时两个非堆积颗粒群碰撞对应力学模型中等效连接刚度k0的取值 (6) 式中:μm2/(many)为沿振动方向颗粒群的排数;ma为单颗粒的质量,ma=4/3πr3ρa,r为颗粒半径;ε为孔隙率,对于四边形排布,取ε=0.365;w2为对应容器宽度的正方形面积;ny为单排颗粒数量,ny=w/(2r);ρa为颗粒材料密度。在k0基础上,为进一步考虑颗粒群排布及碰撞规则等对k1的影响,引入颗粒群碰撞形式修正系数ψ,对应k1计算公式为 k1=ψk0 (7) c1体现了颗粒与结构之间碰撞及摩擦耗能能力,其主要与颗粒碰撞恢复系数相关。在现有e经验取值基础上[18],考虑颗粒群排列形式对耗能能力的影响,取颗粒群对应e=0.2。由e与颗粒碰撞附加阻尼比ξ1的经验公式式(8)[19]及ξ1与c1的关系式式(9)可得到k1对应的c1。 (8) (9) 设计进行简谐激励下振动台试验研究,试验激励幅值取0.03g,调整两侧碰撞板间距依次进行30%、60%、80%、90%和100%填充率下减振效果分析。拾取不同激励频率下结构及振动台台面的位移响应,计算均方根(root mean square, RMS)(SRM)位移及位移均方根放大系数β作为减振效果指标,计算公式为 (10) (11) 式中:xi为第i个时间步的位移响应;N为时间步数,上标“s”和“t”分别为结构和振动台台面的位移响应。30%~100%填充率下结构位移响应均方根放大系数随激振频率比变化规律如图7所示。 图7 γ对减振效果影响分析Fig.7 The influence of γ on vibration reduction effect 由图7中试验结果分析可知: (1) 在当前试验参数设置下,当γ=90%时,减振效果最优,且减振作用频率范围较大。 (2) 当γ=30%时,由于碰撞间距较大,运动过程中,颗粒与容器壁基本不发生碰撞,无法发挥耗能能力,因此减振效果较差。频响曲线对比结果显示,由于颗粒群惯容属性的影响,与原结构频响曲线相比,γ=30%对应频响曲线明显位于较低频侧。 (3) 当γ<90%时,随着γ的增加,碰撞间距逐渐减小,颗粒与容器壁的碰撞次数逐渐增加,耗能能力逐渐增强,因此减振效果逐渐增加。当γ>90%时,随着γ的进一步增加,碰撞间距逐渐缩小,减振性能逐渐降低。在这一过程中,虽然颗粒与容器壁的碰撞次数逐渐增加,但冲击过程中碰撞间距减小,导致冲击力减小,颗粒群无法充分发挥耗能能力,致使NPPD减振效果降低。 为验证EISM-CE的有效性,进行试验验证,并与EISM进行对比分析。为此,首先确定λ的取值。由30%填充率对应频响曲线实测值(见图7(a))及理论解(式(2))可得λ=0.8,对应曲线相关系数R2= 0.969。在此基础上,考虑颗粒群排布规则对k1的影响,结合γ=100%对应频响曲线,基于数值仿真确定ψ=5,对应k1=1 712 N/m,c1=36.67 N·s/m。基于上述参数取值,假设颗粒群初始位于容器一侧进行数值仿真分析,对应不同γ下频响曲线拟合及实测对比如图7所示,分析结果表明: (1) 基于碰撞恢复系数所建立的EISM及本文提出的EISM-CE均能够较好地模拟NPPD减振性能,且EISM-CE拟合结果更加理想。 (2) 基于EISM-CE的减振机理分析结果表明,当γ<90%时,随着d的减小,等效冲击质量m1与结构之间的碰撞次数及剧烈程度逐渐增加,碰撞耗能逐渐增加,对应减振性能逐渐增加。当γ>90%时,随着d的减小,虽然碰撞次数逐渐增加,但碰撞剧烈程度逐渐降低,碰撞耗能逐渐减小,m1逐渐趋向于周期多次碰撞状态,对应减振性能逐渐降低。当γ=90%时,对应最优的减振性能。 (3) 力学模型详细对比分析结果表明,当γ=60%或γ=80%,ω/ωn较大时,EISM-CE与EISM拟合结果存在一定差异。EISM-CE拟合结果更加理想。究其原因,当激励幅值保持不变时,ω/ωn越大结构位移及速度越小,此时颗粒群碰撞的时间效应影响越显著。由于EISM未考虑时间效应,颗粒群与结构的碰撞次数增加,减振性能增加,位移放大系数曲线位于实测频响曲线下侧。相比之下,EISM-CE考虑了碰撞时间效应,拟合结果更加理想。 (4) 当γ=100%,β较小时,基于EISM-CE得到的频响曲线与实测曲线存在一定的差异。具体分析表明,当γ=100%时,运动过程中实际颗粒群排布较为密集,两侧存在一定的碰撞间距。当β较小时,颗粒群并未与结构之间充分碰撞,此时实测频响曲线更加趋向于l1。而对于EISM-CE而言,当γ=100%时,此时已存在明显的相互作用,这导致频响曲线模拟值与实测值存在一定误差。相比之下,由于EISM考虑了初始碰撞间距的影响,因此当β较小时EISM更加理想。需要注意的是,当ω/ωn=1.04左右时,此时实测频响曲线及EISM对应频响曲线存在转折现象,这亦是由于碰撞间距引起减振性能非线性所导致的。 地震激励具有复杂的频谱特性,在其作用下开展相关研究对于进一步认清力学模型的合理性具有重要意义。为此,选取γ=90%对应的NPPD,设计进行了地震作用下NPPD-单层钢框架振动台试验。考虑到颗粒阻尼器作用力特性及前期经验,除选取3条经典地震动记录(El-Centro地震动记录、Taft地震动记录和Kobe地震动记录)作为振动台输入外,另外参考ATC-63 project所记录的地震动记录,选取3条远场地震动记录(No.1485、No.829和No.1787),3条近场无速度脉冲地震动记录(No.126、No.165和No.825)和3条近场有速度脉冲地震动记录(No.292、No.828和No.1063)作为振动台输入,调整峰值加速度为0.20g进行振动台试验。3条不同类型地震动记录对应的结构实测及模拟位移曲线,如图8所示。EISM-CE模型和EISM模型对应位移峰值相对误差和RMS相对误差对比分析结果,如图9所示。 图8 地震作用等效模型试验验证Fig.8 Test verification of equivalent model under seismic excitation 图9 拟合结果误差统计Fig.9 Error statistics of fitting results 综合分析可知,EISM-CE拟合结果更加理想,其中EISM-CE的位移峰值相对误差为5.52%,RMS相对误差为10.07%。EISM的位移峰值相对误差为7.86%,RMS相对误差为13.12%。 以NPPD-钢框架模型作为研究背景,基于EISM-CE,进行减振性能对比分析,并结合能量发展讨论其作用机理。选取最优参数对应的NPPD作为研究对象。当激励幅值为0.03g时,对应EISM-CE的最优碰撞间距d0=4 mm。同一NPPD对应EISM参数为d=10.4 mm,e=0.25。最优NPPD参数设置下本文提出的EISM-CE及EISM对应β频响曲线如图10所示。由图10可知,2条频响曲线较为接近,这进一步说明了力学模型的合理性。在最优参数取值基础上,依次进行自由振动、简谐激励及地震动作用下的能量分析及减振效果分析。 图10 位移放大系数频响曲线Fig.10 Frequency response curve of β 初始结构位移取0.05 m,在最优碰撞间距下进行自由振动减振性能分析,如图11所示。由图11可知,自由振动下NPPD具有较好的减振效果,结构位移峰值呈非线性衰减。在振动初期,衰减速度较快,在中后期,衰减速度较慢。不同力学模型减振性能对比分析结果表明,振动前期EISM-CE结构位移峰值衰减速度更快,但到中后期,EISM的结构位移峰值衰减速度相对较快。原因分析表明,碰撞前期结构运动较剧烈,由于EISM-CE考虑了碰撞过程中的时间效应,系统耗能能力更加显著。中期后,EISM-CE中线性刚度k1与c1一定程度上限制了m1相对运动,因此耗能能力略有衰减。相比之下,中期后EISM中m1运动相对较为剧烈,因此耗能能力略微优于EISM-CE。 图11 自由振动下减振效果分析Fig.11 Analysis of vibration reduction effect under free vibration 为进一步分析系统能量耗散过程,基于运动方程建立系统能量方程,并与EISM进行对比分析。假设EISM-CE-SDOF与EISM-SDOF对应的外部输入能量分别为E1和E2,则系统能量分别满足式(12)和式(13)。 E1=Ev+Es+Ek+Dk+DR+Dc+Ds (12) E2=Ev+Es+Ek+Dk+De+DR+DRe (13) 式中:Ev为结构自身阻尼耗能;Es为结构势能;Ek为结构动能;Dk为颗粒群动能;De为颗粒群与结构垂直的碰撞耗能;DRe为因颗粒群转动引起的碰撞耗能;DR为颗粒群惯容对应的转动动能;Dc为颗粒群与结构之间碰撞阻尼耗能;Ds为颗粒群与结构之间的碰撞弹性势能。以上变量计算公式如下所示。 (14) (15) (16) (17) (18) (19) (20) (21) (22) 式中:vη为第η次碰撞时刻两个碰撞质量的相对速度;n为碰撞次数。 自由振动过程中系统能量累加曲线如图12所示。图12中:Em为EISM对应的累加系统机械能,为结构势能Es、结构动能Ek、颗粒群动能Dk、颗粒群惯容对应转动动能DR之和;En为EISM-CE对应的累加系统机械能,为结构势能Es、结构动能Ek、颗粒群动能Dk、颗粒群惯容对应转动动能DR、颗粒群与结构之间的碰撞弹性势能Ds之和。 图12 结构体系能量变化规律Fig.12 Energy change rule of controlled system 由图12可知,前期颗粒运动较为剧烈,颗粒群与碰撞板的碰撞次数较多,因此前期颗粒群碰撞耗能较为充分,对应结构自身的总能量(Ev+Es+Ek)衰减较快。系统稳定后,EISM-CE对应的能量比Ev∶Dc=1∶1.85,EISM对应的能量比Ev∶De∶DRe= 1∶0.59∶0.5。总体来看,自由振动的能量耗散主要是以颗粒与结构的相互作用的方式进行耗散。另外需要注意的是,由于EISM-CE考虑了碰撞过程中的时间效应,碰撞初期EISM-CE耗能能力更加充分,因此能量趋于稳定的时间更短。 在共振激励下,进行NPPD减振性能分析,激励幅值取0.03g,基于数值仿真可得结构位移时程曲线如图13所示。由图13可知,简谐激励下NPPD具有较好的减振效果。系统稳定后EISM对应减振性能略优于EISM-CE对应减振性能,这一定程度上说明碰撞恢复系数相比较于接触单元耗能更加高效。时程曲线详细分析表明,由于EISM-CE对应碰撞间距较小,且采用接触单元法模拟碰撞过程中颗粒群与结构之间的相互作用,系统非线性相对较小,因此对应等效集中质量能够更快速地趋于稳定。相比之下,EISM对应等效集中质量趋于稳定较慢,且存在一定的分叉现象。 图13 简谐激励下位移时程曲线(ω=ωn)Fig.13 Displacement time history curve under harmonic excitation (ω=ωn) 简谐激励下系统能量累加曲线如图14所示。由图14可知,系统稳定后EISM-CE对应Ev∶Dc=1∶2.79,EISM对应的Ev∶De∶DRe=1∶1.64∶1.39。对于EISM-CE而言,系统能量主要通过c1耗散,而EISM主要是通过颗粒群与结构之间的垂直碰撞耗能和颗粒群转动引起的耗能所耗散。 图14 简谐激励下能量变化规律Fig.14 Energy change law under harmonic excitation 选取El-Centro地震动记录、Kobe地震动记录及Taft地震动记录作为振动台输入,并调整地震动记录峰值为0.20g,进行减震效果分析。El-Centro及Taft地震动记录作用下受控结构及原结构的位移时程曲线,如图15所示。不同力学模型减震效果特征值统计如表3所示。分析可知,NPPD对最大位移响应及均方根位移响应均具有一定的减震作用,其中RMS对应的减震效果优于最大位移对应的减震效果。这是在瞬态响应下,阻尼器无法充分发挥减振性能导致。其中,需要注意的是,由于Kobe地震动记录的频谱范围较宽,对其减震效果并不理想。不同模型对应减震效果分析结果表明,考虑碰撞时间效应后,EISM-CE对应减震效果略优于EISM模拟结果。 表3 地震作用下受控结构减振效果分析 图15 多颗粒阻尼器减震效果分析Fig.15 Damping effect analyses of M-PD El-Centro及Kobe地震动下系统能量累加曲线如图16和图17所示。由图16和图17可知:在振动初期,结构运动幅值较小,颗粒群运动并不充分,阻尼器的动能及势能较小,对应NPPD并未充分发挥其减震性能;随着结构响应的增加,颗粒运动剧烈程度逐渐增加,NPPD减震性能逐渐增加。与Kobe地震动记录相比,El-Centro及Taft地震动记录下结构的动能、势能稳定发展,颗粒与结构之间的阻尼耗能更加充分,对应减震效果更加明显。 图16 El-Centro地震动下系统能量累加曲线Fig.16 Energy accumulation curve of system under El-Centro input 图17 Kobe地震动下系统能量累加曲线Fig.17 Energy accumulation curve of system under Kobe input 地震作用下不同力学模型结构的自身耗能与对应阻尼器耗能占比如表4所示。表4中,Ein为外部输入能量。EISM-CE与EISM对应的Ein分别为E1和E2。分析结果表明,不同地震动记录下,EISM-CE模型对应系统能量主要通过颗粒群碰撞阻尼进行耗散。受地震动差异性影响,不同地震动记录下能量耗散占比有所区别,其中Kobe地震动记录下阻尼器耗能占比最大,Dc/Ev=2.42。不同力学模型对应耗能占比分析结果表明,与EISM-CE相比,EISM对应结构自身耗能占比总体高于阻尼器自身耗能占比。EISM对应减震机理与EISM-CE对应减震机理存在一定的差异性。在EISM作用下,颗粒碰撞一定程度上激起了结构响应,使得结构自身耗能占比提升。相比之下,EISM-CE主要通过颗粒群自身进行耗散。 表4 耗能成分对比Tab.4 Comparison of energy consumption 单位:% 在现有考虑惯容的等效单颗粒模型(EISM)研究基础上,本文提出了基于接触单元法的等效惯性单颗粒力学模型(EISM-CE)。试验及数值仿真分析结果表明,本文提出的EISM-CE同样能够较好地模拟NPPD减振性能,模型等效原则及物理参数取值原则是合理有效的。具体结论如下: (1) 简谐激励作用下,不同填充率对减振效果影响分析表明,当γ=30%时,颗粒与结构未发生充分碰撞,此时减振效果较弱;随着填充率的逐渐增加,减振效果呈现先增加后减小的趋势,当γ=90%时,减振效果最优;随着γ的进一步增加,虽然颗粒与容器壁的碰撞次数逐渐增加,但冲击力逐渐减小,颗粒群无法充分发挥耗能能力,致使NPPD减振效果降低。 (2) 与EISM相比,EISM-CE考虑了碰撞过程中的时间效应,位移放大系数频响曲线拟合更加光滑。简谐激励及地震作用下等效模型试验验证综合表明EISM-CE能够更加合理地反映NPPD的减振效果及机理。 (3) 减振性能数值分析结果表明,NPPD具有良好的减震效果。不同力学模型对比分析结果表明,由于力学模型的差异性,不同力学模型展示的NPPD的减振性能及机理存在一定的差异。在简谐激励下,系统稳定后EISM对应阻尼器耗能占比高于EISM-CE对应阻尼器耗能占比。相比之下,在自由振动及地震动作用下,EISM-CE对应阻尼器耗能占比高于EISM对应阻尼器耗能占比。需要注意的是,在地震动作用下,EISM-CE对应阻尼器耗能占比高于结构自身耗能占比,这与EISM存在一定差异。地震动作用下,碰撞时间效应的引入所展现的NPPD减震机理差异性更加明显。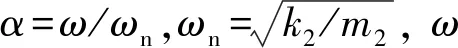
1.3 碰撞阶段体系的运动方程
2 等效力学模型的试验验证
2.1 试验设计

2.2 模型参数等效原则
2.3 简谐激励下等效模型试验验证
2.4 地震动作用下力学模型试验验证
3 基于等效模型的NPPD减振性能分析
3.1 自由振动
3.2 简谐激励
3.3 地震动作用
4 结 论

