内凹-星型三维负泊松比结构设计及冲击吸能特性

王玮婧, 张伟明, 郭孟甫, 杨金水, 马 力

(1. 哈尔滨工程大学 青岛创新发展基地,山东 青岛 266000;2. 哈尔滨工业大学 复合材料与结构研究所,哈尔滨 150001;3. 北京航天发射技术研究所,北京 100076)

随着科学技术的不断进步和发展,人们不再满足于追求和探索具有高性能的常规材料。具有多种优异性能的轻量化反常规材料(或结构)成为了结构设计师们探索的新目标。负泊松比结构作为轻质多孔结构中特殊的一类,不仅具有多孔结构的一般性能,因其独特的变形机制还兼具了许多其他的优异性能,如优异的断裂韧性[1]、压痕阻性[2]、较高的剪切模量[3]、良好的减振性能[4-5]、隔声性能[6]、曲率同向性、渗透率可变性、能量吸收性能等。

胞元结构设计是改变结构负泊松比效应的主要途径。近年来,针对具有负泊松比效应的新结构设计不断涌现,包括星形-四边形结构[7]、十字截头体结构[8]、八边形蜂窝结构[9]、钢丝编织Kagome结构[10]等,如图1所示。这些新构型的提出极大程度地丰富了负泊松比机械超材料的发展和应用。

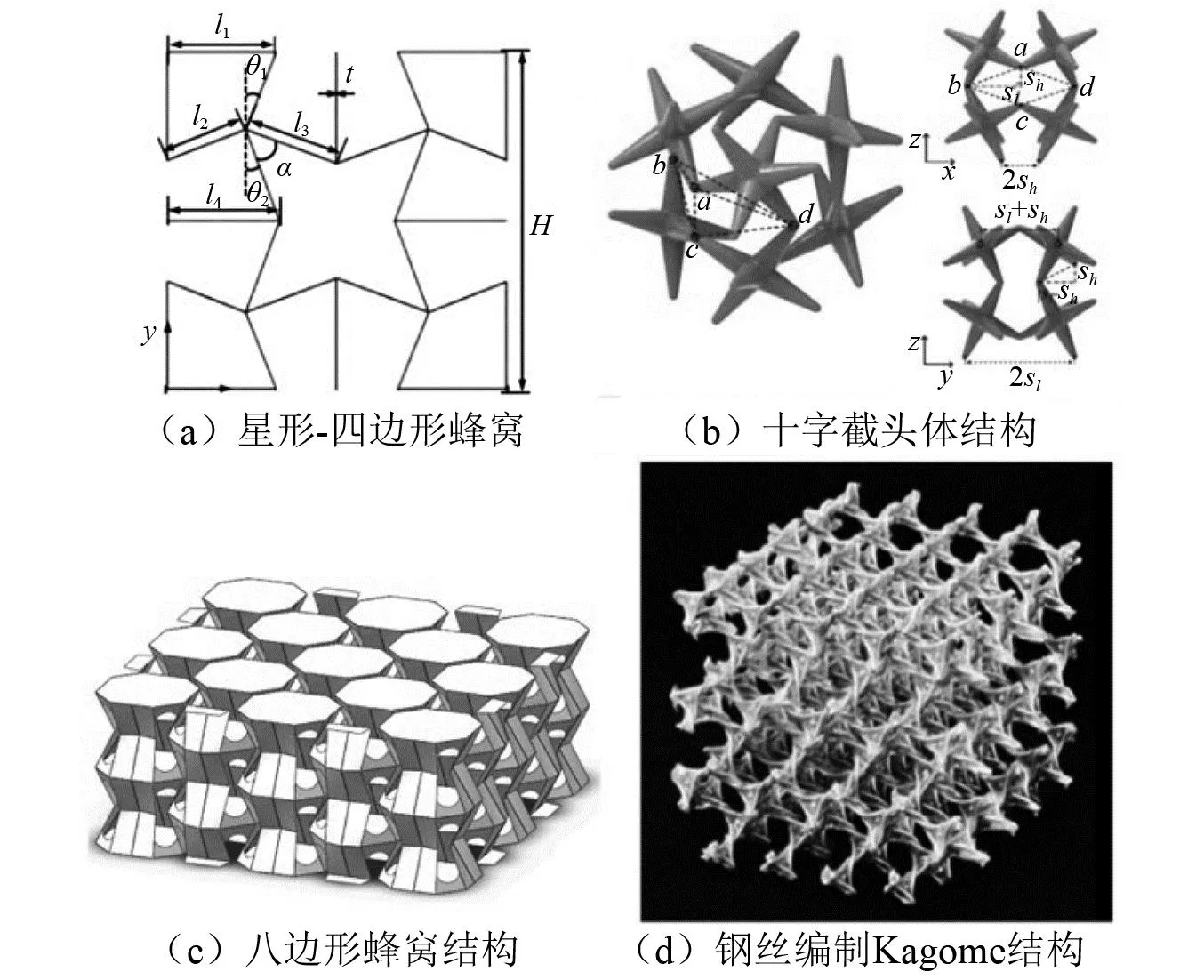
图1 负泊松比结构Fig.1 Negative Poisson’s ratio structure

与结构较为复杂的新构型相比,具有负泊松比效应的传统构型由于提出更早、构型更加简单而受到广大学者的青睐,因此对于传统负泊松比结构力学性能的研究更加深入和全面。对于内凹六边形蜂窝结构,Gibson等[11]推导了结构沿加载方向上的泊松比和弹性模量。Hu等[12]通过理论分析和数值模拟研究了胞元内凹角度和胞壁长度对内凹形负泊松比结构大变形下的单轴动态冲击性能的影响,并对冲击过程中平均冲击应力的经验公式进行了推导。对于内凹星形结构,Theocaris等[13]对不同星形角度下蜂窝结构的弹性常数进行了表征。黄泽彬等[14]基于能量法给出了星形蜂窝结构在弹性变形范围内面内等效力学性能的理论计算模型。

由于负泊松比结构在缓冲吸能方面的优异表现,许多学者也对其吸能性能进行了研究。崔世堂等[15]讨论了冲击速度对内凹形蜂窝结构面内冲击模式和能量吸收能力的影响。魏路路等[16]在内凹六边形蜂窝和手性蜂窝的基础上,提出了一种内凹-反手性结构并对其吸能性能进行了表征。其结果表明:与三边反手性蜂窝及传统蜂窝相比,内凹-反手性蜂窝的能量吸收性能更强。在已有的冲击载荷下蜂窝结构平台应力理论模型的基础上,白临奇等[17]建立了箭头型蜂窝结构受冲击载荷时吸收能量的理论模型,得到了其在冲击载荷下不同阶段吸收能量及对应等效应力大小与几何参数的关系。杨泽水等[18]研究了不同角度下的三维星形负泊松比结构的吸能特性。马芳武等[19]研究了不同内凹边数和内凹角度的内凹三角形蜂窝结构在不同冲击速度下的吸能行为。

从现有的研究成果来看,对于负泊松比结构的研究主要集中在二维结构,现有的三维结构也大多来源于已有的二维传统结构,对于增益负泊松结构吸能性能的新构型设计较少。基于以上不足,本文提出了一种新型负泊松比结构,在之前的工作中,对于二维结构已经进行了系统的研究[20-21]。本文将在此基础上,对三维新型负泊松比结构的力学性能以及动态吸能性能进行研究。

1 结构设计与表征

1.1 几何关系

现有的研究成果表明,内凹六边形蜂窝和星形蜂窝都是具有良好吸能性能的负泊松比轻质多孔结构。基于此,本文提出了内凹-星型结构,其二维胞元结构如图2所示。对二维结构进行正交旋转即可得到三维内凹-星型结构,如图3所示。

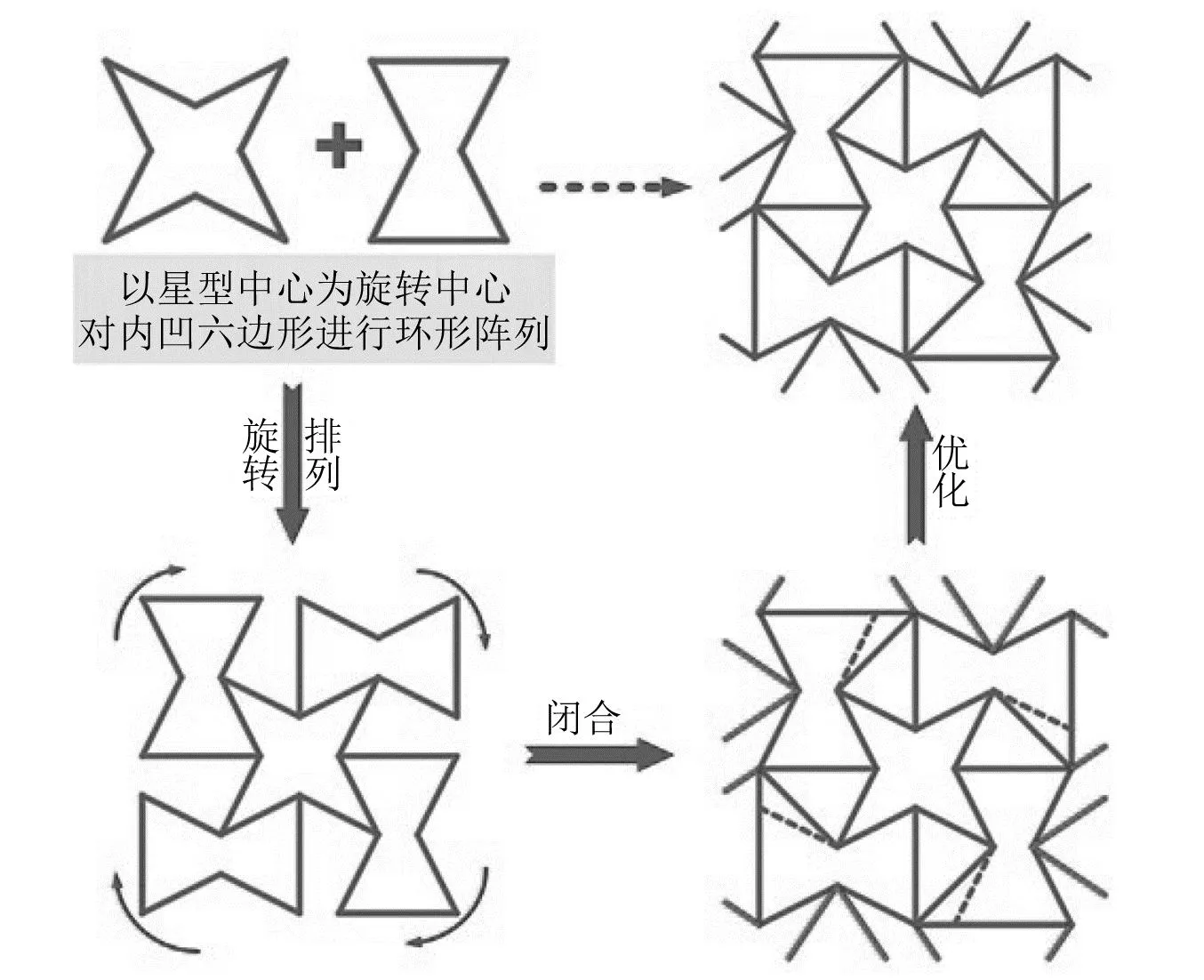
图2 内凹-星型负泊松比结构(二维)Fig.2 Concave-star negative Poisson’s ratio structure (2D)

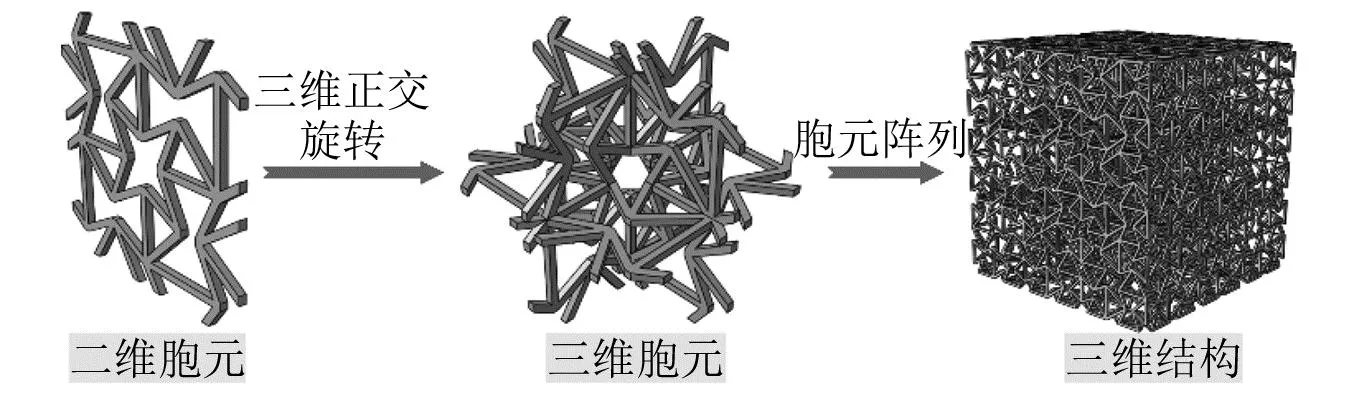
图3 内凹-星型负泊松比结构(三维)Fig.3 Concave-star negative Poisson’s ratio structure (3D)

内凹-星型蜂窝具备参数可调控性,具有基本的几何参数(凹角参数λ和壁厚参数γ)以及两个特征边长H和K,其几何关系如图4所示,关系方程如式(1)～式(4)所示。考虑到内凹-星型蜂窝因参数不同而具备不同的几何形态及胞元结构,本文将统一以Nij(i/j为R1/R2的相对比值,当R1=0时,定义i=0,j=1)命名内凹-星型蜂窝。

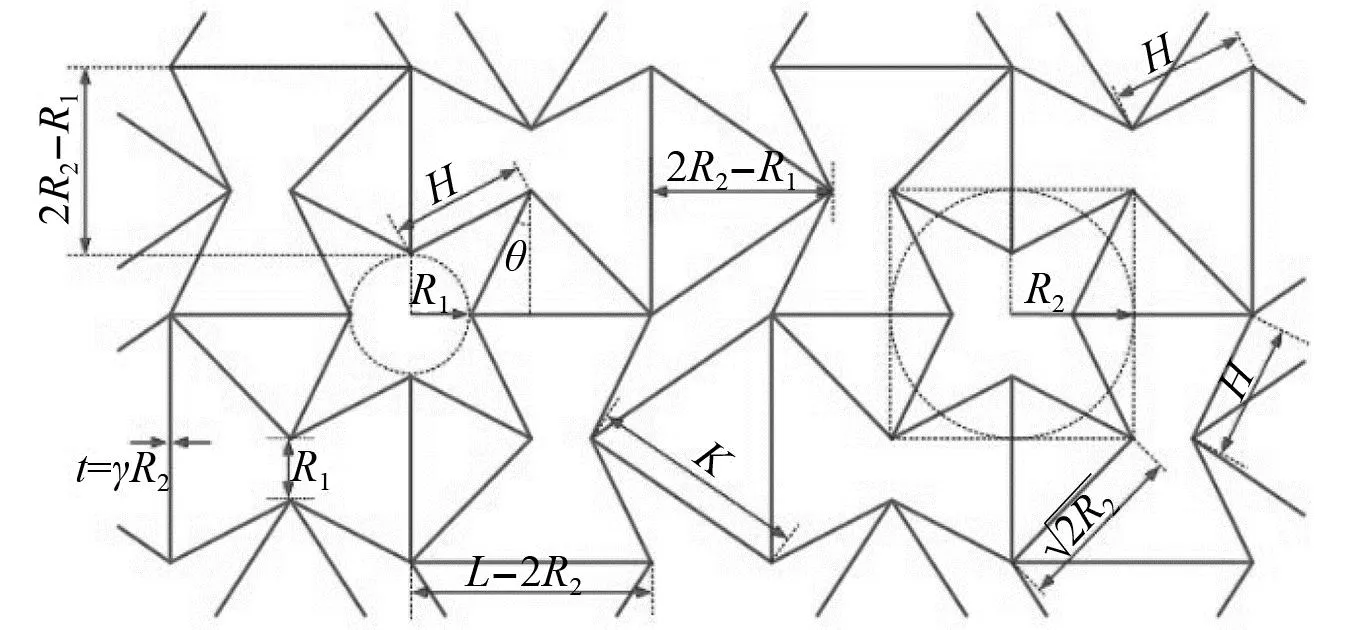
图4 内凹-星型蜂窝几何表征Fig.4 Geometric characterization of concave-star honeycomb

(1)

(2)

(3)

(4)

由几何关系,可以得到单胞x方向长度为

Lc=5R2=2.5L

(5)

根据正交排列特点,可以进一步得到,胞元尺寸为

Vc=5R2×5R2×5R2

(6)

1.2 密实应变

相对密度是结构轻量化设计的重要参考指标,正确表征其与几何参数之间的关系是十分重要的。相对密度被定义为结构密度ρ*与材料密度ρs的比值。经推导,三维内凹-星型蜂窝结构的相对密度可由如下关系表达

(7)

其中,需要注意的是,当λ=0时,胞元中星形部分的每一条边都与对称中心紧密相连,最初带有凹角间隙的位置被一个稳定的三角形所取代。新胞元结构在λ≠0时的连接方式如图5(a)所示。当λ=0时,式(7)的连接方法是在中心进行分离如图5(b)所示,而实际中其连接方法是中心与边不分离,如图5(c)所示。因此,式(7)的理论不适用于λ=0的情况,在λ=0时,其相对密度遵循如下表达式

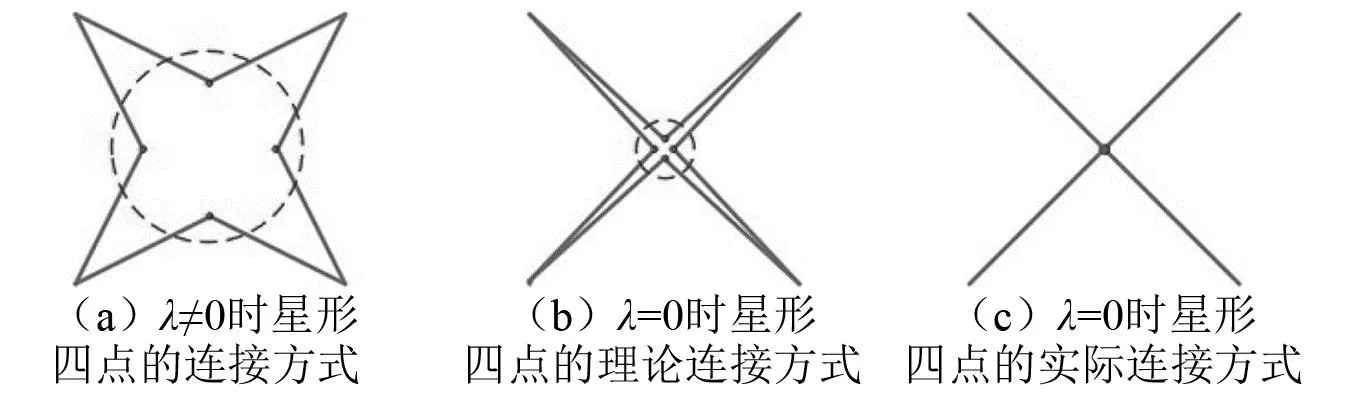
图5 星形连接方式Fig.5 Star connection mode

(8)

密实应变是一个与胞元结构以及结构的吸能量密切相关的参数。理论上,致密应变等于孔隙率,即1-ρr。但在试验中发现,密实应变小于孔隙率。因此致密应变可以用经验系数的表达式计算

(9)

当λ=0时,则有

(10)

式中,η为影响因子,取决于胞元结构,其取值范围为1～3。对于蜂窝结构,Gibson等建议η=1.4。值得注意的是,本文仅在结果比较部分时采用了η=1.4的取值。由于η的值不影响密实应变与相对密度之间的线性关系,因此在理论分析的其他部分中,η仅作为一个变参量在表达式中给出,没有赋予一个特定的值。

1.3 弹性常数

弹性常数主要包括弹性模量、泊松比和剪切模量。对于三维内凹-星型蜂窝结构,由于其排列方式的特殊性导致其表现为各向同性,因此,对于三维内凹-星型蜂窝结构的理论分析可以简化到二维,建立的分析模型如图6所示。

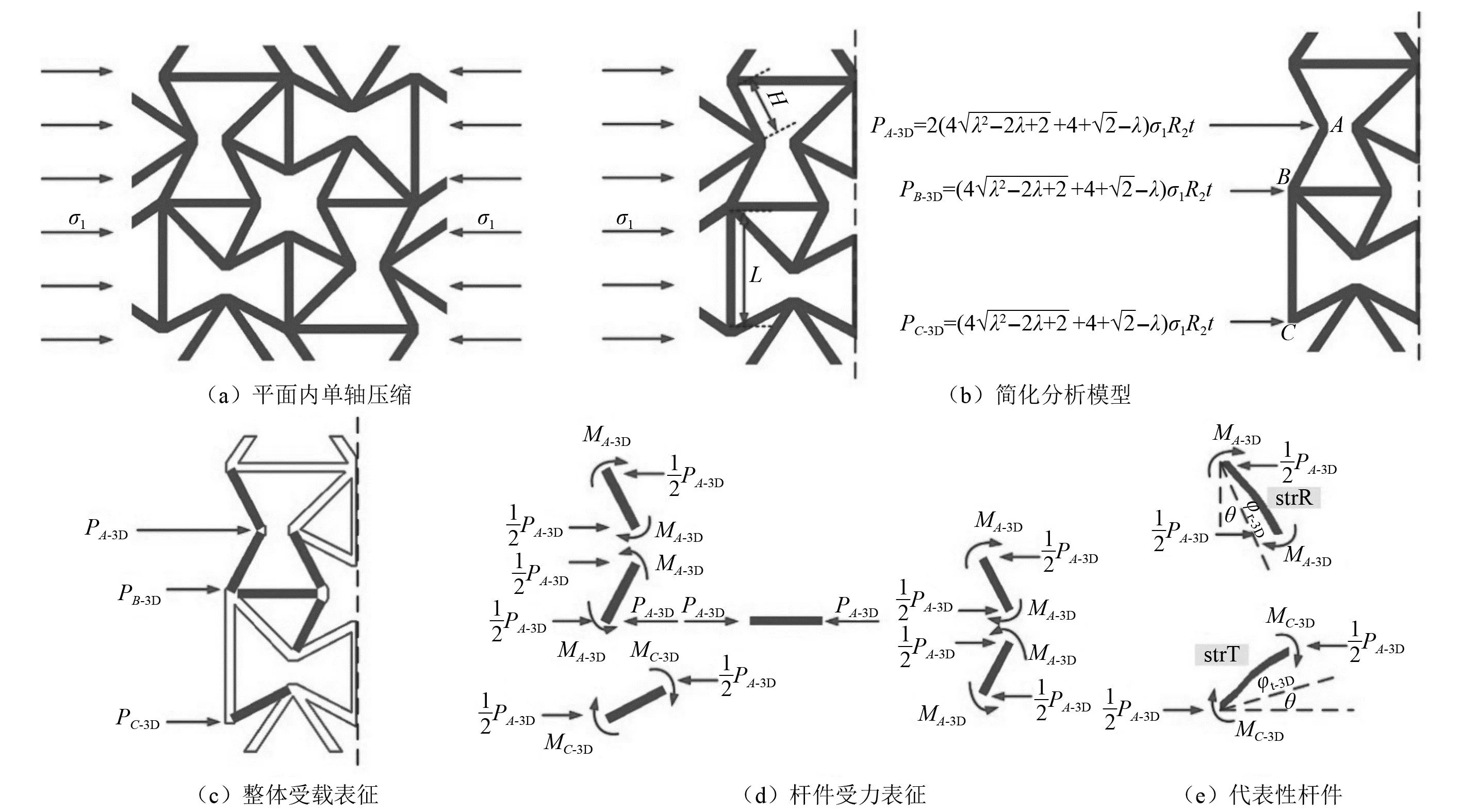
图6 三维内凹-星型负泊松比结构理论模型Fig.6 Theoretical model of three-dimensional concave-star negative Poisson’s ratio structure

由图6给出的分析模型可以看出,整个胞元结构的位移变化可以通过两个代表性杆件strR和strT(已在图6(e)中标出)求得。反作用力PA-3D、PB-3D、PC-3D分别作用于A、B、C三点,其大小和方向可以根据胞元结构在X方向受力平衡得出

(11)

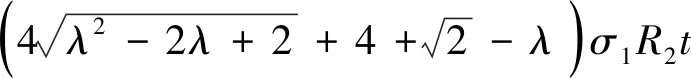
(12)

在单轴压缩作用下,具有代表性的杆件strR和strT在加载过程中会发生XY平面内的弯曲变形。弯曲力矩可以根据力矩平衡给出

(13)

(14)

则代表性杆件的挠度可由力法给出

(15)

(16)

其中,

(17)

(18)

式中:Es为结构母材的弹性模量;I为截面惯性矩。

(19)

(20)

胞元在X和Y方向上的应变可以通过代表性杆件strR和strT的挠度来获得

(21)

(22)

因此,X方向的弹性模量可表示为

(23)

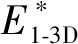
XY平面内的泊松比和剪切模量可以表示为

(24)

(25)

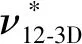
值得注意的是,当λ=0时,结构全部由稳定的三角形构成,上述的分析结果不再适用,在之前的工作中,已经给出了二维N01构型的理论计算方法[22],由于三维内凹-星型蜂窝结构正交排列的特殊性,其弹性常数可以通过二维构型的计算结果乘以面积比来近似表达

(26)

(27)

式中:n为三维结构中纵向正交插板的个数;Lz为结构总长。依此,可以得到三维N01构型的剪切模量的表达式

发酵液中ACE抑制活性测定采用高效液相色谱法，其检测条件：C18色谱柱(4.6 mm×250 mm)；检测波长228 nm；柱温20 ℃；流动相：水∶甲醇为40∶60(均含0.1%甲酸，V/V)；流速0.8 mL/min；进样量10 μL。

(28)

2 数值模拟

有限元分析在商用有限元软件ABAQUS中进行。由于内凹-星型蜂窝结构的参数可调控性,本文选取了四种具有代表性的结构来进行有限元模拟,如图7所示。在模拟过程中,结构模型将被放置在两个刚性圆盘之间,刚性圆盘直径为170 mm,质量8 kg。为防止模型单元与圆盘单元重合,结构模型与上、下刚性圆盘之间将留有1 mm的微小间距,如图8所示。结构母材选用热塑性聚氨酯弹性体橡胶(thermoplastic polyurethanes, TPU),其材料参数如表1所示。为防止加载过程中出现穿透,有限元模型被设置为通用接触,其中法向行为设置为“硬”接触,其作用是防止接触对之间出现穿透行为。切向行为设置为“罚”接触,表达了切向摩擦力,摩擦因数为0.2。不同加载条件的模拟通过在上刚性圆盘施加不同的位移载荷实现。

表1 TPU力学性能参数Tab.1 Mechanical properties parameters of TPU

图8 有限元模型Fig.8 Finite element model

为了评价内凹-星型蜂窝结构的吸能能力,本文选用了两种传统蜂窝结构(内凹型蜂窝和星形蜂窝)来进行比较。其中,WSH蜂窝的胞元个数为27(3×3×3),R2=6.4 mm,胞壁厚度t=1 mm,γ=0.156 25,整体尺寸为97 mm×97 mm×97 mm,有限元模型见图7。在模拟过程中选择矩形截面梁单元来进行简化,以保证计算速度。网格收敛性分析如图9所示,当整体网格尺寸为1 mm时,计算结果收敛,为保证计算精度,用于本文的有限元模拟的网格整体尺寸为0.5 mm。

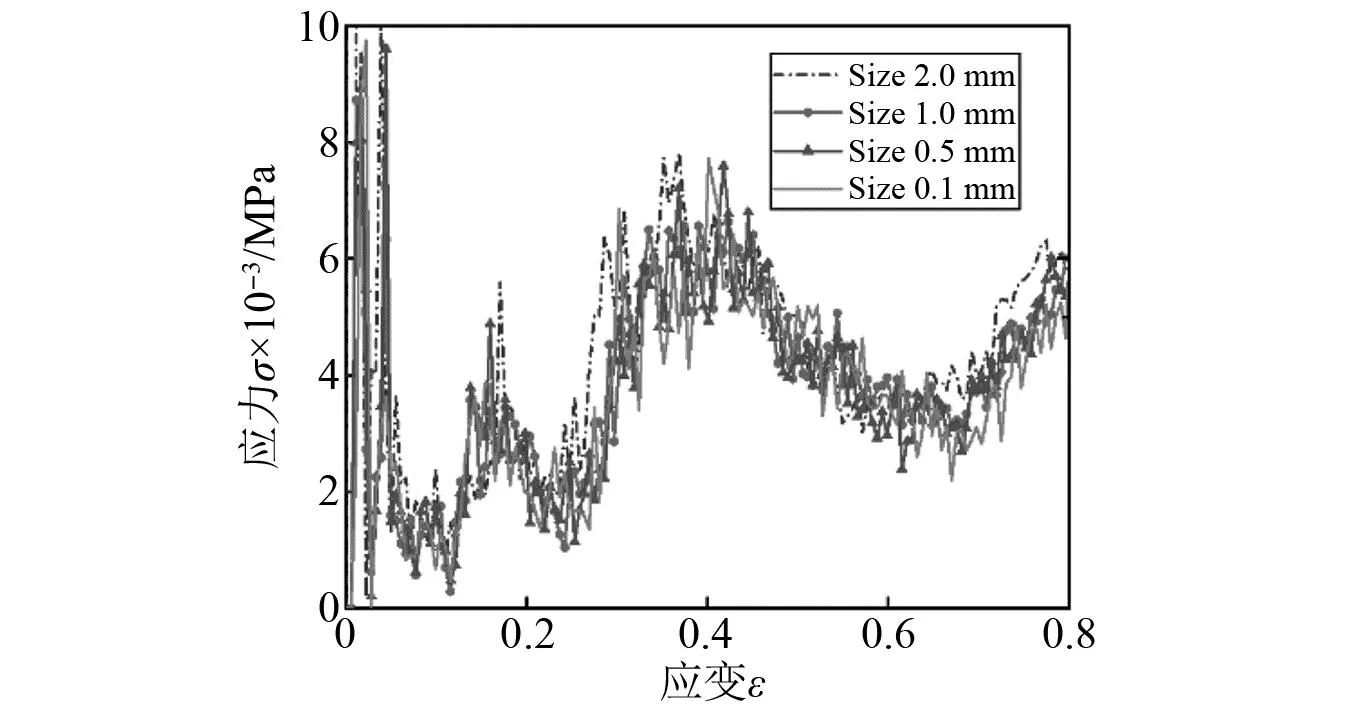
图9 网格收敛性分析Fig.9 Convergence analysis

为了研究三维内凹-星型蜂窝的静态力学性能,进行了准静态轴向压缩模拟。压缩过程通过在上压盘施加恒定速度实现。为了研究三维内凹-星型蜂窝的动态力学性能,在ABAQUS/Explicit模块进行了恒速平面压缩模拟。通常情况下,依据变形模式,可以将速度划分为低速、中速和高速三个区间。在之前的工作中,也对两种临界速度进行了理论求解,其表达式如下

(29)

式中:Vcr1为第一临界速度,即低、中速的临界速度;εcr为结构达到初始峰值应力时的应变。

(30)

式中:Vcr2为第二临界速度,即中、高速的临界速度;σR为静态压缩条件下结构的平台应力值。

依据两种临界速度的计算公式,结合静态仿真模拟的结果,可以计算出适用于该模型的临界速度。其具体结果为:Vcr1=1.2 m/s,Vcr2=4.32 m/s。基于计算出的临界速度,本文将以1 m/s、3 m/s、6 m/s分别作为低、中、高速的代表性速度来进行有限元分析。

3 结果与讨论

3.1 变参量分析

为了更加直观地描述不同几何参数下结构的几何特性和力学性能,根据第1章的分析结果,几何参数(凹角参数λ和厚度参数γ)与相对密度、密实应变、弹性模量以及泊松比的关系,如图10所示。

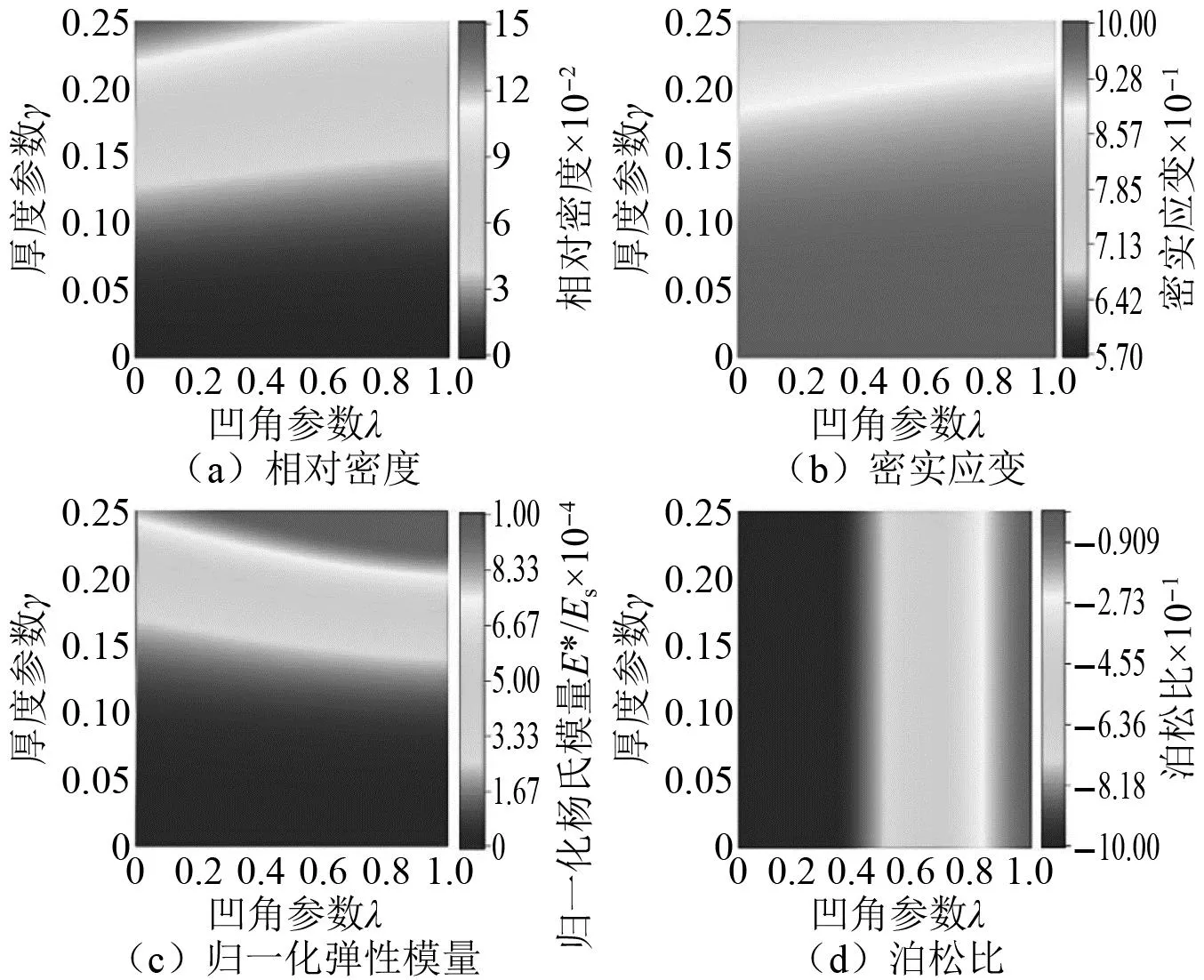
图10 几何参数与性能参数的关系Fig.10 Relationship between geometric parameters and performance parameters

图10中清晰地给出了随着几何参数改变结构性能的变化情况。具体表现为:当凹角参数相同时,随着厚度参数的增加结构的相对密度增加、密实化应变减小,结构刚度增加,符合普遍规律。此外,在密实化应变云图中,当厚度参数小于0.15时,在全凹角参数域内,密实化应变接近1,这意味着结构具有更长的平台应力。图10(c)～图10(d)给出了WSH蜂窝结构几何参数与力学性能的关系,理论上全参数域内结构为非正泊松比。

3.2 准静态压缩性能

为了验证理论推导的正确性以及数值模拟的合理性,准静态压缩条件下N12-3D在线弹性阶段泊松比和弹性模量的理论与仿真值对比,如图11所示。在泊松比图中,理论和仿真值具有很好的一致性。其中N12构型和N23构型具有负泊松比值,表现出良好的负泊松比特性。理论和仿真值的差距主要由边界效应引起。理论模型计算过程中,假设胞元数量足够多,从而忽略了边界效应的影响。在弹性模量对比图中,理论值略高于仿真值,这是因为选用梁单元低估了结构的刚度所致。但从总体来看,理论值和仿真值具有良好的一致性,验证了理论的正确性以及仿真的可靠性。

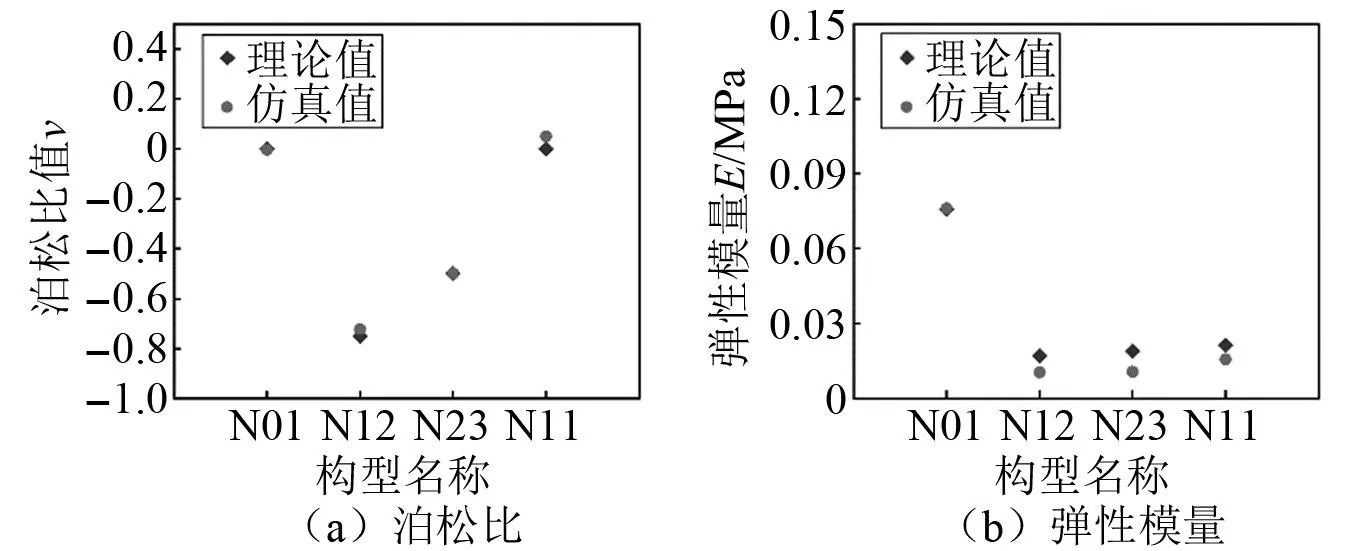
图11 N12-3D准静态压缩时线弹性阶段的弹性常数Fig.11 Elastic constants of linear elastic stage of N12-3D under quasi-static compression

准静态压缩模拟获取到的力学响应结果如图12所示。由图12可知,三维内凹-星型蜂窝结构的力学响应曲线满足负泊松比结构力学性能曲线的一般规律,即具有明显的线弹性阶段、平台阶段以及密实阶段。在线弹性阶段,构型N01相比其他构型具有更高的刚度,这与理论预测结果相符。此外,四种新构型相比两种传统构型都具有更高的刚度,这说明新构型的设计相比传统蜂窝增加了结构的面内刚度。在平台阶段,各结构具有不同的平台应力值,但都高于传统蜂窝结构的平台应力值。平台应力是评价结构吸能能力的一个重要指标,一般情况下,平台应力值越高代表其吸收能量越多。但受到密实化应变和结构相对密度的影响,该指标只是一个初步评价吸能水平的手段,更准确的评估应采用比吸能(即单位质量下结构吸收的能量),将在吸能部分进行详细讨论。在密实化阶段,可以注意到,N01的密实化应变值最小,这是因为其相对密度最大。

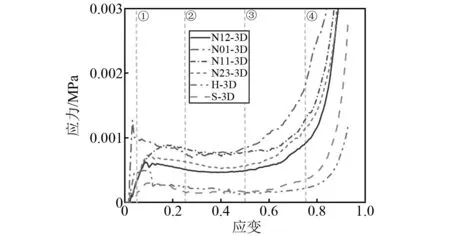
图12 准静态压缩时的力学响应曲线Fig.12 Mechanical response curve under quasi-static compression

N12-3D在准静态压缩状态下不同应变时的横向变形云图,如图13所示。由图13可知,随着纵向压缩其横向发生收缩变形,表现出负泊松比特性。值得注意的是,在应变为0.25时,结构出现局部失稳,但随着应变的增加,这种失稳现象并没有带来横向变形的变异,这与二维结构的结果不同。在二维结构中,结构的局部失稳导致整体倾斜,使结构在大变形阶段不再保持负泊松比特性。但在三维结构中,更大的变形空间以及更大的孔隙率,使得结构局部的失稳并未给结构负泊松比特性带来较大的影响。

图13 准静态压缩时N12-3D的横向变形云图Fig.13 The transverse deformation of N12-3D under quasi-static compression

3.2 恒速平压性能

恒速平压模拟是评价结构吸能能力的重要手段之一。N12-3D在不同速度时的数值模拟的名义应力-应变曲线,如图14(a)所示。

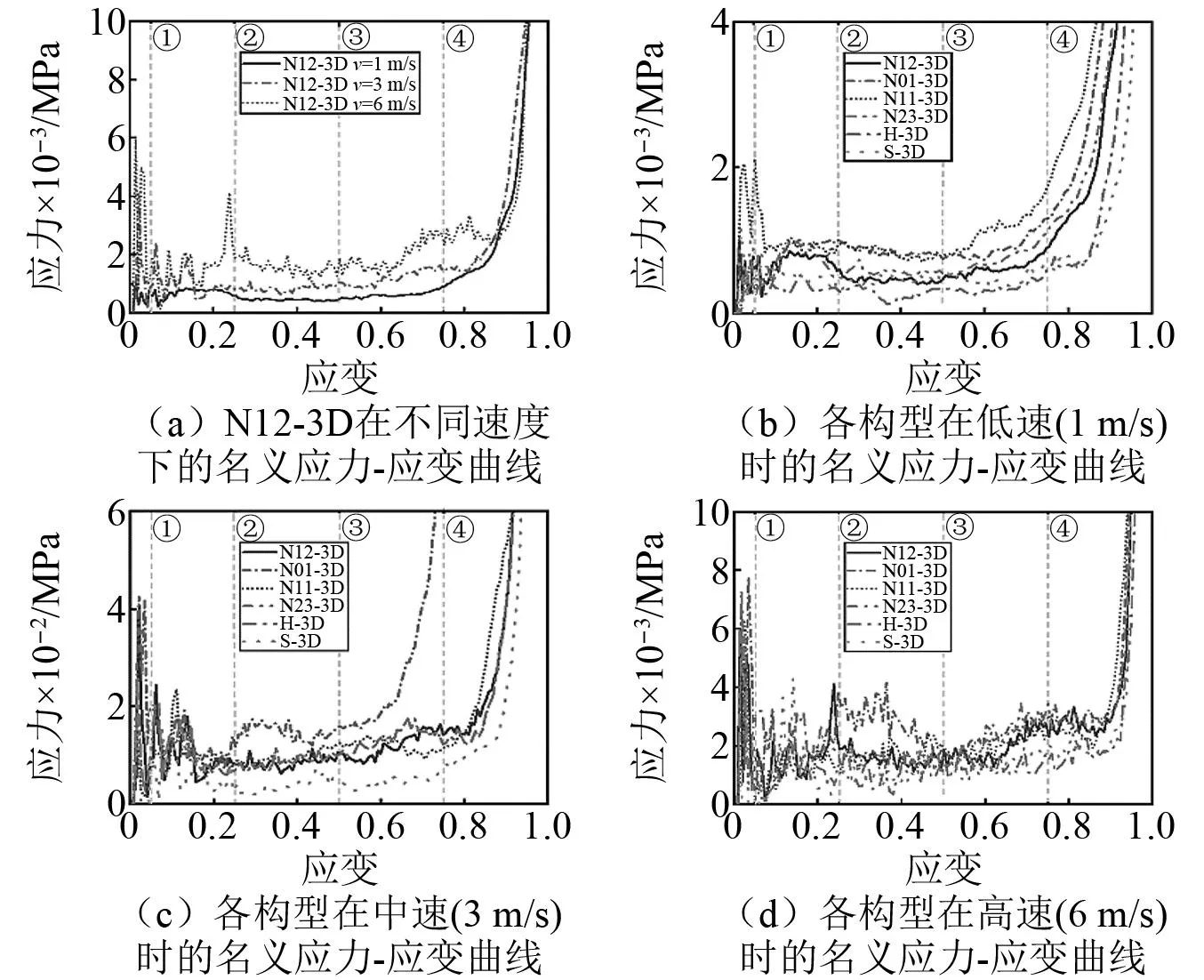
图14 各结构在低、中、高速下的动态力学响应Fig.14 Dynamic mechanical response of each structure under low, medium and high velocity

由图14(a)可知,它符合恒速平压的一般规律,即随着速度的增加,初始峰值应力和平台应力增加。图14(b)～图14(d)分别给出了各结构在低、中、高速的动态响应曲线。从图中可以得到:构型N01和构型N11具有几乎相同的平台应力值,但N11构型的峰值应力显著低于N01构型的峰值应力,是理想的吸能构型。另外,随着速度的增加,各结构间平台应力的差异逐渐减小,这是因为随着速度的增加,结构设计带来的影响被弱化,各结构间的由于结构设计引起的差异减小,而更多取决于结构母材的性能。

为了更加直观地说明这个现象,低、中、高速时N12-3D结构的横向变形云图,如图15所示。低速时,结构呈现出明显的整体变形趋势,即随着应变的增加,结构整体发生变形,在小变形阶段具有明显的负泊松比效应,大变形阶段保持几乎整体近零泊松比的特性。当速度达到中速时,结构由整体变形过渡为局部变形模式,在全应变下保持负泊松比特性。当速度为高速时,结构呈现自冲击端到固定端逐层压溃的变形模式,仍在全应变下保持负泊松比特性。在各速度区间,N12-3D的变形特征与理论计算得到的速度分区相吻合,验证了理论推导的正确性以及动态模拟的可靠性。

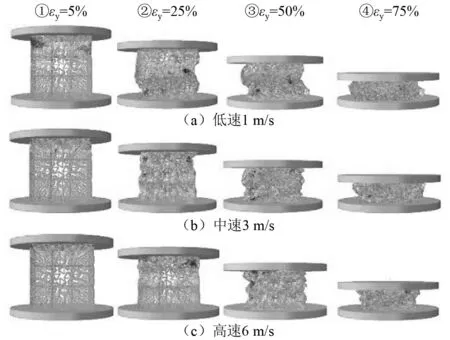
图15 不同速度下N12-3D的横向变形云图Fig.15 Transverse deformation of N12-3D at different velocities

此外,值得注意的是,在现有的结构中,大部分结构不具备负泊松比稳定性,即大变形下很难维持负泊松比特性。但内凹-星型蜂窝的设计为保持大变形负泊松比特性提供了设计方案。在纵向压缩应变为0.75时,N12-3D仍保持横向收缩,具有明显的负泊松比变形,见图13(b)和图13(c)。

3.3 内凹-星型蜂窝结构能量吸收性能

比吸能是评价结构吸能性能的一个重要指标。比吸能的计算表达式如下

(31)

式中:ν*为结构体积;m为结构质量;Esea为单位质量的能量吸收量。

依据比吸能的计算公式,各结构在不同速度下的比吸能曲线,如图16所示。

由图16可知,准静态压缩条件下,三维内凹-星型蜂窝的各构型相比于两种传统蜂窝具有更高的比吸能值,即三维内凹-星型蜂窝表现出优于传统蜂窝的吸能能力。其中,构型N01和构型N11的比吸能值相当。构型N01由稳定的三角形组成,其刚度最高,在负泊松比结构普遍较软的情况下,高刚度的负泊松比结构具有可观的应用价值。而构型N11十分简洁,其中心结构为正方形结构,孔隙率高,相对密度低,能够满足轻量化需求。值得注意的是,虽然构型N11的刚度相比N01较弱,但其仍高于传统星形蜂窝,与传统内凹型蜂窝刚度相当,但吸能能力远高于传统内凹型蜂窝结构。

在低速时,构型N01和构型N11仍表现出十分优异的吸能能力,N12-3D和N23-3D的吸能能力稍弱于传统内凹型蜂窝,但远高于星型蜂窝结构。当速度达到中速时,构型N01的吸能能力与传统内凹型蜂窝结构相当,但其刚度远高于传统内凹型蜂窝,仍是更为理想的负泊松比材料。其他三种新型内凹-星型蜂窝结构其吸能性能虽不如传统内凹型蜂窝但远高于传统星型蜂窝结构,是较为理想的吸能材料。当速度达到高速时,构型N01的比吸能值略高于传统内凹型蜂窝结构,其他构型略低于传统内凹型蜂窝结构而远高于传统星型蜂窝结构,为三维吸能材料设计提供了设计思路。

综合来看,三维内凹-星型蜂窝结构在静态条件下吸能表现最优,在应变为0.7时,最优构型N11-3D的比吸能值是传统内凹型蜂窝结构的2.64倍,是传统星型蜂窝结构的3.89倍。

在动态冲击条件下,三维内凹-星型蜂窝结构与内凹型蜂窝相比在中高速时吸能优势不大,但其更高刚度以及良好的零/负泊松比特性仍使其在工程实际应用中更具优势,是理想的吸能结构。

4 结 论

本文设计并表征了一种参数可调的具有优异吸能性能的轻质三维内凹-星型蜂窝负泊松比结构。并通过理论和数值模拟相结合的研究方法系统地研究了新型三维内凹-星型蜂窝的静/动态力学响应以及吸能特性,得到了一些结论,总结如下:

(1) 本文通过理论研究给出了结构相对密度的表达式,基于力法推导了三维内凹-星型蜂窝的弹性常数(面内泊松比、弹性模量和剪切模量)的表达式,给出了使结构变形模式发生改变的两种临界速度的理论预报公式,并通过数值模拟验证了理论推导的正确性。

(2) 通过数值模拟和理论预报相结合的研究手段分析了三维新型蜂窝的静态力学行为。研究发现:三维新型内凹-星型蜂窝结构相比两种传统蜂窝结构具有更高的面内刚度和更好的吸能性能。以N11-3D为例,在应变0.7时,其比吸能值是传统内凹型蜂窝结构的2.64倍,是传统星型蜂窝结构的3.89倍。

(3) 基于数值模拟的研究方法分析了三维内凹-星型蜂窝的动态力学行为。研究结果表明,三维内凹-星型蜂窝结构在低、中、高速全域内的吸能性能均远高于传统星形蜂窝结构。在中高速时,三维内凹-星型蜂窝结构的吸能能力与内凹型蜂窝相当,但其更高的面内刚度以及更好的零/负泊松比特性仍使其在实际应用中更具优势。